『チ。-観測衛星ビジネス要素シミュレーション:衛星の軌道と撮像最大待ち時間について-』
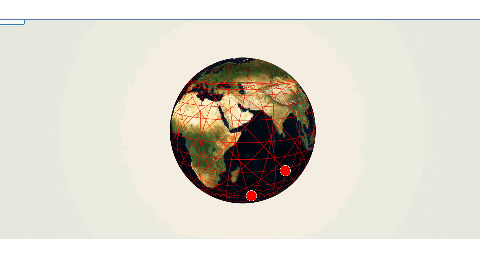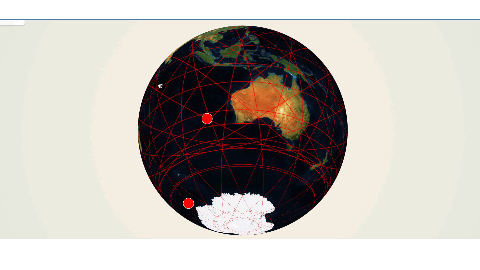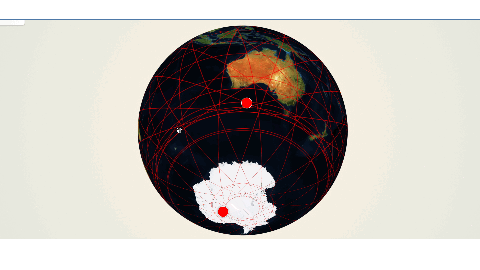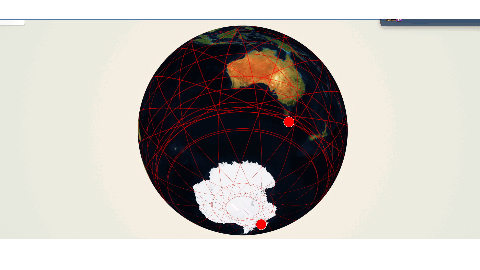
地球観測衛星のビジネスモデルと軌道
衛星ビジネスにおいて、特定の地域(AOI:AreaOfInterest)をどのくらいの頻度で撮像できるのかということはビジネスの価値に直結しています。 そしてどの地域をどのくらいの頻度で取れるかは、打ち上げ後の軌道投入地点、傾斜角度、高度できまってきます。 そして、ここが面白いところなのですが高度が決まると衛星の速度が決まり、1日に何回地球を回ることができるのかも決まるのです。
質問:衛星の高度が上がると衛星の速度は上がる? Yes?No?
正解:Noです。 実は高度が低いほうが衛星は早く回っているのです。
低軌道衛星という地上500-700km に打ち上げている衛星は地球を1日に14-16周回っています。
一方で静止衛星(気象衛星や衛星放送)が上がっているのは地上36000km です。 上空でとまっているように見えるのでパラボラアンテナが固定できるのですが、それは地球と同じスピード1日に地球を1周まわっているからです。
実は衛星1機では撮りたい地域はすぐ取れない
わたしも宇宙ビジネスにかかわるまではそうだったのですが、一般人のイメージで、衛星はすきなところにいくように操作できると考えている人も多いと思います。はやぶさのように惑星探査目的の衛星であれば制御方法も多様ですが、 最近の低軌道小型衛星は ほとんど最初にロケットから放出されたときの運動エネルギーの慣性で地球上空を回り続けているだけです。 実際には何も制御しないと地球の重力で少しづつ落下していくので、スラスターで高度を上げるといった機能がついている程度です。
なので、放出されるときの傾斜角度と、高度と、地点が非常に重要でそれによってどの地点をどのくらいの頻度でとれるのかということが決まります。
そして、衛星から撮像できる地点というのは衛星の直下から半径数百キロ程度と意外と少ないのです。
なので、複数の衛星を打ち上げて、ある地点を取れる頻度を向上させようという考えに当然なっていきます。
この複数衛星で一つのサービスを提供することを衛星コンステレーションといいます。
コンステレーションとは星座という意味です。ロマンチックな言い方ですね。
2Dと3Dを切り替えて、地球を回して理解する、sun-synchronous Orbit(太陽同期軌道)と、inclined Orbit(傾斜軌道)
さて、地球観測衛星を打ち上げる軌道は大きく分けて以下の2種類に分けられます。
- sun-synchronous(太陽同期軌道)
- 衛星は1日に1回、ある場所を同じ太陽の下(同じ現地時刻)で通過します。つまり、例えば毎日午前10時に同じ地域を観測できるので、撮影条件が毎回ほぼ同じになります。
- この軌道は、ほぼ極軌道(地球の両極を通る軌道)に近く、地球の自転と組み合わせて、衛星の軌道面が太陽の方向に合わせてゆっくりずれていく仕組みになっています。
- 太陽同期軌道上の衛星は、実際には昼側と夜側の両方を通るため、光学衛星の場合は撮影できるのは、昼側の場合に限られます。SAR衛星の場合は両側で撮像できます。
- incliend orbit(傾斜軌道)
- 地球の赤道に対して斜めに傾いた軌道です。
- 太陽同期軌道ほどの厳しい条件はなく、ユーザーが自由に高度や傾斜角を決められます。
- そのため、毎日同じ現地時刻に通過する保証はなく、観測条件は変わる可能性があります.
これ、言葉だけで理解するのはかなり難しいですよね。
また、2次元の地図上に軌道の線を描画することがよくあるのですが
これも正直なんでそのような曲線になるのか納得感が薄いです。
本当は2D,3Dを切り替えてぐりぐり地球を動かして軌道を理解したい!
どの角度で衛星を飛ばせば、どこをどんなふうに飛んでいくのかシミュレーションしたい!
ということでVue+MapBoxでシミュレータ作ってみようと思います。
衛星の軌道をシミュレーションのために必要なこと
衛星の軌道情報構造(ユーザーが入力する)
基本要素はユーザーが入力できるようにします。
SimulationComponent
export const ORBIT_TYPES = {
SUN_SYNCHRONOUS: "sun-synchronous",
INCLINED: "inclined",
} as const;
interface SatelliteInput {
orbitType: OrbitType;
launchAngle: number; // 傾斜軌道の場合のみ有効(deg)
launchLat: number;
launchLon: number;
altitude: number; // [km]
meanMotion: number | null; // revs per day
}
そして、sun-synchronous の場合は太陽と同期する都合上、高度により傾斜角度がきまってきますのでそれを計算で出力するようにしておきます。(厳密性は今の時点では必要ないので円軌道で近似します)
低軌道(500-800)の場合は傾斜角97-98(赤道から真東を0度として北極方向が90度、つまり太陽の動きにあわせていく都合上少し西よりに飛んでいく)となります。
const J2 = 1.08262668e-3;
// 太陽同期軌道に必要な昇交点回帰率(rad/s)
// 1年 = 365.2422日 → 365.2422 * 86400秒
const dOmegadt_required = (-2 * Math.PI) / (365.2422 * 86400); // 約 -1.99e-7 rad/s
/**
* 与えられた高度 (km) に対して必要な太陽同期軌道の傾斜角(deg)を計算する関数
* 円軌道 (ecc=0) を仮定
*/
const calculateSunSyncInclination = (altitude: number): number => {
// 軌道半径
const a = R_EARTH + altitude; // km
// 平均運動 (rad/s)
const n = Math.sqrt(MU / Math.pow(a, 3));
// cos i を計算
// dOmegadt_required = - (3/2) * J2 * (RE/a)^2 * n * cos i
// → cos i = - (dOmegadt_required) / [ (3/2) * J2 * (RE/a)^2 * n ]
const cos_i = -dOmegadt_required / ((3 / 2) * J2 * Math.pow(R_EARTH / a, 2) * n);
// 防衛的に cos_i を [-1,1] にクランプ
const clampedCosI = Math.max(-1, Math.min(1, cos_i));
// i (rad) を計算
const i_rad = Math.acos(clampedCosI);
// 太陽同期軌道は後退軌道 (i > 90°) となるため、
// 必要な傾斜角は 180° - i (deg)
const i_deg = toDegrees(i_rad);
return 180 - i_deg;
};
ユーザーの入力からDummyのTLEを生成
TLE(Two-Line Element Set、二行要素セット)という、人工衛星の軌道情報を表すフォーマットがあります。 NASAやNORAD(北米航空宇宙防衛司令部)によって管理・公開されています。
先程の自分で決めた衛星のオレオレ情報を、このフォーマットに変換しておくと 他の人工衛星ライブラリを利用できるようになります。ここでも厳密性は問わないので衛星のスピードの減衰は0にしていたりかなり簡易化しています。
/**
* ユーザー入力からダミーTLEを生成する関数
* @param sat ユーザーが入力した衛星パラメータ
* @returns { line1: string, line2: string } ダミーTLEの2行
*/
const generateDummyTLE = (sat: SatelliteInput): { line1: string; line2: string } => {
// 'sun-synchronous' の場合は打ち上げ傾斜角を 97.8 固定
const inclination = sat.orbitType === ORBIT_TYPES.SUN_SYNCHRONOUS ? calculateSunSyncInclination(sat.altitude) : sat.launchAngle;
if (sat.orbitType === ORBIT_TYPES.SUN_SYNCHRONOUS) sat.launchAngle = inclination;
// RAAN を打ち上げ経度として簡易設定
const raan = sat.launchLon;
//const eccentricity = 0; // 円軌道と仮定
const argPerigee = 0; // 近地点引数:0
const meanAnomaly = 0; // 平均近点角:0
// 平均運動 (revs per day) の計算
const semiMajorAxis = R_EARTH + sat.altitude; // km
const n = Math.sqrt(MU / Math.pow(semiMajorAxis, 3)); // rad/s
const meanMotion = (n * 86400) / (2 * Math.PI); // revs per day
sat.meanMotion = meanMotion;
console.log(`alt:${sat.altitude},maj:${semiMajorAxis},n:${n},mot:${meanMotion}`);
// Epoch の生成(TLE epoch は YYDDD.DDDDDDDD 形式)
const now = new Date();
const year = now.getUTCFullYear() % 100; // 下2桁
const startOfYear = new Date(Date.UTC(now.getUTCFullYear(), 0, 1));
const dayOfYear = Math.floor((now.getTime() - startOfYear.getTime()) / (1000 * 60 * 60 * 24)) + 1;
const secondsOfDay = now.getUTCHours() * 3600 + now.getUTCMinutes() * 60 + now.getUTCSeconds() + now.getUTCMilliseconds() / 1000;
const fraction = secondsOfDay / 86400;
// Epoch を "YYDDD.DDDDDDDD" 形式に整形(ここでは小数部は 8 桁固定)
const epoch = `${year.toString().padStart(2, "0")}${dayOfYear.toString().padStart(3, "0")}.${fraction.toFixed(8).slice(2)}`;
// ダミーの衛星番号("00001" で固定)
const satNum = "00001";
// TLE Line 1(フォーマットの厳密なチェックディジット計算などは省略)
const line1 = `1 ${satNum}U 00000A ${epoch} .00000000 00000-0 00000-0 0 9991`;
// TLE Line 2 の各項目は所定の桁数で埋める必要があります。
// 以下は簡易フォーマット例です。
// - Inclination: 8桁(例:" 97.8000")
// - RAAN: 8桁
// - Eccentricity: 7桁(小数点なし、0の場合は"0000000")
// - Argument of Perigee: 8桁
// - Mean Anomaly: 8桁
// - Mean Motion: 11桁(小数点含む)
const inclStr = inclination.toFixed(4).padStart(8, " ");
const raanStr = raan.toFixed(4).padStart(8, " ");
const eccStr = "0000000"; // ecc = 0
const argPerigeeStr = argPerigee.toFixed(4).padStart(8, " ");
const meanAnomalyStr = meanAnomaly.toFixed(4).padStart(8, " ");
const meanMotionStr = meanMotion.toFixed(8).padStart(11, " ");
const line2 = `2 ${satNum} ${inclStr} ${raanStr} ${eccStr} ${argPerigeeStr} ${meanAnomalyStr} ${meanMotionStr}`;
return { line1, line2 };
};
DummyTLEから軌道を生成
TLEの情報があると、簡易的にSGP (Simplified General Perturbation) 計算で衛星の軌道を出すことができるようになります。この計算をJavaScriptで実行してくれるありがたいライブラリが下記です。
Readmeに紹介されいた下記などを読み進めると理解が深まりそうです。
Satellite Times
Satellite.jsを利用すると、ユーザーの入力から、DummyのTLEを生成し、軌道を生成する処理は下記のようにシンプルに実装できます。
ssimulationComponent
import * as satellite from "satellite.js";
/**
* computedSatellites: ユーザー入力(SatelliteInput)からダミーTLEを生成し、satellite.js を利用して
* シミュレーション時刻における衛星の地上トラック(緯度・経度の配列)を算出する computed プロパティの例
*/
const computedSatellites = computed<SatelliteOrbit[]>(() => {
// ここでは、satellites.value は SatelliteInput[] 型の配列とする(ユーザー入力済み)
// ※以下は例として、入力データの配列を想定
// 例:
// const satellites = ref<SatelliteInput[]>([
// { orbitType: 'inclined', launchLat: 30, launchLon: 140, altitude: 500, launchAngle: 0 },
// { orbitType: 'sun-synchronous', launchLat: 0, launchLon: 0, altitude: 600, launchAngle: 5 },
// ]);
return satellitesRef.value.map((satInput) => {
// ダミーTLEを生成
const { line1, line2 } = generateDummyTLE(satInput);
// TLE から satrec を作成(SGP4 propagator を内部的に使用)
const satrec = satellite.twoline2satrec(line1, line2);
const orbitData: Array<{ lat: number; lng: number }> = [];
// シミュレーション開始時刻(現在時刻)
const startTime = new Date();
// SIM_DURATION ステップ分ループ
for (let t_sim = 0; t_sim <= SIM_DURATION; t_sim++) {
// 各ステップの実時間(秒)に換算
const t_offset_sec = t_sim * TIME_SCALE;
const currentTime = new Date(startTime.getTime() + t_offset_sec * 1000);
// propagate() を用いて ECI 座標(位置、速度)を計算
const posVel = satellite.propagate(satrec, currentTime);
if (posVel.position && typeof posVel.position !== "boolean") {
// ECI 座標から GMST (Greenwich Mean Sidereal Time) を計算
const gmst = satellite.gstime(currentTime);
// ECI 座標を地球固定座標(ジオデティック:緯度、経度、高度)に変換
const geodetic = satellite.eciToGeodetic(posVel.position, gmst);
// 緯度・経度を度単位に変換
const lat = satellite.degreesLat(geodetic.latitude);
const lon = satellite.degreesLong(geodetic.longitude);
orbitData.push({ lat, lng: lon });
}
}
return { orbitData };
});
});
2D/3D 地図上での表示
さあ、早速計算した軌道をMapBoxの地図で表示してみましょう。
-
2D map mode
-
3D map mode

mapBox でAPITokenを取得して2D/3D表示切り替えのVue MapComponent基本部分
<div v-if="map">
<SatelliteComponent v-for="(sat, index) in satellites" :key="index" :map="map as any" :orbit-data="sat.orbitData" />
</div>
<div class="controls">
<button @click="toggle3D">
{{ is3D ? "Switch to 2D" : "Switch to 3D" }}
</button>
</div>
...
setup(props) {
const map = ref<mapboxgl.Map | null>(null);
const is3D = ref(true);
onMounted(() => {
mapboxgl.accessToken = props.accessToken;
const m = new mapboxgl.Map({
container: "map",
style: "mapbox://styles/mapbox/satellite-v9",
center: [0, 0],
zoom: 1.5,
projection: "globe",
pitch: 0,
bearing: 0,
});
if (m) {
m.on("style.load", () => {
map.value?.setFog({
color: "rgba(0,0,0,0)",
"high-color": "#f8f0e3",
"space-color": "#d8e2dc",
range: [1, 12],
"horizon-blend": 0.5,
});
});
}
map.value = m;
});
onBeforeUnmount(() => {
if (map.value) map.value.remove();
});
const toggle3D = () => {
is3D.value = !is3D.value;
map.value?.setProjection(is3D.value ? "globe" : "mercator");
};
return { map, is3D, toggle3D };
},
軌道を描画するSatelliteComponentは下記のコードでアニメーション表示できます
setup(props) {
let satelliteMarker: mapboxgl.Marker | null = null;
let animationFrame = 0;
let animationIndex = 0;
// 複数インスタンス同士が衝突しないようにランダムなソース/レイヤー ID を生成
const orbitSourceId = `satOrbitSource-${Math.random().toString(36).substring(2, 7)}`;
const orbitLayerId = `satOrbitLayer-${Math.random().toString(36).substring(2, 7)}`;
const createOrbitLine = () => {
// GeoJSON Feature として properties を必ず設定
const geojson: Feature<LineString, Record<string, unknown>> = {
type: "Feature", // リテラル "Feature" を指定
geometry: {
type: "LineString", // リテラル "LineString" を指定
coordinates: props.orbitData.map(point => [point.lng, point.lat]),
},
properties: {},
};
if (props.map.getSource(orbitSourceId)) {
(props.map.getSource(orbitSourceId) as mapboxgl.GeoJSONSource).setData(geojson);
} else {
props.map.addSource(orbitSourceId, {
type: 'geojson',
data: geojson,
});
}
};
const startAnimation = () => {
animationIndex = 0;
let lastUpdateTime = performance.now();
const animate = (currentTime: number) => {
// 現在の時刻と前回更新時刻の差が300ミリ秒以上なら更新
if (currentTime - lastUpdateTime >= 300) {
lastUpdateTime = currentTime; // 更新時刻を記録
if (animationIndex < props.orbitData.length) {
const { lng, lat } = props.orbitData[animationIndex];
satelliteMarker?.setLngLat([lng, lat]);
animationIndex++;
} else {
animationIndex = 0;
}
}
animationFrame = requestAnimationFrame(animate);
};
animationFrame = requestAnimationFrame(animate);
};
...
さあ、これで任意の衛星情報で軌道を表示できるようになりました。
とくに3Dで地球儀をグリグリ回して軌道を確認できるのは楽しいですね。
任意の地上の地点AOIへの到達タイミングを計算してみよう
AOI(Area Of Interest) の描画
さて、次はAOIの描画です。
こちらは任意の緯度、経度を表示するのみなのでシンプルですね。
以下のようなAOIComponentを追加して 青い点として描画しています。
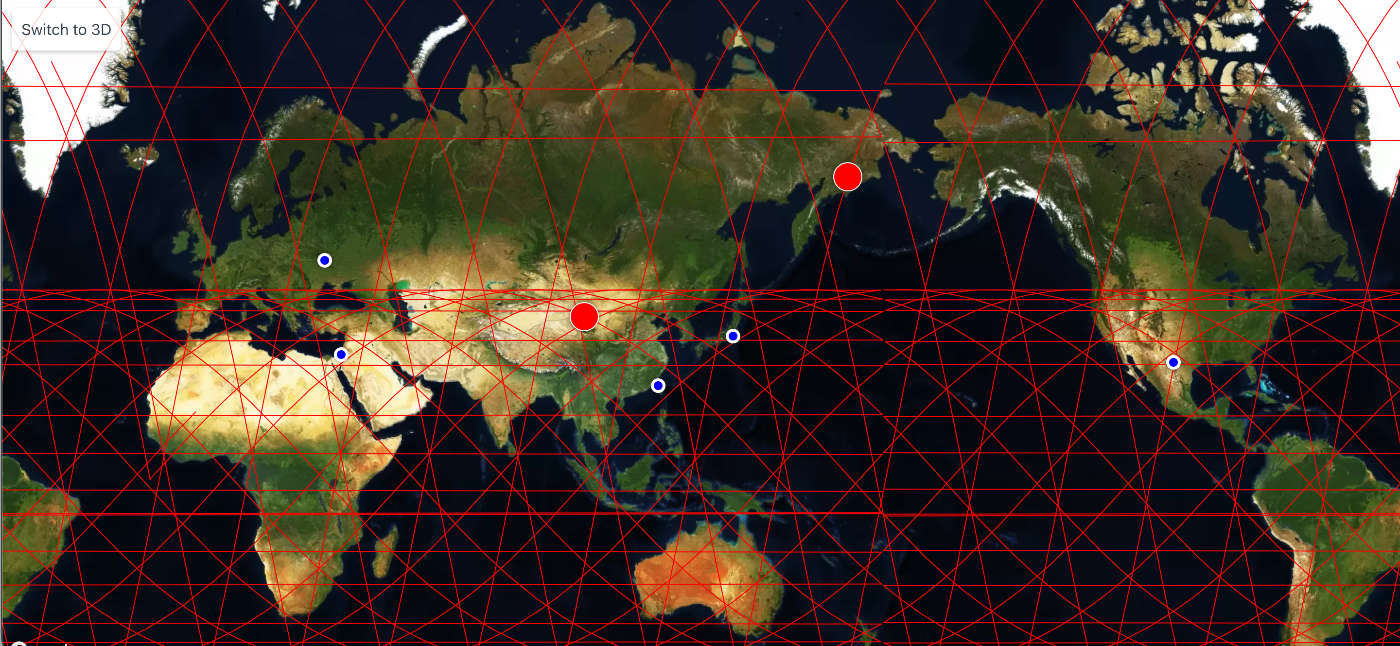
任意のAOIを追加して、衛星の撮像タイミングをSimulationできるようにします。
また、初期値として下記の現代の地政学上のホットスポットと東京を追加しておきます。
const aois = ref<AOI[]>([
{ lat: 35.77, lon: 139.82 }, //Tokyo
{ lat: 24.33, lon: 119.78 }, //Taiwan
{ lat: 50.45, lon: 30.52 }, //Ukraine
{ lat: 31.58, lon: 34.98 }, //Israel
{ lat: 29.77, lon: -102.45 }, //USA-Mexico
]);
SAR衛星が撮像できるタイミングは意外と少ない
SAR衛星の原理上OffNadirが15-50度で対象のほぼ真横を飛んでいるときだけ撮像できます。
上から見下ろした時の撮像可能エリア概念図

真横から衛星と、撮像対象エリアを見た時の概念図
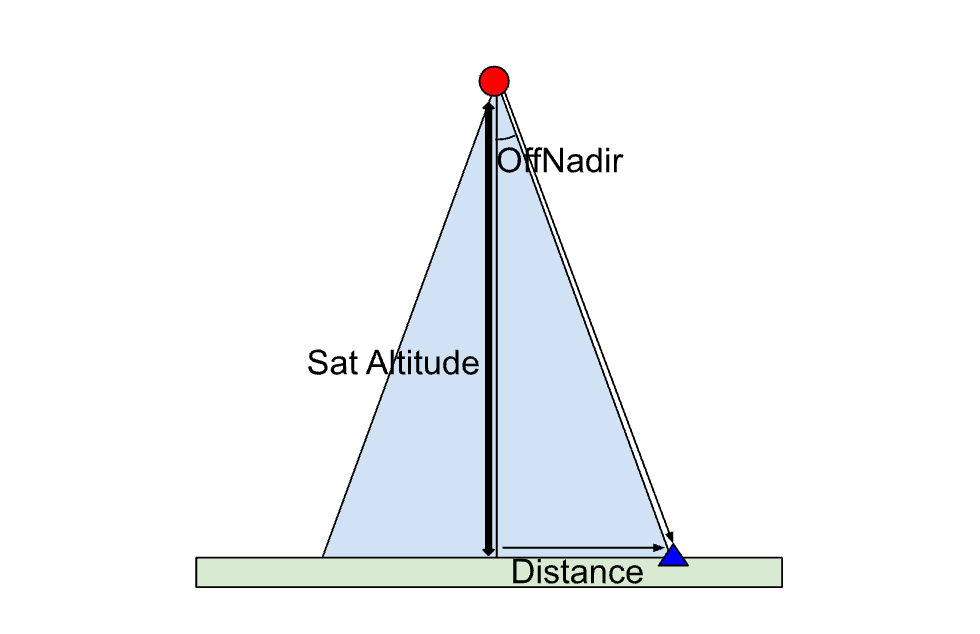
OffNadirを大きくすればするほど撮像できる範囲は広くなりますが、
電波強度的にも意味のあるデータとしては上限45-50度になります。
この関係を軌道情報と、AOI情報から計算して、真横になり、かつOffNadirが15-50 に収まっているタイミングを総計算させます。
まず、衛星の現在の位置と次の位置から向きを計算します。
/**
* 2点 (lat1, lon1) から (lat2, lon2) までの方位角(真北から時計回り、度)を計算
*/
const computeBearing = (lat1: number, lon1: number, lat2: number, lon2: number): number => {
const φ1 = toRadians(lat1);
const φ2 = toRadians(lat2);
const Δλ = toRadians(lon2 - lon1);
const y = Math.sin(Δλ) * Math.cos(φ2);
const x = Math.cos(φ1) * Math.sin(φ2) - Math.sin(φ1) * Math.cos(φ2) * Math.cos(Δλ);
let θ = Math.atan2(y, x);
// 角度に変換し、0~360度の範囲に正規化
θ = (toDegrees(θ) + 360) % 360;
return θ;
};
その向かっている向きの右側、左側それぞれの角度と、
衛星と、AoIの角度の差が設定値以内におさまっているかを判定します。
const lateralTolerance = 9; // 真横条件の許容誤差(度)
const heading = computeBearing(currentPos.lat, currentPos.lng, nextPos.lat, nextPos.lng);
const lateral1 = (heading + 90) % 360;
const lateral2 = (heading + 270) % 360;
const bearingToAOI = computeBearing(currentPos.lat, currentPos.lng, aoi.lat, aoi.lon);
const diff1 = angleDifference(bearingToAOI, lateral1);
const diff2 = angleDifference(bearingToAOI, lateral2);
if (diff1 <= lateralTolerance || diff2 <= lateralTolerance) {
おさまっていれば、地球の球面上での距離(haversineDistance)をもとめて、
それと、衛星の高度から、、arcTangentでoffNadirを求め、角度が範囲内であればその時刻を記録します。
const haversineDistance = (lat1: number, lon1: number, lat2: number, lon2: number): number => {
const dLat = toRadians(lat2 - lat1);
const dLon = toRadians(lon2 - lon1);
const a = Math.sin(dLat / 2) ** 2 + Math.cos(toRadians(lat1)) * Math.cos(toRadians(lat2)) * Math.sin(dLon / 2) ** 2;
const c = 2 * Math.atan2(Math.sqrt(a), Math.sqrt(1 - a));
return R_EARTH * c;
};
// Off-Nadir 角の計算
const distance = haversineDistance(currentPos.lat, currentPos.lng, aoi.lat, aoi.lon);
// offNadir = arctan(distance / altitude) (sat.altitude in km)
const offNadirDeg = toDegrees(Math.atan(distance / satellitesRef.value?.[satIndex].altitude));
if (offNadirDeg >= offNadirMin && offNadirDeg <= offNadirMax && (last ? i * TIME_SCALE_LOCAL - last > 600 : true)) {
imagingTimes.push(i * TIME_SCALE_LOCAL);
}
}
実際に計算させてみると、真横と判定するタイミングはたくさんあっても、対象との距離が長すぎてOffNadirが上限に収まるタイミングはとてもすくないということがよくわかります。
S1A4[2060] lat-23.17lon86.82 Distance: 18858.12 km, offNadirDeg: 88.33
S1A4[2357] lat27.15lon-100.29 Distance: 359.76 km, offNadirDeg: 33.19
S1A4[2358] lat27.54lon-99.77 Distance: 360.96 km, offNadirDeg: 33.28
S1A4[2657] lat-32.12lon74.95 Distance: 19677.10 km, offNadirDeg: 88.40
S1A4[2658] lat-32.46lon75.52 Distance: 19681.08 km, offNadirDeg: 88.40
S1A4[2958] lat36.71lon-108.57 Distance: 959.61 km, offNadirDeg: 60.18
S1A4[2959] lat37.01lon-107.92 Distance: 952.37 km, offNadirDeg: 59.99
S1A4[3262] lat-41.25lon71.38 Distance: 18643.82 km, offNadirDeg: 88.31
プログラムにすると複数地点、衛星を一気に計算してくれて便利です
プログラムにする一番の利点は、複数衛星X複数AOIという面倒な計算を 総当たりで高速に計算してくれるところです。
太陽同期軌道に1機、 傾斜軌道 45, 60 度に1機づつ投入したときに 平均、最遅の撮像感覚はかきのように計算してくれます。 これをみると、太陽同期(SatIndex0)よりも傾斜軌道(Index1,2)のほうが現在の地政学ホットスポットに対して 平均待ち時間、撮像回数ともに多くなるということが計算できていることが確認できました。
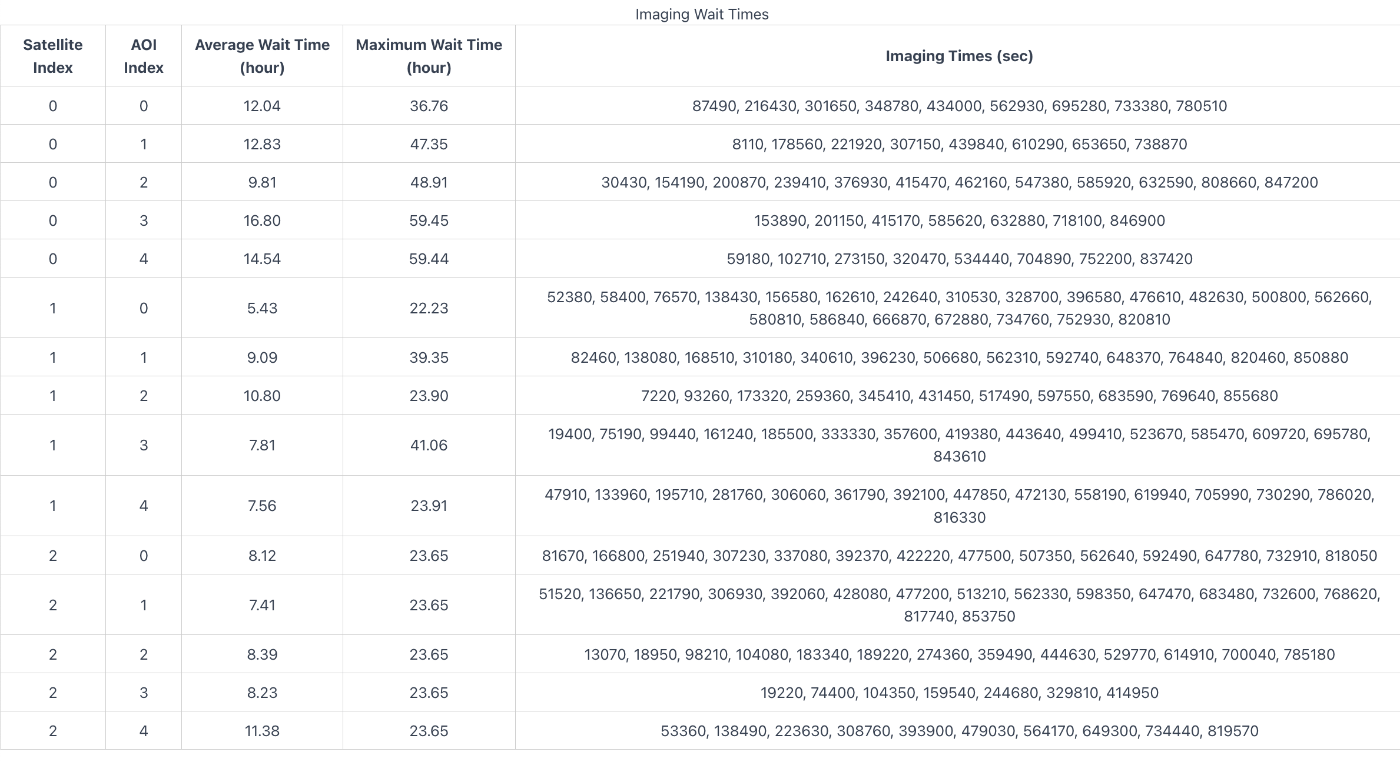
ちなみにある程度候補を出すには10日程度の軌道を計算させる必要がありますが、
それを描画すると地球は毛糸玉のような状態になってしまいます。。

今回のまとめ
地球観測衛星のビジネスゲームにおいて、どの地域をどの程度の待ち時間で何回撮像チャンスがあるかということは 重要な資源になります。 そして衛星事業者はどういう軌道に衛星を投入するかという選択肢があります。 入力と結果が、計算ができるようになったことでゲームのリアリティをぐっと引き上げることができる目処ができました。
次の展開として下記をつくっていこうとおもいます。
- 上記の計算結果によってビジネスの成果がどのようにかわるのか金額換算のモデル作成
- 撮像機会が計算できるようになったので10機をどのように打ち上げるとどの平均撮像待ち時間を短縮できるか最適化問題として解かせてみる
単純にここまでの機能でも人工衛星の基本事項理解に役立つ気がするので一旦公開してみようとおもいます。
人工知能を活用したアプリケーションやサービスを活用し、内発的動機付けで行動するエンジニア、起業家、社会起業家をサポートするコミュニティーです。 singularitysociety.org Supported by 週刊 Life is beautiful
Discussion