確率質量分布
ベルヌーイ試行をn 回行って成功する回数 X が従う確率分布として二項分布が知られている. 確率質量分布は以下である.
\begin{align*}
Bin(x | n, \mu) &= \binom{n}{x} \mu^x (1-\mu)^{1-x}
\\
\text{where} \; \binom{n}{x} &\equiv \frac{n!}{x!(n-x)!}\\
\end{align*}
ただし, 試行回数, 成功回数, 成功率は以下を満たす.
\begin{align*}
n &\in \R^+\\
x &\in \{0,1,\cdots,n\}\\
0 &\leq \mu \leq 1\\
\end{align*}
期待値・分散
期待値・分散は定義から示すこともできるが, ベルヌーイ分布に独立同一に従う確率変数 X' の期待値, 分散の和と見ることで容易に示すことが出来る.
\begin{align*}
\mathbb{E}(X)
&=
\sum_{i=1}^N\mathbb{E}(X')\\
&=
\sum_{i=1}^N \mu
\\
&= n \mu
\\
\mathbb{V}(X)
&=
\sum_{i=1}^N\mathbb{V}(X')\\
&=
\sum_{i=1}^N \mu(1-\mu)
\\
&= n \mu(1-\mu)
\end{align*}
期待値
定義から導出した場合は以下のようになる.
\begin{align*}
\mathbb{E}(X)
&=
\sum_{i=0}^n xP(X=x)\\
&=
0\cdot P(X=0)+\sum_{x=1}^nxP(X=x)\\
&=
\sum_{x=1}^n
x\frac{n!}{x!(n-x)!} \mu^x (1-\mu)^{n-x}
\\
&=
\sum_{x=1}^n
x\frac{n(n-1)!}{x(x-1)!(n-x)!} \mu\mu^{x-1} (1-\mu)^{n-x}
\\
&=
n\mu
\sum_{x'=0}^{n-1}
\frac{(n-1)!}{(x-1)!(n-x'-1)!} \mu^{x'} (1-\mu)^{n-x'-1}
\\
&=
n\mu
\sum_{x'=0}^{n'}
\frac{n'!}{(x-1)!(n'-x')!} \mu^{x'} (1-\mu)^{n'-x'}
\\
&=
n\mu
\sum_{x'=0}^{n'}
P(x')
\\
&=
n\mu
\end{align*}
5行目では x' = x-1 とおいている. ここで和の区間が 0 から n-1 になることに注意する.
6行目では n' = n-1 とおいている. そうすることで確率質量の総和となり除去できる.
分散
二次のモーメントを以下のように分解する.
\begin{align*}
\mathbb{E}(X^2)
&=
\sum_{x=0}^n x^2P(X=x)\\
&=
0 \cdot P(X=0) + \sum_{x=1}^n x^2P(X=x)\\
&=
\sum_{x=1}^n
x^2
\frac{n!}{x!(n-x)!}
\mu^x(1-\mu)^{n-x}
\\
&=
\sum_{x=1}^n
x^2
\frac{n!}{x(x-1)!(n-x)!}
\mu^x(1-\mu)^{n-x}
\\
&=
\sum_{x=1}^n
x
\frac{n!}{(x-1)!(n-x)!}
\mu^x(1-\mu)^{n-x}
\\
&=
\sum_{x=1}^n
\{(x-1)+1\}
\frac{n!}{(x-1)!(n-x)!}
\mu^x(1-\mu)^{n-x}
\\
&=
\sum_{x=1}^n
(x-1)
\frac{n!}{(x-1)!(n-x)!}
\mu^x(1-\mu)^{n-x}
+
\sum_{x=1}^n
\frac{n!}{(x-1)!(n-x)!}
\mu^x(1-\mu)^{n-x}
\\
\end{align*}
最終行右辺第二項(以下右辺第二項)は先ほどの期待値の式の途中式と同じである為同様に変形できる. (プライム記号の意味は前述のものと同じである.)
\begin{align*}
\text{(右辺第二項)}
&=
\sum_{x=1}^n
\frac{n!}{(x-1)!(n-x)!}
\mu^x (1-\mu)^{n-x}
\\
&=
\sum_{x'=0}^{n-1}
\frac{n(n-1)!}{x'!(n-x'-1)!}
\mu\mu^{x-1} (1-\mu)^{n-x'-1}
\\
&=
n\mu
\sum_{x'=0}^{n-1}
\frac{(n-1)!}{x'!(n-x'-1)!}
\mu^{x-1} (1-\mu)^{n-x'-1}
\\
&=
n\mu
\sum_{x'=0}^{n'}
\frac{n'!}{x'!(n'-x')!}
\mu^{x-1} (1-\mu)^{n'-x'}
\\
&=
n\mu
\end{align*}
よって最終行右辺第一項(以下右辺第一項)を求めればよいことが分かる
\begin{align*}
\text{(右辺第一項)}
&=
0\cdot
\frac{n!}{0!n!}
\mu^0 (1-\mu)^{n}
+
\sum_{x=2}^n
(x-1)
\frac{n!}{(x-1)!(n-x)!}
\mu^x (1-\mu)^{n-x}
\\
&=
\sum_{x=2}^n
(x-1)
\frac{n(n-1)(n-2)!}{(x-1)(x-2)!(n-x)!}
\mu^2\mu^{x-2} (1-\mu)^{n-x}
\\
&=
n(n-1)\mu^2
\sum_{x=2}^n
\frac{(n-2)!}{(x-2)!(n-x)!}
\mu^{x-2} (1-\mu)^{n-x}
\\
&=
n(n-1)\mu^2
\sum_{x'=0}^{n-2}
\frac{(n-2)!}{(x''-2)!(n-x''-2)!}
\mu^{x''-2} (1-\mu)^{n-x''-2}
\\
&=
n(n-1)\mu^2
\sum_{x''=0}^{n''}
\frac{n''!}{(x''-2)!(n''-x'')!}
\mu^{x''-2} (1-\mu)^{n''-x''}
\\
&=
n(n-1)\mu^2
\end{align*}
1行目では総和を x=1 のときとその他で分けると x=1 の項が 0 になることを用いている
3行目では x'' = x-2 とおいている. ここで和の区間が 0 \leq x'' \leq n-2 になることに注意する.
4行目では n'' = n-2 とおいている.
以上より, 二次のモーメントは以下の式で表すことが出来る.
\mathbb{E}(X^2) =n(n-1)\mu^2 - n\mu
よって分散は,
\begin{align*}
\mathbb{V}(X)
&=
\mathbb{E}(X^2) -\mathbb{E}(X)^2\\
&=
n(n-1)\mu^2+ n\mu - (n\mu)^2\\
&=
n\mu\{(n-1)\mu + 1 - n\mu\}\\
&=
n\mu(1-\mu)
\end{align*}
積率母関数
積率母関数(モーメント母関数)を用いると期待値・分散の導出が完結にできることがある. 二項分布の場合, 置換をする必要がなくなるが, 二項分布の場合, ベルヌーイ分布の多試行と見た方が期待値・分散の導出が楽である. 正規分布などでは置換積分や部分積分などといった複雑な計算を避けることが出来る.
積率母関数の定義に基づいて二項分布の積率母関数を導出する.
\begin{align*}
M_X(t)
&=
\mathbb{E}(e^{tX})\\
&=
\sum_{x=0}^n
e^{tx}
\frac{n!}{x!(n-x)!}
\mu^x (1-\mu)^{n-x}
\\
&=
\sum_{x=0}^n
\frac{n!}{x!(n-x)!}
(e^t\mu)^x (1-\mu)^{n-x}
\\
&=
\{(e^t\mu)+(1-\mu)\}^n
\end{align*}
最終行は二項定理を用いている. 二項定理は以下に示す通りである.
(a+b)^n = \sum_{k=0}^n \frac{n!}{k!(n-k)!} a^k b^{1-k}
試しに n =2 で計算をしてみると,
\begin{align*}
(a+b)^2
&=
(a+b)(a+b)
\\
&=
a^2+2ab+b^2
\\
(a+b)^2
&=
\sum_{k=0}^2
\frac{2!}{k!k-2!} a^k b^{2-k}
\\
&=
\frac{2!}{0!(0-2)!} a^0 b^{2-0}
+
\frac{2!}{1!(1-2)!} a^k b^{2-1}
+
\frac{2!}{2!(2-2)!} a^2 b^{2-2}
\\
&=
a^2+2ab+b^2
\end{align*}
期待通りの数値になっていることが分かる. 導出した積率母関数を用いて期待値と分散を導出する.
積率母関数を用いて期待値・分散を求める. モーメント母関数にはk回tで微分した式が t=0 の近傍でk次のモーメントになるという性質があるので以下のように導出できる.
\begin{align*}
\mathbb{E}(X)
&=
M_X(t)'|_{t=0}
\\
&=
(\{
(e^t\mu+(1-\mu)
\}^n)'|_{t=0}
\\
&=
n
\{
e^t\mu+(1-\mu)
\}^{n-1}
(e^t\mu)'
|_{t=0}
\\
&=
n
\{
e^t\mu+(1-\mu)
\}^{n-1}
\mu
|_{t=0}
\\
&=
n\mu
\\
\end{align*}
\begin{align*}
\mathbb{E}(X^2)
&=
M_X(t)''|_{t=0}
\\
&=
(
n
\{
e^t\mu+(1-\mu)
\}^{n-1}
(e^t\mu)
)'
|_{t=0}
\\
&=
n(n-1)
\{
e^t\mu+(1-\mu)
\}^{n-2}
(e^t\mu)
(e^t\mu)
+
n\{
e^t\mu+(1-\mu)
\}^{n-1}
(e^t\mu)
|_{t=0}
\\
&=
n(n-1)
\{
e^0\mu+(1-\mu)
\}^{n-2}
(e^0\mu)
(e^0\mu)
+
n\{
e^0\mu+(1-\mu)
\}^{n-1}
(e^0\mu)
\\
&=
n(n-1)\mu^2
+
n\mu
\end{align*}
二回微分では積の微分が出てくるため, 計算が煩雑になる為注意する必要がある.
以上より,
\begin{align*}
\mathbb{V}(X)
&=
\mathbb{E}(X^2) -\mathbb{E}(X)^2\\
&=
n(n-1)\mu^2+ n\mu - (n\mu)^2\\
&=
n\mu\{(n-1)\mu + 1 - n\mu\}\\
&=
n\mu(1-\mu)
\end{align*}
最尤推定
対数尤度関数の導出
二項分布に独立同一に従う確率変数の観測値 x_i を要素に持つデータを以下のように定義する. n が試行回数である為, 以降, N がデータの要素数であることに注意すると良い.
\mathbb{x} = \{ x_1 x_2 \cdots x_N\}
このとき対数尤度関数は,
\begin{align*}
\ln L(\mu)
&=
\ln p(\mathbf{x}|\mu)
\\
&=
\ln \prod_{i=1}^N
p(x_i)
\\
&=
\ln \prod_{i=1}^N
\{
\binom{n}{x_i}\;\mu^x_i \;(1-\mu)^{n-x_i}
\}
\\
&=
\sum_{i=1}^N
\{
\ln\mu^x_i+\ln(1-\mu)^{n-x_i}
\}+\text{const.}
\\
&=
\sum_{i=1}^N
\{
x_i\ln\mu+(n-x_i)\ln(1-\mu)
\}+\text{const.}
\\
&=
\sum_{i=1}^N
x_i\ln\mu
+
\sum_{i=1}^N
(n-x_i)\ln(1-\mu)
+
\text{const.}
\\
&=
\sum_{i=1}^N
x_i\ln\mu
+
(nN-
\sum_{i=1}^N
x_i)
\ln(1-\mu)
+
\text{const.}
\end{align*}
最尤推定量の導出
導出した対数尤度関数をパラメータで微分すると尤度方程式が得られる. 尚, 尤度方程式とは対数尤度関数の極値条件を与える方程式のことである. この尤度方程式の解が最尤推定量となる.
対数尤度関数を微分すると以下の式が得られる
\begin{align*}
\frac{\partial}{\partial \mu}\ln L(\mu)
&=
\frac{\partial}{\partial \mu}
\sum_{i=1}^N
x_i\ln\mu
+
\frac{\partial}{\partial \mu}
(nN-
\sum_{i=1}^N
x_i)
\ln(1-\mu)
+
\frac{\partial}{\partial \mu}
\text{const.}
\\
&=
\frac{1}{\mu}\sum_{i=1}^N
x_i
-
(nN-
\sum_{i=1}^N
x_i)
\frac{1}{(1-\mu)}
\end{align*}
対数尤度関数の極値はこの式が 0 の時であるから, 以下を満たす \mu_{ML} を導出する.
\frac{1}{\mu}\sum_{i=1}^N
x_i
-
(nN-
\sum_{i=1}^N
x_i)
\frac{1}{(1-\mu)}=0
これを満たす \mu = \mu_{ML} は,
\begin{align*}
\frac{1}{\mu_{ML}} \sum_{i=1}^N x_i
&=
(Nn-\sum_{i=1}^N x_i)
\frac{1}{1-\mu_{ML}}
\\
\frac{1-\mu_{ML}}{\mu_{ML}}
&=
\frac{(Nn-\sum_{i=1}^N x_i)}{\sum_{i=1}^N x_i}
\\
\frac{1}{\mu_{ML}}-1
&=
\frac{Nn}{\sum_{i=1}^N x_i}-1
\\
\mu_{ML}
&=
\frac{\sum_{i=1}^N x_i}{Nn}
\end{align*}
これはベルヌーイ試行の成功回数をベルヌーイ試行の試行回数で割っていることになるので成功回数の平均である.
可視化
nを変化させたときの分布
はじめに\mu を固定して, n を変化させて観察を行う. 下記は二項分布 Bin(x|n,0.5)からサンプリングしそれぞれの成功回数の確率を可視化したものである.
期待値も分散も n についてみれば一次関数なので n が増えれば期待値も分散も大きくなることが考えられる. 以上の予想を実際に観察し, 確認する.
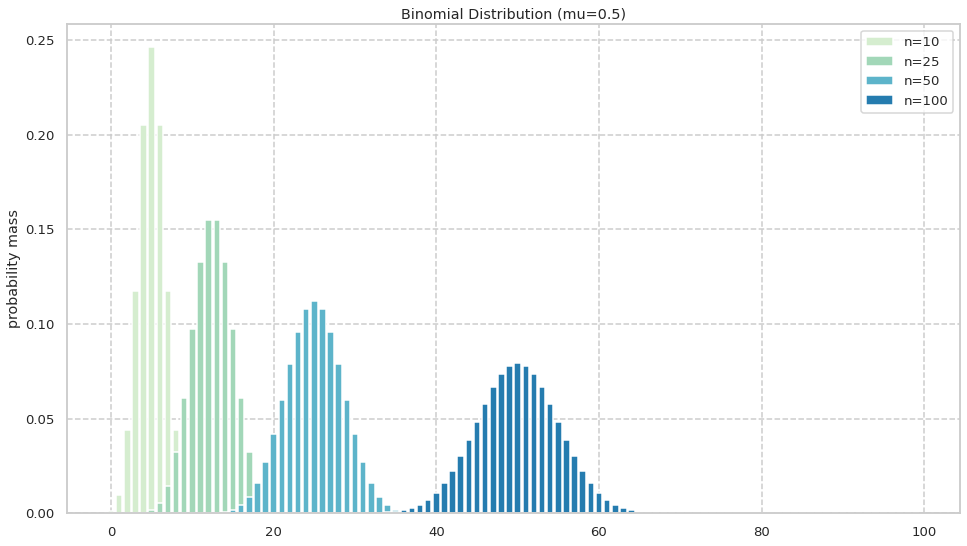
図からは概ね予想通りであることが読み取れる.
また, 二項分布にはn が十分大きいときに N(n\mu,n\mu(1-\mu)) で近似することができる性質が知られているが, これも確認することができる.
以下コード
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import binom
x = np.arange(0, 100, 1)
p = 0.5
k = 50
ys = []
for n in [10,25,50,100]:
y = [binom.pmf(k, n, p, loc=0) for k in x]
ys.append(y)
sns.set()
sns.set_style("whitegrid", {'grid.linestyle': '--'})
sns.set_context("talk", 0.8, {"lines.linewidth": 0})
sns.set_palette("GnBu", 4, 0.9)
fig=plt.figure(figsize=(16,9))
ax1 = fig.add_subplot(1, 1, 1)
ax1.set_title('Binomial Distribution (mu=0.5)')
ax1.set_ylabel('probability mass')
for y in ys:
ax1.bar(x, y)
ax1.legend(['n=10','n=25','n=50','n=100'])
plt.show()
\muを変化させたときの分布
同様にして\mu についても検証する. 二項分布 Bin(x|100,\mu)からサンプリングしそれぞれの成功回数の確率を可視化を行う.
期待値に関しては一次関数なので\mu が大きいほど大きくなることが予想される. また, 分散に関してはn を 1 に固定すれば\mu(1-\mu) という二次関数となる. この関数は以下のように \mu =0,1 で 0 を取り, \mu = 0.5 で最大を取る. よって分散も \mu =0,1 で 0 を取り, \mu = 0.5 で最大を取ることが予想される.
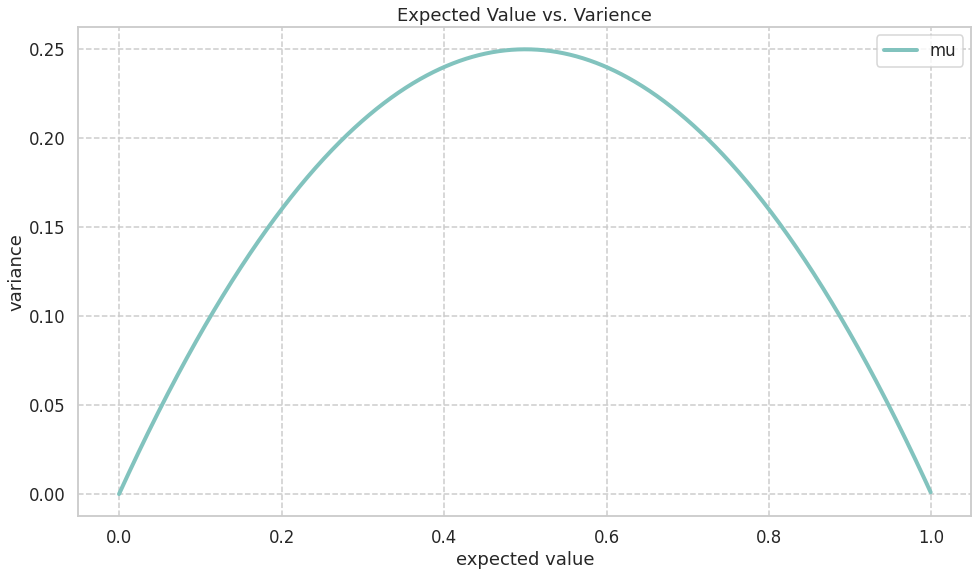
以上の予想を実際に観察し, 確認する.
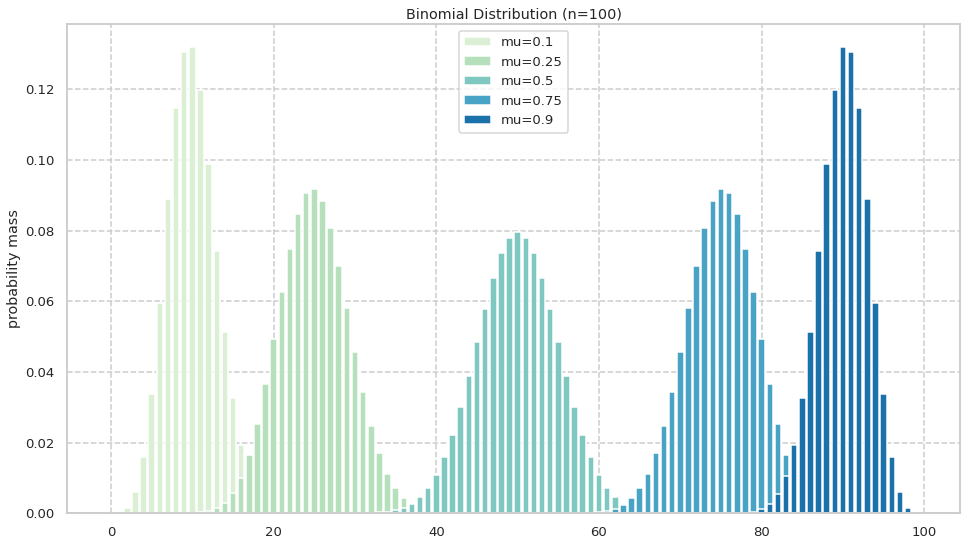
図からは概ね予想通りであることが読み取れる.
以下コードである. ただし, 使用したライブラリが同じなのでimport部分は省略している.
x = np.arange(0, 100, 1)
n = 100
k = 5
ys = []
for p in [0.1,0.25,0.50,0.75,0.9]:
y = [binom.pmf(k, n, p, loc=0) for k in x]
ys.append(y)
sns.set()
sns.set_style("whitegrid", {'grid.linestyle': '--'})
sns.set_context("talk", 0.8, {"lines.linewidth": 0})
sns.set_palette("GnBu", 5, 0.9)
fig=plt.figure(figsize=(16,9))
ax1 = fig.add_subplot(1, 1, 1)
ax1.set_title('Binomial Distribution (n=100)')
ax1.set_ylabel('probability mass')
for y in ys:
ax1.bar(x, y)
ax1.legend(['mu=0.1','mu=0.25','mu=0.5','mu=0.75','mu=0.9'])
plt.show()
参考文献
(1) 竹村彰通.”新装改訂版 現代数理統計学”.2020.学術図書出版社
(2) 一般社団法人 日本統計学会.”日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブック”.2020.学術図書出版社
(3) 一般社団法人 日本統計学会.”日本統計学会公式認定 統計検定1級対応 統計学”.2013.東京図書出版社
(4)C.M.ビショップ.”パターン認識と機械学習 上 ベイズ理論による統計的予測”.2019.丸善出版株式会社
(5)須山敦志.”機械学習スタートアップシリーズ ベイズ推論による機械学習入門”.2018.株式会社講談社サイエンティフィク
参考サイト
(1) matplotlib document
(2) scipy document: scipy.stats.binom



Discussion