[統計学] 正規分布の期待値と分散(1次元)

概要

はじめに

Shunです. 統計や機械学習を勉強しています. 正規分布を計算上使うことが多いのでよく使う式をまとめてみました.

機械学習・統計学における位置づけ

正規分布(normal distribution)※1は連続型確率変数の分布のモデルとして広く利用されている. 出典(1), (2)によれば統計学上きわめて重要な確率分布と位置付けられている.

確率密度関数

正規分布の確率密度関数は以下のように書ける.

$$\mathcal{N}(x| \mu, \sigma^2) = \frac{1}{\sqrt{2\pi \sigma^2}} \exp \biggl\{{- \frac{(x-\mu)^2}{2\sigma^2}}\biggr\}$$

ただし, $\mu, \sigma^2$ は平均, 分散である. 特に $\mathcal{N}(x|0, 1)$ を標準正規分布という.

期待値

$$\mathbb{E}(X) = \mu$$

導出

$$\begin{align*}\mathbb{E}(X)&=\frac{1}{\sqrt{2\pi \sigma^2}}\int_{-\infty}^{\infty}x\exp \biggl[-\frac{1}{2}(x-\mu)\sigma^{-2}(x-\mu)\biggr]dx\\&=\frac{1}{\sqrt{2\pi \sigma^2}}\int_{-\infty}^{\infty}(z+\mu)\exp \biggl[-\frac{1}{2}z\sigma^{-2}z\biggr]dz\\&=\frac{1}{\sqrt{2\pi \sigma^2}}\int_{-\infty}^{\infty}z\exp \biggl[-\frac{1}{2}z\sigma^{-2}z\biggr]+\mu\exp \biggl[-\frac{1}{2}z\sigma^{-2}z\biggr]dz\\&=\frac{1}{\sqrt{2\pi \sigma^2}}\int_{-\infty}^{\infty}\mu\exp \biggl[-\frac{1}{2}z\sigma^{-2}z\biggr]dz\\&=\mu\frac{1}{\sqrt{2\pi\sigma^2}}\int_{-\infty}^{\infty}\exp \biggl[-\frac{1}{2}(x-\mu)\sigma^{-2}(x-\mu)\biggr]dx \\&=\mu\end{align*}$$

2行目では, $x- \mu=z$ と置換している.
4行目では, 第1項が奇関数を負の無限大から正の無限大に積分していることから0としている. なお, $\int z\exp z^2$は以下のような関数形になっている.

分散

$$\mathbb{E}(X^2)=\sigma^2$$

導出

期待値の時と同じように変形を進める.

$$\begin{align*}\mathbb{E}(X^2)&=\frac{1}{\sqrt{2\pi \sigma^2}}\int_{-\infty}^{\infty}x^2\exp \biggl[-\frac{1}{2}(x-\mu)\sigma^{-2}(x-\mu)\biggr]dx\\&=\frac{1}{\sqrt{2\pi \sigma^2}}\int_{-\infty}^{\infty}(z+\mu)^2\exp\biggl[-\frac{1}{2}z\sigma^{-2}z\biggr]dz\\\end{align*}$$

期待値の導出と同じ議論により, $z\mu, \mu z$の項は消え, $\mu^2$の項は$\mu^2$となる. よって$z^2$の項を求めれば, 求める値が得られることに注意する.

$$\begin{align*}(第一項)&=\frac{1}{\sqrt{2\pi \sigma^2}}\int_{-\infty}^{\infty}z^2\exp \biggl[-\frac{1}{2}z\sigma^{-2}z\biggr]dz\\&=\int_{-\infty}^{\infty}(x-\mu)^2\frac{1}{\sqrt{2\pi \sigma^2}}\exp\biggl[-\frac{1}{2}(x-\mu)\sigma^{-2}(x-\mu)\biggr]dx\\&=\int_{-\infty}^{\infty}\sigma^2 y^2\frac{1}{\sqrt{2\pi \sigma^2}}\exp\biggl[-\frac{1}{2}y^2\biggr]\sigma dy\\&=\frac{\sigma^2}{\sqrt{2\pi}}\int_{-\infty}^{\infty}y^2\exp (-\frac{1}{2}y^2) dy\\&=\frac{\sigma^2}{\sqrt{2\pi}}\int_{-\infty}^{\infty}-y(\exp (-\frac{1}{2}y^2))'dy\\&=\frac{\sigma^2}{\sqrt{2\pi}}\biggl(\big[-y \exp (-\frac{y^2}{2})\big]_{-\infty}^{\infty}-\int_{-\infty}^{\infty}(-1)\exp (-\frac{y^2}{2})\biggr)dy\\&=\sigma^2\int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi}}\exp (-\frac{y^2}{2})dy\\&=\sigma^2\end{align*}$$

1行目から4行目では$z^2$の項を$x$に戻し, $y=(x-\mu)/\sigma$ と変換している
4行目から5行目は部分積分をする準備の変形を行っており, 7行目で部分積分を行っている.
7行目から8行目では右辺第一項の四角括弧の内部が奇関数であることから0としている.
8行目から9行目は$\sigma^2$にかかっている部分が$y$の標準正規分布になっていることから積分値が1となり, 消去している.

以上の議論から,

$$\begin{align*}\mathbb{V}(X)&=\mathbb{E}(X^2)-\mathbb{E}(X)^2\\&=\sigma^2 + \mu^2-\mu^2\end{align*}$$

積率母関数

積率母関数(モーメント母関数)を用いると期待値分散の導出が非常に簡潔に書けるため導出方法を覚えておくと便利である. 特に試験では計算ミス防止に繋がるため活用すると良いと思われる. なお, 積率母関数の定義や性質については適宜文献(1)を参照されたい.

導出

$$\begin{align*}M_X(t)&=\int_{-\infty}^{\infty}\exp [tx]\frac{1}{\sqrt{2\pi \sigma^2}}\exp \biggl[-\frac{(x-\mu)^2}{2\sigma^2}\biggr]dx\\&=\int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi \sigma^2}}\exp \biggl[-tx-\frac{(x-\mu)^2}{2\sigma^2}\biggr]dx\\&=\int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi \sigma^2}}\exp \biggl[-\frac{-2\sigma^2 tx+x^2-2\mu x +\mu^2}{2\sigma^2}\biggr]dx\\&=\int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi \sigma^2}}\exp \biggl[-\frac{(x^2-2x[\mu+\sigma^2 t])+\mu^2}{2\sigma^2}\biggr]dx\\&=\int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi \sigma^2}}\exp \biggl[-\frac{(x-[\mu+\sigma^2 t])^2-(\mu + \sigma t)^2+\mu^2}{2\sigma^2}\biggr]dx\\&=\exp \biggl[\frac{(\mu + \sigma t)^2-\mu^2}{2\sigma^2}\biggr]\int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi \sigma^2}}\exp \biggl[-\frac{(x-[\mu+\sigma^2 t])^2}{2\sigma^2}\biggr]dx\\&=\exp \biggl[\frac{2\mu \sigma^2 t + \sigma^4 t^2}{2\sigma^2} \biggl]\int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi \sigma^2}}\exp \biggl[-\frac{(x-[\mu+\sigma^2 t])^2}{2\sigma^2}\biggr]dx\\&=\exp \biggl[\mu t+\frac{\sigma^2 t^2}{2} \biggr]\end{align*}$$

3行目から5行目までは平方完成をしている.
7行目から8行目では積分部分が正規分布の負の無限大から正の無限大までの積分値となることから除去している.

積率母関数を用いて期待値分散を求める. モーメント母関数には$k$回$t$で微分した式が$t=0$の近傍で$k$次のモーメントになるという性質がある※(3)ので以下のように導出できる.

積率母関数を用いた一次のモーメント(期待値)の導出

$$\begin{align*}\mathbb{E}(X)&=\exp \biggl[\mu t + \frac{\sigma^2 t^2}{2}\biggr]'|_{t=0}\\&=(\mu t + \frac{\sigma^2 t^2}{2})'\exp \biggl[\mu t + \frac{\sigma^2 t^2}{2}\biggr]|_{t=0}\\&=(\mu+ \sigma^2 t)\exp \biggl[\mu t + \frac{\sigma^2 t^2}{2}\biggr]|_{t=0}\\&=\mu\end{align*}$$

積率母関数を用いた二次のモーメントの導出

$$\begin{align*}\mathbb{E}(X^2)&=\exp \biggl[\mu t + \frac{\sigma^2 t^2}{2}\biggr]''|_{t=0}\\&=(\mu +\sigma^2 t)'\exp \biggl[\mu t + \frac{\sigma^2 t^2}{2}\biggr]+(\mu +\sigma^2 t)\exp \biggl[\mu t + \frac{\sigma^2 t^2}{2}\biggr]'|_{t=0}\\&=\sigma^2\exp \biggl[\mu t + \frac{\sigma^2 t^2}{2}\biggr]+(\mu +\sigma^2 t)^2\exp \biggl[\mu t + \frac{\sigma^2 t^2}{2}\biggr]'|_{t=0}\\&=\sigma^2+\mu^2\end{align*}$$

積率母関数を用いた分散の導出

$$\begin{align*}\mathbb{V}(X)&=\mathbb{E}(X^2)-\mathbb{E}(X)^2\\&=\sigma^2+\mu^2-\mu^2\\&=\sigma^2\end{align*}$$

最尤推定

最尤推定は統計学において最も標準的な統計的推定法と言われることもある強力な手法である.※(2) 最尤推定によってもたらされる最尤推定量は必ずよい推定量であるという保証はないものの, 多くの場合に合理的な推定量となる. ここでは正規分布のパラメータについて最尤推定量を導出する.

対数尤度関数の導出

以下の 独立に得られた $x_i \sim \mathcal{N}(\mu, \sigma^2)$ を要素に持つ $\mathbf{x}$ を観測したと仮定する.

$$\mathbf{x} = \{x_1 \;x_2 \;\cdots x_N\}$$

このとき, 同時確率は以下のように書ける.

$$\begin{align*}P(\mathbf{x})&=\prod_{i=1}^{N} p(x_i)\\&=\prod_{i=1}^{N} \mathcal{N}(x_i| \mu, \sigma^2)\\&=\prod_{i=1}^{N}\frac{1}{\sqrt{2\pi \sigma^2}}\exp \biggl[-\frac{(x_i -\mu)^2}{2\sigma^2}\biggr]\\&=\prod_{i=1}^{N}\exp \biggl[-\frac{1}{2}\ln 2\pi \sigma^2 -\frac{1}{2}(x_i -\mu)^2(\sigma^2)^{-1}\biggr]\\&=\prod_{i=1}^{N}\exp \biggl[-\frac{1}{2}\biggl(\ln 2\pi+\ln \sigma^2+(x_i -\mu)^2(\sigma^2)^{-1}\biggr)\biggr]\end{align*}$$

3行目から5行目の処理はこの後に行う計算の為にしている処理である.

平均の最尤推定量の導出

以上より対数尤度関数は

$$\begin{align*}\ln L(\mu)&=\sum_{i=1}^{N}-\frac{1}{2}\biggl(\ln 2\pi+\ln \sigma^2+(x_i -\mu)^2(\sigma^2)^{-1}\biggr)\\&=-\frac{1}{2}\sum_{i=1}^{N}\biggl((x_i -\mu)^2(\sigma^2)^{-1}\biggr)+\text{const.}\end{align*}$$

ただし, $\mu$ 以外を定数としてみていることに注意.
対数尤度関数を微分すると,

$$\begin{align*}\frac{\partial}{\partial \mu}\ln L(\mu)&=\frac{\partial}{\partial \mu}-\frac{1}{2\sigma^2}\sum_{i=1}^{N}\biggl(x_i^2 -2\mu x_i + \mu^2\biggr)+\text{const.}\\&=-\frac{1}{2\sigma^2}\sum_{i=1}^{N}\frac{\partial}{\partial \mu}\biggl(-2\mu x_i + \mu^2\biggr)\\&=-\frac{1}{2\sigma^2}\sum_{i=1}^{N}\biggl(-2x_i + 2\mu\biggr)\\&=-\frac{1}{2\sigma^2}\biggl[\sum_{i=1}^{N}\biggl(-2x_i\biggr)+2N\mu\biggr]\cdots (1)\end{align*}$$

ただし, 二行目の定数項の除去は微分によるものである.
(1)式を$0$とおくと

$$\begin{align*}-\frac{1}{2\sigma^2}\biggl[\sum_{i=1}^{N}\biggl(-2x_i\biggr)+2N\mu\biggr]&=0\\\biggl[\sum_{i=1}^{N}\biggl(-2x_i\biggr)+2N\mu\biggr]&=0\\-2\sum_{i=1}^{N}(x_i)+2N\mu&=0\\2N\mu&=2\sum_{i=1}^{N}x_i\\\mu&=\frac{1}{N}\sum_{i=1}^{N}x_i\\\end{align*}$$

以上より

$$\mu_{ML} =\frac{1}{N} \sum_{i=1}^N x_i$$

分散の最尤推定量の導出

$\mu$ を$\mu_{ML}$ とする. このとき, 対数尤度関数は

$$\begin{align*}\ln L(\sigma^2)&=\sum_{i=1}^{N}-\frac{1}{2}\biggl(\ln 2\pi+\ln \sigma^2+(x_i -\mu_{ML})^2(\sigma^2)^{-1}\biggr)\\&=-\frac{1}{2}\sum_{i=1}^{N}\biggl(\ln \sigma^2+(x_i -\mu_{ML})^2(\sigma^2)^{-1}\biggr)+\text{const.}\end{align*}$$

ただし, $\sigma^2$ 以外を定数としてみていることに注意.
対数尤度関数を微分すると,

$$\begin{align*}\frac{\partial}{\partial \mu}\ln L(\mu)&=\frac{\partial}{\partial \sigma^2}-\frac{1}{2}\sum_{i=1}^{N}\biggl(\ln \sigma^2+(x_i -\mu_{ML})^2(\sigma^2)^{-1}\biggr)+\text{const.}\\&=-\frac{1}{2}\sum_{i=1}^{N}\frac{\partial}{\partial \sigma^2}\biggl(\ln \sigma^2+(x_i -\mu_{ML})^2(\sigma^2)^{-1}\biggr)\\&=-\frac{1}{2}\sum_{i=1}^{N}\biggl(\frac{1}{\sigma^2}-(x_i -\mu_{ML})^2(\sigma^2)^{-2}\biggr)\cdots(2)\end{align*}$$

ただし, 二行目の定数項の除去は微分によるものである.
(2)式を$0$とおくと,

$$\begin{align*}-\frac{1}{2}\sum_{i=1}^{N}\biggl(\frac{1}{\sigma^2}-(x_i -\mu)^2(\sigma^2)^{-2}\biggr)&=0\\\frac{N}{\sigma^2}-\sum_{i=1}^{N}(x_i -\mu)^2(\sigma^2)^{-2}&=0\\\frac{N}{\sigma^2}&=\sum_{i=1}^{N}(x_i -\mu)^2(\sigma^2)^{-2}\\\frac{1}{\sigma^2}&=\frac{1}{N}\sum_{i=1}^{N}(x_i -\mu)^2(\sigma^2)^{-2}\\\sigma^2&=\frac{1}{N}\sum_{i=1}^{N}(x_i -\mu)^2\end{align*}$$

以上より

$$\sigma_{ML}^2=\frac{1}{N}\sum_{i=1}^{N}(x_i -\mu)^2$$

最尤推定解の期待値と不偏分散

ここで, 最尤推定解の期待値を評価すると以下のような結果になる. 分散の最尤推定量の期待値が$\sigma^2$ と一致していないことに注意する.

$$\begin{align*} \mathbb{E}(\mu_{ML}) &= \mu \\ \mathbb{E}(\sigma_{ML}^2) &= \frac{N-1}{N}\sigma^2 \end{align*}$$

パラメータと分布の形状

期待値, 分散について確認したので実際に分布の形状との関係を観察する.

$\mu$ を変化させたときの分布の形状

$\mu$ を変化させると分布の軸が変化する.

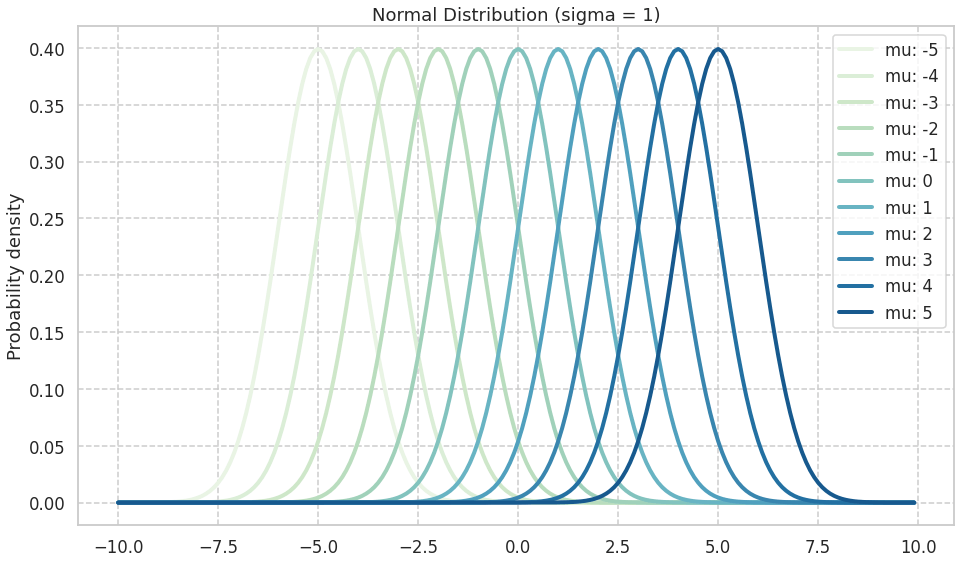
以下コード:

1. 初めに必要となるライブラリをimport.

import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
import seaborn as sns

2. グラフを描画.

sns.set()
sns.set_style("whitegrid", {'grid.linestyle': '--'})
sns.set_context("talk", 1, {"lines.linewidth": 4})
sns.set_palette("GnBu", 11, 0.8)

x = np.arange(-10, 10, 0.1)

fig=plt.figure(figsize=(16,9))
ax = fig.add_subplot(1, 1, 1)
ax.set_title('Normal Distribution (sigma = 1)')
ax.set_ylabel('Probability density')


plots = [
    ax.plot(
        x, norm.pdf(x, loc=mu, scale=1)
    )
    for mu in range(-5, 6,1)
]

ax.legend(['mu: '+str(mu) for mu in range(-5,6,1)])

plt.show()

$\sigma$ を変化させたときの分布の形状

$\sigma$を変化させると分布の裾の長さが変化する

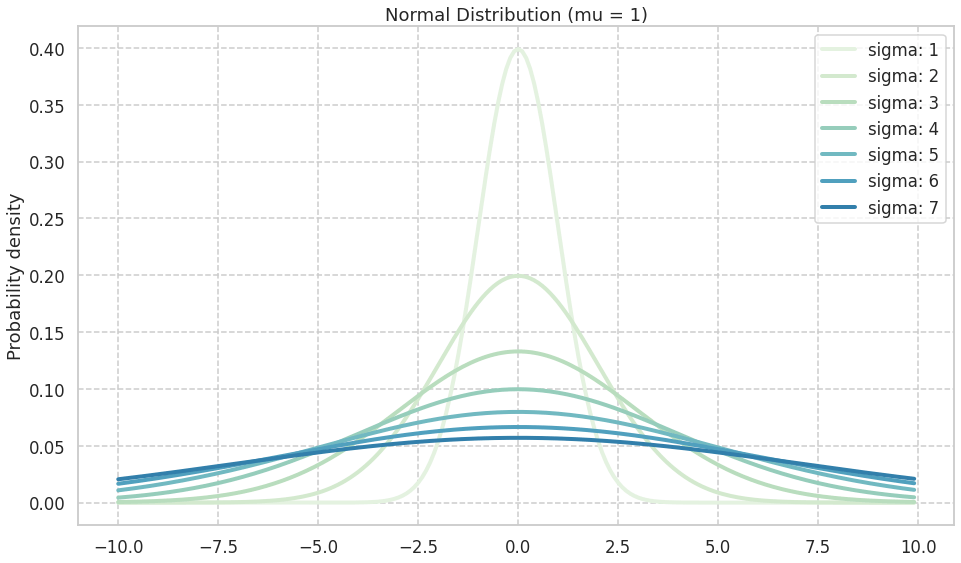
scaleは$\sigma^2$ではなく, $\sigma$なので注意. (参照: scipy: scipy.stats.norm )

以下コード:

1. 初めに必要となるライブラリをimport.($\mu$のときと同じため省略)
2. グラフを描画.

sns.set()
sns.set_style("whitegrid", {'grid.linestyle': '--'})
sns.set_context("talk", 1, {"lines.linewidth": 4})
sns.set_palette("GnBu", 8, 0.8)

x = np.arange(-10, 10, 0.1)

fig=plt.figure(figsize=(16,9))
ax = fig.add_subplot(1, 1, 1)
ax.set_title('Normal Distribution (mu = 1)')
ax.set_ylabel('Probability density')


plots = [
    ax.plot(
        x, norm.pdf(x, loc=0, scale=sigma)
    )
    for sigma in range(1, 8, 1)
]

ax.legend(['sigma: '+str(sigma) for sigma in range(1, 8, 1)])

plt.show()

補足

※1: ガウス分布(Gaussian distribution)とも呼ばれる.
※2: 文献(2)60頁参考.
※3: $\mathbb{E}(e^{tX})$をマクローリン展開することで示すことができる.

参考文献

(1) 竹村彰通.”新装改訂版 現代数理統計学”.2020.学術図書出版社
(2) 一般社団法人 日本統計学会.”日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブック”.2020.学術図書出版社
(3) 一般社団法人 日本統計学会.”日本統計学会公式認定 統計検定1級対応 統計学”.2013.東京図書出版社
(4)C.M.ビショップ.”パターン認識と機械学習 上 ベイズ理論による統計的予測”.2019.丸善出版株式会社
(5)須山敦志.”機械学習スタートアップシリーズ ベイズ推論による機械学習入門”.2018.株式会社講談社サイエンティフィク

参考サイト

(1) matplotlib document
(2) scipy document