[統計学] 二項分布のベイズ推定

二項分布のベイズ推定について, ベータ分布が共役事前分布であるという記載はあったが, 事後分布や予測分布の導出が無かったため導出した. また, パラメータの分布や予測分布の更新をプログラミング言語Pythonを用いて可視化を行った.

共役事前分布と尤度関数

共役事前分布

二項分布の共役事前分布はベータ分布である.

$$Beta(\mu | a, b) = \frac{\Gamma{(a+b)}}{\Gamma{(a)} \Gamma{(b)}} \mu^{a-1} (1-\mu)^{b-1}$$

後程使用するので対数をとった形を記載する. ただし, 正規化項を定数としておいていることに注意.

$$\ln Beta(\mu | a, b) =(a-1)\ln \mu + (b-1) \ln (1-\mu) + \text{const.}$$

ベータ分布の確率密度関数を確認する. 初めに $a+b=10$ に固定しながら $a,b$ の値を変化させる. $a+b$ に占める $a$ の割合が多いほど確率密度関数が右寄りになっていく様子がわかる.

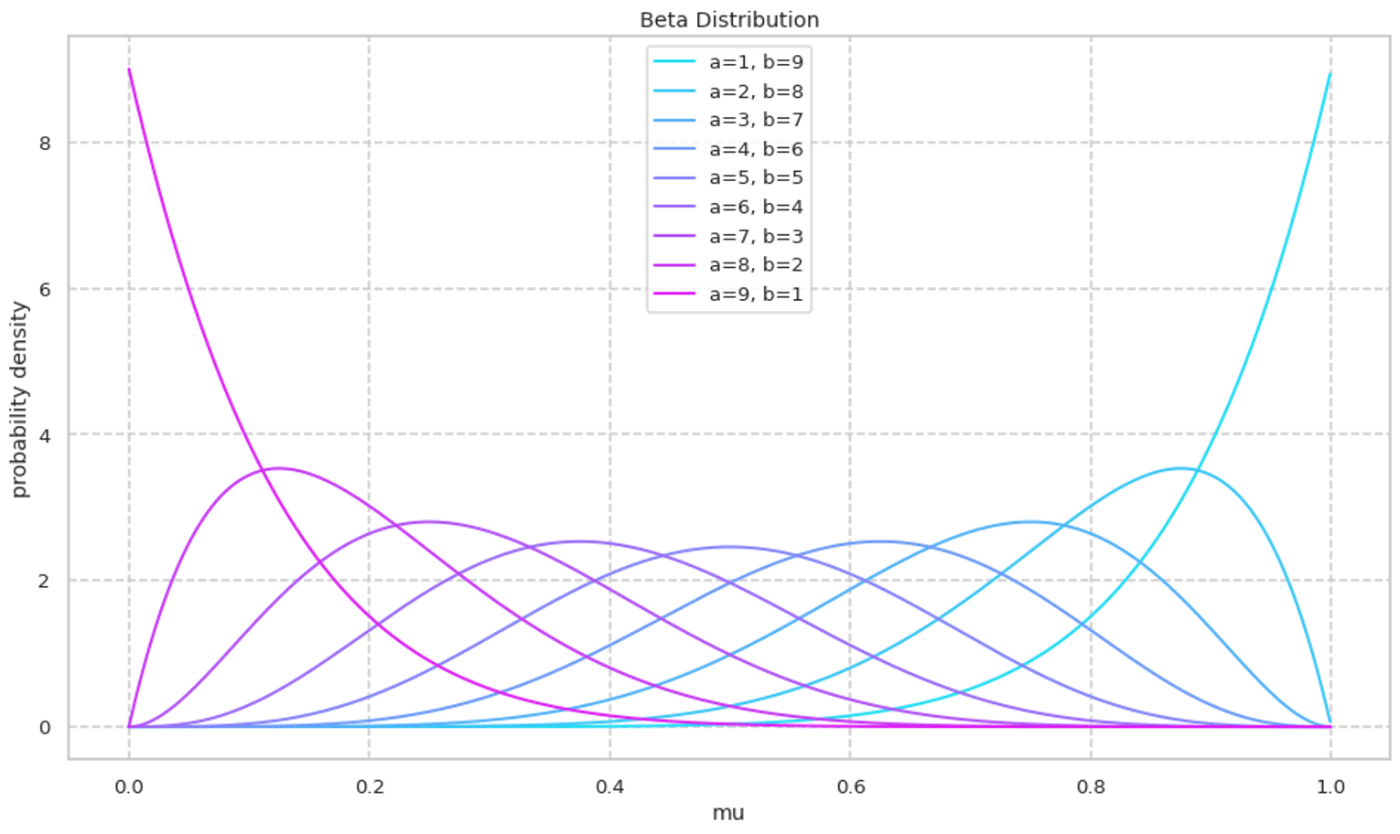
次に $a/b$ を固定しながら $a,b$ の絶対値を大きくしていく様子を可視化する. 絶対値が大きくなるにつれて確率密度が大きくなる様子が確認できる.

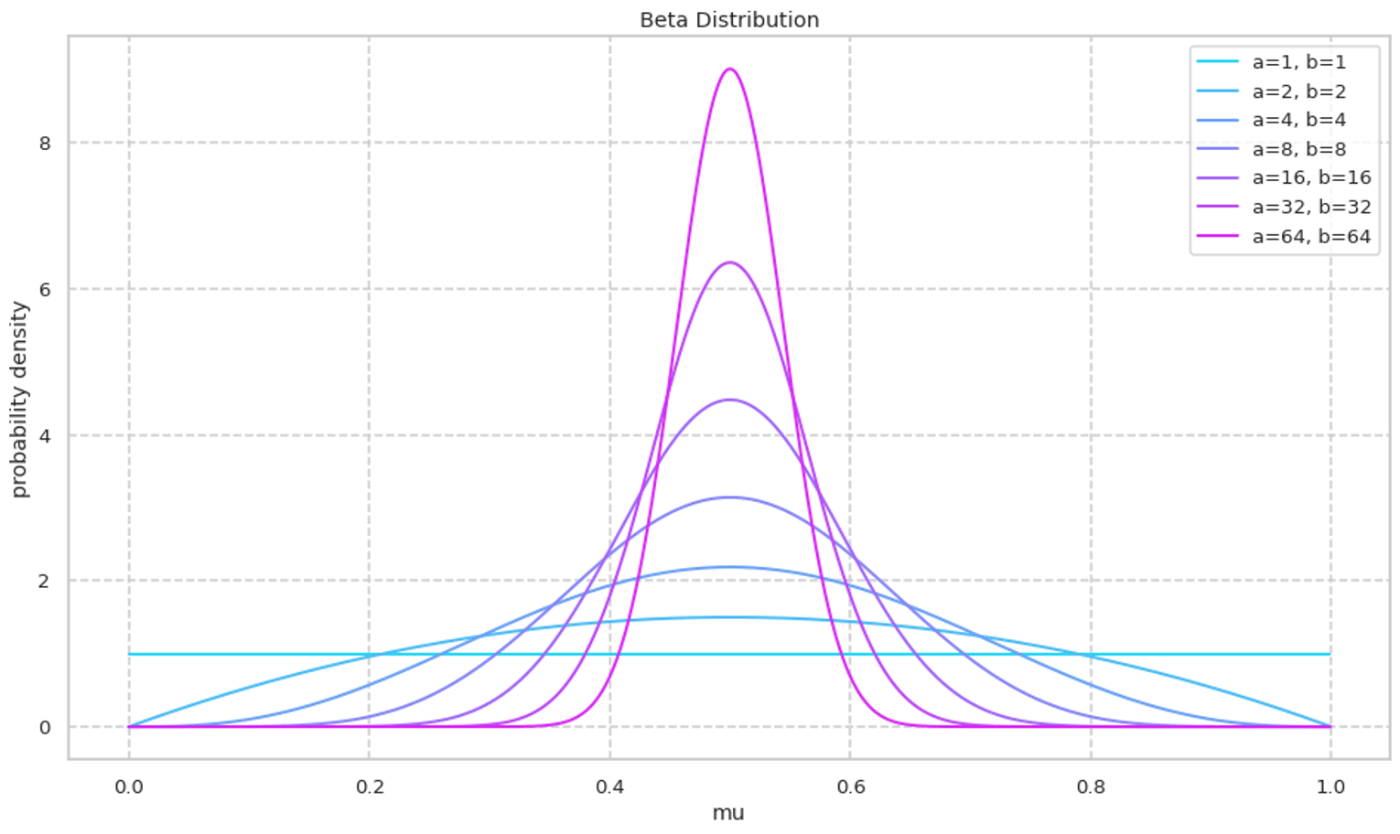
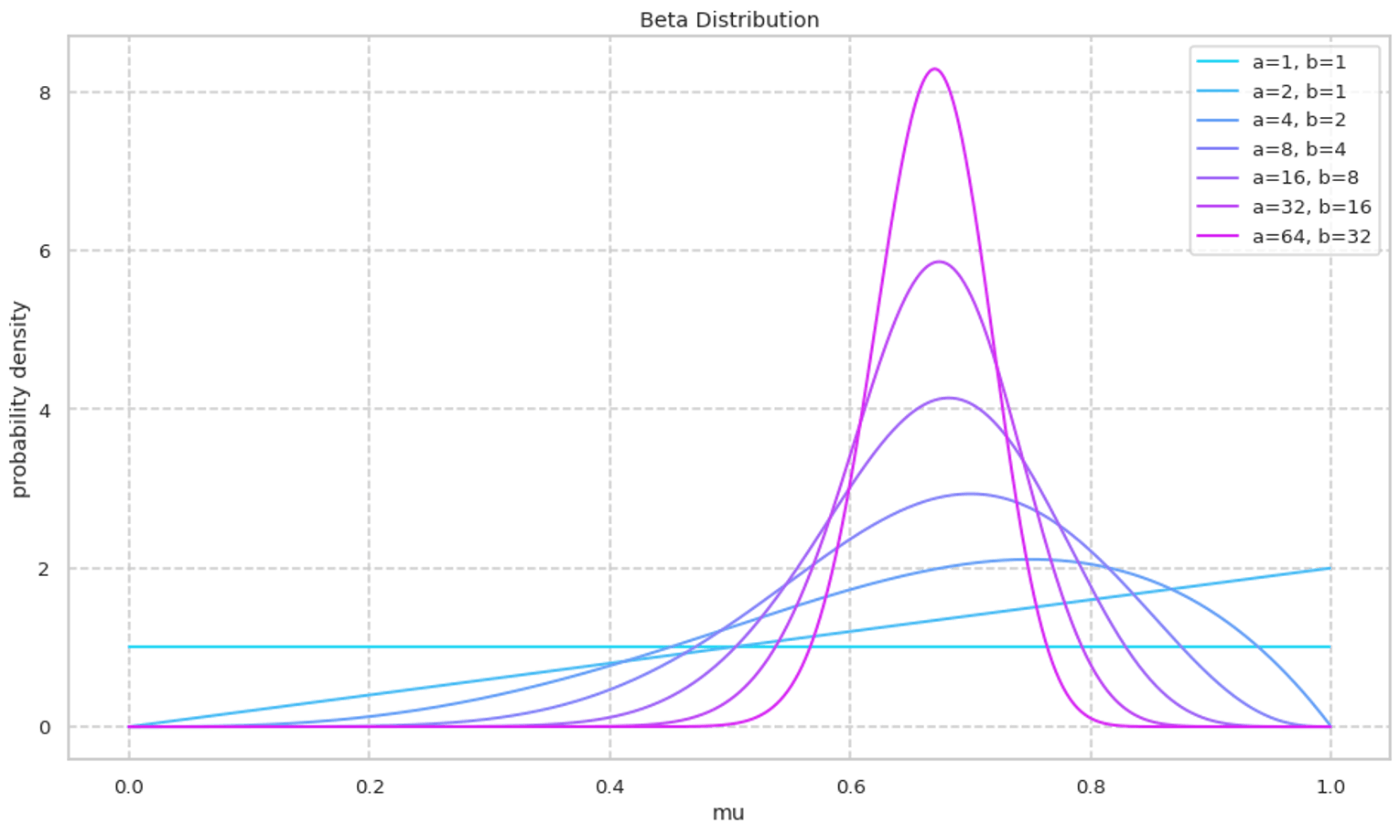
尤度関数に用いる分布

尤度関数に用いる二項分布は以下に示す通りである

$$Bin(x |n, \mu)= \binom{n}{x} \mu^x (1-\mu)^{n-x}$$

確率質量関数を可視化する. 初めに $n$ を固定して $\mu$ を変化させる.

次に $n$ を変化させると期待値と分散が大きくなる.

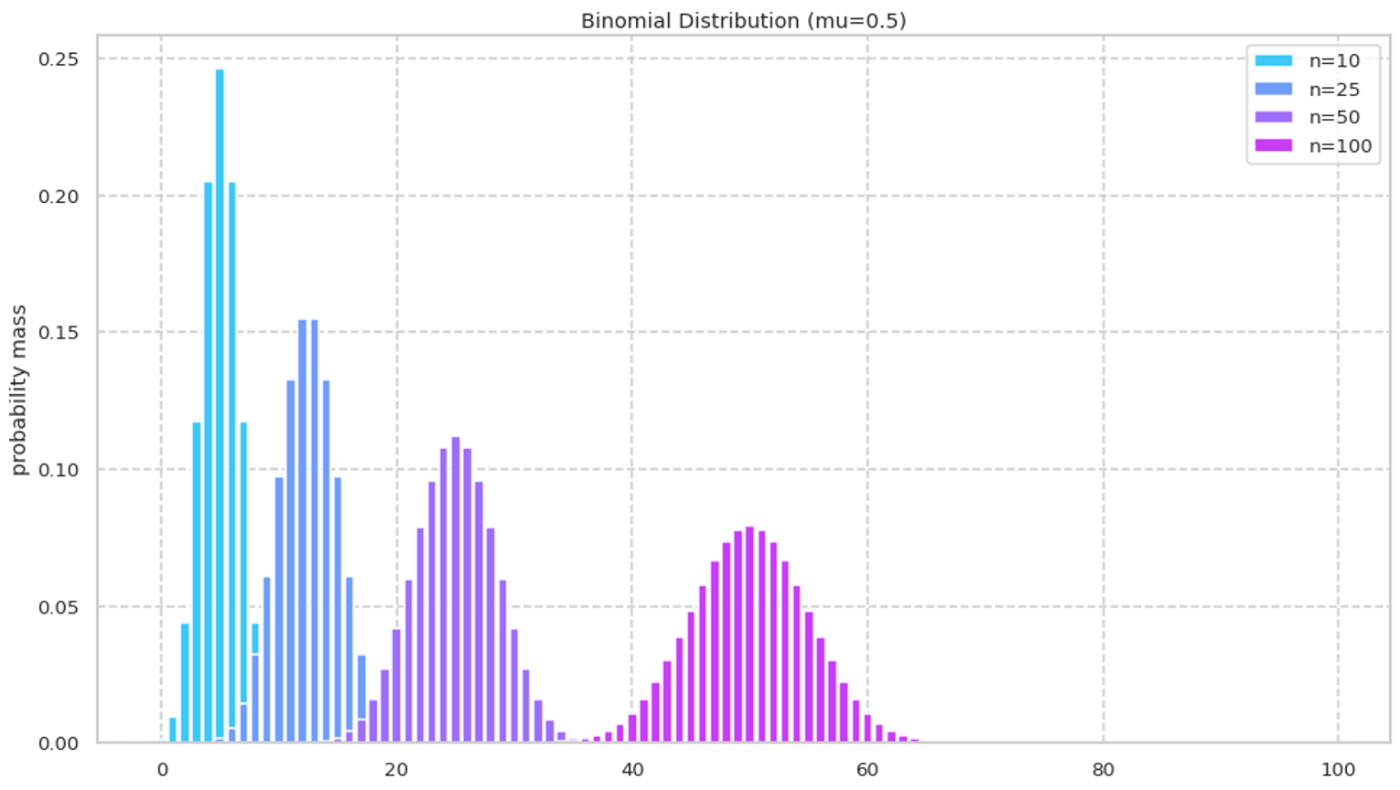
事後分布の導出

データ $\mathbf{x} = \{x_1 \; x_2 \; \cdots x_N \}$ が観測されたと仮定する. このとき, ベイズの定理から,

$$p(\mu | \mathbf{x}) \propto p(\mathbf{x}|\mu)p(\mu)$$

である. ここで対数をとり, パラメータに関係のない項を定数項(以下 $\text{const.}$ と表記) にまとめて計算すると,

$$\begin{align*} \ln p(\mu | \mathbf{x}) &\propto \ln (\mathbf{x|\mu}) + \ln p(\mu) \\ &= \ln \prod_{i=1}^N p(x_i|\mu) + \ln p(\mu) \\ &= \sum_{i=1}^N\ln p(x_i|\mu) + \ln p(\mu) \\ &= \sum_{i=1}^N\ln [\mu^{x_i} \:(1-\mu)^{n-x_i}] + \ln [\mu^{a-1} \:(1-\mu)^{b-1}] + \text{const.} \\ &= (\sum_{i=1}^N x_i) \ln \mu + \sum_{i=1}^N (n-x_i) \ln (1-\mu) + (a-1)\ln \mu + (b-1)\ln(1-\mu) + \text{const.} \\ &= (\sum_{i=1}^N x_i) \ln \mu + (Nn-\sum_{i=1}^Nx_i) \ln (1-\mu) + (a-1)\ln \mu + (b-1)\ln(1-\mu) + \text{const.} \\ &= [(\sum_{i=1}^N x_i)+a-1] \ln \mu + [(Nn-\sum_{i=1}^Nx_i)+b-1] \ln (1-\mu) + \text{const.} \end{align*}$$

5行目は $\sum_1^N n = Nn$ を用いていることに注意する.
導出した式と前述したベータ分布に対数をとった式を見比べることで, 事後分布が以下であることが分かる.

$$\begin{align*} p(\mu|\mathbf{x})&=Beta(a',b') \\ \text{Where,} &\; a'=(\sum_{i=1}^N x_i)+a),\;b'=(Nn-\sum_{i=1}^N x_i)+b) \end{align*}$$

事後分布の可視化

事前分布を以下のように定義する. ただし, ハイパーパラメータはとして, $a=1,b=1$ とする.

$$\begin{align*} & Beta(\mu|a,\;b) \\ a&=1,\;b=1 \end{align*}$$

尤度関数は以下とする.

$$Bin(x | n = 5, \mu)= \binom{5}{x} \mu^x (1-\mu)^{5-x}$$

今, $\mathbf{x}=[3,4,3,5]$ が得られたとする. このとき事後分布は,

$$\begin{align*} p(\mu|\mathbf{x})&=Beta(a',b') \\ \text{Where,} &\; a'=(\{3+4+3+5\}+1),\;b'=(4*5-\{3+4+3+5\})+1) \end{align*}$$

つまり,

$$\begin{align*} p(\mu|\mathbf{x})&=Beta(16,6) \end{align*}$$

ここで事前分布と事後分布を比較すると以下の様になる.

図より, 元々一様だったパラメータの確率密度の分布が左に裾の長い分布に変化していることが分かる.

ちなみに最尤推定量は $\mu_{ML} = \frac{\sum_{i=1}^N x_i}{Nn} = \frac{3}{4}$ である. 最尤推定については以下の記事でまとめているので適宜参照されたい.

二項分布の期待値と分散, 最尤推定, 可視化

予測分布の導出

$p(x_\star)$ を考える. 便宜上, 超パラメータは $a, b$ とおく.

$$\begin{align*} p(x_\star) &= \int p(x_\star|\mu)p(\mu|a,b) \; d\mu \\ &= \int \frac{n!}{x_\star!(n-x!)} \mu^{x_\star} \:(1-\mu)^{n-x_\star} \frac{\Gamma{(a+b)}}{\Gamma{(a)}\Gamma{(b)}} \mu^{a-1} \:(1-\mu)^{b-1} \; d\mu \\ &= \frac{n!}{x_\star!(n-x!)} \frac{\Gamma{(a+b)}}{\Gamma{(a)}\Gamma{(b)}} \int \mu^{x_\star+a-1} \:(1-\mu)^{n-x_\star+b-1} \; d\mu \\ &= \frac{n!}{x_\star!(n-x!)} \frac{\Gamma{(a+b)}}{\Gamma{(a)}\Gamma{(b)}} \frac{\Gamma{(x_\star+a)}\Gamma{(n-x_\star+b)}}{\Gamma{(n+a+b)}} \end{align*}$$

最終行から, 二項分布のパラメータをベータ分布に従うことを仮定すると以下で定義されるベータ二項分布になることが分かる.

$$\begin{align*} f(x) &= \binom{n}{x} \frac{B(x+a,n-x+b)}{B(a, b)} \\ &= \binom{n}{x} \frac{\Gamma{(x+a)} \Gamma{(n-x+b)}}{\Gamma{(n+a+b)}} \frac{\Gamma{(a+b)} }{\Gamma{(a)}\Gamma{(b)}} \\ &= \binom{n}{x} \frac{\Gamma{(a+b)} }{\Gamma{(\alpha)}\Gamma{(b)}} \frac{\Gamma{(x+a)} \Gamma{(n-x+b)}}{\Gamma{(n+a+b)}} \end{align*}$$

ただし, 最終行は以下を用いている.

$$\frac{\Gamma{(a+b)}}{\Gamma{(a)}\Gamma{(b)}} \int \mu^{a-1} \:(1-\mu)^{b-1} \;d\mu=1$$

先ほどの結果を代入すると,

$$\begin{align*} p(x_\star) &= \frac{n!}{x_\star!(n-x_\star!)} \frac{\Gamma{(a'+b')}}{\Gamma{(a')}\Gamma{(b')}} \frac{\Gamma{(x_\star+a')}\Gamma{(n-x_\star+b')}}{\Gamma{(n+a'+b')}} \\ &= \frac{n!}{x_\star!(n-x_\star!)} \frac{\Gamma{(Nn+a+b)}}{\Gamma{(\sum_{i=1}^N x_i+a)}\Gamma{(Nn-\sum_{i=1}^N x_i + b)}} \frac{\Gamma{(x_\star+\sum_{i=1}^N x_i + a)}\Gamma{(n-x_\star + Nn-\sum_{i=1}^N x_i+b)}}{\Gamma{(n+Nn+a+b)}} \end{align*}$$

予測分布の可視化

比較するために, $\mu=0.5$ としたときの二項分布と下記のパラメータを持つベータ二項分布を可視化する.

$$\begin{align*} a= 16, \;b=6, \;n=5 \end{align*}$$

予測分布も左に裾が長い分布であることがわかる.

参考文献

(1) 久保川.2017."現代数理統計学の基礎".共立出版
(2) C.M.ビショップ.”パターン認識と機械学習 上 ベイズ理論による統計的予測”.2019.丸善出版
(3) 須山敦志.”機械学習スタートアップシリーズ ベイズ推論による機械学習入門”.2018.講談社サイエンティフィク
(4) Wikipedia.”Beta-binomial distribution”.2022-11-2 (last edit)