[統計学] ベータ分布の可視化・期待値・分散・最尤推定・ベイズモデル

確率密度関数 (probability density function)

ベータ分布の確率密度関数は以下のように定義される．ただし，$x$の定義行きに注意せよ．

$$\begin{align*} f_{X}(x) &= B(\alpha, \beta)^{-1} x^{\alpha-1} (1-x)^{\beta-1} \\ x &\in [0, 1] \end{align*}$$

可視化

ベータ分布の確率密度関数を確認する. 初めに $a+b=10$ に固定しながら $a,b$ の値を変化させる.

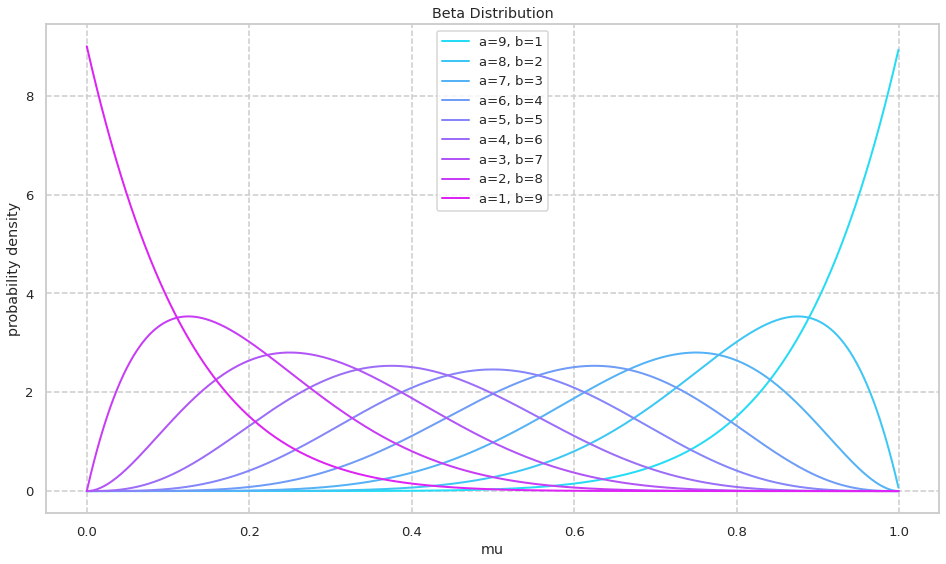
次に a/b を固定しながら $a,b$ の絶対値を大きくしていく様子を可視化する. $a,b$ の絶対値が大きくなるにつれて峰の確率密度が大きくなる様子が確認できる.

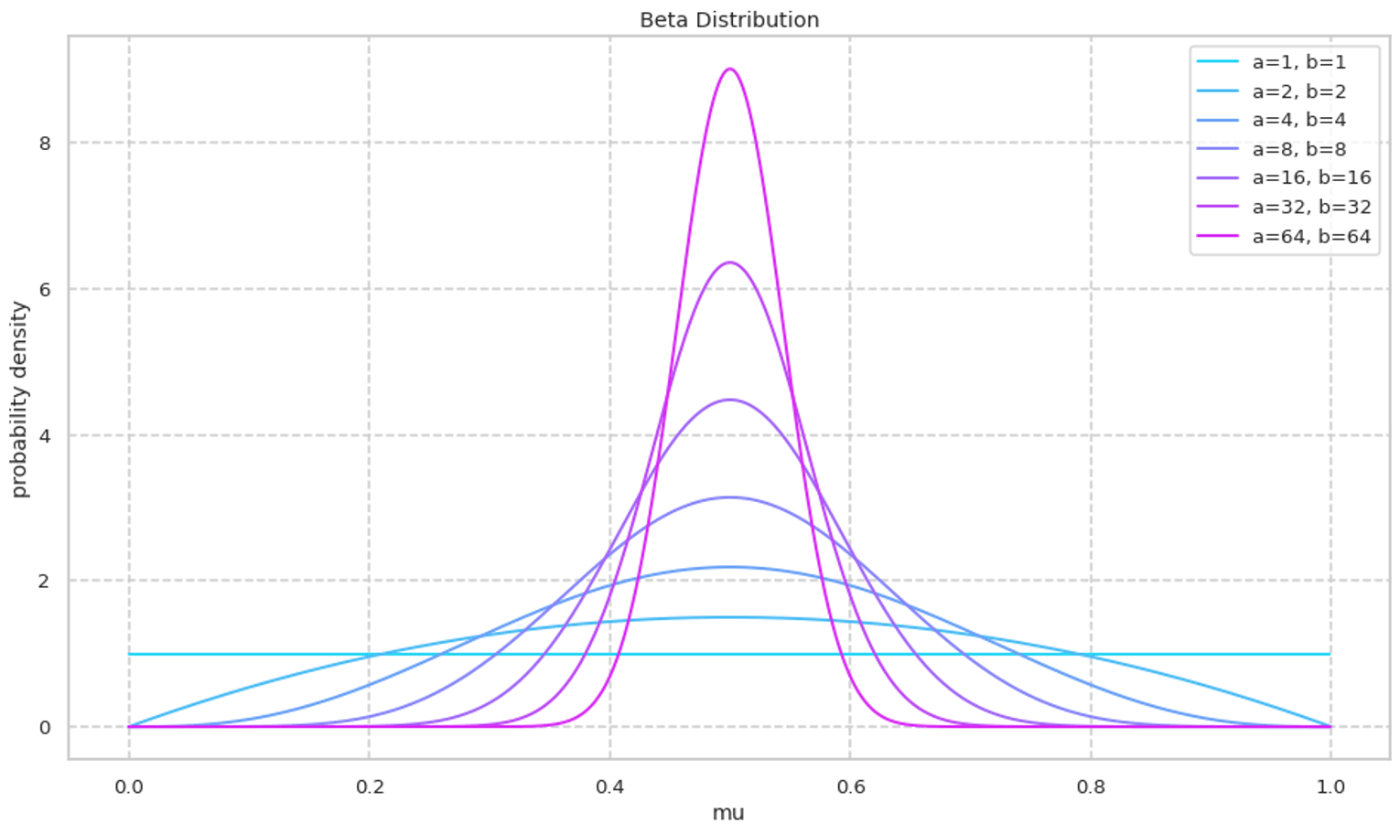
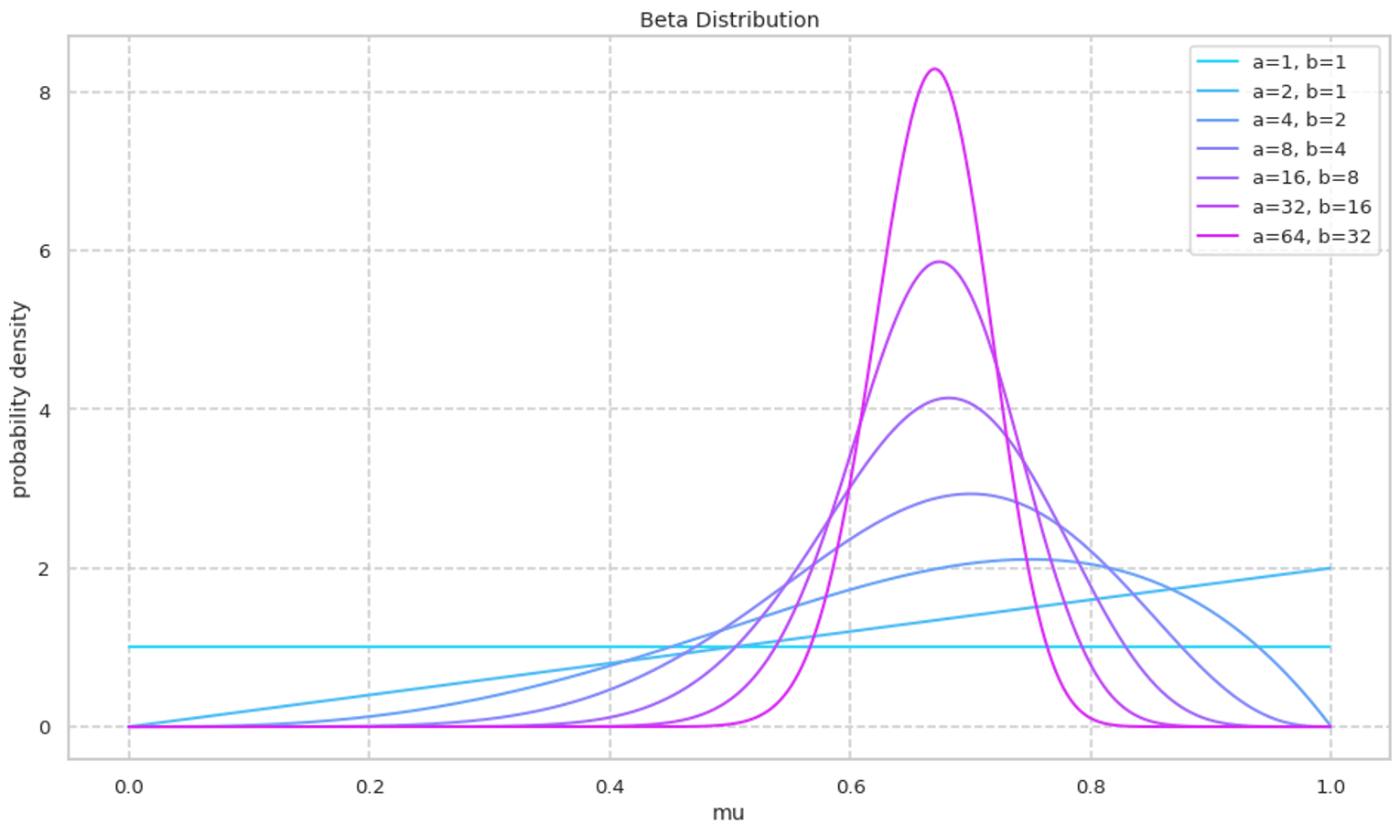
以下はグラフを生成するコードである．
3枚あるが, 差分は変数 a_b と ax.legend([...]) のみなので1枚目のみを掲載する.

上記の写真を生成するコード

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import beta

a_b = [
    [9,1],
    [8,2],
    [7,3],
    [6,4],
    [5,5],
    [4,6],
    [3,7],
    [2,8],
    [1,9],
]

# data
x = np.arange(0, 1, 0.001)
ys = []
for ab in a_b:
    y = [beta.pdf(x_i, ab[0], ab[1])for x_i in x]
    ys.append(y)

sns.set()
sns.set_style("whitegrid", {'grid.linestyle': '--'})
sns.set_context("talk", 0.8, {"lines.linewidth": 2})
sns.set_palette("cool", 9, 0.9)

fig=plt.figure(figsize=(16,9))
ax1 = fig.add_subplot(1, 1, 1)
ax1.set_title('Beta Distribution')
ax1.set_xlabel('mu')
ax1.set_ylabel('probability density')

for ys_i in ys:
    ax1.plot(x,ys_i)

ax1.legend([
    'a=9, b=1',
    'a=8, b=2',
    'a=7, b=3',
    'a=6, b=4',
    'a=5, b=5',
    'a=4, b=6',
    'a=3, b=7',
    'a=2, b=8',
    'a=1, b=9',
])
plt.show()

ベータ関数とガンマ関数の関係

本記事で多用するため，式変形とその導出を載せる.

等式

$$B(\alpha, \beta)=\frac{\Gamma(\alpha) \Gamma(\beta)}{\Gamma(\alpha+\beta)}$$

導出

$$\begin{align*} & \Gamma(z) = \int_{0}^{\infty} t^{z-1} e^{-t} \, dt \\ & B(\alpha, \beta) = \int_{0}^{1} t^{\alpha-1} (1-t)^{\beta-1} \, dt \\ \end{align*}$$

$\Gamma(\alpha) \Gamma(\beta)$ を変形して，ベータ関数とガンマ関数の掛け算の式に変形する．

$$\begin{align*} \Gamma(\alpha) \Gamma(\beta) &= \int_{0}^{\infty} \int_{0}^{\infty} s^{\alpha-1} e^{-s} \, ds \, t^{\beta-1} e^{-t} \, dt \\ & = \int_{0}^{\infty} \int_{0}^{\infty} s^{\alpha-1} t^{\beta-1} e^{-(s+t)} \, ds \, dt \\ & = f(s, t) \\ \end{align*}$$

ここで2変数の変数変換を行う．

$$\begin{align*} & \begin{cases} { s = uv } \\ { t = u(1-v) } \end{cases} \Leftrightarrow \begin{cases} u = s+t \\ v = s(s+t)^{-1} \end{cases} \\ & t, s: 0 \rightarrow \infty, \ u: 0 \rightarrow \infty, \ v: 0 \rightarrow 1 \end{align*}$$

よって，

$$\begin{align*} f(u, v) &= f(s, t) \left| J((u, v) \rightarrow (s, t)) \right| \\ & = f(uv, u(1-v)) \left| \operatorname{det}\left(\begin{array}{cc} v & u \\ (1-v) & -u \end{array}\right) \right| \\ & = f(uv, u(1-v)) \cdot u \\ & = \int_{0}^{\infty} \int_{0}^{1} (uv)^{\alpha-1} \{u(1-v)\}^{\beta-1} e^{-u} u \, du \, dv \\ & = \int_{0}^{\infty} \int_{0}^{1} u^{\alpha+\beta-1} v^{\alpha-1} (1-v)^{\beta-1} e^{-u} \, du \, dv \\ & = \int_{0}^{\infty} u^{\alpha+\beta-1} e^{-u} \, du \int_{0}^{1} v^{\alpha-1} (1-v)^{\beta-1} \, dv \\ & = \Gamma(\alpha+\beta) B(\alpha, \beta) \end{align*}$$

上記の式を整理すれば，求める等式を得られる．

$$B(\alpha, \beta)=\frac{\Gamma(\alpha) \Gamma(\beta)}{\Gamma(\alpha+\beta)}$$

期待値と分散 (Expected Value and Variance)

期待値

$$\begin{align*} \mathbb{E}(X) &= \int_{0}^{1} x f_{X}(x) \, dx \\ &= \int_{0}^{1} x \beta(\alpha, \beta)^{-1} x^{\alpha-1}(1-x)^{\beta-1} \, dx \\ &= B(\alpha, \beta)^{-1} \int_{0}^{1} x^{\alpha}(1-x)^{\beta-1} \, dx \\ &= B(\alpha, \beta)^{-1} B(\alpha+1, \beta) \\ &= \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)} \cdot \frac{\Gamma(\alpha+1)\Gamma(\beta)}{\Gamma(\alpha+\beta+1)} \\ &= \frac{\Gamma(\alpha+\beta) \alpha \Gamma(\alpha)}{\Gamma(\alpha)(\alpha+\beta) \Gamma(\alpha+\beta)} \\ &= \frac{\alpha}{\alpha+\beta} \end{align*}$$

分散

先に$\mathbb{E}(X^2)$を求め， $\mathbb{V}(X)=\mathbb{E}(X^2)-\mathbb{E}(X)^2$ を使って導出する．

$$\begin{align*} E\left(X^{2}\right) &= \int_{0}^{1} x^{2} f_{X}(x) \, dx \\ &= \int_{0}^{1} x^{2} B(\alpha, \beta)^{-1} x^{\alpha-1}(1-x)^{\beta-1} \, dx \\ &= B(\alpha, \beta)^{-1} \int_{0}^{1} x^{\alpha+1}(1-x)^{\beta-1} \, dx \\ &= B(\alpha, \beta)^{-1} B(\alpha+2, \beta) \\ &= \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)} \cdot \frac{\Gamma(\alpha+2)\Gamma(\beta)}{\Gamma(\alpha+\beta+2)} \\ &= \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)} \cdot \frac{(\alpha+1)\alpha \Gamma(\alpha)}{(\alpha+\beta+1)(\alpha+\beta)\Gamma(\alpha+\beta)} \\ &= \frac{\alpha(\alpha+1)}{(\alpha+\beta)(\alpha+\beta+1)} \end{align*}$$

前述した期待値と合わせて計算する．

$$\begin{align*} V(X) &= \frac{\alpha(\alpha+1)}{(\alpha+\beta)(\alpha+\beta+1)} - \left(\frac{\alpha}{\alpha+\beta}\right)^{2} \\ &= (\alpha+\beta)^{-2}(\alpha+\beta+1)^{-1} \left\{\alpha(\alpha+1)(\alpha+\beta) - \alpha^{2}(\alpha+\beta+1)\right\} \\ & = \alpha(\alpha+\beta)^{-2}(\alpha+\beta+1)^{-1}\left\{\alpha^{2}+\alpha \beta+\alpha+\beta-\alpha^{2}-\alpha \beta-\alpha\right\} \\ & =\alpha \beta(\alpha+\beta)^{-2}(\alpha+\beta+1)^{-1} \end{align*}$$

最尤推定 (Maximum Likelihood Estimation)

以下を仮定する．

$$\begin{align*} & \{X_i\}_{i=1}^{n}, \text{ i.i.d. } \sim \operatorname{Beta}(\alpha, \beta) \\ \end{align*}$$

尤度関数と対数尤度関数を求める．

$$\begin{align*} L(\alpha, \beta) & = f\left(x_{1}, x_{2}, \ldots, x_{n}\right) \\ & = \prod_{i=1}^{n} f\left(x_{i}\right) \\ & = \prod_{i=1}^{n} B(\alpha, \beta)^{-1} x_{i}^{\alpha-1} \left(1-x_{i}\right)^{\beta-1} \\ & = B(\alpha, \beta)^{-n} \prod_{i=1}^{n} x_{i}^{\alpha-1} \left(1-x_{i}\right)^{\beta-1} \\ \log L(\alpha, \beta) &= -n \log B(\alpha, \beta) + (\alpha-1) \sum_{i=1}^{n} \log x_{i} + (\beta-1) \sum_{i=1}^{n} \log \left(1-x_{i}\right) \end{align*}$$

解析的に解く場合，上記の式を解きたいパラメータについて偏微分して求める．しかし，前述した通り，Beta関数はガンマ関数で構成されていて計算が複雑になる．実践としては数値計算で求めることが多い．

ベータ分布を用いたベイズ推定 (Beta-Bernolli Model)

ベータ分布はベルヌーイ分布の共役事前分布であるのでよく用いられる．

$$\begin{align*} & X \sim \operatorname{Bern}(\mu), \quad f_{x}(x) = \mu^{x}(1-\mu)^{1-x} \\ & \mu \sim \operatorname{Beta}(\alpha, \beta), \quad f_{\mu}(\mu) = B(\alpha, \beta)^{-1} \mu^{\alpha-1}(1-\mu)^{\beta-1} \\ \end{align*}$$

事後分布の導出

事後分布(posterior-distribution)を導出する前に，ベルヌーイ分布の対数尤度関数を計算しておく．以下を仮定する．

$$\{X_i\}_{i=1}^{n}, \text{ i.i.d. } \sim \operatorname{Bern}(\mu) \\$$

このとき，対数尤度関数は，以下のように計算される．

$$\begin{align*} \log f(x) & = \log f\left(x_{1}, x_{2}, \ldots, x_{n}\right) \\ & = \log \prod_{i=1}^{n} f\left(x_{i}\right) \\ & = \log \prod_{i=1}^{n} \mu^{x_{i}}(1-\mu)^{1-x_{i}} \\ & = \sum_{i=1}^{n} \left\{ x_{i} \log \mu + \left(1-x_{i}\right) \log (1-\mu) \right\} \\ & = \sum_{i=1}^{n} x_{i} \log \mu + \left(n-\sum_{i=1}^{n} x_{i}\right) \log (1-\mu) \\ \end{align*}$$

よって，対数事後分布は以下のように求まる．

$$\begin{align*} \log f(\mu \mid x) & \propto \log \left( f(x \mid \mu) f(\mu) \right) \\ & = \log f(x \mid \mu) + \log f(\mu) \\ & = \sum_{i=1}^{n} x_{i} \log \mu + \left(n-\sum_{i=1}^{n} x_{i}\right) \log (1-\mu) \\ & + \log B(\alpha, \beta)^{-1} + (\alpha-1) \log \mu + (\beta-1) \log (1-\mu) \\ & \propto \left(\alpha+\sum_{i=1}^{n} x_{i}-1\right) \log \mu + \left(\beta+\left\{n-\sum_{i=1}^{n} x_{i}\right\}-1\right) \log (1-\mu) \end{align*}$$

事後分布は，以下である．

$$\mu \sim \operatorname{Beta}\left(\alpha+\sum x_{i}, \beta+n-\sum x_{i}\right)$$

予測分布の導出

予測分布を求める．

$$\begin{align*} f\left(x_{*} \mid \alpha^{\prime}, \beta^{\prime}, \mathbf{x} \right) & = \int_{0}^{1} f\left(x_{*} \mid \mu\right) f\left(\mu \mid \alpha^{\prime}, \beta^{\prime}\right) d \mu \\ & = \int \mu^{x_{*}}(1-\mu)^{1-x_{*}} B\left(\alpha^{\prime}, \beta^{\prime}\right)^{-1} \mu^{\alpha^{\prime}-1}(1-\mu)^{\beta^{\prime}-1} d \mu \\ & = \int B\left(\alpha^{\prime}, \beta^{\prime}\right)^{-1} \mu^{\alpha^{\prime}+x_{*}-1}(1-\mu)^{\beta^{\prime}+\left(1-x_{*}\right)-1} d \mu \\ & = B\left(\alpha^{\prime}, \beta^{\prime}\right)^{-1} B\left(\alpha^{\prime}+x_{*}, \beta^{\prime}+\left(1-x_{*}\right)\right) \end{align*}$$

ところで，$x \in \{0, 1\}$ であるから，

$$\begin{align*} & p\left(x_{*}=1 \mid \mu, x\right) = \frac{\Gamma\left(\alpha^{\prime}+\beta^{\prime}\right)}{\Gamma\left(\alpha^{\prime}\right) \Gamma\left(\beta^{\prime}\right)} \cdot \frac{\Gamma\left(\alpha^{\prime}+1\right) \Gamma\left(\beta^{\prime}\right)}{\Gamma\left(\alpha^{\prime}+\beta^{\prime}+1\right)} \\ & = \frac{\Gamma\left(\alpha^{\prime}+\beta^{\prime}\right)}{\Gamma\left(\alpha^{\prime}\right) \Gamma\left(\beta^{\prime}\right)} \cdot \frac{\alpha^{\prime} \Gamma\left(\alpha^{\prime}\right) \Gamma\left(\beta^{\prime}\right)}{\left(\alpha^{\prime}+\beta^{\prime}\right) \Gamma\left(\alpha^{\prime}+\beta^{\prime}+1\right)} \\ & = \frac{\alpha^{\prime}}{\alpha^{\prime}+\beta^{\prime}} \\ \end{align*}$$

$$\begin{align*} X_{*} \mid \mu, X, \alpha, \beta \sim \operatorname{Bern}\left(\frac{\alpha^{\prime}}{\alpha^{\prime}+\beta^{\prime}}\right) = \operatorname{Bern}\left(\frac{\alpha+\sum x_{i}}{\alpha+\beta+n}\right) \end{align*}$$

ベータ分布を用いたベイズ推定 (Beta-Binomial Model)

ベルヌーイ分布の多試行版である，二項分布の共役事前分布もまた，ベータ分布である．

$$\begin{align*} & X \sim \operatorname{Bin}(n, \mu), \quad f_{x}(x) = \binom{n}{x} \mu^{x}(1-\mu)^{n-x} \\ & \mu \sim \operatorname{Beta}(\alpha, \beta), \quad f_{\mu}(\mu) = B(\alpha, \beta)^{-1} \mu^{\alpha-1}(1-\mu)^{\beta-1} \end{align*}$$

事後分布の導出

ベルヌーイ分布と同様に事後分布を求める．

$$\begin{align*} \log f(\mu \mid x) & \propto \log f(x \mid \mu)+\log f(\mu) \\ & \propto \log \Pi_{i=1}^{N} \mu^{x_{i}}(1-\mu)^{n-x_{i}}+\log \mu^{\alpha-1}(1-\mu)^{\beta-1} \\ & = \sum_{i=1}^{N} \log \mu^{x_{i}}(1-\mu)^{n-x_{i}}+\log \mu^{\alpha-1}(1-\mu)^{p_{p}-1} \\ & = \sum x_{i} \log \mu+\sum\left(n-x_{i}\right) \log (1-\mu)+(\alpha-1) \log \mu+(\beta-1) \log (1-\mu) \\ & = \sum x_{i} \log \mu+\left(Nn-\sum x_{i}\right) \log (1-\mu)+(\alpha-1) \log \mu+(\beta-1) \log (1-\mu) \\ & = \left(\alpha+\sum x_{i}-1\right) \log \mu+\left(\beta+Nn-\sum x_{i}-1\right) \log \left(1-\mu_{\mu}\right) \end{align*}$$

以上より，事後分布が以下あることがわかる．

$$\mu \mid \mathbf{X} \sim \operatorname{Beta}\left(\alpha+\sum x_{i}, \beta+Nn-\sum x_{i}\right) \\$$

予測分布の導出，　予測分布の期待値・分散の導出

予測分布は以下である．

$$\begin{align*} f\left(x_{*} \mid \alpha^{\prime}, \beta^{\prime}\right) & = \int_{0}^{1} f\left(\mu \mid \alpha^{\prime}, \beta^{\prime}\right) f\left(x_{*} \mid \mu\right) d \mu \\ & = \binom{n}{x_{*}} B\left(\alpha^{\prime}, \beta^{\prime}\right)^{-1} \int_{0}^{1} \mu^{\alpha^{\prime}+x_{*}-1}(1-\mu)^{\beta+n-x_{*}-1} d \mu \\ & = \binom{n}{x_{*}} B\left(\alpha^{\prime}, \beta^{\prime}\right)^{-1} B\left(\alpha^{\prime}+x_{*}, \beta^{\prime}+n-x_{*}\right) \end{align*}$$

この分布は，ベータ二項分布(Beta-Binomial distribution)と呼ばれる分布である．

この分布の期待値と分散を求める．p.d.f.が複雑であるため，モデルの構造を利用して計算を楽にする．ここまでで文字を使いすぎたので，再度，構造を定義する．

$$X_{*} \mid \mu \sim \operatorname{Bin}(n, \mu), \; \mu \sim \operatorname{Beta}(\alpha, \beta) \\$$

条件付き分布の公式を用いる．

$$\begin{aligned} \mathbb{E}_{X}[X] & = \mathbb{E}_{Y}\left[\mathbb{E}_{X \mid Y}[X | Y]\right] \\ \mathbb{V}_{X}[X] & = \mathbb{E}_{Y}\left[\mathbb{V}_{X \mid Y}[X | Y]\right] + \mathbb{V}_{Y}\left[\mathbb{E}_{X \mid Y}[X | Y]\right] \end{aligned}$$

なお，証明は以下の記事を参照してほしい．

https://zenn.dev/shundeveloper/articles/041c6d6085f22a

公式を用いて変形を行うと，期待値が容易に得られる．

$$\begin{align*} \mathbb{E}\left(X_{*}\right) & = \mathbb{E}_{\mu}\left(\mathbb{E}_{X_{*} \mid \mu}\left(X_{*}\right)\right) \\ & = \mathbb{E}_{\mu}\left(n \mu\right) \\ & = n \mathbb{E}_{\mu}(\mu) \\ & = \frac{n \alpha}{\alpha+\beta} \end{align*}$$

分散を計算するには$\mathbb{E}(X^2)$を上記の方法で求めるのが早い．本記事では，解説のため，敢えて条件付き分散の公式を用いている．

$$\begin{align*} \mathbb{V}\left(X_{*}\right) &= \mathbb{E}\left(X_{*}^{2}\right) - \mathbb{E}\left(X_{*}\right)^{2} \\ &= \mathbb{E}_{\mu}\left[\mathbb{E}_{X_{*} \mid \mu}\left(X_{*}^{2} \mid \mu\right)\right] - \mathbb{E}_{\mu}\left[\mathbb{E}_{X_{*} \mid \mu}\left(X_{*} \mid \mu\right)\right]^{2} \\ &= \mathbb{E}_{\mu}\left[V_{X_{*} \mid \mu}\left(X_{*} \mid \mu\right) + \mathbb{E}_{X_{*} \mid \mu}\left(X_{*} \mid \mu\right)^{2}\right] - \mathbb{E}_{\mu}\left[\mathbb{E}_{X_{*} \mid \mu}\left(X_{*} \mid \mu\right)\right]^{2} & = \mathbb{E}_{\mu}\left[V_{x_{*} \mid \mu}\left(x_{*} \mid \mu\right)\right]+\mathbb{V}_{\mu}\left[\mathbb{E}_{x_{k} \mid \mu}\left(X_{*} \mid \mu\right)\right] \\ & = \mathbb{E}_{\mu}[n \mu(1-\mu)]+V_{\mu}(n \mu) \\ & = n \mathbb{E}_{\mu}(\mu) - n \mathbb{E}\left(\mu^{2}\right)+n^{2} V_{\mu}(\mu) \\ & = n \alpha(\alpha+\beta)^{-1} - n \alpha(\alpha-1)(\alpha+\beta)^{-1}(\alpha+\beta+1)^{-1}+n^{2} \alpha \beta(\alpha+\beta)^{-2}(\alpha+\beta+1)^{-1} \end{align*}$$

本記事では，導出のみを扱ったが，下記の記事において具体例を紹介している．

https://zenn.dev/shundeveloper/articles/986899a7a29e2d

参考文献

(1) 久保川."現代数理統計学の基礎".2017.共立出版
(1) C.M.ビショップ.”パターン認識と機械学習 上 ベイズ理論による統計的予測”.2019.丸善出版
(2) 須山敦志.”機械学習スタートアップシリーズ ベイズ推論による機械学習入門”.2018.講談社サイエンティフィク
(3) Wikipedia.”Beta-binomial distribution”.2022-11-2 (last edit)

更新

• 2024.09.02: 誤字 $\Gamma$ が $P$ になっている箇所を修正