🚀
Box-Muller変換の証明とシュミレーション

2024/08/09に公開
 Box-Muller変換はじめに以下の確率変数を定義する.

\begin{align*}
& U_{1}, U_{2}, \text { i.i.d. } \sim U(0,1)
\end{align*}
以下の確率変数変換を考える．

\begin{align*}
X &= R\cos(\Theta) = (-2\log U_1) \cos(2\pi U_2)\\
Y &= R\sin(\Theta) = (-2\log U_1) \sin(2\pi U_2) 
\end{align*} 
このとき，以下が成り立つ．

\begin{align*}
X, Y, \text { i.i.d. } \sim N(0,1)
\end{align*}

 証明はじめに以下の確率変数を定義する.

\begin{align*}
& U_{1}, U_{2}, \text { i.i.d. } \sim U(0,1)
\end{align*}
この確率変数について，以下の変数変換を考える.

\begin{align*}
\left\{
    \begin{array}{l}
    R = (-2\log U_1)^{-\frac{1}{2}} \\
    \theta = 2\pi U_2
    \end{array}
\right .
\end{align*}
逆変換は以下である．

\begin{align*}
\left\{
    \begin{array}{l}
    U_1 = \exp({-\frac{R^2}{2}}) \\
    U_2 = \frac{\theta}{2\pi}
    \end{array}
\right .
\end{align*}
ここで，ヤコビアンは以下のように計算される.

\begin{align*}
J((r, \theta) \rightarrow (u_1, u_2))
&=\operatorname{det}\left(\begin{array}{cc}
- r e^{-\frac{r^{2}}{2}} & 0 \\
0 & (2 \pi)^{-1}
\end{array}\right) \\
& = -(2 \pi)^{-1} r e^{-\frac{r^{2}}{2}} \cdot 1 \\ 
& = -(2 \pi)^{-1} r e^{-\frac{r^{2}}{2}} \\
\end{align*}
U(0,1)の密度が範囲内で1であることに注意して変形を行う．

\begin{align*}
f_{R \theta}(r, \theta)
&=f_{U_{1} U_{2}}\left(u_{1}, u_{2}\right)\left|J\left(\left(r, \theta\right) \rightarrow(u_1, u_2)\right)\right| \\
& =\frac{r e^{-\frac{r^{2}}{2}}}{2 \pi} \\
\end{align*}
これで，R, \Thetaの同時分布が求まった．

次に，曲座標変換を用いる.

\begin{align*}
& \left\{
    \begin{array}{l}
    X=R \cos \theta \\
    Y=R \sin \theta
    \end{array}
\right .
\end{align*}
ここで，R, \Thetaの逆変換を求めるのは容易ではない．そこで，以下の公式を使う.

J((x, y) \rightarrow(r, \theta))
=
\frac{1}{J((r, \theta) \rightarrow(x, y))}
上式を用いると，ヤコビアンを計算できる．

\begin{align*}
J((x, y) \rightarrow(r, \theta))
&= J((r,\theta) \rightarrow (x,y))^{-1} \\
&= \operatorname{det}\left(\begin{array}{lr}
\cos \theta & -r \sin \theta \\
\sin \theta & r \cos \theta
\end{array}\right)^{-1} \\
&=r^{-1}
\end{align*}
よって求めるX, Yの分布は以下のように定まる．

\begin{align*}
f_{X Y}(x, y)
&=f_{R \theta}(r, \theta)|J((x, y) \rightarrow(r, \theta))| \\
& =\frac{r e^{-\frac{r^{2}}{2}}}{2 \pi} \cdot r^{-1} \\
& =\frac{1}{2 \pi} e^{-\frac{x^{2}+y^{2}}{2}} \\
& =\frac{1}{\sqrt{2 \pi}} e^{-\frac{x^{2}}{2}} \cdot \frac{1}{\sqrt{2 \pi}} e^{-\frac{y^{2}}{2}} \\
&= f_X(x) f_Y(y)
\end{align*}
したがって、XとYはそれぞれ独立に標準正規分布に従う．

 シュミレーション実際にこの変換がうまくいくのか検証を行う．

 プログラムを作成する描画する部分以外は標準関数とmath mouduleのみで動く．実装に際して，generate_samples(n: int)でn // 2を行なっているが，これは，Box-Muller変換が一度に二つの確率変数を生成するためである．
from typing import Tuple

import random
import math
import matplotlib.pyplot as plt
import seaborn as sns


def generate_uniform_random_pair() -> Tuple[float, float]:
    """ 独立に一様分布に従う2つの乱数を生成する。 """
    u1 = random.random()
    u2 = random.random()
    return u1, u2

def box_muller_transform(u1: float, u2: float) -> Tuple[float, float]:
    """ Box-Muller 変換を使用して、独立に一様分布に従う2つの乱数を正規分布に確率変数変換する。 """
    z0 = math.sqrt(-2.0 * math.log(u1)) * math.cos(2.0 * math.pi * u2)
    z1 = math.sqrt(-2.0 * math.log(u1)) * math.sin(2.0 * math.pi * u2)
    return z0, z1

def generate_samples(n: int):
    """ n 個の正規分布に変換された乱数を生成する。 """
    samples = []
    for _ in range(n // 2):
        u1, u2 = generate_uniform_random_pair()
        z0, z1 = box_muller_transform(u1, u2)
        samples.append(z0)
        samples.append(z1)
    return samples[:n]

# Seaborn and Matplotlibの準備
sns.set()
sns.set_style("whitegrid", {'grid.linestyle': '--'})
sns.set_context("talk", 0.8, {"lines.linewidth": 0})
colors = sns.color_palette("cool", 5)

# サンプルサイズを指定
sample_sizes = [10, 50, 100, 1000, 10000]

# それぞれのサイズでシュミレーションを行い, 結果を描画する
for i, n in enumerate(sample_sizes):
    samples = generate_samples(n)
    plt.figure(figsize=(10, 6))  # Fixed size for all figures
    sns.histplot(samples, kde=True, color=colors[i], binwidth=0.5)
    plt.title(f'Box-Muller Transformed Samples for n={n}')
    plt.xlabel('Value')
    plt.ylabel('Frequency')
    plt.show()

 結果nのオーダーがn=10^3ぐらいからは正規分布のように見える．変数変換であって，近似ではないのでサンプルサイズが小さい時も機能すると考えていたがそうでもないらしい．

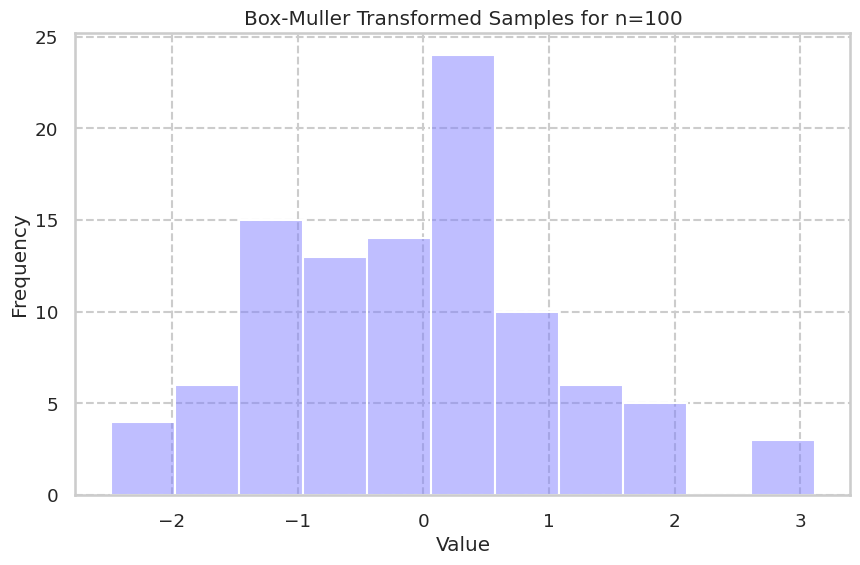
 二項分布の正規近似との比較二項分布のnを大にすると正規近似できる．n=10^2程度でもそこそこ近似できていた．
https://zenn.dev/shundeveloper/articles/986899a7a29e2d
n=10000で比べるとあまり違いはわからない．

 計算速度Colabで回していた時に気づいたが，Box-Muller変換によるサンプリングは重い．

Marsaglia polar methodやZiggurat algorithmなどと比べると，三角関数と対数関数を使っている影響かもしれない．(ベンチマークは他の方に譲ります)
https://en.wikipedia.org/wiki/Marsaglia_polar_method
https://en.wikipedia.org/wiki/Ziggurat_algorithm

 参考文献久保川.2017."現代数理統計学の基礎".共立出版