この記事は英語版wikipedia「De Moivre–Laplace theorem」の解説を行う. すなわち, 二項分布の正規近似について取り扱う. 一方で二項分布の期待値・分散などの基本的性質については記事では触れない.
二項分布の基本的な性質および証明については「二項分布の期待値と分散, 最尤推定, 可視化」という記事で扱ったので適宜参照されたい.
ド・モアブル-ラプラスの定理
定理
二項分布に従う確率変数 X を定義する. このとき n \to \inftyにおいて, 近似的に以下が成り立つ.
\begin{align*}
\frac{X-np}{\sqrt{npq}} \sim N(0,1)
\end{align*}
より厳密には以下である
n\to\infty \text{において} X \sim Bin(n,k),
\frac{X-np}{\sqrt{npq}} \quad \: \text{は 標準正規分布に従う}\\
\text{すなわち, }X\text{ の確率質量と標準正規分布の確率密度の比が1に近づく}\\
\text{これは任意の有限な正の点}k\text{において示すことができる}\\
\text{スケールされていない}X\text{においては以下のように定義される.}
証明
そもそも, \muと\sigmaをパラメータとして持つ正規分布は以下の微分方程式によって定義されている.
\begin{align*}
f'(x)=-\frac{x-\mu}{\sigma^2}f(x)\\
\text{with an initial condition}&\quad
\int_{-\infty}^{\infty}f(x)dx = 1
\end{align*}
二項分布がこの微分方程式を満たしていれば, その極限は正規分布に近づく.
二項分布は離散なので, 極限が微分方程式に変形する差分方程式として始める.
微分方程式は離散微分p(k+1)-p(k), を1ステップサイズの差分として用いる. n \to \infty, において, 離散微分は連続微分となる. 従って, 証明はスケールされていない二項分布に対して以下のみを示せばよい.
\frac{f'(x)}{f(x)}\cdot \biggl(
-\frac{\sigma^2}{x-\mu}
\biggr)
\to 1\; as\; n\to\infty
求められている結果は直接示される.
\begin{align*}
\frac{f'(x)}{f(x)}
\frac{npq}{np-k}
&=
\frac{1}{p(n,k)}
\frac{p(n,k+1)-p(n,k)}{k+1-k}
\frac{\sqrt{npq}}{-c}\\
&=
\frac{p(n,k+1)-p(n,k)}{p(n,k)}
\frac{\sqrt{npq}}{-c}\\
&=
\biggl(
\frac{p(n,k+1)}{p(n,k)}-1
\biggr)
\frac{\sqrt{npq}}{-c}
\\
&=
\biggl(
\frac{
\frac{n!}{(k+1)!(n-k-1)!}p^{k+1}q^{n-k-1}
}
{
\frac{n!}{k!(n-k)!}p^{k}q^{n-k}
}
-1
\biggr)
\frac{\sqrt{npq}}{-c}
\\
&=
\biggl(
\frac{(n-k)p}{(k+1)q}
-1
\biggr)
\frac{\sqrt{npq}}{-c}
\\
&=
\biggl(
\frac{(n-k)p-(k+1)q}{(k+1)q}
\biggr)
\frac{\sqrt{npq}}{-c}
\\
&=
\biggl(
\frac{np-kp-kq-q}{(k+1)q}
\biggr)
\frac{\sqrt{npq}}{-c}
\\
&=
\biggl(
\frac{np-k(p+q)-q}{(k+1)q}
\biggr)
\frac{\sqrt{npq}}{-c}
\\
&=
\biggl(
\frac{np-k-q}{kq+q}
\biggr)
\frac{\sqrt{npq}}{-c}
\\
&=
\biggl(
\frac{-(k-np)-q}{kq+q}
\biggr)
\frac{\sqrt{npq}}{-c}
\\
&=
\biggl(
\frac{-c\sqrt{npq}-q}{npq+cq\sqrt{npq}+q}
\biggr)
\frac{\sqrt{npq}}{-c}
\\
&\to 1
\end{align*}
最後が成り立つのは、n\to 0となるにつれて、-cnpq という項が分母と分子の両方を支配するためである
kはちょうど積分値をとるので、定数cには丸め誤差が発生する。しかし、この誤差の最大値である0.5npqは消滅する値である
変形に関しては以下を参考にされたい.
- cについての変形
\begin{align*}
\frac{k-np}{\sqrt{npq}}&=c\\
-\frac{k-np}{\sqrt{npq}}&=-c\\
-\frac{\sqrt{npq}}{k-np}&=-\frac{1}{c}\\
-\frac{npq}{k-np}&=-\frac{\sqrt{npq}}{c}
\end{align*}
\begin{align*}
\frac{k-np}{\sqrt{npq}}&=c\\
-\frac{k-np}{\sqrt{npq}}&=-c\\
-(k-np)&=-c\sqrt{npq}\\
\end{align*}
- kについての変形
\begin{align*}
k &=
np+c\sqrt{npq}
\\
kq &=
npq+c\sqrt{npq}\;q
\end{align*}
可視化
定理を証明したので, 可視化を行い確認する. pを固定して, n を変化させてシュミレーションを行った. 下記はp=0.5の二項分布からサンプリングしそれぞれの成功回数の確率を可視化したものである.
※ 期待値も分散もnについてみれば一次関数なのでnが増えれば期待値も分散も大きくなる. これについては「二項分布の期待値と分散, 最尤推定, 可視化」という記事で扱ったので適宜参照されたい.
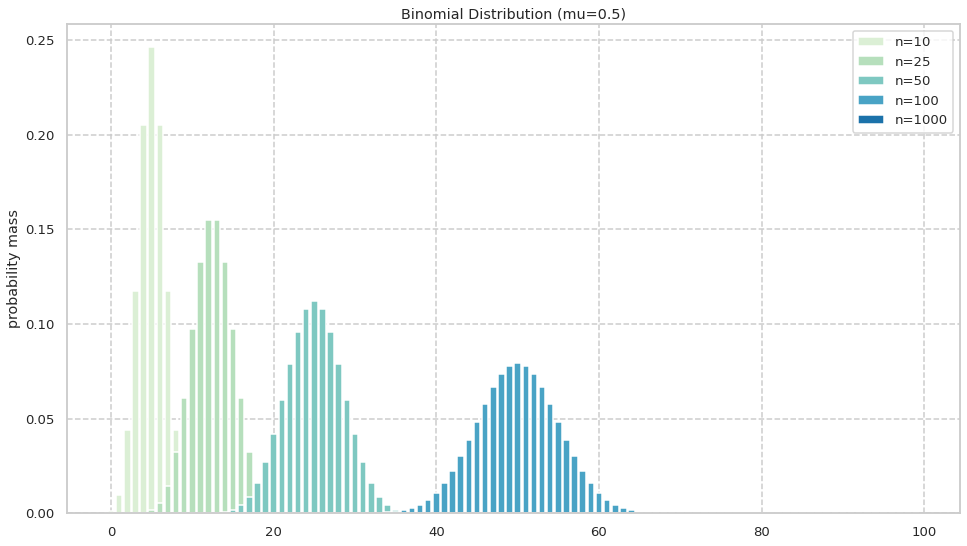
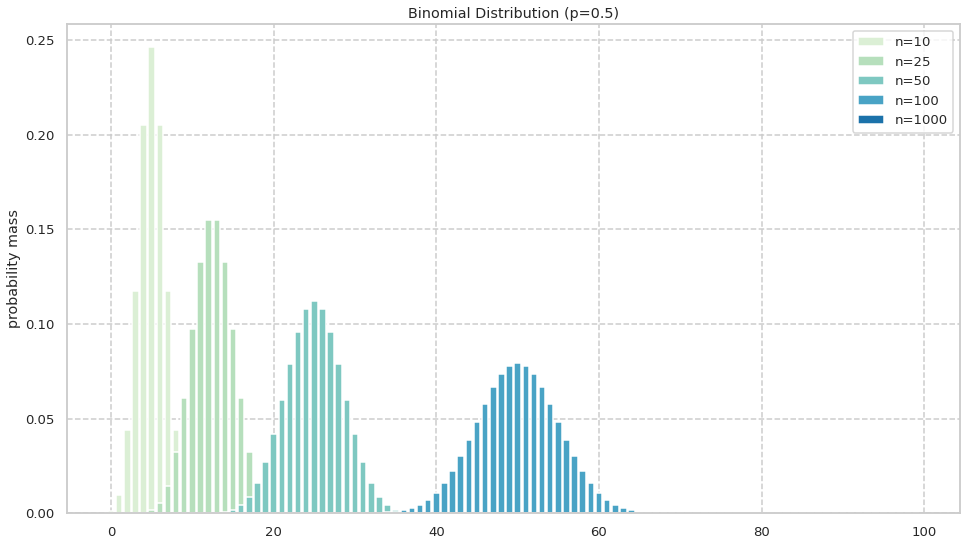
n=1000を追加した図が以下である. n が十分大きくなると収束し, 分布の形に変化が見られなくなることがわかる.
参考文献
Wikipedia."De Moivre–Laplace theorem".2022/5/5 (last edit)
Zenn."二項分布の期待値と分散, 最尤推定, 可視化".2022/11/19 (last edit)


Discussion