Zenn
📊

[統計学] ベルヌーイ分布の期待値と分散, 積率母関数, ベイズ推定

2022/11/12に公開
Python
機械学習
#
統計
tech

確率質量関数

確率質量関数は下記のように定義される.

\begin{align*} Bern(x|\mu) &= \mu^x (1-x)^{(1-x)}\\ x&=\{0,1\},\; \mu=[0,1] \end{align*}

ただし, \mu は平均である.

期待値・分散

確率変数のとる値が0と1の二つで和の計算が簡単である.

期待値

\begin{align*} \mathbb{E}(X) &= \sum_{x=0}^1 x\mu^x(1-\mu)^{(1-x)}\\ &= 0\cdot\mu^0 (1-\mu)^1 + 1 \cdot\mu^1(1-\mu^0)\\ &= \mu \end{align*}

分散

\begin{align*} \mathbb{E}(X^2) &= \sum_{x=0}^1 x^2\mu^x(1-\mu)^{(1-x)}\\ &= 0^2\mu^0(1-\mu)^1 + 1^2\mu^1(1-\mu)^0\\ &= \mu \end{align*}

よって

\begin{align*} \mathbb{V}(X) &= \mathbb{E}(X^2) - \mathbb{E}(X)^2\\ &= \mu-\mu^2\\ &= \mu(1-\mu) \end{align*}

積率母関数

積率母関数(モーメント母関数)を用いると期待値・分散の導出が完結にできることがある. ベルヌーイ分布の場合, 前述の理由によりあまり恩恵を得られないが, 正規分布などでは置換積分や部分積分などといった複雑な計算を避けることが出来る.

積率母関数の定義に基づいてベルヌーイ分布の積率母関数を導出する.

\begin{align*} M_X(t) &= \mathbb{E}(e^{tX}) \\ &= \sum_{x=0}^1 e^{tx} \mu^x (1-\mu)^{(1-x)} \\ &= e^{t\cdot 0} \mu^0 (1-\mu)+ e^t\mu(-1\mu)^0 \\ &= (1-\mu)+e^t \mu \end{align*}

積率母関数を用いて期待値・分散を求める. モーメント母関数にはk回tで微分した式が t=0 の近傍でk次のモーメントになるという性質があるので以下のように導出できる.

期待値

\begin{align*} \mathbb{E}(X) &= M_X(t)' \; |_t=0 \\ &= (1-\mu)' + (\mu e^t)' \; |_{t=0} \\ &= 0+\mu e^t \; |_{t=0} \\ &= \mu \end{align*}

分散

\begin{align*} \mathbb{E}(X^2) &= M_X(t)'' \; |_{t=0} \\ &= (\mu e^t)' \; |_{t=0} \\ &= \mu \end{align*}

ただし, 二行目は期待値の時に導出した一回微分を用いている. 以上より,

\begin{align*} \mathbb{V}(X) &= \mathbb{E}(X^2) - \mathbb{E}(X)^2\\ &= \mu-\mu^2\\ &= \mu(1-\mu) \end{align*}

可視化

期待値と分散の関係性

期待値分散が導出できたので, それぞれの関係性を見ていく. 分散が期待値の二次関数になっており, 二次の項が負であることから上に凸の関数になることがわかる. 実際に図にすると以下のようになる.

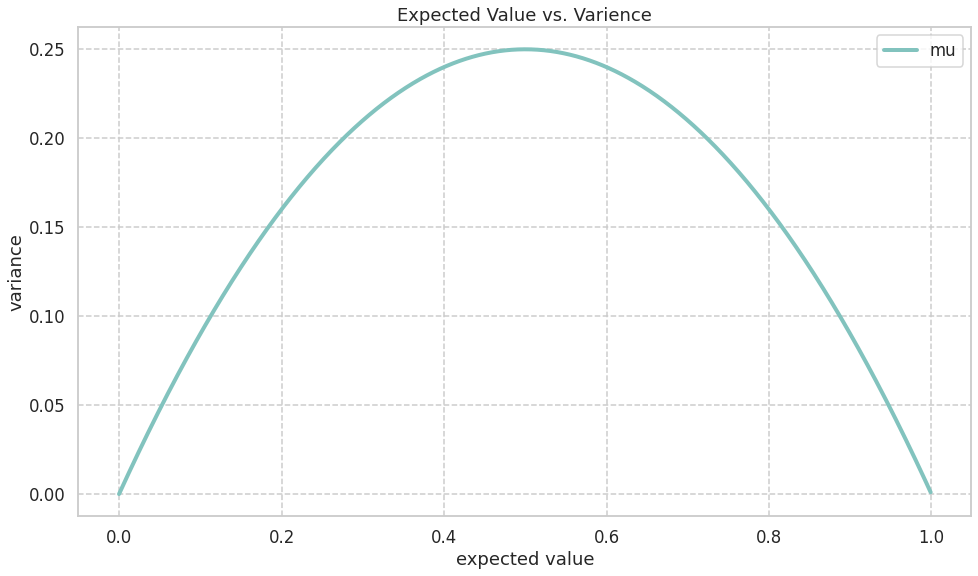
https://storage.googleapis.com/zenn-user-upload/3c183ff28c77-20221107.png

描画に使用したコードを掲載する. これらはGoogle Colabで2022/11/12現在使用可能である.
必要なライブラリをimport

import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
import seaborn as sns

グラフの描画

sns.set()
sns.set_style("whitegrid", {'grid.linestyle': '--'})
sns.set_context("talk", 1, {"lines.linewidth": 4})
sns.set_palette("GnBu", 1, 0.8)

fig=plt.figure(figsize=(16,9))
ax = fig.add_subplot(1, 1, 1)
ax.set_title('Expected Value vs. Varience')
ax.set_xlabel('expected value')
ax.set_ylabel('variance')

x = np.arange(0, 1, 0.001)
ax.plot(x, x*(1-x))

ax.legend(['mu'])

plt.show()

期待値が変化したときの分布形の変化

\muに対して分布の形は以下のように変化する.

https://storage.googleapis.com/zenn-user-upload/a1bc27dc9b88-20221107.png

同じく描画に使用したコードを掲載する. ただし, ライブラリのimportは先ほどと同じなので省略する

sns.set()
sns.set_style("whitegrid", {'grid.linestyle': '--'})
sns.set_context("talk", 0.8, {"lines.linewidth": 0})
sns.set_palette("GnBu", 6, 0.8)

x = ['x=0','x=1']

fig=plt.figure(figsize=(16,9))
ax1 = fig.add_subplot(1, 3, 1)
ax1.set_title('Bernoulli Distribution (mu=0.2)')
ax1.set_ylabel('probability mass')
ax1.bar(x, [0.25,0.75])

ax2 = fig.add_subplot(1, 3, 2)
ax2.set_title('Bernoulli Distribution (mu=0.5)')
ax2.set_ylabel('probability mass')
ax2.bar(x, [0.5,0.5])

ax3 = fig.add_subplot(1, 3, 3)
ax3.set_title('Bernoulli Distribution (mu=0.75)')
ax3.set_ylabel('probability mass')
ax3.bar(x, [0.75,0.25])

plt.show()

最尤推定

対数尤度関数の導出

ベルヌーイ分布に独立同一に従う確率変数の観測値 x_i を要素に持つデータを以下のように定義する.

\begin{align*} \mathbf{x}=\{x_1 \: x_2 \cdots \: x_n\} \end{align*}

このとき対数尤度関数は,

\begin{align*} \ln L(\mu) &= \ln p(\mathbf{x}|\mu) \\ &= \ln \prod_{i=1}^N p(x_i|\mu) \\ &= \sum_{i=1}^N \ln p(x_i|\mu) \\ &= \sum_{i=1}^N \ln \biggl( \mu^{x_i}(1-\mu)^{(1-x_i)} \biggr) \\ &= \sum_{i=1}^N \biggl( \ln \mu^{x_i} + \ln (1-\mu)^{(1-x_i)} \biggr) \\ &= \sum_{i=1}^N x_i \ln \mu + \sum_{i=1}^N (1-x_i) \ln (1-\mu) \\ &= \sum_{i=1}^N x_i \ln \mu + (N-\sum_{i=1}^N x_i) \ln (1-\mu) \end{align*}

最尤推定量の導出

導出した対数尤度関数をパラメータで微分すると尤度方程式が得られる. 尚, 尤度方程式とは対数尤度関数の極値条件を与える方程式のことである. この尤度方程式の解が最尤推定量となる.

対数尤度関数を微分すると以下の式が得られる.

\begin{align*} \frac{\partial \ln L(\mu)}{\partial \mu} &= \mu^{-1}\sum_{i=1}^N x_i - (1-\mu)^{-1}(N-\sum_i^N x_i)\end{align*}

対数尤度関数の極値はこの式が 0 のときであるから, 以下を満たす\mu_{ML}を導出する.

\begin{align*} \mu^{-1}\sum_{i=1}^N x_i - (1-\mu)^{-1}(N-\sum_{i=1}^Nx_i) &=0 \end{align*}

これを満たす \mu=\mu_{ML} は,

\begin{align*} \mu_{ML}^{-1}\sum_{i=1}^N x_i &= (1-\mu_{ML})^{-1}(N-\sum_{i=1}^N x_i) \\ \frac{1-\mu_{ML}}{\mu_{ML}} &= \frac{N-\sum_{i=1}^N x_i}{\sum_{i=1}^N x_i} \\ \frac{1}{\mu_{ML}}-1 &= \frac{N}{\sum_{i=1}^N x_i}-1 \\ \mu_{ML} &= \frac{1}{N}\sum_{i=1}^N x_i \end{align*}

ベイズ推定

事後分布の導出

観測値 x_i を要素に持つデータを観測したとし, 以下のように記述する.

\begin{align*} \mathbf{x}=\{x_1 \: x_2 \cdots \: x_n\} \end{align*}

このとき事後分布は,

\begin{align*} p(\mu|\mathbf{x}) &= \frac{p(\mathbf{x}|\mu)p(\mu)}{p(\mathbf{x})}\\ &= \frac{\prod_{i=1}^N p(x_i|\mu)p(\mu)}{p(\mathbf{x})}\\ &\propto \prod_{i=1}^N p(x_i|\mu)p(\mu) \end{align*}

なお, p(\mu) はベルヌーイ分布の事前分布であるベータ分布を用いる. ベータ分布の定義は以下である.

Beta(a,b) = \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}\mu^{(a-1)}(1-\mu)^{(b-1)}

事後分布の対数をとると,

\begin{align*} \ln p(\mu|\mathbf{x}) &\propto \sum_{i=1}^N \ln p(x_i|\mu)+\ln p(\mu)\\ &= \sum_{i=1}^N \biggl( \ln \bigl[ \mu^{x_i}(1-\mu)^{1-x_i} \bigr] \biggr) + \ln \bigl[ \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)} \mu^{(a-1)}(1-\mu)^{(b-1)} \bigr]\\ &= \sum_{i=1}^N \biggl( \ln \mu^{x_i} + \ln (1-\mu)^{(1-x_i)} \biggr) + \ln \mu^{a-1}+\ln(1-\mu)^{b-1}+\text{const.} \\ &= \sum_{i=1}^N \biggl( x_i \ln \mu + (1-x_i) \ln (1-\mu) \biggr) + (a-1) \ln \mu+(b-1)\ln(1-\mu)+\text{const.} \\ &= \sum_{i=1}^Nx_i \ln \mu + (N-\sum_{i=1}^Nx_i) \ln (1-\mu) + (a-1) \ln \mu+(b-1)\ln(1-\mu)+\text{const.} \\ &= (\sum_{i=1}^Nx_i+a-1) \ln \mu + (N-\sum_{i=1}^Nx_i+b-1) \ln (1-\mu) + \text{const.} \end{align*}

ただし, 5行目第二項の係数は \sum_i^N(1-x_i) を変形した結果であることに注意されたい. ベータ分布に対数をとると,

\begin{align*} \ln Beta(a,b) &= \ln \biggl[ \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)} \mu^{(a-1)}(1-\mu)^{(b-1)} \biggl] \\ &= \ln \mu^{(a-1)} + \ln (1-\mu)^{(b-1)} + \text{const.} \\ &= (a-1) \ln \mu + (b-1) \ln (1-\mu) + \text{const.}\end{align*}

前述の式と照らし合わせることで, 事後分布が以下であることが分かる.

\begin{align*} p(x|\mu) &= Beta(a^\star, b^\star)\\ a^\star&=\sum_i^Nx_i+a\\ b^\star&=N-\sum_i^Nx_i+b \end{align*}

事後分布のパラメータを事前分布のパラメータと比べると成功の数と失敗の数がそれぞれのパラメータに足されていることが分かる.

予測分布の導出

事後分布が求まったので予測分布を導出する. 予測分布は\mu に対して尤度関数で期待値をとることで導出できる. 便宜上先ほど求めた a^\star, \: b^\star は最後に代入することとする.

\begin{align*} p(x_\star) &= \int p(x_\star|\mu)p(\mu|a, b)\:d\mu \\ &= \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)} \int \mu^{x_\star}(1-\mu)^{(1-x_\star)} \mu^{(a-1)}(1-\mu)^{(b-1)} \:d\mu \\ &= \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)} \int \mu^{x_\star+a-1}(1-\mu)^{(1-x_\star+b-1)}\:d\mu\\ &= \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)} \frac{\Gamma(x_\star+a)\Gamma(1-x_\star+b)}{\Gamma(a+b+1)} \end{align*}

最終行は確率密度関数の積分が1であることと, ベータ分布の正規化項を用いている. 以下参考.

\begin{align*} \int Beta(\mu|a,b)\:d\mu&=1\\ \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)} \int \mu^{(a-1)}(1-\mu)^{(b-1)} \:d\mu&=1\\ \therefore \int \mu^{(a-1)}(1-\mu)^{(b-1)} \:d\mu &= \frac{\Gamma(a)\Gamma(b)}{\Gamma(a+b)} \end{align*}

予測分布が求まったのでx_\star = 0,1のそれぞれの確率を求める.

\begin{align*} p(x_\star=0) &= \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)} \frac{\Gamma(x_\star+a)\Gamma(1-x_\star+b)}{\Gamma(a+b+1)}\\ &= \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)} \frac{\Gamma(a)\Gamma(1+b)}{\Gamma(a+b+1)}\\ &= \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)} \frac{\Gamma(a)\:b\:\Gamma(b)}{(a+b)\:\Gamma(a+b)}\\ &= \frac{b}{(a+b)} \end{align*}
\begin{align*} p(x_\star=1) &= \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)} \frac{\Gamma(x_\star+a)\Gamma(1-x_\star+b)}{\Gamma(a+b+1)}\\ &= \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)} \frac{\Gamma(a+1)\Gamma(b)}{\Gamma(a+b+1)}\\ &= \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)} \frac{a\:\Gamma(a)\Gamma(b)}{(a+b)\:\Gamma(a+b)}\\ &= \frac{a}{(a+b)} \end{align*}

それぞれの確率が求まったので, 予測分布が以下の形であることがわかる.

Bern \biggl( \frac{a}{(a+b)},\frac{b}{(a+b)} \biggr)

a,\: b にそれぞれ, a^\star, \: b^\star を代入すると, 学習後の予測分布が求まる.

Bern \biggl( \frac{\sum_i^Nx_i+a}{(a+b+N)},\frac{N-\sum_i^Nx_i+b}{(a+b+N)} \biggr)

参考文献

(1) 竹村彰通.”新装改訂版 現代数理統計学”.2020.学術図書出版社
(2) 一般社団法人 日本統計学会.”日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブック”.2020.学術図書出版社
(3) 一般社団法人 日本統計学会.”日本統計学会公式認定 統計検定1級対応 統計学”.2013.東京図書出版社
(4)C.M.ビショップ.”パターン認識と機械学習 上 ベイズ理論による統計的予測”.2019.丸善出版株式会社
(5)須山敦志.”機械学習スタートアップシリーズ ベイズ推論による機械学習入門”.2018.株式会社講談社サイエンティフィク

参考サイト

(1) matplotlib document
(2) scipy document

Discussion