テイラー展開とは

「テイラー展開」を前提知識なしでいきなり理解してみる。難しいことじゃない。

テイラー展開の概念

テイラー展開ってなに

テイラー展開とは、そのままでは扱いにくい 関数 を 級数 の形に近似すること。

たとえば、$\pi$ の値はいくらですかときかれたら（ $\pi$ が関数かはともかく、イメージとして）、

$$\pi=3+0.1+0.04+0.001+0.0005+ \cdots$$

のように級数の形にしてしまう。

そして
「１次近似で」といわれたら

$$\pi\fallingdotseq 3 \quad (\pi\text{は約}3\text{です！})$$

「２次近似で」といわれたら

$$\pi\fallingdotseq 3+0.1 \quad (\pi\text{は約}3.1\text{です！})$$

「３次近似で」といわれたら

$$\pi\fallingdotseq 3+0.1+0.04 \quad (\pi\text{は約}3.14\text{です！})$$

という具合に、ひとつずつ後ろの項を含めていくことで、正確な近似になっていく。なので理論上は「 $\infty$ 次近似」をすれば元の関数と同じ値になる(※)。が、そもそも近似で構わないわけだから、実際はいいところで切って近似値を得る。

※後述するが、収束半径が $\infty$ である必要がある。

テイラー展開を使う場面

どういうときにテイラー展開をするかといえば、 ある関数がそのままでは扱いにくい時 。たとえば積分したいがそのままではかなり大変なときなど。

もちろんテイラー展開をすればそれは「近似値」になるが、誤差が許容範囲に収まるように〜次近似を設定すればよい。

もうすこし踏み込んで視覚的にみてみる

グラフで視覚的に見てもらったほうが早い。
たとえば、こういう関数がある。

これをテイラー展開で近似する。
近似なわけだから、どこの位置から近似を始めるかを決めなきゃいけない。
今回は $x=1$ から近似していくことにする。

まず、１次近似はこうなる。

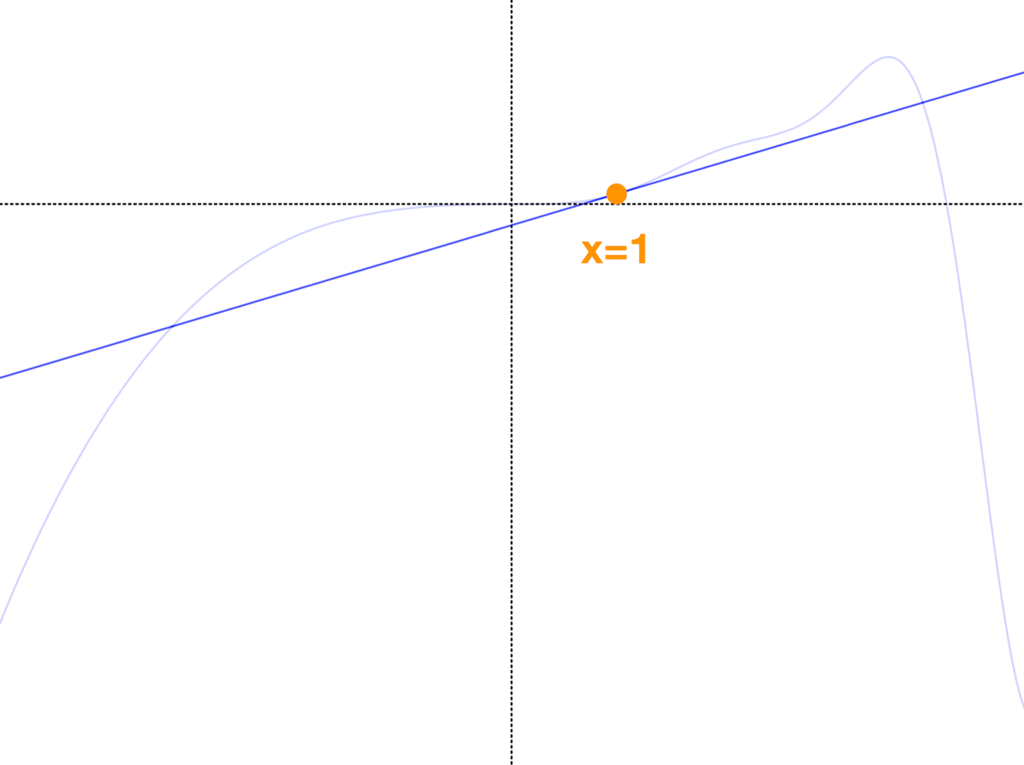
x=1での１次近似

１次近似は x=1の点での傾きそのもの となった。

２次近似、３次近似を見てみよう。

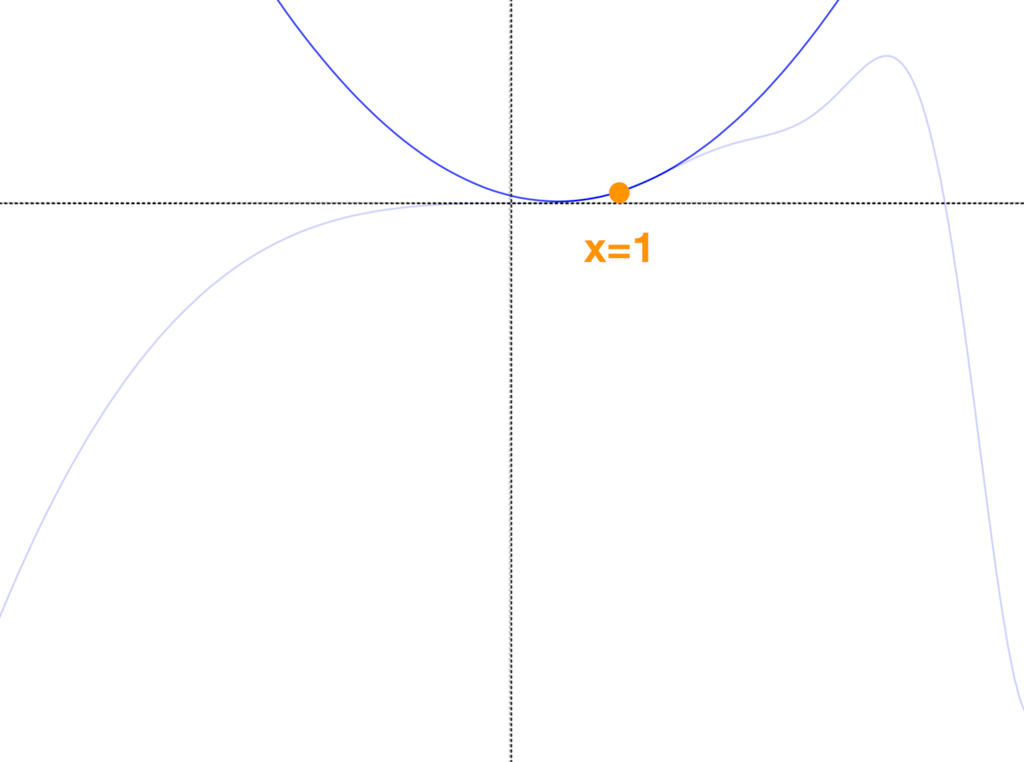
x=1での２次近似

x=1での３次近似

こんな具合に $x=1$ を中心にちょっとずつ元の形に近づいている。

9次近似、15次近似になるとこうなる。

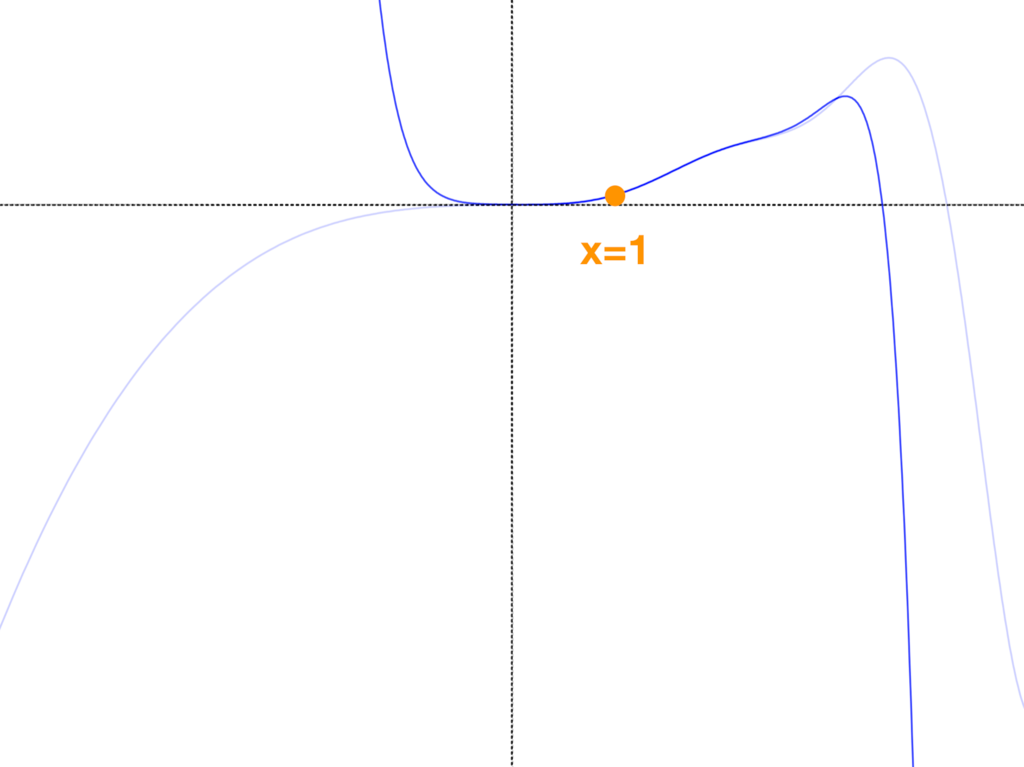
x=1での9次近似

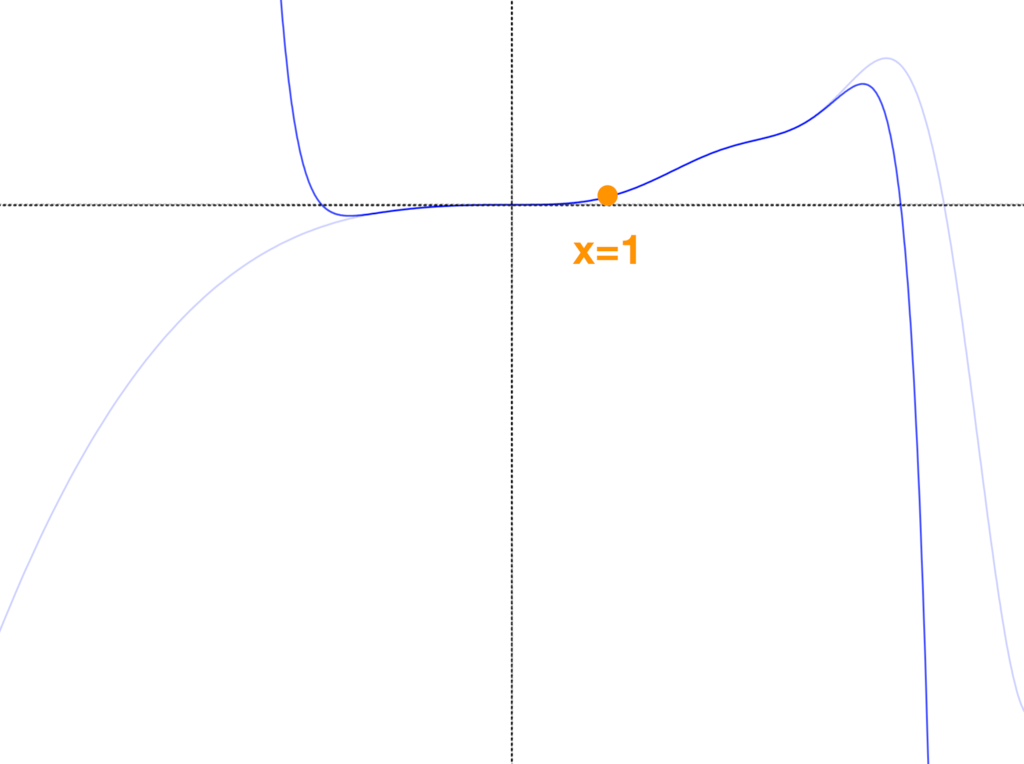
x=1での15次近似

なんとなくイメージがつかめたろう。大事なのは、テイラー展開は ある場所を中心に近似する ということ。今回は $x=1$ を中心に近似している。これを 「x=1のまわりでテイラー展開する」 という。

ちなみに $x=0$ のまわりでテイラー展開することを マクローリン展開 というらしい。やることはテイラー展開と同じ。

近似できる範囲

テイラー展開は、近似を始める場所からあまりにも離れたところまでは近似できないことがある。この近似できる範囲を 収束半径 という。

収束半径が $\infty$ ならどこまででも近似できるし、 $0$ ならそもそもテイラー展開できないということになる。

収束半径の求め方

収束半径を求めるには２通りの方法がある。

$f(x)$ を $x=a$ のまわりでテイラー展開するとき、

$\displaystyle C_n=\frac{f^{(n)} (a)}{n!}$ とすると ( $f^{(n)}(a)$ は $f(a)$ の $n$ 階微分)

$$\begin{align*} {\small \text{ダランベールの方法 :}} \quad & \text{収束半径} ~ r &= \lim_{n \to \infty} \big|\frac{C_n}{C_{n+1}}\big| \\[2em] {\small \text{コーシー・アダマールの方法 :}} \quad & \text{収束半径} ~ r &= \lim_{n \to \infty} \frac{1}{\sqrt[n]{|C_n|}} \end{align*}$$

どちらの方法でもいい。ダランベールの方法の方が直感的だしやりやすいと思う。要するに、先の項より後の項の係数が小さくなっていればいいわけだ。

なぜこれで求まるのか

詳細な説明はしないが、要するに項の数を増やすごとに項の値が小さくなっていって、無限に項を増やしていって最後の項の値が $0$ となればテイラー展開成功なわけだ。厳密にいうと最後の項というよりは「誤差項」というのを用意して、それが $0$ に収束すればいいのだが、イメージとしては同じことだ。

なので 誤差項が0に収束するxの範囲 を求めればよい。その方法が上の２つの方法だ。

詳細な導出はこちらのページでやられている。
http://cis.k.hosei.ac.jp/~kano/math_2005/calculus/RatioTest.pdf
http://eman-physics.net/math/series.html

テイラー展開の具体的な方法

関数 $f(x)$ を

• $x=a$ のまわりで
• $n$ 次近似で

テイラー展開すると、以下のように近似できる。

$\displaystyle C_n=\frac{f^{(n)} (a)}{n!}$ として ( $f^{(n)}(a)$ は $f(a)$ の $n$ 階微分)

$$\begin{align*} f(x) & \fallingdotseq \sum_{k=0}^{n} \left[ C_k(x-a)^k \right] \\[2em] & \fallingdotseq C_0 (x-a)^0 + C_1 (x-a)^1 + C_2 (x-a)^2 \cdots \end{align*}$$

• ただし $\quad a-r < x < a+r \quad$ ( $r$ は収束半径)
• $\infty$ 次近似すれば元の関数と同じ値になる。

説明

概念的な話になるが。
ポイントは $(x-a)^k$ の部分。 $x=a$ のまわりでテイラー展開しているわけだから xはだいたいaの近く だ。最初のグラフでみたように $a$ (例のグラフの場合は $1$ )の近くから近似していく。なので $(x-a)$ はとても小さい値になる。

とても小さな値を $(x-a)^2$ とか $(x-a)^3$ とかしたらもっと小さくなる。なので 項の数が増えるに従って、増加する数は小さくなっていく 。でないと（項を増やすごとに増加する量が増えていったら）、項の数を $\infty$ にしたら値も $\infty$ に発散してしまう。テイラー展開が元の関数の形に収束する条件は、項の数が増えるに従って増加する数が小さくなっていくこと、つまり 先の項よりも後の項の方が小さいこと なのだ。

例題

$f(x)=2^x$ を $x=1$ のまわりで $3$ 次近似でテイラー展開せよ。

1. 収束半径を求める

ダランベールの方法で収束半径を求める。

$$C_n=\frac{f^{(n)} (1)}{n!} \quad , \quad C_{n+1}=\frac{f^{(n+1)} (1)}{(n+1)!}$$

なので、 $f^{(n)}(x)$ がどうなるのか一般化したい。(指数関数の微分)

$$\begin{align*} & (2^x)' &=&~ 2^x \ln 2 \\[1em] & (2^x)'' &=&~ (2^x \ln 2)' ~=~ 2^x (\ln 2)^2 \\[1em] & (2^x)''' &=&~ (2^x (\ln 2)^2)' ~=~ 2^x (\ln 2)^3 \\[1em] & \cdots \end{align*}$$

なので $f^{(n)}(x)=2^x (\ln 2)^n$ と書ける。

これをふまえると、

$$\begin{align*} C_n &= \frac{f^{(n)} (1)}{n!}=\frac{2^1 (\ln 2)^n}{n!} \\[2em] C_{n+1} &= \frac{f^{(n+1)} (1)}{(n+1)!}=\frac{2^1 (\ln 2)^{n+1}}{(n+1)!} \end{align*}$$

ダランベールの方法によると

$$\text{収束半径} ~ r = \lim_{n \to \infty} \big|\frac{C_n}{C_{n+1}}\big| = \lim_{n \to \infty} \Bigg| \frac{\frac{2^1 (\ln 2)^n}{n!}}{\frac{2^1 (\ln 2)^{n+1}}{(n+1)!}} \Bigg|$$

$(n+1)!=(n+1)n!$ だから

$$\begin{align*} r &= \lim_{n \to \infty} \Bigg| \frac{\frac{2^1 (\ln 2)^n}{n!}}{\frac{2^1 (\ln 2)^{n+1}}{(n+1)!}} \Bigg| \\[2em] &= \lim_{n \to \infty} \Bigg|\frac{2(\ln 2)^n (n+1)}{2(\ln 2)^{n+1}}\ \Bigg| \\[2em] &= \lim_{n \to \infty} \big| \frac{n+1}{\ln 2}\ \big| \\[2em] &= \infty \end{align*}$$

よって $f(x)=2^x$ の収束半径は $\infty$ 。

ということで、 $f(x)=2^x$ はすべての範囲でテイラー展開できることがわかった。

2. テイラー展開する

$f(x)=2^x$ を $x=1$ のまわりで $3$ 次近似でテイラー展開する。

今回は３次近似なので

$$f(x)\fallingdotseq C_0 (x-a)^0 +C_1 (x-a)^1 + C_2 (x-a)^2 + C_3 (x-a)^3$$

を求める。

まず $C_n$ は収束半径を求める際に計算した。

$$C_n=\frac{f^{(n)} (1)}{n!}=\frac{2 (\ln 2)^n}{n!}$$

これをあてはめると、

$$\begin{align*} f(x) &\fallingdotseq C_0(x-1)^0 + C_1(x-1)^1 + C_2(x-1)^2 + C_3(x-1)^3 \\[1.5em] &\fallingdotseq \frac{2 (\ln 2)^0}{0!} (x-1)^0 +\frac{2 (\ln 2)^1}{1!}(x-1)^1 + \frac{2 (\ln 2)^2}{2!} (x-1)^2 + \frac{2 (\ln 2)^3}{3!} (x-1)^3 \\[1.5em] &\fallingdotseq \ 2\ +\ 2 (\ln 2)(x-1)\ +\frac{2 (\ln 2)^2}{2} (x-1)^2+\frac{2 (\ln 2)^3}{6} (x-1)^3 \end{align*}$$

と求まった。

グラフで確認

これでどのくらい近似できたのかグラフでみてみよう。

1つめがもとの関数 $f(x)=2^x$ 、2つめがいま求めた3次近似。

元の関数

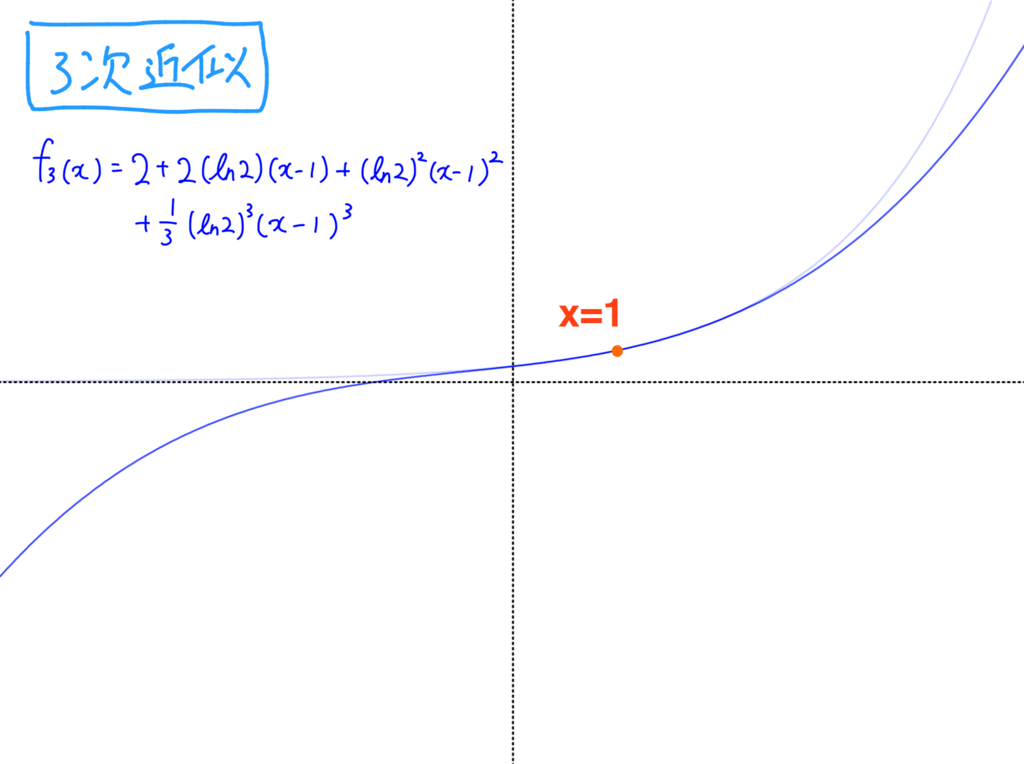
3次近似

まだ大きく離れている箇所もあるが $x=1$ の近くはだいたい重なっている。

ちなみに6次近似、10次近似になるとこうなる。

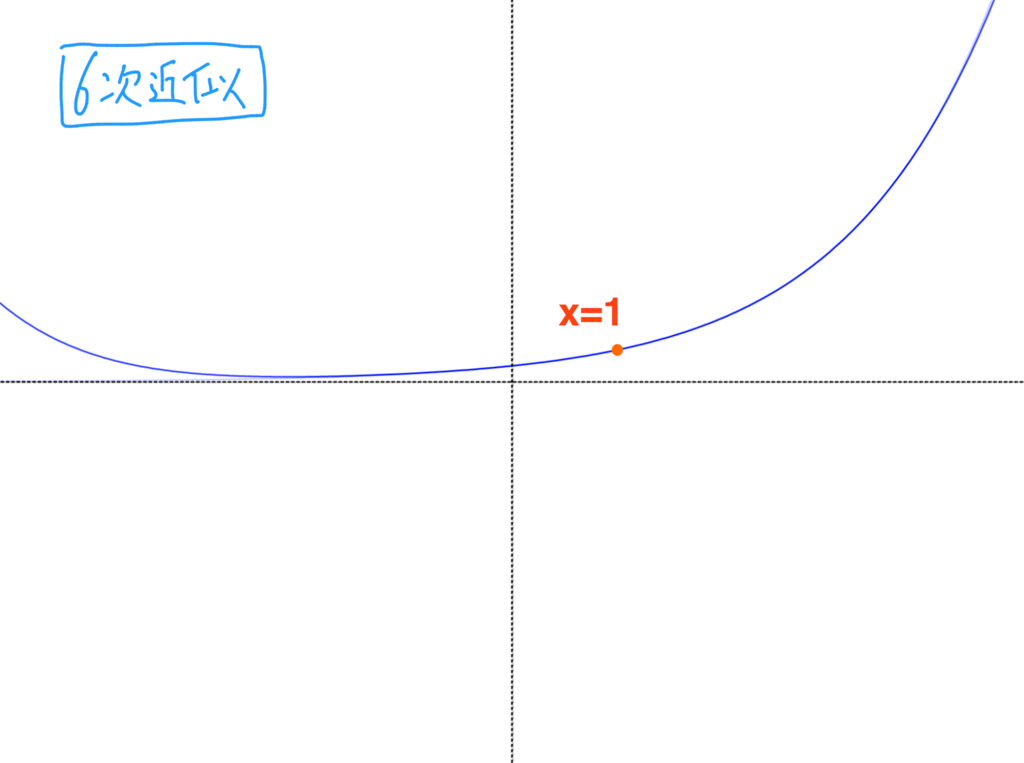
6次近似

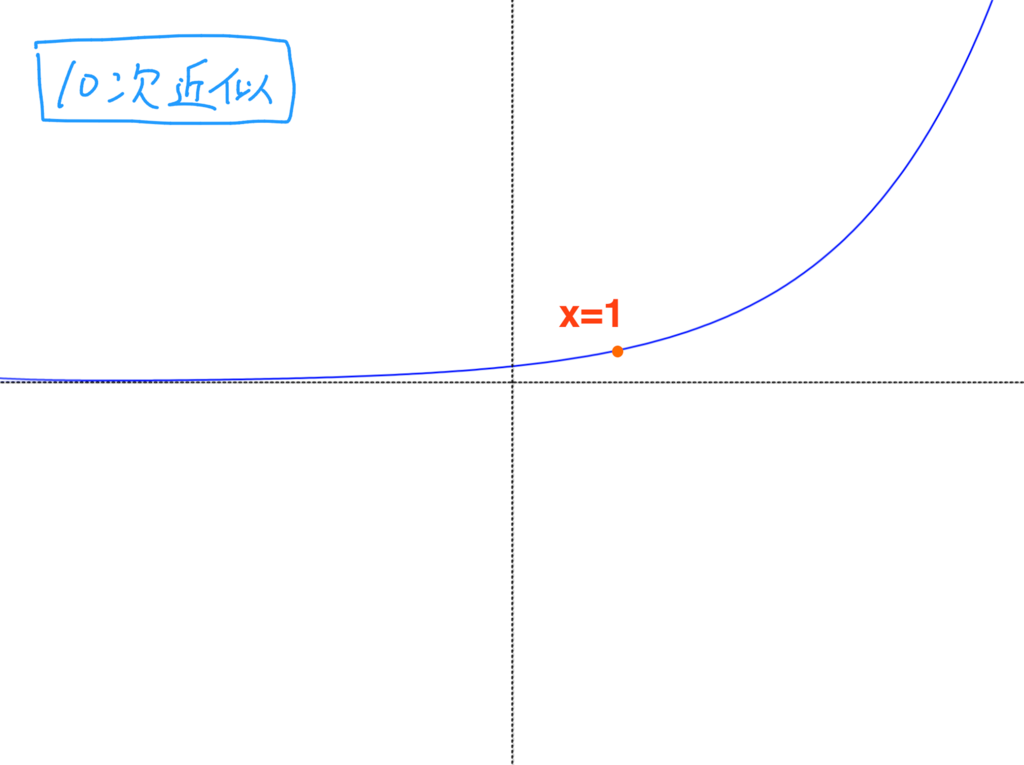
10次近似