『JavaScriptで学ぶ関数型プログラミング』を読んだ 02

https://zenn.dev/shimpei_takeda/articles/ec37a19bbf0e7a
01からのつづき

5. 関数を組み立てる関数

...
つづき

部分適用

• 部分適用
  • カリー化と部分適用
    • カリー化された関数は、引数が渡されるたびにパラメータが無くなるまで徐々に動作を特化された関数を返す
    • 部分適用（partial application）された関数は「部分的に」実行されており、期待している残りの引数を与えることで即時実行する用意をしている関数となる
    • カリー化と部分適用には、「1つ以上の数の引数を専門化することによって合成する」と言う共通の制約がある
      • 引数と戻り値の関係性にもとづいて関数を合成したい場合は、次節の関数を並べてつなぎ合わせるcompose関数がある
    • 部分適用の例
      • 部分適用とカリー化の違い
        • 見た目は同じように見える
        • 部分適用では一回の適用に際して扱う引数の数は必ずしも一つだけではなく、複数の引数を扱うこともできるという点にある
        • また、カリー化は関数がパラメータリストの右から左に向かって動作する
        • 部分適用は、可変長の引数を取る関数でも混乱しにくい
      • 部分適用の例

          function divPart(n) {
            return function(d) {
              return n/d;
            };
          }
          
          var over10Part = divPart(10);
          over10Part(2);
          //=> 5
        

  • 1つ・2つの既知の引数を部分適用する
    • partial関数の例

        /*
          partial1関数から返される関数は、
          partial1の実行時にその引数arg1を確保し、
          引数リストの先頭に追加する
        */
        function partial1(fun, arg1) {
          return function(/* args */) {
            var args = construct(arg1, arguments);
            return fun.apply(fun, args);
          };
        }
        
        var over10Part1 = partial1(div, 10);
        
        over10Part1(5);
        //=> 2
        
        /*
          関数ともう一つの関数と「設定用」引数を
          合成することによりover10関数を再作成した
          2つまでの引数を部分適用する関数も
          同様に作成できる
        */
        function partial2(fun, arg1, arg2) {
          return function(/* args */) {
            var args = cat([arg1, arg2], arguments);
            return fun.apply(fun, args);
          };
        }
        
        var div10By2 = partial2(div, 10, 2);
        
        div10By2();
        //=> 5
      

  • 任意の数の引数を部分適用する
    • JavaScriptにおいて、カリー化は関数が可変長の引数を取ることにより複雑化されてしまう
      • 任意の数の引数の部分適用は関数合成の戦略として合理的と言える
    • partial関数の例

        /*
          partial関数はいくつかの引数を確保し、
          それらの引数を最初の引数とする関数を返す
        */
        function partial(fun /*, 任意の数の引数 */) {
          var pargs = _.rest(arguments);
        
          return function(/* 引数 */) {
            var args = cat(pargs, _.toArray(arguments));
            return fun.apply(fun, args);
          };
        }
        
        var over10Partial = partial(div, 10);
        over10Partial(2);
        //=> 5
        
        /*
          可変長の引数の存在は
          状況を複雑にすることがある
        */
        var div10zBy2By4By5000Partial = partial(div, 10, 2, 4, 5000);
        div10zBy2By4By5000Partial();
        //=> 5
        // div関数は引数のうち10と2だけを受け取り、残りを無視してしまう
        // ただ、これはレアケースではある
      

  • 部分適用の実用例: 事前条件
    • コードをより宣言型に近づけることができる
      • 宣言型: 「どのように行うべきか」より「何をすべきか」を定義する
    • 部分適用の実用例

        /*
          ckecker関数を使わずに
          validator関数を使う
        */
        var zero = validator("0ではいけません", function(n) { return 0 === n });
        var number = validator("引数は数値である必要があります", _.isNumber);
        
        function sqr(n) {
          if (!number(n)) throw new Error(number.message);
          if (zero(n)) throw new Error(zero.message);
          return n * n;
        }
        
        sqr(10);
        //=> 100
        
        sqr(0);
        // Error: 0ではいけません
        
        sqr('');
        // Error: 引数は数値である必要があります
        
        /*
          部分適用を使用することで
          改良できる
        
          保証のタイプ
          - 事前条件（preconditions): 
            - 関数の呼び出し元の保証
          - 事後条件（postconditions）:
            - 事前条件が満たされたと想定した場合の、関数呼び出しの結果に対する保証
        
          ある関数に、それが取り扱うことができるデータを提供した場合（事前条件）、
          その関数の戻り値はある具体的な基準を満たすことを保証する（事後条件）。
        */
        function condition1(/* 1つ以上の検証関数 */) {
          var validators = _.toArray(arguments);
        
          return function(fun, arg) {
            var errors = mapcat(function(isValid) {
              return isValid(arg) ? [] : [isValid.message];
            }, validators);
        
            if (!_.isEmpty(errors)) 
              throw new Error(errors.join(", "));
        
            return fun(arg);
          };
        }
        
        var sqrPre = condition1(
          validator("0ではいけません", complement(zero)),
          validator("引数は数値である必要があります", _.isNumber)
        );
        
        sqrPre(_.identity, 10);
        //=> 10
        
        sqrPre(_.identity, '');
        // Error: 引数は数値である必要があります
        
        sqrPre(_.identity, 0);
        // Error: 0ではいけません
        
        /*
          安全でないバージョンのsqr関数を
          考えてみる
        */
        function uncheckedSqr(n) { return n * n };
        
        uncheckedSqr('');
        //=> 0
        
        /*
          checkedSqr関数は、sqr関数と同じように動くが、
          内部的に引数の妥当性チェックが
          計算から分離されているため、
          より柔軟になっている（変更容易性が高い）
        */
        var checkedSqr = partial1(sqrPre, uncheckedSqr);
        
        checkedSqr(10);
        //=> 100
        
        checkedSqr('');
        // Error: 引数は数値である必要があります
        
        checkedSqr(0);
        // Error: 0ではいけません
        
        /*
          検証をオフにしたり、
          追加の検証項目を追加したりすることができる
        */
        var sillySquare = partial1(
          condition1(validator("偶数を入力してください", isEven)),
          checkedSqr
        );
        
        sillySquare(10);
        //=> 100
        
        sillySquare(11);
        // Error: 偶数を入力してください
        
        sillySquare('');
        // Error: 引数は数値である必要があります
        
        sillySquare(0);
        // Error: 0ではいけません
        
        /*
          checkCommnad関数を
          検証関数を使って再実装してみる
        */
        var validateCommand = condition1(
          validator("マップデータである必要があります", _.isObject),
          validator("設定オブジェクトは正しいキーを持っている必要があります", hasKeys('msg', 'type'))
        );
        
        var createCommand = partial(validateCommand, _.identity);
        
        createCommand({});
        // Error: マップデータである必要があります
        
        createCommand(21);
        // Error: マップデータである必要があります, 設定オブジェクトは正しいキーを持っている必要があります
        
        createCommand({msg: "", type: ""});
        //=> {msg: "", type: ""}
        
        /*
          関数合成を使うことで、
          実行ロジックや検証プロセスをカスタマイズするために、
          追加の合成を行うことができる
        */
        var createLaunchCommand = partial1(
          condition1(
            validator("設定オブジェクトにはcountDownプロパティが必要です", hasKeys('countDown'))
          ),
          createCommand
        );
        
        createLaunchCommand({msg: "", type: ""});
        // Error: 設定オブジェクトにはcountDownプロパティが必要です
        
        createLaunchCommand({msg: "", type: "", countDown: 10});
        //=> {msg: "", type: "", countDown: 10}
      

並べた関数を端から端までcompose関数でつなぎ合わせる

• 並べた関数を端から端までcompose関数でつなぎ合わせる
  • compose関数とは
    • 理想化された関数型プログラミングは、関数でできたパイプラインのようなもの
      • 一方の端からデータを入れると、逆の端から新しいデータが放出される
    • compose関数でつなぎ合わせる例

        /*
          このパイプラインは、
          _.isString関数と!演算子で構成されている
        */
        !_.isString(name)
        
        /*
          関数合成はデータチェーンを活用して、
          データ変換によって新しい関数を組み立てる
        */
        function isntString(str) {
          return !_.isString(str);
        }
        
        isntString(1);
        //=> true
        
        /*
          compose関数によって、
          上記と全く同じ関数を関数合成で
          組み立てることができる
        */
        var isntString = _.compose(function(x) { return !x }, _.isString);
        
        isntString([]);
        //=> true
        
        /*
          _.compose関数では、
          合成された関数は右から左に実行される
        */
                                       !     _.isString ("a");
        _.compose(function(x) { return !x }, _.isString)("a");
        
        /*
          !演算子を関数でカプセル化して
          利用もできる
        */
        function not(x) { return !x };
        
        var isntString = _.compose(not, _.isString);
        
        /*
          mapcat関数も
          _.composeを使って実装できる
        */
        var composedMapcat = _.compose(splat(cat), _.map);
        
        composedMapcat([1,2],[3,4],[5], _.identity);
        //=> [1,2,3,4,5]
      

  • 合成を使った事前条件と事後条件
    • 事前条件は、ある制約（事後条件）に準拠する戻り値を生成するために関数が必要とする条件を定義している
      • condition1とpartial関数を使って、uncheckedSqrの引数をバリデーションしてから実行する関数checkedSqrを組み立てた
    • 事後条件の例

        var sqrPost = condition1(
          validator("結果は数値である必要があります", _.isNumber),
          validator("結果はゼロではない必要があります", complement(zero)),
          validator("結果は正の数である必要があります", greaterThan(0))
        );
        
        sqrPost(_.identity, 10);
        // Error: 結果はゼロではない必要があります, 結果は正の数である必要があります
        
        sqrPost(_.identity, -1);
        // Error: 結果は正の数である必要があります
        
        sqrPost(_.identity, '');
        // Error: 結果は数値である必要があります
        
        sqrPost(_.identity, 100);
        //=> 100
        
        /*
          事後条件をチェックする関数は、
          _.composeを接着剤として利用して作成することができる
        */
        var megaCheckedSqr = _.compose(partial(sqrPost, _.identity), checkedSqr);
        
        megaCheckedSqr(10);
        //=> 100
        
        megaCheckedSqr(0);
        // Error: 0ではいけません
        
        megaCheckedSqr(NaN);
        // Error: 結果は正の数である必要があります
      

まとめ

• 本章では、既存の関数から新しい関数を合成することができるという考え方を学んだ
  • 最初に説明した合成関数はcurry
  • 2つ目の合成関数はpartial
  • 最後の合成関数はcompose
• 次章では関数型プログラミングでは一般的に使われる再帰手法について学ぶ

6. 再帰

• ただ関数について考えることから、より深い関数型スタイルの理解へつなげることが本章の目的
  • 関数を終了すべき時はいつなのか、なぜそうすると良いのかを再帰関数で学ぶ

自身を呼ぶ関数

• 自身を呼ぶ関数
  • 再帰と関数型プログラミングの関連性
    • 歴史的に、再帰（recursion）と関数型プログラミングは関連したものとして教えられてきた
    • 重要である3つの理由
      • 再帰関数をつかったソリューションは、共通の問題のサブセットに単一の抽象を使用する
      • 再帰は可変の状態を隠蔽することができる
      • 再帰は遅延評価や、無限データ構造の処理を行う手段のひとつである
    • 自己再帰関数を記述する際に考慮すべき条件
      • 
      • 終了条件を知ること
      • どのように1ステップを行うかを決める
      • その1ステップもしくはより小さい問題に、問題を分解する
    • 配列を引数としてとり、要素の数を返すmyLengthの例
      • 基本的な特性
        • サイズを0から開始する
        • 配列をループで走査し、それぞれの要素を走査するたびに1を加える
        • 最後まで走査したら、そのサイズが長さである
      • 再帰を伴った特性
        • もし配列が空であれば、長さは0である
        • 配列の最初の要素を切り取り、残りをmyLengthに渡した実行結果に1を加える
      • myLengthの例

          function myLength(ary) {
            if (_.isEmpty(ary))
              return 0;
            else
              return 1 + myLength(_.rest(ary));
          }
        
          /*
            myLengthの実行結果
          */
          myLength(_.range(10));
          //=> 10
          
          myLength([]);
          //=> 0
          
          myLength(_.range(1000));
          //=> 1000
          
          /*
            再帰関数は与えられた引数そのものを
            編集するべきではない
          */
          var a = _.range(10);
          
          myLength(a);
          //=> 10
          
          a;
          //=> [0,1,2,3,4,5,6,7,8,9]
        

    • 再帰をつかったソリューションをうまく実装するためのヒント
      • 「値は、大きな問題に内包された小さな問題によって組み立てられるものである」と認識すること
      • myLength関数の解決方法
        • 空の配列の長さ（0）に単一の要素を持った配列の長さ（1）をいくつか加えたものとしてみることができる
    • 数値と配列を引数として受け取り、数値で指定された回数だけ配列を繰り返し結合し、新しい配列を返すcycle関数の例
      • cycle関数の例

          function cycle(times, ary) {
            if (times <= 0)
              return [];
            else
              return cat(ary, cycle(times - 1, ary));
          }
          
          cycle(2, [1,2,3]);
          //=> [1, 2, 3, 1, 2, 3]
          
          _.take(cycle(20, [1,2,3]), 11);
          //=> [1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2]
        

    • Underscoreの_.zip関数の逆の動作をするunzip関数の例
      • unzip関数の例

          _.zip(['a', 'b', 'c'], [1, 2, 3])
          //=> [['a', 1], ['b', 2], ['c', 3]]
          
          /*
            まずは配列がとりうる
            基本的な値を考える
          */
          var zipped1 = [['a', 1]]
          
          /*
            zipped1配列の最初の要素を
            終了条件の1番目の配列要素として、
            2つ目の要素を終了条件の2番目の配列の要素とする
          */
          function constructPair(pair, rests) {
            return [
                construct(_.first(pair), _.first(rests)),
                construct(second(pair), second(rests))
              ];
          }
          
          /*
            zipped1と終了条件の配列を使うことによって
            手動でunzipを行うことができる
          */
          constructPair(['a', 1], [[], []]);
          //=> [['a'], [1]]
          
          _.zip(['a', [1]]);
          //=> [['a', 1]]
          
          _.zip.apply(null, constructPair(['a', 1], [[], []]));
          //=> [['a', 1]]
          
          /*
            constructPair関数を使って
            より大きなzip化配列もunzipできる
          */
          constructPair(['a', 1],
            constructPair(['b', 2],
             constructPair(['c', 3], [[], []])
            )
          )
          //=> [['a', 'b', 'c'], [1, 2, 3]]
          
          /*
            再帰関数unzipを
            実装する
          */
          function unzip(pairs) {
            if (_.isEmpty(pairs)) return [[], []];
          
            return constructPair(_.first(pairs), unzip(_.rest(pairs)));
          }
          
          unzip(_.zip([1,2,3],[4,5,6]));
          //=> [[1,2,3],[4,5,6]]
        

  • 再帰を使ったグラフ探索
    • 再帰を使ってエレガントに解くことのできる問題のひとつが、グラフ型データ構造のノード探索
    • JavaScriptに影響を及ぼしたプログラミング言語のグラフの例
      • 
      • nexts関数の例

          var influences = [
            ['Lisp', 'Smalltalk'],
            ['Lisp', 'Scheme'],
            ['Smalltalk', 'Self'],
            ['Scheme', 'JavaScript'],
            ['Self', 'Lua'],
            ['Self', 'JavaScript']
          ];
          
          function nexts(graph, node) {
            if (_.isEmpty(graph)) return [];
          
            var pair = _.first(graph);
            var from = _.first(pair);
            var to = second(pair);
            var more = _.rest(graph);
            
            if (_.isEqual(node, from)) 
              return construct(to, nexts(more, node));
            else
              return nexts(more, node);
          }
          
          nexts(influences, 'Lisp');
          //=> ['Smalltalk', 'Scheme']
        

  • 記録つき深さ優先自己再起探索
    • ノード探索の戦略のひとつに、左側のノードを深く探索してから右側にあるノードを探索していく、深さ優先探索（depth-first search）という方法がある
      • 
      • グラフ内のすべてのノードにアクセスしなくてもよい場合に効果的になる
    • 探索済みのノードの記録を保持するdepthSearch関数の例
      • depthSearch関数について
        • 累積変数（accumulator）を利用する
        • 延々と探索し続けないようにすることができる
          • グラフによっては循環している可能性もあるから
      • depthSearch関数の例

          function depthSearch(graph, nodes, seen) {
            if (_.isEmpty(nodes)) return rev(seen);
          
            var node = _.first(nodes);
            var more = _.rest(nodes);
          
            if (_.contains(seen, node)) return depthSearch(graph, more, seen);
            else
              return depthSearch(
                graph,
                cat(nexts(graph, node), more),
                construct(node, seen)
              );
          }
          
          depthSearch(influences, ["Lisp"], []);
          //=> ['Lisp', 'Smalltalk', 'Self', 'Lua', 'JavaScript', 'Scheme']
          
          depthSearch(influences, ["Smalltalk", "Self"], []);
          //=> ['Smalltalk', 'Self', 'Lua', 'JavaScript']
          
          depthSearch(construct(["Lua", "Io"], influences), ["Lisp"], []);
          //=> ["Lisp", "Smalltalk", "Self", "Lua", "Io", "JavaScript", "Scheme"]
        
        

    • 末尾再帰（自己末尾再帰）
      • depthSearchの再帰は「1ステップ」および「より小さな問題」が再帰呼び出しである
        • 片方もしくは両方が再帰呼び出しの場合、末尾再帰（tail recursion）と呼ばれる
        • 関数内で起こる（終了条件を満たす場合を除いた）最後のアクションが再帰呼び出しであるということ
        • 
      • 末尾再帰関数の最適化に対応している言語であれば、スタックフレームを上書き再利用することでメモリ使用量を抑えられる
        • 関数呼び出しが最後の処理のため、その呼び出しの戻り値がわかれば前の状態は不要になるため
        • （ES6ではProper Tail Calls(PTC)が標準で要求されるようにはなっているが、実際の実装状況はSafariがstrict modeで一部対応しているのみ）
      • 末尾再帰を使ってmyLengthを再実装する
        • 末尾再帰を使って再実装したmyLength関数

            function tcLength(ary, n) {
              var l = n ? n : 0;
              if (_.isEmpty(ary)) return l;
              else return tcLength(_.rest(ary), l + 1);
            }
            
            tcLendth(_.range(10));
            //=> 10
          

  • 再帰と関数合成: 論理積と論理和
    • 2つの新しいコンビネータを作ってみる
      • andifyとorifyという再帰関数を実装する
        • andify関数とorify関数

            /*
              andify関数
            
              任意の数のプレディケート関数を、
              ローカル関数everythingで消費している
              これは再帰呼び出しで累積変数を隠蔽するために
              よく使われる手法である
            
              論理積演算子(&&)は遅延評価（short circuiting）を行うため、_.everyがfalseの場合は
              再帰呼び出しは行われない
            */
            function andify(/* 任意の数のプレディケート関数 */) {
              var preds = _.toArray(arguments);
            
              return function (/* 任意の数の引数 */) {
                var args = _.toArray(arguments);
            
                var everything = function (ps, truth) {
                  if (_.isEmpty(ps)) return truth;
                  else return _.every(args, _.first(ps)) && everything(_.rest(ps), truth);
                };
            
                return everything(preds, true);
              };
            }
            
            var evenNums = andify(_.isNumber, isEven);
            
            evenNums(1, 2);
            //=> false
            
            evenNums(2, 4, 6, 8);
            //=> true
            
            evenNums(2, 4, 6, 8, 9);
            //=> false
            
            /*
              orify関数
            
              andify関数の実装とほぼ同じ
            */
            function orify(/* 任意の数のプレディケート関数 */) {
              var preds = _.toArray(arguments);
            
              return function (/* 任意の数の引数 */) {
                var args = _.toArray(arguments);
            
                var something = function (ps, truth) {
                  if (_.isEmpty) return truth;
                  else return _.some(args, _.first(ps)) || something(_.rest(ps), truth);
                };
            
                return something(preds, false);
              };
            }
            
            var zeroOrOdd = orify(isOdd, zero);
            
            zeroOrOdd();
            //=> false
            
            zeroOrOdd(0, 2, 4, 6);
            //=> true
            
            zeroOrOdd(2, 4, 6);
            //=> false
          

  • 相互再帰関数（自身を呼ぶ他の関数を呼ぶ関数）
    • 2以上の関数がお互いを呼び合う状態を相互再帰（mutual recursion）という
      • 
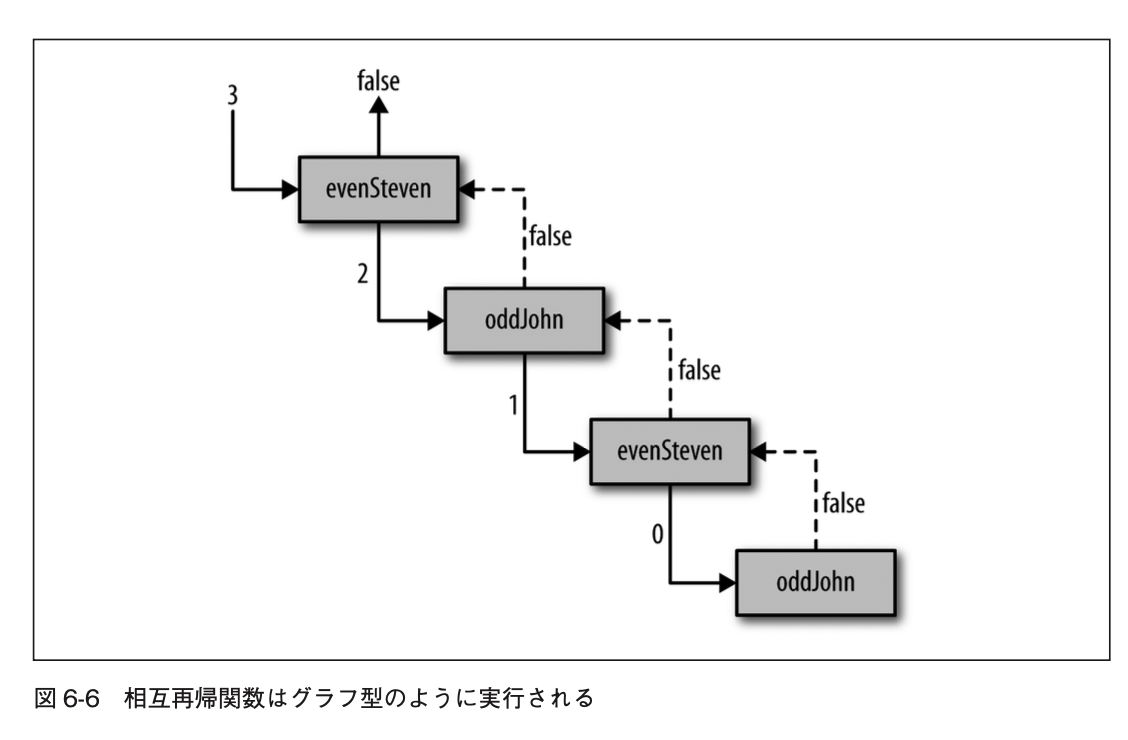
      • 奇数偶数を判断する2つの関数を実装する
      • 相互再帰関数の例

          /*
            お互いの間を行き来して、
            どちらかの関数で0に到達するまで
            絶対値を1ずつ減らす関数
          */
          function evenSteven(n) {
            if (n === 0) return true;
            else return oddJohn(Math.abs(n) - 1);
          }
          
          function oddJohn(n) {
            if (n === 0) return false;
            else return evenSteven(Math.abs(n) - 1);
          }
          
          evenSteven(4);
          //=> true
          
          oddJohn(11);
          //=> true
          
          /*
            高階関数を利用するとしたら
            関数が自身を_.map関数に引数として
            渡して呼び出す再帰関数がある
          
            （この相互再帰の例は実際に使用す流にはあまり適していない）
          */
          function flat(array) {
            if (_.isArray(array)) return cat.apply(cat, _.map(array, flat));
            else return [array];
          }
          
          flat([
            [1, 2],
            [3, 4],
          ]);
          //=> [1, 2, 3, 4]
          
          flat([
            [1, 2],
            [3, 4, [5, 6, [[[7]]], 8]],
          ]);
          //=> [1,2,3,4,5,6,7,8]
        

  • 再帰を使った深いコピー
    • オブジェクトの深いコピーは再帰がぴったりとはまる

    •   /*
          deepColne関数は
          再帰を使って深いコピーを実現できる
        
          （本番環境で使えるほど堅固なものではない）
        */
        function deepClone(obj) {
          if (!existy(obj) || !_.isObject(obj)) return obj;
        
          var temp = new obj.constructor();
          for (var key in obj)
            if (obj.hasOwnProperty(key)) temp[key] = deepClone(obj[key]);
        
          return temp;
        }
        
        var x = [{ a: [1, 2, 3], b: 42 }, { c: { d: [] } }];
        var y = deepClone(x);
        
        _.isEqual(x, y);
        //=> true
        
        y[1]["c"]["d"] = 42;
        
        _.isEqual(x, y);
        //=> false
      

  • ネストされた配列を探索する
    • ネストされた配列を持った配列の探索は、頻繁に必要とされることがある
    • 深さ優先探索をおこなう関数の例

        /*
          ネストされた配列を持った
          配列の探索のよくある例
        */
        doSomethingWithResult(_.map(someArray, someFuntion));
        
        /*
          上記のパターンは十分に一般的であるため、
          抽象化することができる
        */
        function visit(mapFun, resultFun, array) {
          if (_.isArray(array)) {
            return resultFun(_.map(array, mapFun));
          } else {
            // arrayが配列でない場合の処理を書くことで、部分適用で役に立つ
            return resultFun(array);
          }
        }
        
        visit(_.identity, _.isNumber, 42);
        //=> true
        
        visit(_.isNumber, _.identity, [1, 2, null, 3]);
        //=> [true, true, false, true]
        
        visit(
          function (n) {
            return n * 2;
          },
          rev,
          _.range(10)
        );
        //=> [18, 16, 14, 12, 10, 8, 6, 4, 2, 0]
        
        /*
          visit関数を使った相互再帰バージョンの
          depthSearchを実装できる
          これをpostDepthと名付ける
        
          この関数は子要素を展開した後に
          mapFunを実行して、深さ優先探索を行う
        */
        function postDepth(fun, ary) {
          return visit(partial1(postDepth, fun), fun, ary);
        }
        
        /*
          preDepth関数は
          子要素を展開する前にmapFunを実行する
        */
        function preDepth(fun, ary) {
          return visit(partial1(preDepth, fun), fun, fun(ary));
        }
        
        /*
          _.identity関数を渡すと、
          influences配列のコピーを返す
        */
        postDepth(_.identity, influences);
        //=> [['Lisp', 'Smalltalk'], ['Lisp', 'Scheme'], ...
        
        /*
          Listをすべて大文字のLISTに
          置き換える
        */
        postDepth(function (x) {
          if (x === "Lisp") {
            return "LISP";
          } else {
            return x;
          }
        }, influences);
        //=> [['LISP', 'Smalltalk'], ['LISP', 'Scheme'], ...
        
        /*
          もちろん元の配列は
          変更されない
        */
        influences;
        //=> [['Lisp', 'Smalltalk'], ['Lisp', 'Scheme'], ...
        
        /*
          ある言語が影響を及ぼした言語の配列を
          生成したい場合
        */
        function influencedWithStrategy(strategy, lang, graph) {
          var results = [];
        
          strategy(function (x) {
            if (_.isArray(x) && _.first(x) === lang) {
              results.push(second(x));
            }
        
            return x;
          }, graph);
        
          return results;
        }
        
        influencedWithStrategy(postDepth, "Lisp", influences);
        //=> ['Smalltalk', 'Scheme']
      

再帰多すぎ！（トランポリンとジェネレータ）

• 再帰多すぎ問題
  • 現在のJavaScriptエンジンは再帰呼び出しの最適化は行わない
    • ほとんどのJavaScriptエンジンは再起の回数に制限を設けている
      • エラーが発生することがある
      • evenStevenとoddJohnのように0に到達するまで何万回も相互再帰を繰り返す関数はエラーが起こる
  • トランポリンとは
    • エラーを取り除くトランポリン（trampoline）という制御構造がある
      • 深くネストされた再帰呼び出しの代わりに、トランポリンが呼び出しを平坦化する
    • まず相互再帰関数がスタックを破壊しないように手動で修正してみる
      • 直接呼ばずに、呼び出しをラッピングする関数を返すようにしてみることから始める
      • trampoline関数

          evenSteven(100000);
          // 多すぎる再帰（もしくはそれに起因するエラー）が発生する
          
          /*
            実行部で相互再帰関数を呼び合う代わりに、
            呼び出しをラッピングした関数を返す
          */
          function even0line(n) {
            if (n === 0) {
              return true;
            } else {
              return partial1(odd0line, Math.abs(n) - 1);
            }
          }
          
          function odd0line(n) {
            if (n === 0) {
              return false;
            } else {
              return partial1(even0line, Math.abs(n) - 1);
            }
          }
          
          even0line(0);
          //=> true
          
          odd0line(0);
          //=> false
          
          /*
            手動で再帰構造を
            平坦化してみる
          */
          odd0line(3);
          //=> function () { return even0line(Math.abs(n) - 1); }
          
          odd0line(3)();
          //=> function () { return odd0line(Math.abs(n) - 1); }
          
          odd0line(3)()();
          //=> function () { return even0line(Math.abs(n) - 1); }
          
          odd0line(3)()()();
          //=> true
          
          odd0line(200000001)()()();
          //=> true
          
          /*
            このような呼び出しの平坦化処理を
            プログラムで行うtrampolineという関数を作成する
          
            trampolien関数は、関数funの戻り値が関数でなくなるまで、
            その関数をひたすら呼び出し続ける
          */
          function trampoline(fun /*, 任意の数の引数 */) {
            var result = fun.apply(fun, _.rest(arguments));
          
            while (_.isFunction(result)) {
              result = result();
            }
          
            return result;
          }
          
          trampoline(odd0line, 3);
          //=> true
          
          trampoline(even0line, 200000);
          //=> true
          
          trampoline(odd0line, 300000);
          //=> false
          
          trampoline(even0line, 200000000);
          //=> true
          
          /*
            この仕組みを関数の内部に
            完全に隠蔽することもできる
          */
          function isEvenSafe(n) {
            if (n === 0) {
              return true;
            } else {
              return trampoline(partial1(odd0line, Math.abs(n) - 1));
            }
          }
          
          function isOddSafe(n) {
            if (n === 0) {
              return false;
            } else {
              return trampoline(partial1(even0line, Math.abs(n) - 1));
            }
          }
          
          isOddSafe(2000001);
          //=> true
          
          isEvenSafe(2000001);
          //=> false
        

  • ジェネレータ（generators）
    • トランポリンの性質を利用して無限を扱う例
      • 再帰を使用して無限の遅いデータストリームを構築して処理する
        • 計算する必要が生じるまで計算しない
      • 関数を相互に呼び出し合う
    • ジェネレータ関数の例

        /*
          cycle関数では、11個の要素を取得するために
          60個の要素を生成してしまっている非効率がある
        */
        _.take(cycle(20, [1, 2, 3]), 11);
        //=> [1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2]
        
        /*
          配列は最初の要素（頭）と、それ以降のすべての要素（尾）によって
          構成されるものであるという考え方を利用して、
          無限の要素を持つ配列も同様に表現できる
        */
        // {head: aValue, tail: ???};
        
        /*
          odd0lineの例を使うと、
          tailの値には、尾を計算する関数が入ることがわかる
          そしてこの尾は再帰関数である
        
          頭/尾のオブジェクトには2つの関数が必要となる
          1. 現在の要素の値を計算する関数
          2. 次の要素のシードとなる値を計算する関数
        
          これはジェネレータと呼ばれる形態である
        
          currentには頭の値を計算する関数が渡され、
          stepには再帰呼び出しに渡す値を計算する関数が渡される
          tailは関数であり、呼び出されるまでは実際の値ではない
        */
        function generator(seed, current, step) {
          return {
            head: current(seed),
            tail: function () {
              console.log("forced");
              return generator(step(seed), current, step);
            },
          };
        }
        
        /*
          ジェネレータを操縦するために
          ユーティリティ関数（アクセサ関数）を定義する
        
          genHeadとgenTailは、それぞれ頭と尾を返す
          genTailの戻り値は強制的に生成された尾の値となる
        */
        function genHead(gen) {
          return gen.head;
        }
        function genTail(gen) {
          return gen.tail();
        }
        
        var ints = generator(0, _.identity, function (n) {
          return n + 1;
        });
        
        genHead(ints);
        //=> 0
        
        genTail(ints);
        // (console) forced
        //=> {head: 1, tail: function () {...}}
        
        /*
          genTailは強制的に計算を行うので、
          ネストして実行すると、ネスト数に応じてジェネレータに
          強制的に計算を行わせることができる
        */
        genTail(genTail(ints));
        // (console) forced
        // (console) forced
        //=> {head: 2, tail: function () {...}}
        
        /*
          2つの関数を使うことで、
          より強力なアクセサ関数genTakeを
          組み立てることができる
        
          genTakeはジェネレータの最初のn個の値を
          配列に格納して返す
        */
        function genTake(n, gen) {
          var doTake = function (x, g, ret) {
            if (x === 0) {
              return ret;
            } else {
              return partial(doTake, x - 1, genTail(g), cat(ret, genHead(g)));
            }
          };
        
          return trampoline(doTake, n, gen, []);
        }
        
        /*
          トランポリンの原則を使って、
          再帰でスタックを破壊せずにオンデマンドで値を計算する、
          無限のサイズを持った構造体を定義できることは
          面白い
        
          ただ、たとえトランポリンを利用してコールスタックの破綻を
          防ぐことはできたとしても、その問題をヒープ領域に押し付けたに
          すぎない
          しかしJavaScriptではヒープ領域のサイズはコールスタックよりも
          数桁大きいため、メモリ消費量による問題が発生する可能性は
          低くなる
        
          トランポリンを直接利用するというよりは、JavaScriptにおいては
          トランポリンの考え方自体が意識しておくべき一般的な原則と言える
        */
        genTake(10, ints);
        // (console) forced x 10
        //=> [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
        
        genTake(100, ints);
        // (console) forced x 100
        //=> [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, ..., 98, 99]
        
        genTake(1000, ints);
        // (console) forced x 1000
        //=> [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, ..., 998, 999]
        
        genTake(10000, ints);
        // (console) forced x 10000
        //=> [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, ..., 9998, 9999]
        
        genTake(100000, ints);
        // (console) forced x 100000
        //=> [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, ..., 99998, 99999]
        
        genTake(1000000, ints);
        // (console) forced x 1000000
        //=> [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, ..., 999998, 999999]
        
        /*
          generator関数によって生成されたジェネレータは、
          尾の要素はアクセスされるまで計算はされないが、
          アクセスされるたびに毎回計算が行われてしまうという
          致命的な欠陥がある
        */
        genTake(10, ints);
        // (console) forced x 10
        //=> [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
      

  • トランポリンの原則とコールバック
    • setTimeoutやXMLHttpRequestのような非同期APIは、再帰に関連した面白い性質を持っている
      • 非同期ライブラリはノンブロッキングのイベントループを利用している
      • ノンブロッキングAPIとは
        • 非同期APIを使って長い実行時間がかかる関数の実行をスケジュールする場合
          • ブラウザもしくはJavaScriptのランタイムはその関数の実行終了を待つかたわら、プログラムの実行自体をブロックせずに他の処理を先に進める
          • その代わりに、非同期APIは関数の処理終了時に呼び出されるコールバック（単なる関数もしくはクロージャ）を持っている
        • これにより、即時処理されるものでも時間がかかる処理でもアプリケーションの操作をブロックすることなく実質的な並行処理を行うことができる
        • ノンブロッキングAPIの特徴として、関数呼び出し自体はコールバックが呼ばれる前に終了して、値を返すようになっている
          • その後、コールバックが実行される
      • イベントループと再帰の性質の例

          setTimeout(function () {
            console.log("hi");
          }, 2000);
          //=> 何かしらの値をすぐに返す
          // ...2秒後
          // (console) hi
          
          /*
            なんらかの値を返すことについて、
            イベントループのそれぞれの新しいtickのたびに
            コールスタックを白紙に戻すのが興味深い点となる
            （tick: イベントループ内でタイミングを刻むステップの単位）
          
            非同期コールバックは常にイベントループの新しいtickで呼ばれるため、
            再帰関数も白紙状態のコールスタックで実行される
          
            $.get関数が失敗した場合にlooper関数へ再帰呼び出しが行われる例
          */
          function asyncGetAny(interval, urls, onsuccess, onfailure) {
            var n = urls.length;
            var looper = function (i) {
              setTimeout(function () {
                if (i >= n) {
                  onfailure("failed");
                  return;
                }
                $.get(urls[i], onsuccess)
                  .always(function () {
                    console.log("try: " + urls[i]);
                  })
                  .fail(function () {
                    looper(i + 1);
                  });
              }, interval);
            };
            looper(0);
            return "go";
          }
          
          var urls = [
            "http://doesNotExist_.com",
            "http://doesNotExist2_.biz",
            "_.html",
            "foo.txt",
          ];
          
          asyncGetAny(
            2000,
            urls,
            function (data) {
              alert("データが見つかりました");
            },
            function (data) {
              console.log("すべて失敗しました");
            }
          );
          
          //=> "go"
          // (console) try: http://doesNotExist_.com
          // (console) try: http://doesNotExist2_.biz
          // (console) try: _.html
          // (console) try: foo.txt
          // (ファイルが存在する場合) alert("データが見つかりました")
        

再帰は低レイヤーでの操作

• 再帰は低レイヤーでの操作
  • 再帰の注意点
    • 低レイヤーでの操作なので、可能な場合は避けたほうがよい
      • 利用できる高階関数を調べて、それらを組み合わせて新しい関数を生成する
  • すでに存在する関数を組み合わせることで、再帰と同様の効果を実現する
    • influencedWithStrategy関数の例
    • influencedWithStrategy関数の例

        var groupFrom = curry2(_.groupBy)(_.first);
        var groupTo = curry2(_.groupBy)(second);
        
        groupFrom(influences);
        //=> {Lisp: [['Lisp', 'Smalltalk'], ['Lisp', 'Scheme']],
        //    Smalltalk: [['Smalltalk', 'Self']],
        //    Scheme: [['Scheme', 'JavaScript']],
        //    Self: [['Self', 'Lua'], ['Self', 'JavaScript']]}
        
        groupTo(influences);
        //=> {Smalltalk: [['Lisp', 'Smalltalk']],
        //    Scheme: [['Lisp', 'Scheme']],
        //    Self:[[Smalltalk', 'Self']],
        //    JavaScript: [['Scheme', 'JavaScript'], ['Self', 'JavaScript']],
        //    Lua:[['Scheme', 'Lua'][['Self', 'Lua']]}
        
        /*
          influenced関数は再帰を使わずに、
          ある言語が影響を与えた言語を取得することができる
        
          _.groupBy, _.first, second, _.mapの挙動を
          それぞれ知っているため、データがそれぞれの関数によって
          どのように変換されるかを理解するだけで、influenced関数の
          実装内容を理解することができる
          これこそが関数型プログラミングの大きな利点である
        
          レゴブロックのようにパーツを組み合わせて、データフローとデータ変換を
          パイプラインに乗せて、望む通りの最終形を導き出すことができる
        */
        function influenced(graph, node) {
          return _.map(groupFrom(graph)[node], second);
        }
        
        influencedWithStrategy(postDepth, "Lisp", influences);
        //=> ['Smalltalk', 'Scheme']
        
        influenced(influences, "Lisp");
        //=> ['Smalltalk', 'Scheme']
      

まとめ

• 本章は再帰関数を扱った
  • 自身を呼び出す関数は、ネストされたデータ構造の探索と操作のための強力なツールとなる
    • 深さ優先探索を行うvisit関数を用いて、木構造を探索する例
  • 木構造の探索は強力なテクニックだが、JavaScriptでの再帰の回数制限に引っかかる可能性があった
    • トランポリンを使用することで、クロージャの配列を通じてお互いを呼び合う関数を構築する方法を学んだ
  • 再帰は控えめに使うべきであるという話をした
    • 再帰関数は、高階関数や合成された関数よりも複雑であり直感的でない
    • 極力関数合成を使用して、再帰やトランポリンは必要な場合のみ使用することが一般的な考え方
  • 次はその場で変更する動作・変異（mutation）を説明する

7. 純粋性、不変性、変更ポリシー

• 本章では、関数型かつ実用的なスタイルを求めるための要点を説明する
  • 関数型プログラミングとは、関数で構築するプログラミングスタイルだけではない
    • ソフトウェアの創造プロセスにまとわりつく複雑さを最小限に抑えるための構築方法を考える手段である
  • 複雑さを抑えるひとつの方法
    • プログラム内の状態変更を最小限に抑えること
    • もしくは、完全に排除すること

純粋性

• 純粋性
  • ある数値を与えられると、1からその数値までの間から（疑似）ランダムに選んだ数値を返すような関数を考えてみる
    • rand関数

        var rand = partial1(_.random, 1);
        
        rand(10);
        //=> 7
        
        repeatedly(10, partial1(rand, 10));
        //=> [7, 3, 9, 10, 5, 6, 2, 5, 10, 7]
        
        _.take(repeatedly(100, partial1(rand, 10)), 5);
        //=> [7, 3, 9, 10, 5]
        
        function randAtring(len) {
          var ascii = repeatedly(len, partial1(rand, 36));
        
          return _.map(ascii, function (n) {
            return n.toString(36);
          }).join("");
        }
        
        randString(0);
        //=> ""
        
        randString(1);
        //=> "b"
        
        randString(10);
        //=> "3lq6w7o1b3"
      

    • randStringはこれまで組み立ててきた関数と同様だが、大きな違いがある
      • 「あなたはこれをテストできますか？」という質問が答えの一部となる
  • 純粋性とテストの関係
    • randString関数の呼び出し結果を予測する手段が存在しないという問題がある
      • randString関数のテストの考察

          /*
            randString関数は、
            呼び出し結果を予測できない
          */
          describe("randString", function() {
            iterateUntil("builds a string of lowercase ASCII letters/digits", function() {
              expect(randString()).to???(???);
            })
          })
          
          /*
            _.map関数は、
            与えられた引数によって実行結果が決まるため、
            純粋な関数となる
          */
          describe("_.map", function () {
            it("should return an array made from...", function () {
              expect(_.map([1,2,3], sqr)).toEqual([1, 4, 9]);
            })
          })
        

    • 純粋な関数の性質
      • 結果は引数として与えられた値からのみ計算される
        • コントロールできる範囲の外のデータに頼るような関数を書くことは、混乱を発生させることがあるから
        • 純粋性のルールの則ると、テストがより簡単になるだけでなく、一般的に理解しやすいプログラムを書くことの助けにもなる
      • 関数の外部で変更される可能性のあるデータに一切依存しない
      • 関数実行部の外側に存在する何かの状態を一切変更しない
    • 純粋性を破る例
      • PIの値が変わってしまう例

          /*
            1つ目の純粋性を破る例
          */
          PI = 3.14;
          
          function areaOfACircle(radius) {
            return PI * sqr(radius);
          }
          
          areaOfACircle(3);
          //=> 28.26
          
          // ...ライブラリのコード
          PI = "Magnum";
          
          // ...続き
          areaOfACircle(3);
          //=> NaN
          // JavaScriptは実行時に任意のコードを呼び出して、
          // オブジェクトや変数の内容を簡単に書き換えることができてしまう
        

純粋と不純を分離する

• 純粋と不純を分離する
  • 純粋性を損なう原因となるJavaScriptのメソッドや関数などがある
    • Date.now, console.log, Math, thisやグローバル変数の使用など
    • JavaScriptは参照でオブジェクトの受け渡しを行うため、オブジェクトもしくは配列を引数の取るすべての関数が純粋性を損なう可能性を持っている
    • しかし、これらの問題は低減することができる
    • JavaScriptは決して完全な純粋性を持つことはない（そもそもそれは必要とされていない）が、変更の影響は最小化できるということ
  • randString関数は不純だが、純粋な部分を不純な部分から切り離してコードを再構築する方法がある
    • 文字生成部分と、文字結合して文字列を生成する部分の2つに分割できる
      • 2つの関数を生成すればよい
      • randString関数を2つの関数に分けた例

          function generateRandomCharacter() {
            return rand(26).toString(36); // 説明上の意図的な誤りが含まれている
          }
          
          function generateString(charGen, len) {
            return repeatedly(len, charGen).join("");
          }
          
          generateString(generateRandomCharacter, 20);
          //=> "3lq6w7o1b3..."
          
          var composedRandomString = partial1(generateString, generateRandomCharacter);
          
          composedRandomString(10);
          //=> "aeq6fdsafw"
          
          describe("generateString", function () {
            var result = generateString(always("a"), 10);
          
            it("特定の長さを持った文字列を返す", function () {
              expect(result.constructor).toBe(String);
              expect(result.length).toBe(10);
            });
          
            it("文字生成関数が返す文字に合致する", function () {
              expect(result).toEqual("aaaaaaaaaa");
            });
          });
        

  • 不純関数を適切にテストする
    • 関数が不純であり、関数外の条件に戻り値が依存する場合、どのようにテストできるか？
      • 戻り値の一定の特徴についてはテストできる
      • generateRandomCharacterの例
        • ASCII文字であること
        • 1桁の数値であること
        • 文字列型であること
        • 文字であること
        • 小文字であること
    • ただ、特徴をテストするためには大量のデータが必要となってしまう
      • 大量のデータが必要となるテストの例

          /*
            10000程度の実行程度では完全なテストとは言えないが、
            反復回数を増やしても完全に満たされることはない
          
            また、生成される文字が一定の範囲内の文字であることを
            確認する必要もあるし、そもそもgenerateRandomCharacter関数では
            すべての可能な小文字のASCII文字を生成できない
          
            そうなると、このテストはランダム性を持つ関数に対しては
            あまり意味を持たなくなってしまう
          */
          describe("generateRandomCharacter", function () {
            var result = repeatedly(10000, generateRandomCharacter);
          
            it("長さ1の文字列を返す", function () {
              expect(_.every(result, _.isString)).toBeTruthy();
              expect(
                _.every(result, function (s) {
                  return s.length === 1;
                })
              ).toBeTruthy();
            });
          
            it("アルファベットの小文字か数字を返す", function () {
              expect(
                _.every(result, function (s) {
                  return /[a-z0-9]/.test(s);
                })
              ).toBeTruthy();
          
              expect(
                _.any(result, function (s) {
                  return /[A-Z]/.test(s);
                })
              ).toBeFaly();
            });
          });
        

  • 純粋性と参照透過性との関係
    • JavaScriptは非常に動的な言語だが、型付けに対する緩さを柔軟性と捉えて上手に活用することもできる
      • 型付けに対する緩さの例: true + 1 === 2
      • 純粋関数を使えば、関数の合成が簡単になり、テストも容易になる
    • second関数を定義する際のnth関数の利用方法の例
      • nth関数の例

          function second(a) {
            return nth(a, 1);
          }
          
          /*
            nthは純粋関数なので、
            与えられる配列とインデックス番号が同じであれば
            常に同じ値を返す（参照透過性）
          */
          nth(["a", "b", "c"], 1);
          //=> 'b'
          
          nth(["a", "b", "c"], 1);
          //=> 'b'
          
          /*
            次に、nth関数は
            引数として与えられた配列を変更しない
          */
          var a = ["a", "b", "c"];
          
          nth(a, 1);
          //=> 'b'
          
          a === a;
          //=> true
          
          nth(a, 1);
          //=> 'b'
          
          _.isEqual(a, ["a", "b", "c"]);
          //=> true
          
          /*
            JavaScriptと付き合っていく上で
            避けて通れない唯一の制限事項としては、
            nth関数は不純なものを返す可能性があるということである
          */
          
          nth([{ a: 1 }, { b: 2 }], 0);
          //=> {a: 1}
          
          nth(
            [
              function () {
                console.log("blah");
              },
            ],
            0
          );
          //=> function ...
          
          /*
            この問題への対処法としては、
            不純な部分を明示的に最小化できる場合を除いて、
            引数値を変更することや外部の値に頼らない
            純粋関数だけを定義し、使用するように
            気をつけることが重要である
          
            関数の純粋性を保つためには自身を律することを
            要求されるが、それによりプログラミングの幅を広げることができる
          
            たとえば、second関数の実行部をそれと同等の値と
            入れ替えてしまうこともできるようになる
          */
          function second(a) {
            return a[1];
          }
          
          function second(a) {
            return _.first(_.rest(a));
          }
          
          /*
            nthは純粋関数なので、
            置き換えの影響はほとんどない
          
            nth関数に任意の配列を与えた場合の
            結果の値を関数自体と置き換えても
            プログラムの一貫性は保たれる
          */
          function second() {
            return "b";
          }
          
          second(["a", "b", "c"], 1);
          //=> 'b'
        

    • 状態変異がもたらす混乱なしで、新しい関数に自由に入れ替えることができる
      • これはプログラミングにおける「自由」でもある
  • 純粋性と冪等性の関係
    • 冪等性とは
      • RESTfulなAPIやアーキテクチャが流行するにしたがって、冪等性（idempotence）の考え方が一般に浸透した
      • あるアクションを何度行っても一度行った場合とまったく同じ効果をもたらすこと
    • 関数型プログラミングにおける冪等性は、純粋性と関連しているが異なるものである
      • 冪等である関数の例
        • 冪等である関数の例

            /*
              冪等である関数は、
              次の条件を満たす
            
              つまり、ある引数を与えて関数を実行するということは、
              その関数を2回連続で実行しても同じ結果を返すということである
            */
            someFun(arg) == _.compose(someFun, someFun)(arg);
            
            /*
              second関数は冪等ではない
            */
            var a = [1, [10, 20, 30], 3];
            
            var secondTwice = _.compose(second, second);
            
            second(a) === secondTwice(a);
            //=> false
            // second関数は[10, 20, 30]を返すが、
            // secondTwice関数は20を返す
            
            /*
              一番直接的な冪等関数は
              _.identity関数である
            */
            var dissociativeIdentity = _.compose(_.identity, _.identity);
            
            _.identity(42) === dissociativeIdentity(42);
            //=> true
            
            /*
              Math.abs関数も冪等関数である
            */
            Math.abs(Math.abs(-42));
            //=> 42
          

    • 変数について
      • 変数を変更するたびに、その変数の参照するタイミングによって異なる値が返される可能性が発生していると認識する
        • 変更される変数が、クロージャにカプセル化されているか、コンテナオブジェクトに格納されているかは関係ない
        • プログラム実行中の任意の時点において、その状態は、微妙な変更作用の発生に左右されてしまうということ
      • プログラムのすべての状態変更を除去することはできないが、可能な限り減らす方がよい
        • 不変性とは、状態変更が存在しないという性質のことである

不変性

• 不変性
  • 不変性とは

    • JavaScriptには、デフォルトで不変性（immutability）を持つデータ型はほとんど存在しない

      • 文字列型は不変性を持った数少ないデータ型のひとつ
      • 文字列型の不変性の例

          var s = "Lemongrab";
          
          s.toUpperCase();
          //=> "LEMONGRAB"
          
          s;
          //=> "Lemongrab"
          
          /*
            文字列型が不変でない場合に
            起こりうる混乱の例
          */
          var key = "lemongrab";
          var obj = { lemongrab: "Earl" };
          
          obj[key] === "Earl";
          //=> true
          
          // 架空の関数がkey変数の文字列を"lemonjon"に変更するとする
          doSomethingThatMutatesStrings(key);
          
          obj[key];
          //=> undefined
          
          obj["lemonjon"];
          //=> "Earl"
          // (実際にはundefined)
          
          /*
            JavaScriptでは
            下記の変異は許容されている
          */
          var obj = { lemongrab: "Earl" };
          
          (function (o) {
            _.extend(o, { lemongrab: "King" });
          })(obj);
          
          obj;
          //=> {lemongrab: "King"}
        
        

    • プログラムが大きくなると変異点によって生成された依存関係が拡大していく

      • 変異点への影響のあるすべての変更が、依存関係を広範囲に撹乱してしまうようになる
      • どのような変更でも全体に影響が及ぶようになってしまう

    • 関数型プログラミングにおける理想の状況は、可変なものがまったく存在しないという状況

      • 不変性を中心に据えた制限的なポリシーでプログラミングを始めると、結果的にできることが増えるようになる
        • 不変性の美徳
  • 誰もいない森で木が倒れたら、音がするでしょうか？
    • skipTakeの例
      • forループを使ったskipTakeの例

          function skipTake(n, coll) {
            var ret = [];
          
            var sz = _.size(coll);
            for (var index = 0; index < sz; index += n) {
              ret.push(coll[index]);
            }
            return ret;
          }
          
          skipTake(2, [1, 2, 3, 4]);
          //=> [1, 3]
          
          skipTake(3, _.range(20));
          //=> [0, 3, 6, 9, 12, 15, 18]
        

    • skipTakeには、配列を変異させるArray#pushを含んだ命令型スタイルのループが入っている
      • 関数型プログラミングのテクニックを使ってskipTakeを実装する方法もある
      • だが、forループを使った実装はシンプルで小さく、動作も速い
      • 重要な点は、命令型アプローチを使っている事実がskipTake関数を使用する者に対して完全に隠蔽されていること
        • 関数を抽象の基本的なユニットとしてみる利点は、その実装内容さえ漏れることがなければ、関数内部の詳細な実装方法はまったく無関係になるということ
        • skipTakeの中で_.reduceRightを使おうが、whileを使おうが、関数の利用者にとっては無関係なこととなる
        • 関数は変異を隠蔽するための便利な境界を提供してくれる

    • 誰もいない森で木が倒れたら、音がするでしょうか？不変性を持った戻り値を生成するために純粋関数がローカルデータを変異させたとしたら、それは問題ないのでしょうか？ --- Rich Hickey http://clojure.org/transients

      • この答えはYesとなる
  • 不変性と、その再帰との関係
    • 関数型プログラミングを説明した本に必ず再帰が出てくるのは、それが純粋性と関係しているから
      • 多くの関数型プログラミング言語では、ローカル変数の変異を用いたsummのような関数を書くことができない
        • JavaScriptが、再帰による状態管理も、ローカル変数による変異も許容するのであれば、速く動く方を使わない手はない
      • summ関数の例

          /*
            summ関数は、
            iとresultという2つのローカル変数を
            変異させている
          
            伝統的な関数型言語では、
            変数の再代入は許されていない
          */
          function summ(array) {
            var result = 0;
            var sz = array.length;
          
            for (var i = 0; i < sz; i++) {
              result += array[i];
            }
            return result;
          }
          
          summ(_.range(1, 11));
          //=> 55
          
          /*
            このsumm関数を純粋関数に変更するためには、
            コールスタックを介して変更する必要がある
          
            再帰によって、関数の引数（seed）を通じて
            状態が管理され、状態の変更はある再帰呼び出しの引数が
            次の呼び出しに渡されることで行われるようになる
          */
          function summRec(array, seed) {
            if (_.isEmpty(array)) {
              return seed;
            } else {
              return summRec(_.rest(array), _.first(array) + seed);
            }
          }
          
          summRec([], 0);
          //=> 0
          
          summRec(_.range(1, 11), 0);
          //=> 55
        

  • 防御的フリーズとクローン
    • JavaScriptの配列やオブジェクトは参照渡しであるため、本当に不変なものは存在しない
    • 変更を無効にするObject#freezeは提供されている
      • Object#freezeを使用した不変性の確保の問題
        • コードベース全体をコントロールできる立場にいないと、微妙なエラーを発生させる可能性がある
        • Object#freezeはあくまで浅いフリーズである
        • Object.freeze関数の例

            var a = [1, 2, 3];
            a[1] = 42;
            
            a;
            //=> [1, 42, 3]
            
            Object.freeze(a);
            
            /*
              Object.freeze関数を
              呼び出した後は、配列の変更ができなくなる
            */
            a[1] = 108;
            
            a;
            //=> [1, 42, 3]
            
            Object.isFrozen(a);
            //=> true
            
            /*
              オブジェクトをフリーズさせて、それを
              任意のAPIに自由に渡してしまうと、
              トラブルになる可能性がある
            
              また、ネストされたオブジェクトは
              フリーズされない
            */
            var x = [{ a: [1, 2, 3], b: 42 }, { c: { d: [] } }];
            
            Object.freeze(x);
            
            x[0] = "";
            
            x;
            //=> [{a: [1,2,3], b: 42}, {c: {d: []}}];
            
            x[1]["c"]["d"] = 1000000;
            
            x;
            //=> [{a: [1,2,3], b: 42}, {c: {d: 1000000}}];
            
            /*
              深いフリーズを行う場合は、
              deepClone関数のように、再帰を使って
              データ構造を探索する必要がある
            */
            function deepFreeze(obj) {
              if (!Object.isFrozen(obj)) {
                Object.freeze(obj);
              }
            
              for (var key in obj) {
                if (!obj.hasOwnProperty(key) || !_.isObject(obj[key])) {
                  continue;
                }
            
                deepFreeze(obj[key]);
              }
            }
            
            var x = [{ a: [1, 2, 3], b: 42 }, { c: { d: [] } }];
            
            deepFreeze(x);
            x[0] = null;
            
            x;
            //=> [{a: [1,2,3], b: 42}, {c: {d: []}}];
            
            x[1]["c"]["d"] = 42;
            
            x;
            //=> [{a: [1,2,3], b: 42}, {c: {d: []}}];
          

      • よって、フリーズは極力避けるべきだと言える
    • 普遍性を保つためにとりうる手段は3点に限定される
      • 浅いコピーで十分な場合は、_.cloneを使ってコピーする
      • 深いコピーが必要な場合は、deepCloneを使う
      • 純粋関数を使ってコードを記述する
  • 関数レベルの不変性を意識する
    • 本書で定義した関数とUnderscoreが提供する関数の多くは共通の特徴を持っている
      • コレクションを引数にとり、別のコレクションを構築するということ
    • 純粋でない関数を合成可能にする例
      • 数値または文字列の配列を引数に取り、配列のそれぞれの要素をキーに、要素が配列に登場した回数をフィールドの値としたオブジェクトを返す関数の例
      • 純粋でないextend関数を合成可能にする例

          var freq = curry2(_.countBy)(_.identity);
          
          var a = repeatedly(1000, partial1(rand, 2));
          var copy = _.clone(a);
          
          freq(a);
          //=> {1: 498, 2: 502}
          
          /*
            freqの操作は、
            元の配列aに影響を与えない
          */
          _.isEqual(a, copy);
          //=> true
          
          /*
            純粋関数を合成すると、
            純粋関数が生成される
          */
          freq(skipTake(2, a));
          //=> {1: 250, 2: 252}
          
          _.isEqual(a, copy);
          //=> true
          
          /*
            純粋性の提供に協力せずに、
            オブジェクトの内容を変更したいという
            関数もたまに存在する
          
            _.extend関数は1つ目の引数として与えられた
            オブジェクトそのものに変更を加えてしまう
          */
          var person = { fname: "Simon" };
          
          _.extend(person, { lname: "Petrikov" }, { age: 28 }, { age: 108 });
          //=> {age: 108, fname: "Simon", lname: "Petrikov"}
          
          person;
          //=> {age: 108, fname: "Simon", lname: "Petrikov"}
          
          /*
            _.extendを使ってオブジェクトを結合する
            新たな関数mergeを作成する
          
            1つ目の引数をターゲットオブジェクトとして使用する代わりに、
            空のローカルオブジェクトを挿入し、変更を加えるようにする
            このmerge関数は他の純粋関数と安全に合成できる
            
            可変性を隠蔽することにより純粋性を勝ち取ることができる
          */
          function merge(/* 任意の数のオブジェクト */) {
            return _.extend.apply(null, construct({}, arguments));
          }
          
          var person = { fname: "Simon" };
          
          merge(person, { lname: "Petrikov" }, { age: 28 }, { age: 108 });
          //=> {age: 108, fname: "Simon", lname: "Petrikov"}
          
          person;
          //=> {fname: "Simon"}
        

  • オブジェクトの不変性を観察する
    • オブジェクトのフリーズを除くと、JavaScriptのビルトインのデータ型やオブジェクトに不変性を持たせるためには、できることはほとんどない
      • JavaScriptはほんのわずかな安全して提供しない
      • 責任はすべて開発者に委ねられる
    • 自身がコントロールするJavaScriptオブジェクトだけが不変性の対象であれば、強い規律を敷くという選択肢が意味を持つようになる
    • JavaScriptの不変性の難しさ

        function Point(x, y) {
          this._x = x;
          this._y = y;
        }
        
        /*
          withXとwithYという
          2つの変更メソッドを実装する
        
          不変性を持ったオブジェクトは生成時の値を保持し、
          その値は変更されないようにする
        
          ルール
          ・不変オブジェクトは生成時の値を保持し、決して変更するべきではない
          ・不変オブジェクトに対する操作はその結果として新しいオブジェクトを返す
        */
        Point.prototype = {
          withX: function (val) {
            return new Point(val, this._y);
          },
        
          withY: function (val) {
            return new Point(this._x, val);
          },
        };
        
        var p = new Point(0, 1);
        
        p.withX(1000);
        //=> {_x: 1000, _y: 1}
        
        /*
          withXでは
          何も変更されない
        */
        p;
        //=> {_x: 0, _y: 1}
        
        /*
          2つのルールを守っても問題に突き当たることがある
        
          生成時に要素の配列を取り、（部分的な）キューに入れる
          ロジックを提供するQueueというデータ型を実装してみる
        */
        function Queue(elems) {
          this._q = elems;
        }
        
        Queue.prototype = {
          enqueue: function (thing) {
            return new Queue(cat(this._q, [thing]));
          },
        };
        
        var seed = [1, 2, 3];
        
        var q = new Queue(seed);
        
        q;
        //=> {_q: [1, 2, 3]}
        
        var q2 = q.enqueue(108);
        //=> {_q: [1, 2, 3, 108]}
        
        q;
        //=> {_q: [1, 2, 3]}
        
        seed.push(100000);
        
        q;
        //=> {_q: [1, 2, 3, 100000]}
        // q生成時に渡したseed配列を変更することによって、
        // Queueインスタンスも変更されてしまう
        // Queueインスタンスの生成時に防御的コピーを生成せず、
        // 配列の参照を直接使ってしまったことが問題
        
        var SaferQueue = function (elems) {
          this._q = _.clone(elems);
        };
        
        SaferQueue.prototype = {
          enqueue: function (thing) {
            return new SaferQueue(cat(this._q, [thing]));
          },
        };
        
        var seed = [1, 2, 3];
        var q = new SaferQueue(seed);
        
        var q2 = q.enqueue(36);
        //=> {_q: [1, 2, 3, 36]}
        
        seed.push(1000);
        
        q;
        //=> {_q: [1, 2, 3]}
        
        /*
          qインスタンスは直接アクセスして変更できる
          _qというパブリックフィールドを持っている
        */
        q._q.push(-1111);
        
        q;
        //=> {_q: [1, 2, 3, -1111]}
        
        /*
          同様にSaferQueue.prototypeメソッドも
          他の好きなメソッドに置き換えることが
          できてしまう
        */
        SaferQueue.prototype.enqueue = sqr;
        
        q2.enqueue(42);
        //=> 1764
      

  • オブジェクト操作は往々にして低レイヤー操作
    • new演算子やオブジェクトメソッドを使用することにより、突然現れる問題がある
    • オブジェクト指向と関数型の補完関係の例

        var q = SaferQueue([1, 2, 3]);
        
        q.enqueue(32);
        // TypeError: Cannot read property 'enqueue' of undefined
        // インスタンス生成時にnewを使っていないためエラーとなる
        
        /*
          決まり文句のような
          回避法がある
        */
        function queue() {
          return new SaferQueue(_.toArray(arguments));
        }
        
        var q = queue(1, 2, 3);
        
        /*
          invoker関数を使って
          enqueueを委譲する関数を生成しておく
          こともできる
        
          メソッドをそのまま呼び出す代わりに
          関数として使うことで柔軟性が手に入る
          （FPとOOPは補完関係にあるという実例）
        
          ・実際のデータ型をあまり心配する必要がなくなる
          ・ユースケースに対応した型のデータを返すことができる
          ・データ型やメソッドが変更された場合、関数を変更するだけで済むようになる
          ・事前条件や事後条件をを関数に与えることができるようになる
          ・関数合成が可能になる
        */
        var enqueue = invoker("enqueue", SaferQueue.prototype.enqueue);
        
        enqueue(q, 42);
        //=> {_q: [1, 2, 3, 42]}
      

変更コントロールのポリシー

• 変更コントロールのポリシー
  • 何らかの状態を変更することが必要なときに、副作用は必ず発生する
  • できる限り少なくするにはどうすればいいか
    • 変更の範囲をコントロールする方法は、変更するものを分離しておくこと
      • 任意のオブジェクトをその場で変更するのではなく、オブジェクトをあらかじめコンテナに格納しておいて、それを変更するようにする
    • コンテナでのアプローチ方法

        /*
          コンテナに格納して変更する方法と
          そのまま変更する方法の比較
        */
        var container = contain({ name: "Lemonjon" });
        container.set({ name: "Lemongrab" });
        
        var being = { name: "Lemonjon" };
        being.name = "Lemongrab";
        
        /*
          変数の変更は関数呼び出しの結果として
          発生するように制限も可能
        */
        var container = contain({ name: "Lemonjon" });
        container.update(merge, { name: "Lemongrab" });
        
        /*
          コンテナ型の
          シンプルな実装例
        */
        function Container(init) {
          this._value = init;
        }
        
        var aNumber = new Container(42);
        
        aNumber;
        //=> {_value: 42}
        
        Container.prototype = {
          update: function (fun /*, args */) {
            var args = _.rest(arguments);
            var oldValue = this._value;
            this._value = fun.apply(this, construct(oldValue, args));
            return this._value;
          },
        };
        
        var aNumber = new Container(42);
        
        aNumber.update(function (n) {
          return n + 1;
        });
        //=> 43
        
        aNumber;
        //=> {_value: 43}
        
        aNumber.update(
          function (n, x, y, z) {
            return n / x / y / z;
          },
          1,
          2,
          3
        );
        //=> 7.166666666666667
        
        aNumber.update(_.compose(megaCheckedSqr, always(0)));
        // Error: 0ではいけません
      

まとめ

• 本章は関数の純粋性の説明と実例から始めた
  • 内部変数を変更する必要がある場合は、それもOKということにも言及した
    • 誰も内部変数の変更に気が付かないのであれば、それは問題にはならないから
  • JavaScriptにおける不変性について説明した
    • 特定の変更パターンに注意することで、限りなく不変に近づけることができた
    • はっきりと分離されている関数は理解しやすい
      • テストも容易になる
    • これは、合成された関数についても理解しやすいということ
• 次章では、関数パイプラインという考え方を紹介する
  • 抽象と安全性を追求する

『JavaScriptで学ぶ関数型プログラミング』を読んだ 03へ続く

https://zenn.dev/shimpei_takeda/articles/e187f0b5d7c7fc