DQNで倒立振子
1. CartPole-v1を立たせる
Gymnasium(以降Gymとする)に標準搭載されているCartPole-v1を立たせる.そのために必要な要素を以下にまとめる.作成したプログラムはこちらのGithubページに公開する.
また本ページはこちらの記事を参考にさせていただいた.
以下本文
環境の準備
今回はGymが提供してくれているのでそれを導入するだけ.以下はランダム出力で倒立振子を制御するプログラム.1Episodeをリアルタイムで描画する設定.報酬は逐次書き換えられるのでトータル報酬を定義する必要がある.とは言えこれだけで簡単な描画が出来るのだから素晴らしい.
レンダーにhumanをを採用しているが学習が非常に遅くなるので要注意.
実際のコード
'''
observation:
([カートの位置,カートの速度,ポールの角度,ポールの角速度],reward, 終了条件×2,{Info})
(array([ 0.017, -0.01 , 0.002, -0.01 ], dtype=float32), {})
rewardは常に1.rewardの累計を大きくするのが目標
'''
import gymnasium as gym
import numpy as np
import time
env=gym.make('CartPole-v1',render_mode='human')
total_reward = 0
(state,_)=env.reset()
def now_policy(state):
time.sleep(0.1) # Sleep for 100ms to slow down the rendering
state = int(np.random.randint(0, 2))
if state >= 1:
action = 1
else:
action = 0
print(state)
return action
episode_over = False
while not episode_over:
action = now_policy(state)
observation, reward, terminated, truncated, info = env.step(action)
episode_over = terminated or truncated
print(observation, reward, terminated, truncated, info)
total_reward += reward
print(total_reward)
env.close()
Q-Network
Q学習たる所以であるQ値を更新するネットワーク.状態(カートの位置,カートの速度,ポールの角度,ポールの角速度)が入力データ,価値関数Q値が出力データ.ここで問題となるのがハイパーパラメータである.今回のような条件だと入力データが小さくタスクもシンプルであるため2~3層で十分である.また画像や時系列データを扱う必要がないので今回は全結合層のみで問題ない.ユニット数は64,128,256が多いので,今回は64で試す.活性化関数はとりあえずReLUで良い.これで必要な要件が決定したのでQ-Networkを実装する.
実際のコード
# Q値を出力するためのニューラルネットワーク
class N_Network(nn.Module):
def __init__(self):
super().__init__()
self.l1 = nn.Linear(parameters["input_size"], 128) # 入力4次元 → 隠れ層128ユニットへの全結合層(例:観測が4次元のとき)
self.l2 = nn.Linear(128, 128)
self.l3 = nn.Linear(128, parameters["action_size"])
# この関数を実行すれば深層学習が出来る
def forward(self, x):
x = F.relu(self.l1(x))
x = F.relu(self.l2(x))
x = self.l3(x)
return x
T-Network
Q学習の問題である不安定性を解消するためのネットワーク.Q学習では毎回正解ラベルが変わるため学習が不安定になる.そこで正解ラベルを定期的に更新する(毎回更新しない)ことで学習を安定させる.これはQ-Networkと構成が一緒なので,ループ中に更新作業を加えるだけで良いため実装なし.
経験再生(Experience Replay)
DQN(Q学習)はマルコフ決定過程に基づいている.そして時系列順にエピソードを繰り返すと現状態と1Horizon先の状態以外にも影響を受けてしまう.これはマルコフ決定過程ではないので,時系列順ではなくランダムにデータを入力する.リプレイバッファに必要な機能は以下の3つ.
1.入力データの収集
2.決められたbatch size分の入力データをランダムに取得
3.PyTorch用のTensor(テンソル)に変換
実際のコード
class ReplayBuffer:
# バッファーの定義,バッチサイズの代入
def __init__(self, buffer_size, batch_size):
self.batch_size = batch_size
self.buffer_size = buffer_size
self.buffer = deque(maxlen=buffer_size) # dequeはリストのようなもの
#関数によっては__len__()という関数が内部で知らないうちに使われる)
def __len__(self):
return len(self.buffer)
# フィードバック[カートの位置,カートの速度,ポールの角度,ポールの角速度]を取得しリプレイバッファに保存.
# 溢れたら古いデータを削除.ここでの経験は[状態,行動,報酬,次の状態]の4つ
def add(self, experience):
self.buffer.append(experience)
# バッファーからランダムにバッチサイズ分のデータを取得
def sampling(self):
datas = np.random.choice(self.buffer, self.batch_size, replace=False) # batch_size分のデータをランダムに取得
# データを分割してそれぞれの変数に格納
state = torch.tensor(np.stack([x[0] for x in datas]))
action = torch.tensor(np.array([x[1] for x in datas]).astype(np.int64))
reward = torch.tensor(np.array([x[2] for x in datas]).astype(np.float32))
next_state = torch.tensor(np.stack([x[3] for x in datas]))
done = torch.tensor(np.array([x[4] for x in datas]).astype(np.int32))
return state, action, reward, next_state, done
方策の決定
方策とは,ある状態においてどのように行動を決定するかのルールである.方策の代表例として最適方策がある.これは価値関数に基づき,現在の状態で最適だと算出される行動を常に選択する方策である.しかしこれだと1手先しか考えておらず,「その場しのぎの最善」でしかない.そこで時々ランダムな行動を混ぜることで学習のバイアスを改善する手法がある.これをε貪欲方策という.今回はこれを採用する.
実際のコード
# ε-greedyポリシーに従って行動を選択
def select_action(self, state):
if np.random.rand() <= self.epsilon:
# εの確率でランダムな行動を選択
return self.env.action_space.sample()
# 1-εの確率で最適方策に基づいて価値関数を更新
else:
state = torch.FloatTensor(state).unsqueeze(0) # PyTorchのTensorに変換+バッチ形式に対応
with torch.no_grad(): # 勾配計算を無効化
return self.q_net(state).argmax().item()
ネットワークの学習
ここが深層学習のメインといっても過言ではない.ニューラルネットワークの活用には「学習」と「出力の計算」の2つがある.
出力の計算とは,ただ入力データからネットワークを順伝搬して出力を計算することである.(N_Networkのforward関数に相当する)
一方で学習とは,損失関数をもとにニューラルネットの中にある重みを調整する過程である.DQNの場合,損失関数はTD誤差(QnetworkとTarget-networkのQ値の差)と平均二乗誤差を用いる.またこの損失関数をもとに誤差逆伝搬法によって勾配が計算し,それに基づいて重みをする.正直深層学習の詳細はなんとなくなのでまた勉強する.
この学習過程をまとめたコードを以下に示す.
実際のコード
def calc_TDerror(states, actions, next_states, rewards, dones):
# QネットワークとターゲットネットワークからQ値を取得(TD誤差を求めるため)
actions = torch.LongTensor(actions).unsqueeze(1) # [batch_size] → [batch_size, 1]
q_values = Qnet(states) # → Q(s_t, ·) 全アクションのQ値を出力(形状:[batch_size, action_dim])
# print(q_values, action)
q_value = q_values.gather(1, actions).squeeze() # actionに対応するQ値を出力(形状:[batch_size]
with torch.no_grad():
next_q_max = Tnet(next_states).max(1)[0]
q_value_target = rewards + (1 - dones) * parameters["gamma"] * next_q_max # Q値のターゲット値をベルマン方程式 に従って計算
# Q値から価値関数とTD誤差を計算.TD誤差を最小化するようにQネットワークのパラメータを更新する
loss = torch.nn.MSELoss()(q_value, q_value_target)
# 深層学習のルールに従ってQネットワークのパラメータを更新
optimizer.zero_grad() # 勾配を初期化
loss.backward() # 誤差逆伝播法で勾配を計算
optimizer.step() # Qネットワークのパラメータ(重み)を更新
コード全体
上記のコードをまとめ,ハイパーパラメータも追加したものを完成次第,Githubに公開する.(URLはページトップに記載)
また以下に学習した重みパラメータをコピーして順伝搬させることで最適方策からactionを求めた結果を以下に示す.安定していることが分かる.
学習した結果を制御に用いるには
さて,学習はこれで完了したがこのままでは本題の倒立制御が出来ていない.学習過程で倒立制御の「実験」はしてきたが,やりたいことは学習結果の「運用」である.
ということで学習結果(ネットワークの重みパラメータ)をPytorchの専用形式でファイルとして保存する.
try:
torch.save(Qnet.state_dict(), MODEL_SAVE_PATH)
print(f"モデルの重みを {MODEL_SAVE_PATH} に正常に保存しました。")
except Exception as e:
print(f"モデルの重みの保存中にエラーが発生しました: {e}")
あとはこのパラメータをQネットワークにコピーして,stateをネットワークに入力すれば最適な行動actionが出力される.このとき学習はせず順伝搬をするだけであることに注意する.
出力用のファイルも上記のGithubページに公開する.
ランダム方策の重要性について
上記にないTipsとしてε減衰というものがある.これはε貪欲方策に用いるεを,ステップが進むにつれて小さくしていく手法である.最初は探索範囲を広げるためにランダムに行動した方が効率的だが,ランダム行動が多すぎると報酬を大きくするのが難しい.一方でεが最初から最後まで小さいままだと学習のバイアスが大きくなり過学習を起こしやすくなる.そこで最初のうちの幅広く探索を行い,ある程度探索が進んだらより報酬を最大化することに注力するように設計したものがε減衰である.

図:ε減衰をしなかった場合の学習
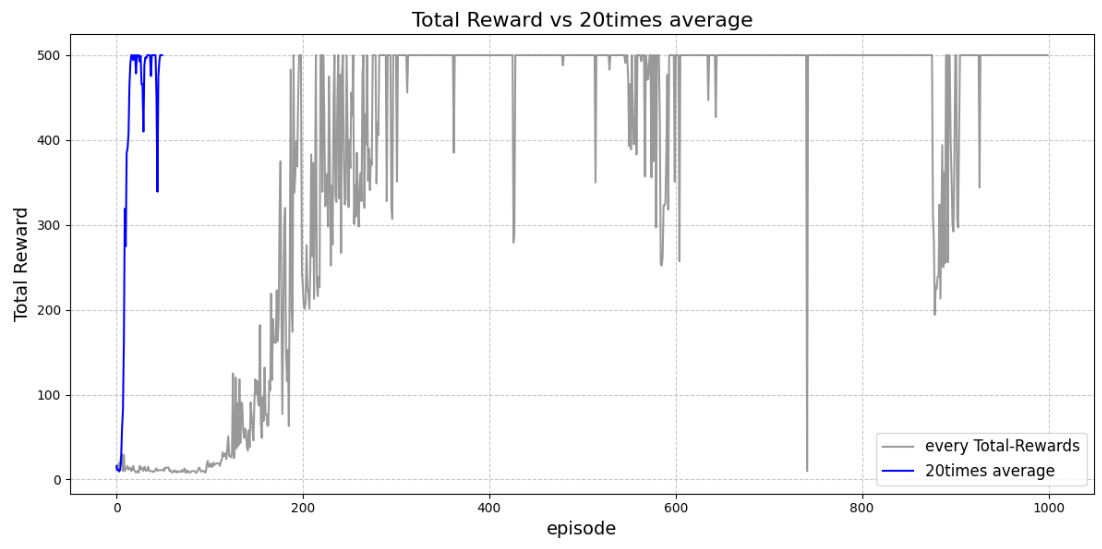
図:ε減衰をした場合の学習
2. Githubにあるロボットモデルによる倒立振子を導入する
1で出来たことをそのまま流用する.ロボットモデルとシミュレーション環境,Gym.Envの変更をする.
gym.envとwrapperの変更
やろうと思ってたけどあんま学びないかも
まずは報酬と行動空間の変更を以下のように行う.まず報酬は現在の位置と角度を考慮し,また角度の重みを大きくする.そして行動空間について右に押すか左に押すかしか決定できなかったため,これを-1から1にする.-1~0の間であれば左に,0~1の間であれば右にカートを動かすように設定する.またDQNは離散値しか計算できないので,内部的に処理を離散化する必要が生じる.
| 変数 | 変更前 | 変更後 |
|---|---|---|
| reward | 1 | -(位置×0.2 + 角度×0.8) |
| action | Discrete(2) {0, 1} | [-1, 1] |
Githubからセグウェイ型ロボットを取得しカスタム環境を構築
MujocoとGymnasiumを用いてセグウェイ型ロボットのシミュレーション環境を整える.モデルはこちらのものを採用する.
まずはMujoco環境でセグウェイ型ロボットを制御し,各種状態を取得できるようにする.
Wrapperの作成
Wrapperに必要な要素は以下のとおりである。
'''
Gym環境に必要な要素
1.観測空間の正規化: 倒立振子の位置、速度、角度、角速度を観測
2.報酬調整: 現在の位置と速度から報酬を決定
3.終了条件の調整 : 一定回数が経つor位置・角度が一定値以上になる
4.離散化(for DQN): 入力(台車の移動速度)を離散化する
5.フレームスキップ: 全てのステップを計算していると時間がかかる+実空間では処理間隔が生じるためデータ量を間引く
6.レンダリング設定
mainプログラムで呼び出すのはreset(), step(), close()のみ。それ以外はstep()に含まれる。
'''
これをもとにWrapperを作成する。以下に作成したWrapperライブラリを示す。
PIDとDQNを比較する
DQNで倒立させることが出来たのでPID制御と比較する.PID用のコードはこちらを参考にした.またこちらのページも分かり易くまとめられていた.PIDを含めた古典制御の大きな問題は1変数しか制御対象として入力できないことである.したがって今回は台車の速度と振子の回転速度の2変数を重みづけして1変数にしたものを制御対象として扱う.
また外乱に対する安定性も見たかったため,外乱を与えるコードを追加した.以下に追加した外乱用のコードを示す.
外乱制御
if np.random.rand() <= noise:
print("do")
next_state[1] += np.random.normal(0, 500) # カート速度に外乱
next_state[3] += np.random.normal(0, 500) # ポール角速度に外乱
以下に実際のシミュレーションの様子を示す.結論から言うと,PID制御でも,外乱があっても500ステップ(gym環境の最大値)倒立し続けることが出来た.また外乱を与えても,どちらの制御も安定していた.このことからもあまりPIDとDQNの性能には差が生じないことが分かる.
これ以降の文章は非常に主観かつ希望的観測なので無視して下さい
以下の内容に関する真偽には一切の責任を負いません.
このままではPID制御で十分という結論になってしまう(CartPole環境に関してはまあ,十分でした).しかし以下のような違いが深層強化学習とPID制御にはあると思いたい.
①DQNは学習の際に外乱を考慮する余地がある(まあ考慮しなくても十分安定しているのだが).
②DQNは学習の際に任意の角度や位置への制御が可能である.
そういった点ではやはり深層強化学習の方が制御のクオリティが高いといえるだろう.というかそうあって欲しい.じゃないと勉強意欲が!
(そもそもDQNはロボット制御に向いていないと思う.もともと最適解の探索を目的とした強化学習であり,出力も離散値しかとることが出来ないので,仕方がないのだが.)