LLMのCUDAカーネルを自作しよう!
本記事は、LLM・LLM活用 Advent Calendar 2025 21日目の記事です。
はじめに
pytorchは、Meta社が開発した機械学習・深層学習のためのpythonライブラリです。ユーザーは、pytorchを使用することで、画像分類モデルや強化学習モデルをはじめとし、大規模言語モデルや拡散モデルなど、多種多様なニューラルネットワークモデルを構築することが可能です。
また、pytorch内部では、CPU、TPU、GPUといった様々なプロセッサ向けに最適化された処理が実装されており、これらのプロセッサ間を容易に切り替えて使用することが可能です。例えば、大規模言語モデルの推論処理をGPU上で行いたい場合は、以下のように記述します。このようにユーザーは、入力テンソルとモデルインスタンスに対して.to("cuda")をつけるだけで、GPUを使用した処理が実行可能です。GPUを使用した処理では、CUDA関数が実行されています。
# 入力テンソルの定義
x = torch.randn([1,256],dtype=torch.float32)
# モデルの定義
model = GPT2()
""" CPUを使用した推論 """
y = model(x)
""" GPUを使用した推論 """
# xとmodelに.to("cuda")をつけるだけで、GPU上での計算が可能
x = x.to("cuda")
model = model.to("cuda")
y = model(x)
では、pytorchでGPUを使用した処理を行う際、GPU上ではどのようなCUDA関数が実行されているのでしょうか。本記事では、GPT2モデルを題材に、モデルの内部で実行されているCUDA関数を自作します。これを通して、pytorchの内部で実行されているCUDA関数に関する理解を深めます。
本記事で作成するGPT2モデルの構造は、次のとおりです。
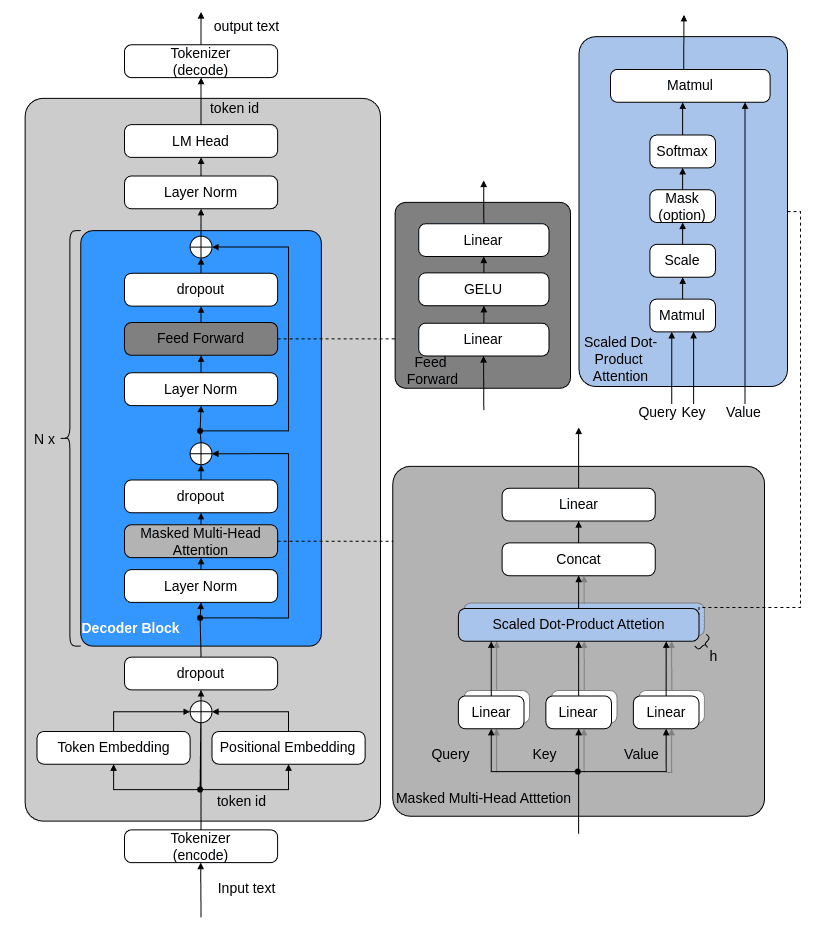
rasbt/LLMs-from-scratchを参考に、一部改変し作成
本記事では、以下の内容について記載します。
- GPT2モデルの各層のforward処理、backward処理のCUDA関数のスクラッチ実装方法
- pytorchのカスタムクラスを作成し、そこからCUDAカーネルを実行する方法
- 日本語データセットを使用した自作GPT2モデルの学習方法
関連情報
本章では、GPT2モデルのCUDA関数の自作に際して、必要な関連情報を記載します。
CUDA
CUDAは、NVIDIA GPUが処理可能なプログラム言語です。
CUDAはC++を拡張した記述方式であり、C++のcmakelistに少しの記述を追加するだけで使用可能です。
CUDAの一例は、次のとおりです。C++に似た記述形式であることがわかります。
__global__ void AddKernel(float *a, const float *b, float *c, int numElements)
{
int i = blockDim.x * blockIdx.x + threadIdx.x;
if (i < numElements) {
c[i] = a[i] + b[i];
}
}
上記のAddKernel関数はCUDAカーネル関数です。__global__修飾子が付いた関数は、CUDAカーネルと呼ばれます。
CUDAカーネルは、ホスト(CPU)側のC++コードから特別な構文で呼び出します。例えば、以下のとおりです。
torch::Tensor Add(torch::Tensor &a, torch::Tensor &b)
{
int numElements = a.numel();
a = a.contiguous();
b = b.contiguous();
float* a_ptr = (float*)a.data_ptr();
float* b_ptr = (float*)b.data_ptr();
auto options = torch::TensorOptions().dtype(torch::kFloat32).device(torch::kCUDA, 0);
torch::Tensor c = torch::empty_like(a, options);
float* c_ptr = (float*)c.data_ptr();
// Launch the Vector Add CUDA Kernel
int threadsPerBlock = 256;
int blocksPerGrid = (numElements + threadsPerBlock - 1) / threadsPerBlock;
AddKernel<<<blocksPerGrid, threadsPerBlock>>>(a_ptr, b_ptr, c_ptr, numElements);
return c;
}
CUDAライブラリ
C++におけるvector.hやiostream.h等の標準ライブラリと同様に、CUDAにも標準ライブラリが存在します。その一例は、以下のとおりです。
| ライブラリ名 | 内容 | インポート |
|---|---|---|
| cuRAND | GPUを使用した高速な乱数生成処理 | #include <curand_kernel.h> |
| cuFFT | GPUを使用した高速フーリエ変換、逆変換処理 | #include <cufft.h> |
| cuBLASLt | GPUを使用した線形代数演算処理 | <cublasLt.h> |
本記事では、これらのうち、cuRAND、cuBLASLtを使用します。
pybind
自作したCUDAカーネルは、pythonから呼び出して実行するようにします。
C++とCUDA言語のみでモデルを構築、学習、推論させることも可能です。しかし、matplotlibを使用したグラフ可視化や既にpythonで構築済みの学習スクリプトを流用するためには、自作したCUDAカーネルをpythonから実行できる方が都合が良いです。そこで、今回は、pybindを使用して、pythonからCUDAカーネルを実行できるようにします。
詳細な手順は次のとおりです。ここでは例として、前述のAddKernel関数をpythonから呼び出す方法を記載します。
まず、以下のような定義を記載したpybind_connection.cppを作成します。
#include <cuda_runtime.h>
#include <cuda_bf16.h>
#include <torch/extension.h>
#include <pybind11/pybind11.h>
#include "add.h"
py::object AddWrapper(py::handle a, py::handle b)
{
torch::Tensor a_tsr = a.cast<torch::Tensor>();
torch::Tensor b_tsr = b.cast<torch::Tensor>();
torch::Tensor out_tsr;
out_tsr = Add(a_tsr, b_tsr);
return py::cast(std::move(out_tsr));
}
PYBIND11_MODULE(add_kernel_lib, m)
{
m.doc() = "self-made torch kernel library";
m.def("add_kernel",&AddWrapper,py::arg("a"),py::arg("b"));
}
また、以下のCMakeListsを記載します。AddKernel関数の記載されたadd.cuファイルと、pybind_connection.cppを含めます。
cmake_minimum_required(VERSION 3.12)
project(add_kernel_lib)
set(CMAKE_CXX_STANDARD 17)
find_package(CUDA REQUIRED)
find_package(PythonInterp 3.10 REQUIRED)
find_package(PythonLibs 3.10 REQUIRED)
include_directories(${PYTHON_INCLUDE_DIRS})
find_package(Torch REQUIRED)
find_library(TORCH_PYTHON_LIBRARY torch_python PATH "${TORCH_INSTALL_PREFIX}/lib")
include_directories(
${PYTHON_INCLUDE_DIRS}
./pybind11/include
${CMAKE_CURRENT_SOURCE_DIR}
${CMAKE_CUDA_TOOLKIT_INCLUDE_DIRECTORIES}
)
link_directories(/usr/local/cuda/lib64)
set(CMAKE_CXX_FLAGS "${CMAKE_CXX_FLAGS} ${TORCH_CXX_FLAGS} -Wall -g")
# 基本的に、この中身を変えるだけ。
# add.cuとpybind_connection.cppを含めて、.so形式(SHARED)でビルドする
cuda_add_library(add_kernel_lib SHARED
add.cu
pybind_connection.cpp
)
target_link_libraries(add_kernel_lib
${PYTHON_LIBRARIES}
cudart
${TORCH_LIBRARIES}
${TORCH_PYTHON_LIBRARY}
)
# add_compile_definitions(INFO=1)
set_target_properties(add_kernel_lib PROPERTIES PREFIX "")
# set_property(TARGET gpu_library PROPERTY CXX_STANDARD 17)
そして、次のコマンドでadd.cuとpytorch_connection.cppをCMakeLists.txtの記述でmakeし、共有ライブラリのadd_kernel_lib.soを生成します。
source ../../.venv/bin/activate
mkdir -p build
cd build
export _GLIBCXX_USE_CXX11_ABI=1
export CMAKE_POLICY_VERSION_MINIMUM=3.5
cmake .. -DCMAKE_BUILD_TYPE=Release \
-DCMAKE_CUDA_ARCHITECTURES=89 \
-DCMAKE_PREFIX_PATH=$PWD/../libtorch \
-DCMAKE_CXX_FLAGS="-std=c++17"
make
作成した共有ライブラリはfrom add_kernel_lib import add_kernel のようにインポートすることで、ライブラリに含まれている関数をpythonから呼び出すことが可能です。
import torch
from build.add_kernel_lib import add_kernel
a = torch.Tensor([3,4]).to(torch.float32).to("cuda")
b = torch.Tensor([2,3]).to(torch.float32).to("cuda")
c = add_kernel(a,b)
print(f"a: {a}")
print(f"b: {b}")
print(f"a+b = {c}")
add_cuda関数を実行することで、次の呼び出し順序で、AddKernel関数が実行されます。
(python) add_cuda -> (pybind_Connection.cpp) AddWrapper -> (add.cu) Add -> AddKernel
Libtorch
Libtorchは、c++版のPyTorchです。こちらから最新のパッケージをダウンロードし、CMakeLists内でリンクすることで使用できます。
使用例は、以下のとおりです。python版PyTorchとほぼ同じように使用することが可能です。
#include <torch/torch.h>
#include <iostream>
using namespace std;
int main(void)
{
torch::Tensor x = torch::rand({1,256});
cout <<< x << endl;
return 0;
}
誤差逆伝播と計算グラフ
ニューラルネットワークモデルの学習では、損失関数(loss function) という評価指標を使用します。例えばその1つであるMSELoss関数は、モデルの出力値
MSELossの場合、損失関数の出力値であるlossは、値が大きいほどモデルの出力値と正解値間の差が大きいことを示しており、値が小さいほどモデルの出力値と正解値間の差が小さく、近しい値になっていることを表しています。すなわち損失関数とは、現在のニューラルネットワークが、学習データに対してどれだけ一致していないかを表す指標です。
ニューラルネットワークモデルの学習では、lossが可能な限り小さくなるように、モデルを構築する学習可能パラメータ(learnable parameters)の値を更新します。誤差逆伝播法は、ニューラルネットワークの学習手法の1つです。連鎖律を用いてlossの勾配を出力層から入力層へ逆順に計算していくことで、各学習可能パラメータのlossに対する勾配を求めます。得られた勾配は、そのパラメータの微小な変化がlossにどのような変化をもたらすかを表します。勾配が正ならパラメータを減少方向へ、勾配が負ならパラメータを増加方向へ更新することで、lossを小さくでき、モデルの出力値を正解値に近づけることができます。
連鎖律とは、「複数の関数が合成された合成関数を微分する際、その合成関数の微分は、合成関数を構成する各関数の微分の積によって与えられる」という定理のことです。例えば
連鎖律を用いることで、lossに対する各学習パラメータの勾配値を算出することが可能です。計算グラフという表現を用いて、ある学習の流れを表現したものを、下図に示します。計算グラフの○はノード、線はエッジと呼ばれます。下図の内、Wとbは学習可能パラメータです。また、Lはlossです。図のとおり、連鎖律を用いることで、Wの勾配値bの勾配値

そして、計算グラフには規則性があり、逆伝播してきた勾配に対してノードを通過した後の値をルールベースで解くことができます。例えば、加算を表す+ノード、乗算を表すxノードのルールを図に記載します。このように計算グラフを用いることで、lossに対する学習パラメータの勾配値を比較的容易に算出することができます。以降の一部のCUDAカーネルでは、計算グラフを用いることで、学習パラメータの勾配値を算出します。

なお、モデルの入力層から出力層への計算の流れは順伝播(forward propargation)、出力から入力層への連鎖律による勾配の流れは逆伝播(backward propargation)といいます。
ベースとなるCUDAカーネルを作成する
本節では、GPT2モデルを構築する上で、その基礎となるカーネルとpythonクラスを実装します。各節の名称はpythonクラス名を表しており、各節の記載内容は、forward、backward、pythonで構成されています。forwardはforward propargation時に実行される処理を、backwardはbackward propargation時に実行される処理を記載しています。
1. Linear
Linearは、入力値xにAffine線形変換を適用する関数です。
Affine変換は次のとおりです。Wはweight、bはbiasです。
weightとbiasは学習可能パラメータです。学習時には、誤差逆伝播で得られた勾配値を使用して、weightとbiasの値が更新されます。
forward
前述のAffine変換を実施します。まず、Matmul関数でxとWの内積Noneではない)場合は、biasを加算します。Matmul関数の本体であるMatmulKernelの内容は後述します。
backward
backwardの実装内容は次のとおりです。output_mask[0]=1の場合は、逆伝播してきた勾配値であるdoutとweightの内積からxの勾配値dxを算出します。output_mask[1]=1の場合は、doutとxの内積を算出し、結果の列方向の値をSumBatchwise()関数で加算し、weightの勾配値dweightを算出します。output_mask[2]=1の場合は、doutの行方向の値をSumColumnwise()関数で加算し、biasの勾配値dbiasを算出します。
学習時には、dweightの値を用いてweightを、dbiasの値を用いてdbiasを更新します。更新式には、SGDやAdamW(後述)が用いられます。
forward, backwardで必要なCUDAカーネル
前述のforward, backward処理には、Add処理に追加で、Sub、Mul、Matmul、SumColumnwise、SumRowwise関数が必要です。それぞれの本体であるCUDAカーネルについて説明します。
Sub関数の本体であるSubKernelは次のとおりです。Tensorの各要素間での差を計算します。
Mul関数の本体であるMulKernelは次のとおりです。Tensorの各要素間での積(アダマール積)を計算します。
Matmul関数の本体であるMatmulKernelは次のとおりです。aテンソルとbテンソルの内積を計算します。
SumRowwise関数の本体であるSumRowwiseKernelは次のとおりです。aテンソルを行単位で加算します。
SumColumnwise関数の本体であるSumColumnwiseKernelは次のとおりです。aテンソルを列単位で加算します。
python
pythonでのLinearクラスの実装内容は、以下のとおりです。pybindにより、linear_forwardを実行した際にはLinearForward関数が、linear_backwardを実行した際にはLinearBackward関数が実行されます。
pytorchでは、class func(torch.autograd.Function):記法を用いてforward()関数とbackward()関数を登録しておくことで、loss.backward()を実行した際に、自動的にbackward()関数が出力層から入力層へ順に呼び出され、backward propargationが実行されます。
2. GELU
GELU(Gausian Error Linear Unit)は、活性化関数の1つです。活性化関数により、モデルの中間値に非線形性を追加することができるため、より複雑な値の出力が可能となり、モデル全体の性能が向上します。
forward
arXiv:1606.08415より、GELUの計算方法は次のとおりです。
式(1)のerfは誤差関数(error function)であり、式(2)で定義されます(参考)。
Abramowitz and Stegunによると、式(2)の誤差関数は式(3)で近似できます(参考1,参考2)。
また、
式(1)(3)より、CUDAカーネルは次のとおりとなります。
backward
この時、
また、
CUDAカーネルは次のとおりです。上記の微分計算式に逆伝播してきた勾配(grad)にかけると、GELUを通過した勾配(out)が算出されます。cdfは
python
pythonでのGeluクラスの実装内容は、以下のとおりです。pybindにより、gelu_forwardを実行した際にはGeluForwardKernel(をラッピングしているGeluForward関数)が、gelu_backwardを実行した際にはGeluBackwardKernel(をラッピングしているGeluBackward関数)が実行されます。
3. dropout
dropoutは、学習時にモデルを伝播するテンソル(アクティベーション)の要素をランダムに選び、その値が閾値以下であった場合に0する操作のことを指します。これにより、過学習の抑制効果があります。推論時には、全ての要素を伝達するため、各要素の出力に対して、学習時に消去しなかった割合を乗算して出力します。
forward
まず、pythonで実装を行い、処理内容を確認します。pythonでの実装内容は、次のとおりです。
def forward(self, x, train_flg=True):
# ランダムにニューロンを消去
if self.training: # 訓練時
self.mask = np.random.rand(*x.shape) > self.dropout_ratio
return x * self.mask
else: # テスト(推論)時
return x * (1 - self.dropout_ratio)
xと同じ形状の乱数からなるテンソルを作成し、その値がdropout_ratioよりも大きい場合は1、それ以外は0にしたmaskテンソルを作成します。学習時(model.train()時)は、xテンソルにmaskテンソルをかけることで、maskテンソルが0の箇所のxテンソルを0にします。テスト時には、学習時に消去しなかった割合(1-self.dropout_ratio)を乗算して出力します。
ここで、以下のように、学習時に1/(1-self.dropout_ratio)を実施するようにします。これにより、推論時はxをそのまま返すだけでよくなるため、より効率的に推論処理が可能になります。
def forward(self, x, train_flg=True):
# ランダムにニューロンを消去
if self.training: # 訓練時
self.mask = np.random.rand(*x.shape) > self.dropout_ratio
return x * self.mask / (1 - self.dropout_ratio)
else: # テスト(推論)時
return x
この処理をCUDAで実装すると、次のとおりです。
前述のとおりcuRANDは乱数生成のためのCUDA標準ライブラリであり、cuRANDで提供されているcurand_initとcurand_uniformを用いて乱数randomを生成します(参考)。curand_initでは乱数生成器の状態を初期化し、curand_uniformで乱数を生成します。curand_initのoffsetの値を変更することで、生成された乱数列の中から使用するものを切り替えています。
生成した乱数randomがdropout_ratioの値よりも大きい場合はmask配列を1に、それ以外の場合は0にします。そして、maskが0の場合は、xを0にする処理を実施します。
backward
Backward処理は次のとおりです。逆伝播してきた勾配値に対して、順伝播の際にmaskが1であった箇所の値はそのままとし、maskが0であった箇所の値は0にします。
python
pythonでのDropoutクラスの実装内容は、以下のとおりです。pybindにより、dropout_forwardを実行した際にはDropoutForwardKernel(をラッピングしているDropoutForward関数)が、dropout_backwardを実行した際にDropoutBackwardKernel(をラッピングしているDropoutBackward関数)が実行されます。
4. Layer Norm
Layer Normですが、この記事ではDynamic Tanh(DyT)を使用します。
DyTは、2025年にKaiming Heとヤン・ルカンらが発表した、スケールされたtanh関数でLayerNorm層を置き換える手法です。pythonの場合、DyTは少ないコード(9行)で実装可能で、LayerNormやRMSNormと同等以上の性能を達成しています。また、H100環境下では、DyTはRMSNormよりも高速に動作することが確認されています。
実装が容易であるため、今回はLayerNormとしてDyTを使用します。
Forward
arXiv:2503.10622によると、forwardのpython実装は次のとおりです。
class DyT(nn.Module):
def __init__(self, num_features, alpha_init_value=0.5):
super().__init__()
self.alpha = nn.Parameter(torch.ones(1) * alpha_init_value)
self.weight = nn.Parameter(torch.ones(num_features))
self.bias = nn.Parameter(torch.zeros(num_features))
def forward(self, x):
x = torch.tanh(self.alpha * x)
return x * self.weight + self.bias
CUDAコードは次のとおりです。CUDAでは、追加のヘッダファイルなしでtanf()関数やcosf()関数などの三角関数処理が使用可能です。
backward
計算グラフを使用して、backward処理の流れと、x、

これをCUDAカーネルとして実装すると、次のとおりです。
python
pythonでのDyTクラスの実装内容は、以下のとおりです。pybindにより、dyt_forwardを実行した際にはDytForwardKernel(をラッピングしているDytForward関数)が、gelu_backwardを実行した際にはDytBackwardKernel(をラッピングしているDytBackward関数)が実行されます。
5. embedding
embeddingは、単体のトークンIDをベクトル表現に変換する処理を行います。
forward
まず、forward処理について説明します。embeddingは、トークンIDの番号に対応するベクトルを、weightテンソルから抜き出して返します。この処理は、pythonで実装すると次のとおりです。
import torch
# weight: embedding table (vocab_size=5, hidden_size=3)
weight = torch.tensor([
[1,2,3],
[4,5,6],
[7,8,9],
[10,11,12],
[13,14,15]
])
# indices: 選択するインデックス
indices = torch.tensor([1, 3, 0])
# embedding処理の実態
selected_rows = weight.index_select(0, indices)
print(selected_rows)
"""
# 出力結果
tensor([[ 4, 5, 6],
[10, 11, 12],
[ 1, 2, 3]])
"""
GPT2モデル上では、indicesは入力トークンID列です。weightの各行番号に対して、入力トークンで選択したindexと一致する行ベクトルを返す処理が、embeddingの処理です。
これをCUDAで実装すると、次のようになります。
backward
次に、backward処理を実装します。
padding_idxの値のidxは、学習対象から除外されます。学習可能パラメータを学習対象から除外するためは、その勾配値を0に設定します。例えばSGDのように、学習時の重み更新は
backward処理のCUDAカーネルは次のとおりです。
逆伝播してきた勾配(grad)の各行の値を、forward時のindeceisの各要素が指し示す重みの勾配値(out)の行番号に加算するだけです。
同じタイミングで同じVRAM領域に書き込むと競合が発生し、うまく反映されない場合があります。競合を防ぐため、gradの行単位ではなく列単位で別thread(i)を割り当て、それぞれで計算させます。
python
pythonでのEmbeddingクラスの実装内容は、以下のとおりです。pybindにより、embedding_forwardを実行した際にはEmeddingForwardKernel(をラッピングしているEmbeddingForward関数)が、embedding_backwardを実行した際にはEmbeddingBackwardKernel(をラッピングしているEmbeddingBackward関数)が実行されます。
7. Scaled Dot Product Attention
Scaled Dot Product AttentionはSelf-Attentionとも呼ばれ、query、
key、およびvalueテンソルに対して、スケールされたドット積アテンションを計算します。
forward
Scaled Dot Product Attentionをpythonで実装すると、次のとおりです。
def scaled_dot_product_attention(query, key, value, mask=None):
dim_k = key.size(-1)
scores = (query@key.transpose(-2,-1))
scores /= (dim_k**0.5)
if mask is not None:
scores = scores.masked_fill(mask==0,float("-inf"))
weights = F.softmax(scores, dim=-1)
out = weights @ value
return out,weights
この処理をCUDAカーネルを用いて実装すると、次のとおりです。
DivideSqrtKsize関数は、wの各要素をsqrt(k.size(-1))で割る処理です。関数内で使用されているCUDAカーネルは、次のとおりです。
MaskedFill関数は、wの各要素をmask_castの各要素を比較し、mask_castが0の要素は-infに置き換える処理です。関数内で使用されているCUDAカーネルは、次のとおりです。
SoftmaxForward関数は、次式で表されるSoftmax計算を実施しています。
CUDAカーネルの実装内容は、次のとおりです。
backward
計算グラフを使用して、backward処理の流れと、
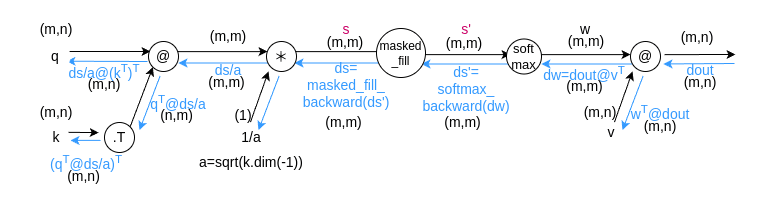
この図を元に、Backward関数を実装します。実装内容は次のとおりです。
SoftmaxBackward関数は、Softmax関数のBackwardに対応する処理を実施しています。
まず、pythonでその実装内容を記載します。sftには、Softmax関数の計算結果(SoftmaxForwardKernelの結果)が入っています。
def softmax_backward_4d(sft,grad_out):
identity = torch.eye(sft.size(-1)).view(-1,sft.size(-1)**2)
identity = torch.cat([identity for i in range(int(sft.numel()/sft.size(-1)))], dim=0)
identity = identity.view(sft.size(0),sft.size(1),sft.size(2),-1)
d_sft = sft.unsqueeze(-2)
d_sft = d_sft.expand(-1,-1,-1,sft.size(3),-1)
d_sft = d_sft.reshape(sft.size(0),sft.size(1),sft.size(2),-1)
sft = sft.unsqueeze(-2)
d_sft = \
d_sft * identity - (sft.transpose(-1,-2) @ sft).view(sft.size(0),sft.size(1),sft.size(2),-1)
grad_out = grad_out.unsqueeze(-2)
grad_out = \
grad_out @ d_sft.view(d_sft.size(0),d_sft.size(1),d_sft.size(2),grad_out.size(-1),-1)
return grad_out.squeeze(-2)
CUDAカーネルでの実装内容は、次のとおりです。
python
pythonでのScaledDotProductAttentionクラスの実装内容は、以下のとおりです。pybindにより、sdpa_forwardを実行した際にはSdpaForwardKernel(をラッピングしているSdpaForward関数)が、sdpa_backwardを実行した際にはSdpaBackward関数が実行されます
GPT2モデルを構築する
本章では、前章で作成したベースカーネルを用いて、GPT2を構成する各層を実装します。そして、それらを1つにまとめ、GPT2モデルを実装します。
1. Feed Forward層
FeedForward層の構造は、下図のとおりです。
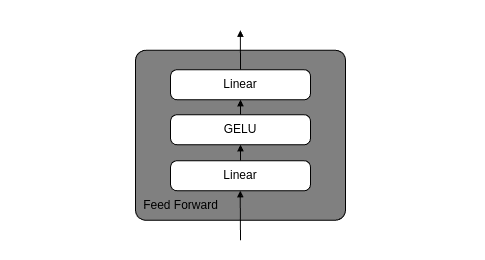
FeedForward層は、前章で作成したpythonクラスを用いて、次のように記載できます。
2. Masked Multi-Head Attention層
Masked Multi-Head Attention層の構造は、下図のとおりです。
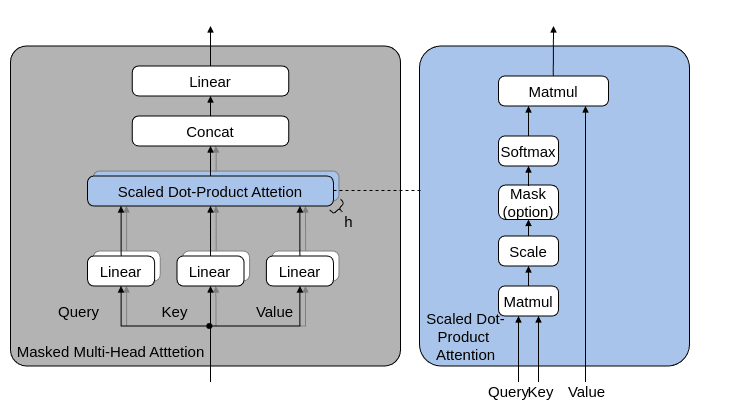
pythonでの実装内容は、次のとおりです。
3. Decoder Block層
Decoder Block層の構造は、下図のとおりです。
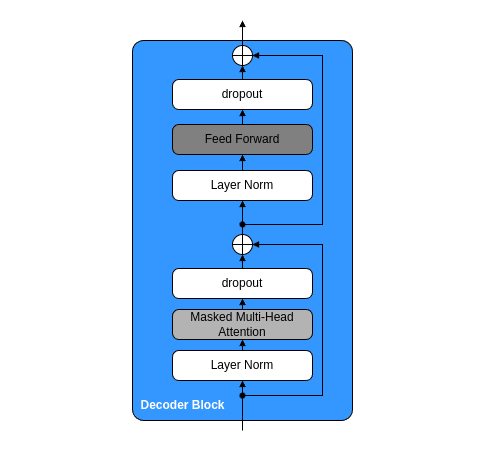
Decoder Block層は、作成したpythonクラスを用いて、次のように記載できます。
ここで、spy関数とfork関数とadd関数という自作関数を使用しています。
spy関数は、次のとおりです。これはデバッグ用の関数で、backward propargation時に伝播してきた勾配値を取得(spy)するために使用しています。
fork関数は、次のとおりです。計算グラフの「分岐ノード」を作成する関数です。forwardでは、入力テンソルxを、2つに複製しています。backwardでは、逆伝播してきた2つの勾配を加算して1つにしています。
add関数は、次のとおりです。2つのテンソルを加算するための関数です。add_forward関数からは、前述のAddKernel関数が実行されています。
4. LM Head層
LM Headは、単なるLinearです。pythonでの実装内容は次のとおりです。
5. Embedding層
Embedding層の構造は、下図のとおりです
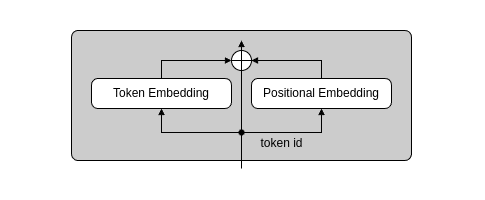
pythonでの実装内容は、次のとおりです。
ここで、batch_expandという自作関数を使用しています。これは、テンソルxのバッチ次元(0)のサイズを拡張するための関数です。
6. GPT2モデル
これまでに実装したEmbedding層、Decoder Block層、LM Head層と、Layer NormとDropoutを組み合わせ、GPT2モデルを構築します。GPT2モデルの構造は、下図のとおりです。
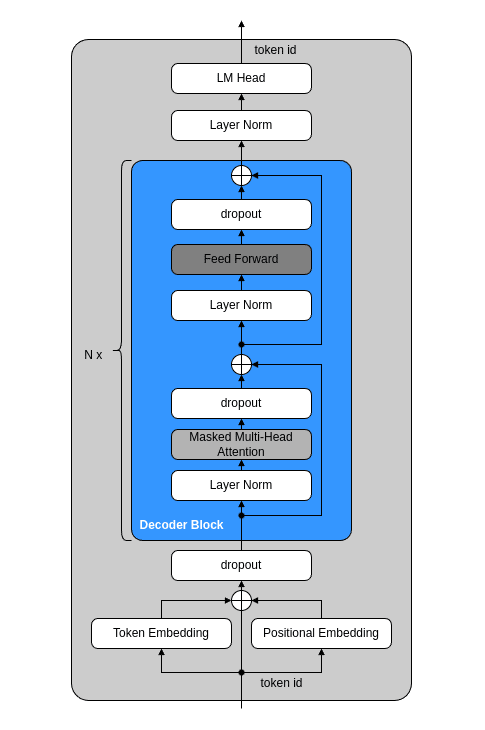
pythonでの実装内容は次のとおりです。
学習に必要なCUDAカーネルを作成する
1. CrossEntropyLoss
CrossEntropyLossは、予測値と正解値間のlossを算出するための関数の1つです。学習時には、このlossを減少させるように、モデル内の学習可能パラメータの値を更新します。
pytorchの実装では、CrossEntropyLossの計算式は、次式のとおりです。pytorch実装のdefault設定であるreduction==mean時の数式を表しています。
この時、添字のnはデータのインデックス数を表しており、Cは次元数を表しています。
forward
少々わかりにくいので、python実装したプログラムAを記載します。
import torch.nn.functional as F
import torch
import torch.nn as nn
batch_size = 4
num_classes = 3
torch.manual_seed(42)
predictions = torch.randn(batch_size, num_classes)
print("Predictions:\n", predictions)
# Predictions:
# tensor([[ 0.3367, 0.1288, 0.2345],
# [ 0.2303, -1.1229, -0.1863],
# [ 2.2082, -0.6380, 0.4617],
# [ 0.2674, 0.5349, 0.8094]])
targets = torch.randint(0, num_classes, (batch_size,))
print("Targets:\n", targets)
# Targets:
# tensor([2, 1, 2, 0])
"""公式実装の確認"""
loss = F.cross_entropy(predictions, targets)
print("Cross-entropy loss:", loss.item())
# Cross-entropy loss: 1.6134321689605713
"""cross entropyの自作"""
log_probs = torch.log(torch.softmax(predictions, dim=1))
print("Log probs:\n", log_probs)
# Log probs:
# tensor([[-0.9988, -1.2067, -1.1011],
# [-0.6511, -2.0043, -1.0678],
# [-0.2090, -3.0552, -1.9555],
# [-1.3928, -1.1253, -0.8508]])
batch_size = predictions.size(0)
probabilities = torch.zeros(batch_size, device=predictions.device)
for i in range(batch_size):
# log_probsの[i行目,"targets[i]"列]目の値を抽出
probabilities[i] = log_probs[i, targets[i]]
print("Probabilities:", probabilities)
# Probabilities: tensor([-1.1011, -2.0043, -1.9555, -1.3928])
loss = -probabilities.mean()
print("Cross-entropy loss:", loss.item())
# Cross-entropy loss: 1.6134321689605713
なお、CrossEntropyLossには、ignore_indexという引数があります。これは、この値と同じ値をもつ正解データのインデックスは、lossの計算対象から除外するという設定値です。これは、例えば意図的に学習対象から除外したいデータがある場合に使用されます。以下は、ignore_idx=-1に設定した場合のpython実装です。
import torch.nn.functional as F
import torch
import torch.nn as nn
batch_size = 4
num_classes = 3
ignore_index = -1
torch.manual_seed(42)
predictions = torch.randn(batch_size, num_classes)
print("Predictions:\n", predictions)
# Predictions:
# tensor([[ 0.3367, 0.1288, 0.2345],
# [ 0.2303, -1.1229, -0.1863],
# [ 2.2082, -0.6380, 0.4617],
# [ 0.2674, 0.5349, 0.8094]])
targets = torch.randint(0, num_classes, (batch_size,))
targets[3] = -1
print("Targets:\n", targets)
# Targets:
# tensor([2, 1, 2, -1])
"""公式実装の出力確認"""
loss = F.cross_entropy(predictions, targets, ignore_index=ignore_index)
print("Cross-entropy loss:", loss.item())
"""cross entropyの自作"""
log_probs = torch.log(torch.softmax(predictions, dim=1))
print("Log probs:\n", log_probs)
# Log probs:
# tensor([[-0.9988, -1.2067, -1.1011],
# [-0.6511, -2.0043, -1.0678],
# [-0.2090, -3.0552, -1.9555],
# [-1.3928, -1.1253, -0.8508]])
batch_size = predictions.size(0)
probabilities = torch.zeros(batch_size, device=predictions.device)
ignore_cnt = 0
for i in range(batch_size):
# log_probsの[i行目,"targets[i]"列]目の値を抽出
if targets[i] == ignore_index:
ignore_cnt+=1
continue
probabilities[i] = log_probs[i, targets[i]]
print("Probabilities:", probabilities)
# Probabilities: tensor([-1.1011, -2.0043, -1.9555, -1.3928])
loss = -1*probabilities.sum()/(probabilities.size(-1)-ignore_cnt)
print("Cross-entropy loss:", loss.item())
これらの情報をもとに、CrossEntropyLossをcudaカーネルとして実装します。
backward
backwardをpythonで実装すると、次のようになります。
import torch.nn.functional as F
import torch
import torch.nn as nn
batch_size = 5
num_classes = 3
torch.manual_seed(42)
x = torch.randn(batch_size,num_classes).requires_grad_(True)
torch.Tensor.retain_grad(x)
print("x:\n",x)
# x:
# tensor([[ 0.3367, 0.1288, 0.2345],
# [ 0.2303, -1.1229, -0.1863],
# [ 2.2082, -0.6380, 0.4617],
# [ 0.2674, 0.5349, 0.8094]])
targets = torch.randint(0, num_classes, (batch_size,))
print("Targets:\n", targets)
# Targets:
# tensor([2, 1, 2, 0])
loss = F.cross_entropy(x, targets)
print("Cross-entropy loss:", loss.item())
loss.backward()
print("x.grad",x.grad)
""" scratch """
# softmax
ex = torch.exp(x)
s = torch.sum(ex,dim=-1)
print("ex:\n",ex)
print("s:\n",s)
s = s.view(1,-1).T.expand(-1,num_classes)
print("s:\n",s)
y = ex/s
print("y:\n",y)
for i in range(batch_size):
y[i, targets[i]] -= 1
z = y/batch_size
print("z",z)
print(torch.allclose(x.grad,z,atol=1e-5))
これをCUDAカーネルで実装すると、次のとおりです。xは、CrossEntropyLossForwardで既にexp(x)化したものを使用します。
python
pythonでのCrossEntropyLoss関数の実装内容は、以下のとおりです。pybindにより、cross_entropy_loss_forwardを実行した際にはCrossEntropyLossForwardKernel(をラッピングしているCrossEntropyLossForward関数)が、CrossEntropyLossBackwardKernel(をラッピングしているCrossEntropyLossBackward関数)が実行されます。
最下部のcross_entropy()を使用することで、CrossEntropyLoss計算が可能です。
2. AdamW
AdamWは、ニューラルネットワークモデル内に含まれる学習可能パラメータを更新するための、最適化関数の1つです。AdamWの計算式は、次のとおりです(参考)。学習可能パラメータは
【AdamW】
input :
initialize :
for
return
これをCUDAカーネルで実装すると、次のとおりです。paramは学習可能パラメータdparamは勾配値mはvはparamは
pythonからは、次のように呼び出して使用します。adamw_forwardを実行することで、AdamWKernel(のラッパー関数であるAdamW)が実行されます。param.data, self.state[i]["m"], self.state[i]["v"] = adamw_forwardの部分でadamw_forwardから返り値としてself.state[i]["m"]とself.state[i]["v"]に保存しておくことで、次回パラメータ更新時に
自作関数の出力をテストする
自作したCUDAカーネル、およびそれを実行するpythonクラスのforward()、backward()の出力が正しいかどうかは、pytorchでの同機能関数におけるforward()、backward()の実行結果と一致するかで否かで判断しています。
例えば、自作のLinearクラスは、pytorchのnn.Linearクラスとの比較検証をしています。テストプログラムは、次のとおりです。pythonのunittestライブラリを使用し、テストコードを作成しています。
この他にも、今後説明する複数の自作pythonクラスにおいて、pytorchとの比較を行っています。それらはすべて、公開リポジトリのtests/pythonフォルダに入っており、次のコマンドを実行することで一括実行が可能です。
# コードはunittestだが、pytestコマンドで実行ができ、出力がきれいに表示される
uv run pytest ./tests/python -v
# pytestでlog-levelを渡してやることで、python loggerモジュールの出力制御ができる
uv run pytest -log-cli-level=INFO ./tests/python -v
テスト実行時の出力例は、以下のとおりです。39個のテスト関数すべてをpassしていることがわかります。
========================================== test session starts ==========================================
platform linux -- Python 3.10.12, pytest-8.3.5, pluggy-1.5.0 -- /workspace/diy-torch-kernel/.venv/bin/python
cachedir: .pytest_cache
rootdir: /workspace/diy-torch-kernel
configfile: pyproject.toml
collected 39 items
tests/python/test_activation.py::TestGelu::test_backward PASSED [ 2%]
tests/python/test_activation.py::TestGelu::test_forward PASSED [ 5%]
tests/python/test_embedding.py::TestEmbedding::test_backward PASSED [ 7%]
tests/python/test_embedding.py::TestEmbedding::test_backward2 PASSED [ 10%]
/* omit */
tests/python/test_optim.py::TestAdamW::test_forward PASSED [ 94%]
tests/python/test_optim.py::TestSGD::test_forward PASSED [ 97%]
tests/python/test_optim.py::TestSGD::test_forward_momentum PASSED [100%]
===================================== 39 passed in 83.22s (0:01:23) =====================================
学習
これまで作成したCUDAカーネルを使用し、 GPT2モデルの学習を行います。
データセット
データセットは、以下の0.9Bのものを使用します。
こちらのスクリプトを使用し、ダウンロードします。
後述の学習スクリプト内で、データセットを学習データ:テストデータ=9:1に分割して使用します。
モデルサイズ
学習時間を削減するために、モデルサイズは36Mとします。
構成としては、rinna/japanese-gpt2-xsmallとほぼ同じです。
トークナイザー
トークナイザーは、Sentencepieceを使用して作成します。
トークナイザーの学習は、以下のスクリプトで実施します。学習データセットは、前述のce-lery/wikiデータセットを使用します。
学習スクリプト
学習スクリプトは、以下のとおりです。
LLMs-from-scratchをベースに作成しています。
学習結果
学習時のlossの推移は、下図のとおりです。

最終的なtrain, eval lossの値と、学習時間は以下のとおりです。
Ep 1 (Step 305000): Train loss 4.330, Val loss 4.325
[66:40:45<00:00, 1.27it/s]
なお、pytorchで同様のモデルを学習させた際のlossの推移は、ほぼ同じでした。
終わりに
本記事では、GPT2モデルの内部で実行されているCUDAカーネルを自作しました。また、自作したCUDAカーネルをpythonから呼び出し、モデルの学習を実施しました。学習時間とメモリ消費量はpytorchには劣るものの、lossは同様に推移する結果が得られました。
今回は学習結果として、lossの推移しか示せませんでした。pytorchで学習した際のlossの推移や、自作モデルの推論結果は、今後このページに追加予定です。
また、学習時間の向上と、メモリ消費量の削減のため、CUDAカーネルと周辺プログラムの改善を実施します。
Discussion