🙆
計算機を使って常微分方程式の問題を解く
ここでは常微分方程式の練習問題を計算機を使って解く方法を纏める。
全ての問題ではなく特徴的な問題だけを解く。
計算機
今回はMathDFとSymPyを使う。詳しくはこちらに。https://zenn.dev/ryoooou/articles/c826659b115666
MathDF
SymPy
以下のコードを使う。
違い
- MathDF
途中式が得られる
利用が容易
限られた解法でしか解けない - SymPy
途中式は得られない
少し勉強が必要
複数の解法を比較できる
練習問題
変数分離形微分方程式[1]

MathDF
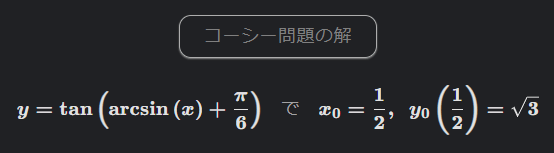
SymPy
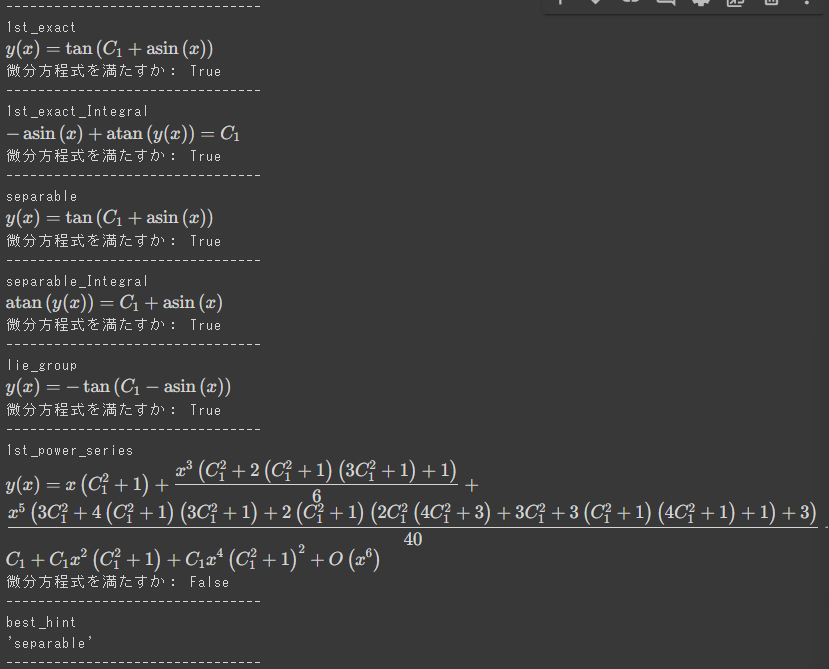
このように複数の解法の結果が求められ、separable(変数分離形)がbest_hint(最適な解法)だと示される。
separableで初期条件下で微分方程式を解くと、模範解答と同じ次の特殊解が得れれる。

同次形微分方程式[2]

MathDF

SymPy


1st_homogeneous_coeff_best(1次同次方程式?)が最適な解法だと示される。模範解答と等しい。
線形微分方程式[3]

MathDF

SymPy
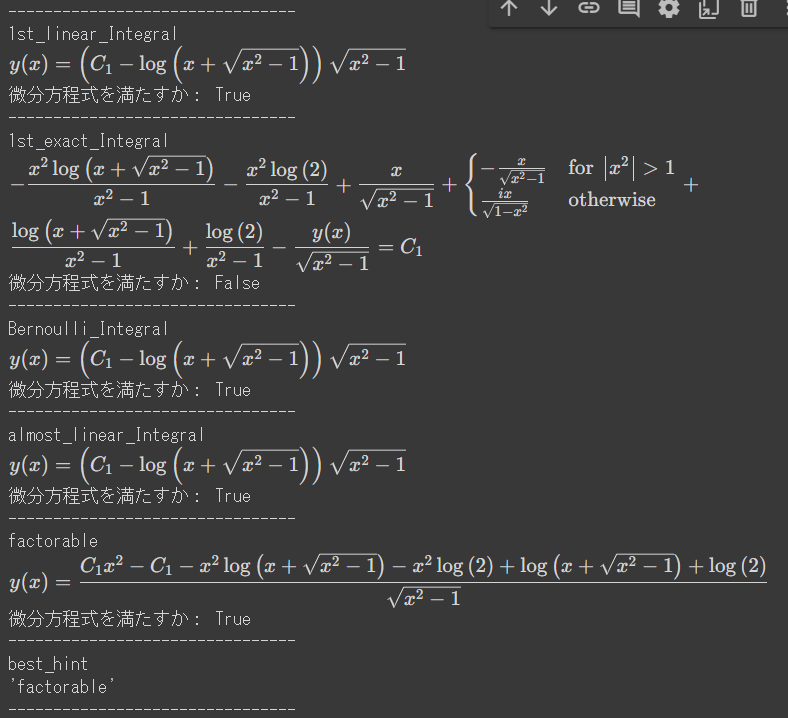
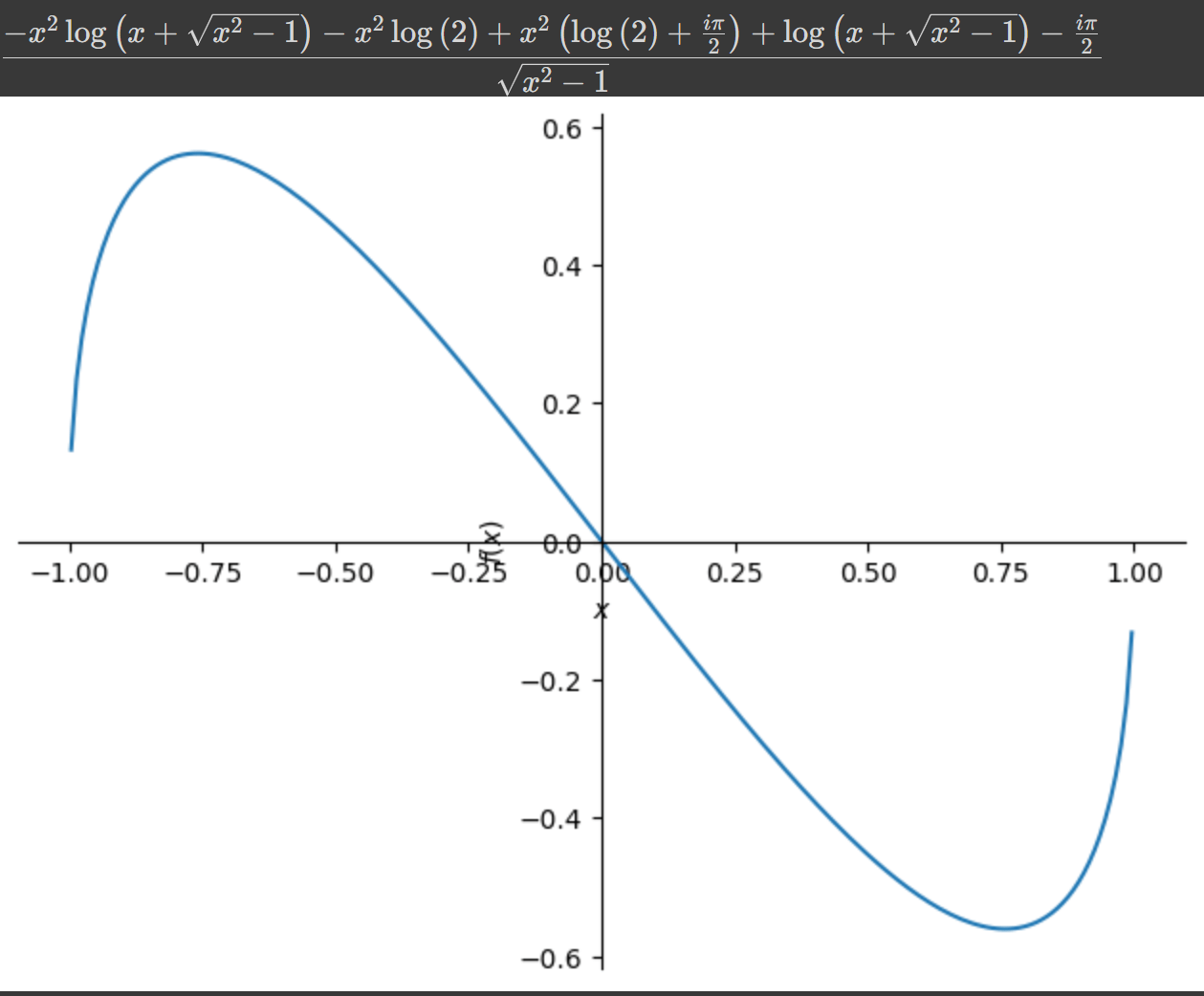
factorableは模範解答とは違うが、定数C1を複素数まで含めると-1<x<1の範囲の特殊解も得られる。
例えば、初期値f(0)=0で解くと、
また、almost_linear_Integralの式を変形するとまさに-1<x<1の範囲の模範解答となる。
つまり、計算機で求めた一般解の方がxの定義域全体を1つの関数でカバーする事から、模範解答より望ましいと考えることが出来る。[4]
ベルヌーイの微分方程式[5]
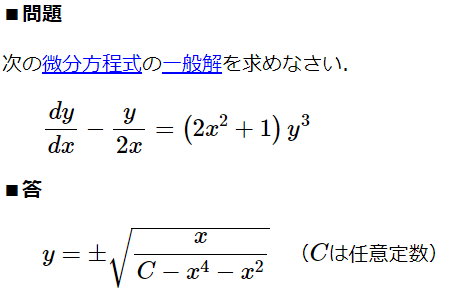
MathDF

SymPy

完全微分方程式[6]

MathDF

SymPy

factorableがbest_hintだが初期条件を満たす特殊解はない事が分かる。
そのため1st_exact_Integralに切り替えて初期条件下で微分方程式を解くと特殊解が求まる。
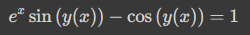
2階線形微分方程式[7]

MathDF
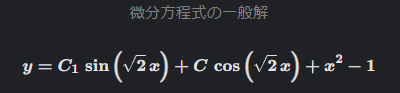
SymPy

連立微分方程式[8]
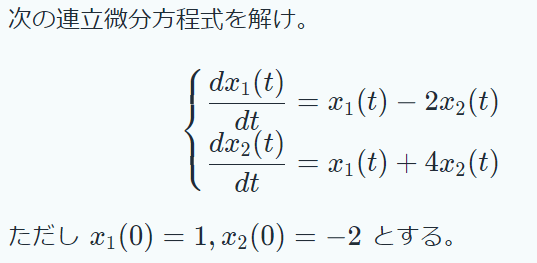
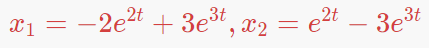
MathDF
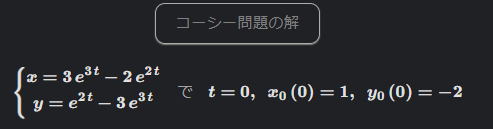
SymPy
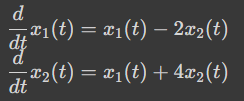
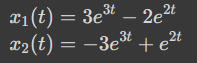
Discussion