数式処理システムの全体像
数式処理システム[1]の全体像を端的に纏めてみる。
数式処理システム
computer algebra system (CAS)ともいう。
つまり、手計算と同じように代数学の要領でコンピュータで数式を操作し厳密解を求めるシステムである。これを記号計算という。[2]
反対に数値としてコンピュータで計算することを数値計算という。[3]数値計算ではコンピュータの扱える桁数が有限であることから誤差が問題となる。
主な数式処理システム
有償
どちらとも高価。(年数十万円)
Mathematicaの方がMapleより2倍ほど高い。Mathematicaの方が比較的高性能でサポートも充実しているようだが、優劣は個人の好みによるみたいである。[6]
これらは数式処理システムだけでなく、数値計算や可視化、最適化などの機能も含まれるソフトウェアシステムである。
無償
- SageMath[7]
無償のソフトウェアを統合して有償に近いソフトウェアシステムを実現したもの。数式処理システム以外も含まれる。
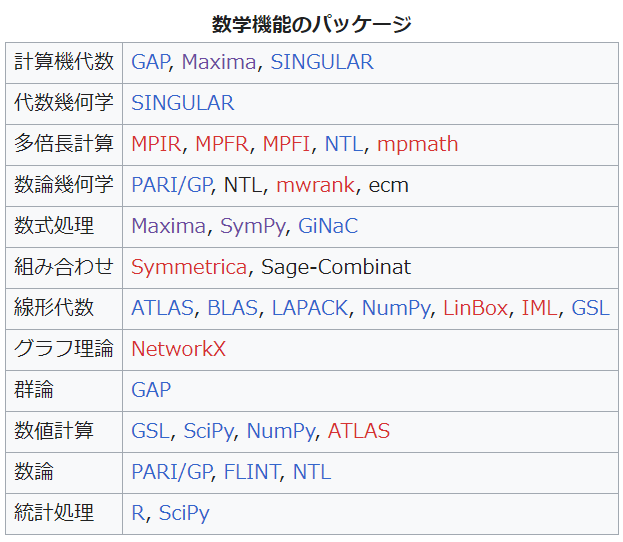
SageMathに含まれる主な無償の数式処理システム
- SymPy[8]
Pythonで書かれたシンプルで軽量な数式処理システム。最小限の構成になっている。 - Maxima[9]
LISPで書かれたSymPyより重量な数式処理システム。数式処理システム以外の可視化ツールなども含まれる。
比較
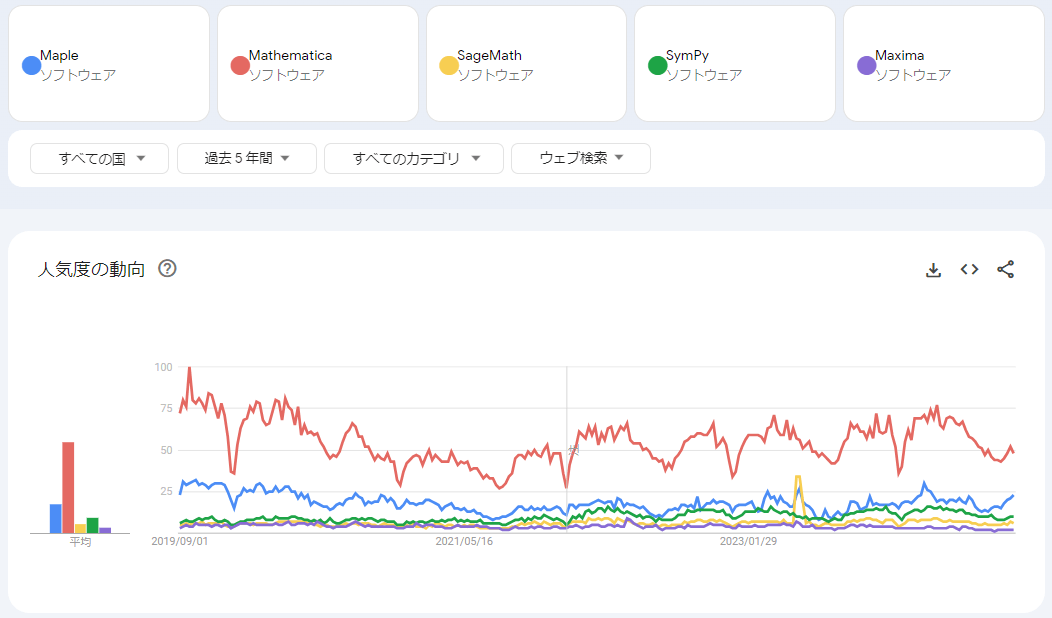
知名度は有償ではMathematicaが優勢、無償ではSymPyが優勢。
性能はMathematica>Maple>SageMath>Maxima>SymPyの順。
学びやすさはSymPy>Maple=Mathematica>SageMath>Maximaの順。
有償なら財布の紐が許せばMathematicaだが、Mapleでも十分。
無償なら大規模で複雑な数式処理にはSageMath、簡単なものにはSymPyが最適。
試す方法
SageMath
以下の記事を参考に環境を構築し、文法の勉強をすればオンライン上で試せる。
SymPy
こちらは環境構築は要らず、文法の勉強をすればオンライン上で試せる。
もっと手軽に使える数式処理システム
他にもGUIベースの数式処理システムも幾つかある。
このようなシステムには途中式の表示のような、CUIベースのシステムではできないことが可能なものもある。しかし柔軟性は低い。
ほとんどのシステムでは途中式の表示は有料だが、mathdfでは無料で使える。
Discussion