統計検定準1級 ワークブック 補助資料集
統計検定準1級対応のワークブックは網羅性は高いですが、分かりにくい部分が多いので、色々なサイトでそれを補完する必要があるのですが、それを纏めたサイトは少ないです。
なので、協力して高品質な補助資料集を作れる場を、zennのgithub連携を利用して作ってみました。
是非、参考になったURLや説明、練習問題などを追加してみてください。
協力方法
まず、githubアカウントを持ってない方はアカウントを作成して、
次に下のページにアクセスして、
ペンボタン(Fork this repository and edit the file)をクリック
そうしたら編集画面が出てくるので、ここで変更。
変更が終わったら、Commit changes... ボタンを押して、Extended descriptionに何を変更したかを書いたら(明白な場合はなくてもいいです)、Propose Changesをクリックして完了。
可能な限り早く対応します。
参考になる準1級全体の記事
出題傾向をまとめたサイト。勉強の配分に非常に役に立つので、章の後ろに出題頻度を付け加えました。
編集方針
が素晴らしいので、基本的にこれをベースに他のサイトで補完していく形にします。
暗記帳
Ankilotの共同編集を使って暗記帳を作る。安定動作が100枚以下なので、8章ごとで分けました。
共同編集のパスワードは1。
1.事象と確率 5/6
2.確率分布と母関数 0/6
3.分布と特性値 5/6
色々な平均
偏相関係数
4.変数変換 0/6
5.離散型分布 5/6
6.連続型分布と標本分布 6/6
頻出の指数分布
2変量、多変量正規分布
7.極限定理、漸近理論 0/6
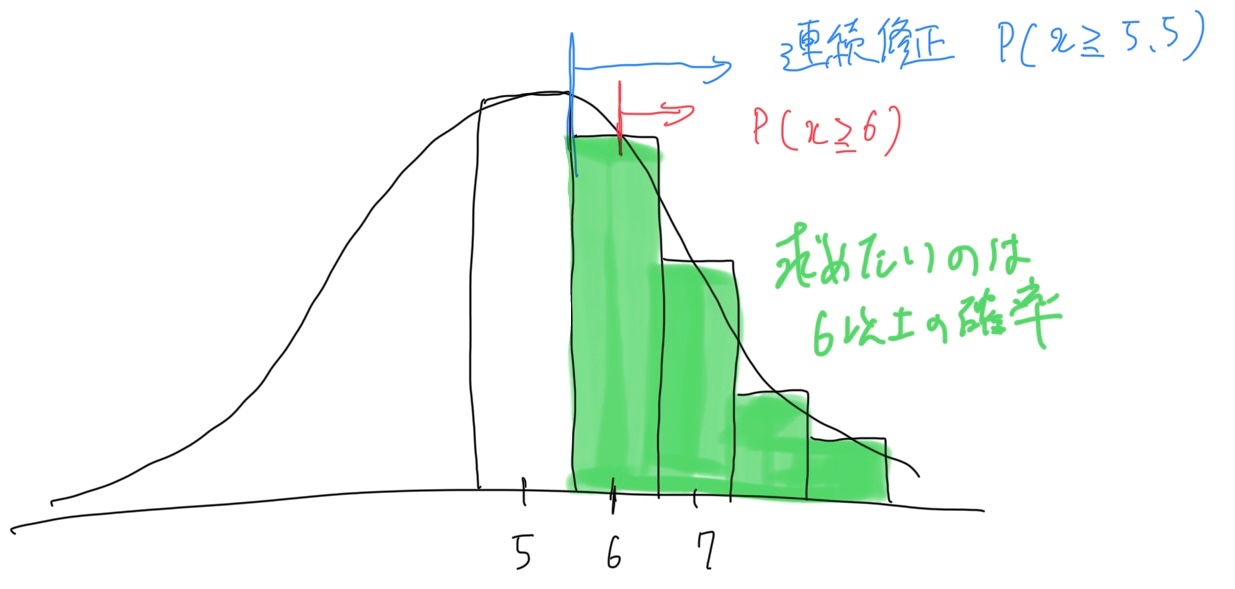
連続修正は図のように棒の中心ではなく端から合計するイメージ。
デルタ法:
8.統計的推定の基礎 1/6
この章は難しくて重要なイメージ。
これまで何となく使ってきた用語をしっかりと意味を理解する。
- 母数(パラメータ):母集団の特徴を表す母平均,母分散などの神のみぞ知る値。パラメータという命名が非常に分かりづらいので、パラメータ=母数であることに気を付けて読み進めましょう。
私たちは標本の情報から母数をどうにかして推定すること(統計的推定)で、母集団の特徴を知ろうとする訳ですね。
-
推定量:標本から母数を推定するアルゴリズム(関数)またはそれによって求められる値。例えば母平均の推定量には標本平均があり、母分散の推定量には標本分散があります。
-
統計量:母数の情報を含まない、標本の情報のみを利用したアルゴリズム(関数)またはそれによって求められる値。例えば母平均は含まないが、標本平均は含む。
推定量と統計量は曖昧なので分かりにくい。統計量+母数を推定するために使う=推定量と考えれば十分。実際、標本平均は統計量、推定量どちらでも使える。
このようにこの章では、簡単そうな名前でありながら厄介な用語があるので、よく意識しながら進めた方がいいと思います。
-
尤度関数(likelihood function):これも本来の定義としては曖昧なのですが、この章では、仮の母数を入力したら、その仮の母数が真の母数である尤もらしさを出力する関数L(θ)として、使われている。
-
最尤推定量:尤度関数を最大化する母数。最尤推定量は唯一ではないこともあるし、存在しないことさえある。
-
最尤法:尤度関数の最大となる母数を真の母数と推定する方法。例えば、母平均を求めたい時は、得られた標本が仮定した母平均(θ)により生成された確率
f(X_{1};θ)
https://youtu.be/6XQJIQw-tUk?si=oWzGJKHQY5ONuNgS
-
順序統計量:標本を昇順に並べた統計量。1番目の順序統計量
X_{(1)} X_{(n)}
https://www.eeso.ges.kyoto-u.ac.jp/emm/materials/basic_stat/orderstat -
モーメント:モーメント法を学ぶためにモーメントの理解が必要。a周りのn次のモーメントは
E[(X-a)^n] \mu_{n} \mu'_{n}
https://www.hello-statisticians.com/explain-terms-cat/moment1.html -
モーメント法:モーメントの連立方程式で、推定量を得る方法。
https://youtu.be/uoTmUlMDiq0?si=HAYG79PJRMBCv0VU -
不偏性:その推定量が平均的に過大にも過小にも母数を推定しておらず、推定量の期待値が母数に等しいことを意味する。
https://bellcurve.jp/statistics/course/8612.html -
バイアス:母集団から抽出した標本の分布が、母集団の分布と比べて偶然ではないずれを起こしているとき、バイアスがあると言う。
https://bellcurve.jp/statistics/glossary/1382.html
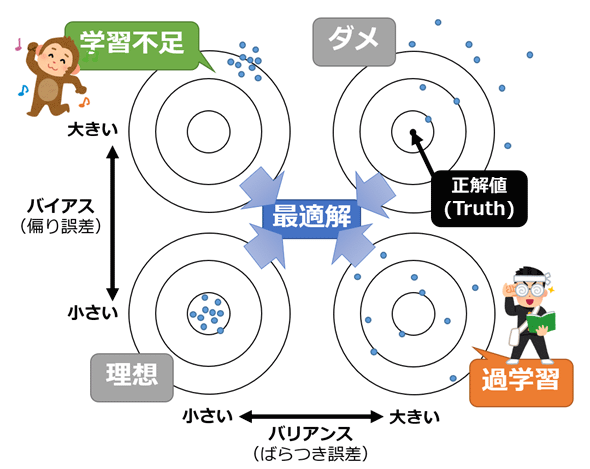
バイアスとバリアンス(分散)のトレードオフ。
-
バイアス-バリアンス分解:汎化誤差(平均二乗誤差など)の期待値をバイアス+バリアンス+ノイズの3つの和に分解すること。
https://ja.wikipedia.org/wiki/偏りと分散 -
ガウス=マルコフの定理:残差を最小にするように最小二乗法で求めた推定量が、最良線形不偏推定量になることを保証する定理。
https://ja.wikipedia.org/wiki/ガウス=マルコフの定理 -
クラメール・ラオの不等式:不偏推定量の分散の下限(バイアスの期待値は0なので不偏推定量の下限)を知れる。
-
クラメール・ラオの下限:クラメール・ラオの不等式によって求められる不偏推定量の分散の下限
-
有効推定量:クラメール・ラオの下限を満たす推定量。最も分散の小さい不偏推定量といえるので、優れた推定量と言える。
-
フィッシャー情報量:フィッシャー情報量によって、クラメール・ラオの不等式を求められる。また、最尤推定量は対数尤度関数の母数偏微分の二乗の期待値なので、V[X]=E[X^2]-(E[X])^2が使える。https://www.youtube.com/watch?v=3yE5PrfNVrk
クラメール・ラオの不等式とフィッシャー情報量が重要なのは、推定量の優秀さ(有効推定量であるか)を調べられるから。
-
十分統計量:ある統計量(標本平均など)を定めると、母数(母平均など)を定めなくても、どのような標本が得られるかの確率が定まるような統計量(標本平均など)。
例えば、分散が既知の正規分布だと、標本平均が定まれば、母平均が定めなくても、ある程度どのような標本が得られるかは分かる。だが、最小値が定まっても、ある程度どのような標本が得られるかは分からない。
https://youtu.be/9i8b_zx8_kA?si=D5B9jtFkT0DA_ys9 -
フィッシャー・ネイマンの分解定理:十分統計量であれば、今の標本が得られる尤度関数(同時確率分布)
L(θ)=f(x_{1},x_{2},\cdots,x_{n};θ)=f(x;θ)
https://www.youtube.com/watch?v=sIKsbKO1Gmo -
一致性:サンプルサイズが無限大になった時に、推定量が母数に一致すること。
https://bellcurve.jp/statistics/glossary/12813.html
不偏性と一致性の違い。
- 漸近分布:標本サイズnを∞にした時に収束する分布。標本平均なら
(\mu,\sigma^2/n) - 漸近分散:漸近分布の分散。標本平均なら
\sigma^2/n - 漸近有効性:推定量(標本平均など)の漸近分散が、クラメール・ラオの下限と一致していれば、推定量に漸近有効性があると言える。つまりnを∞にした時、推定量の分散が最小になる=優れた推定量と言える。
- 漸近正規性:nを∞にした時、正規分布に分布収束すること。つまり、分散は0に収束するので偉い。
最尤推定量はの一致性、漸近有効性、漸近正規性を持つので、とてもいい推定量と思える。しかし、不偏性を持つとは限らない。
-
ジャックナイフ法:不偏でない推定量(推定量の期待値が母数にならないのでバイアスは0にならない)を補正して、不偏推定量に近づけることができる。補正した推定量をジャックナイフ推定量という。アルゴリズムとしては、1つ標本を除いた部分標本の推定量を全ての標本を求め、その平均を推定量とするというシンプルなもの。https://qiita.com/nijigen_plot/items/cb7a51b4c42349a1d0a0
-
リサンプリング法:ジャックナイフ法のように部分標本を用いて、推定精度を向上させる方法全般。ほかに有名なものとして、ブートストラップ法がある。
9.区間推定 2/6
母分散の比の検定: 多項分布の区間推定:母比率の区間推定に近い。 多項分布の差の区間推定:母比率の差の検定に近い。比率同士が独立でないので共分散が入ってくる。https://bellcurve.jp/statistics/course/18227.html テキストのE[N1N2]=n(n-1)p1p2の解説。テクニカルなので自分で導出は大変。これは多項分布でしか成り立たないので注意が必要。
10.検定の基礎と検定法の導出 5/6
抜取検査のFP(合格品を不合格にする)が生産者危険、FN(不合格品を合格品にする)が消費者危険。
11.正規分布に関する検定 1/6
12.一般の分布に関する検定法 3/6
尤度比検定。
13.ノンパラメトリック法 1/6
ウィルコクソンの符号順位統計量の平均・分散
14.マルコフ連鎖 4/6
行が今の状態を表し、列が今その状態である時の未来の状態確率。
 例題の回答。
例題の回答。
15.確率過程の基礎 3/6
ブラウン運動では平均は変わらず、tが増えていくにつれて、分散も増えていく。
全体の解説
ブラウン運動、ランダムウォーク、ウィナー過程
ポアソン過程
ポアソン過程はウィナー過程と違い、上下動の幅ではなく発生頻度の幅が確率分布に従う。ウィナー過程では時間tが1増えるごとに、yが確率分布により生成された量分が増えていたが、ポアソン過程は時間tが確率分布により生成された量分増えたら、yが1増える。確率分布はウィナー過程は正規分布であったが、ポアソン過程は指数分布になる。
複合ポアソン過程
複合ポアソン過程は合計の終端に確率変数が使われているので理解が難しいが、ポアソン過程のyの増加量をUkとして変更できるようにしたものだと考えればいい。
ポアソン過程では増加量は1なのでUk=1で複合ポアソン過程はポアソン過程と同一になる。
16.重回帰分析 8/6
17.回帰診断法 1/6
18.質的回帰 1/6
ロジスティクス回帰 プロビットモデル
19.回帰分析その他 1/6
全体像 打ち切りモデル 生存時間解析の全体像
比例ハザード性
20.分散分析と実験計画法 7/6
問20.6は説明不足なのでこの記事が参考になります。
21.標本調査法 3/6
22.主成分分析 4/6
23.判別分析 4/6
分類。 問23.3(1)はめちゃくちゃ難しくて解説も不十分です。
24.クラスター分析 2/6
クラスタリング。
25.因子分析・グラフィカルモデル 5/6
因子分析 共通性の解説。
26.その他の多変量解析手法 0/6
27.時系列解析 7/6
-
弱定常過程(共分散定常過程)、ホワイトノイズ
https://tjo.hatenablog.com/entry/2013/07/04/190139 -
p次自己回帰過程[AR(p)]、q次移動平均過程[MA(q)]、(p,q)次自己回帰移動平均過程[ARMA(p,q)]、(p,1,q)次自己回帰和分移動平均過程[ARIMA(p,1,q)]
- 全体
https://tjo.hatenablog.com/entry/2013/07/12/184704
https://otexts.com/fppjp/arima.html - ARモデル 期待値、分散、自己共分散の導出
https://messefor.hatenablog.com/entry/2020/08/14/191709
https://ja.wikipedia.org/wiki/自己回帰モデル - MAモデル 期待値、分散、自己共分散の導出
https://messefor.hatenablog.com/entry/2020/08/02/153338
https://ja.wikipedia.org/wiki/移動平均モデル - 反転可能性
https://messefor.hatenablog.com/entry/2020/08/12/130240 - ARMAモデル
https://ja.wikipedia.org/wiki/自己回帰移動平均モデル
ARMA
- 全体
-
単位根検定、ディッキー・フラー検定、拡張ディッキー・フラー検定
https://ja.m.wikipedia.org/wiki/単位根検定
https://ja.wikipedia.org/wiki/ディッキー–フラー検定 -
ラグオペレーター(バックシフトオペレーター)、ラグ多項式
-
状態空間モデル
-
自己相関関数(ACF)と偏自己相関関数(PACF)
-
ダービン・ワトソン検定、系列相関
https://syleir.hatenablog.com/entry/2022/05/15/152534
https://en.wikipedia.org/wiki/Durbin–Watson_statistic -
スペクトル密度関数(スペクトラム)、ペリオドグラム
http://www.mi.u-tokyo.ac.jp/mds-oudan/lecture_document_2019_math7/時系列解析(2)_2019.pdf
28.分割表 5/6
- 研究デザイン:前向き研究、後向き研究、コホート研究、ケースコントロール研究
https://bellcurve.jp/statistics/course/18127.html
これらの研究によって分割表がつくられることがある。
- 分割表:因子、水準
https://ja.wikipedia.org/wiki/分割表
https://best-biostatistics.com/contingency/contingency-kiso.html
分割表の評価にこれらの指標が使われる。
- オッズ比、対数オッズ比、標本オッズ比、相対リスク
大標本の母対数オッズ比が正規分布で近似できることを利用することで信頼区間を求められる。
分割表の検定ではこれらの手法が使われる。
-
適合度の検定、独立性の検定、カイ二乗統計量
https://qiita.com/m1t0/items/bcfc5f6b2c8697fea326
https://bellcurve.jp/statistics/course/9496.html
https://bellcurve.jp/statistics/course/9494.html -
尤度比検定、逸脱度
逸脱度は2×(対数尤度)
2元分割表の最尤推定量の導出(導出が難しいので暗記必須)
よって2元分割表の逸脱度はこうなる。これも暗記必須。
- フィッシャーの正確検定(サンプルサイズが小さいとき)
https://bellcurve.jp/statistics/course/23950.html
また、分割表の因子間の独立性や条件付き独立性を解析するためにこのようなモデルが使われる。
- 対数線形モデル(主効果モデル)
https://qiita.com/m1t0/items/11e6a271d3a46a3e5f4d
https://www.psy.ritsumei.ac.jp/hoshino/spss/log_00.html
https://en.wikipedia.org/wiki/Log-linear_analysis - I×Jの2元分割表:多項分布モデル、ポアソン分布モデル
- I×J×Kの3元分割表:完全独立モデル、周辺独立モデル、条件付き独立モデル、階層モデル
- グラフィカルモデル:部分グラフ、完全部分モデル、クリーク
29.不完全データの統計処理 3/6
30.モデル選択 1/6
31.ベイズ法 4/6
32.シミュレーション 2/6
問32.1(2)は解答。




Discussion