🤖

AIは新しい音響アルゴリズム発見の夢を見るのか - やってみたら発見したと言い張っている -

2025/04/08に公開

1件

 短いまとめAIに音声をMIDIに変換するアルゴリズムを「発見」させる実験をした
AIがアルゴリズムを提案→実装→評価→改善できる試験環境を作成しループさせた
実際に動くコードが生成され、測定可能な改善がみられた
新しいところはAIがアルゴリズムを考えるあたりぐらい

[https://zenn.dev/romot/articles/11edc86fb6ab11#aiがアルゴリズムを提案する]
コード: https://github.com/romot-co/mir-eval-autolab
!厳密性や意味のある結果かよりも「実際にアルゴリズム発見環境の構築は可能か？」を試しました。
!専門家ではないので評価がむずかしく、

AIが言い張っている「あたらしいアルゴリズム」がわずかでも新しいのかはわからないです。
正直、楽器鳴らしたり歌ったら、それにあわせてずんだもんが歌うのをつくりたいだけなったのに、Vibeに乗っていたらこうなった。

 はじめに
AIくんは人間越えてるしシンギュラリティだぞみたいな話をよく見ます。

でも実際やってみるとどこかで見たことあるようなコピペ的なものばかりしかつくってくれません。
とはいえ本当にAIが「新しいアルゴリズム」を自動で見つけ出したら面白いし意味あるよなあと思い、実際に試してみました。

AIに新しい音楽用アルゴリズムを「発見」させようとした素人のログです。

 背景と課題私は作曲を趣味とするUIデザイナー/フロントエンジニアですが、本格的な音響処理のアルゴリズムは専門外です。FFT？ゲームだっけ？ぐらいです。
しかし諸々の事情で「音をMIDIノートに変換するライブラリ」が欲しかったのですが、
既存のMIDI変換ライブラリを調査した結果：
ほとんどがオフライン処理（リアルタイム非対応）
精度が低い、もしくは商用製品で高価
オープンソースの選択肢が限られている
つらいし自作は無理だし……なので、

AIが「アルゴリズムを考えられるか」を試すことにしました。

 どういう仕組みにすればいいのか
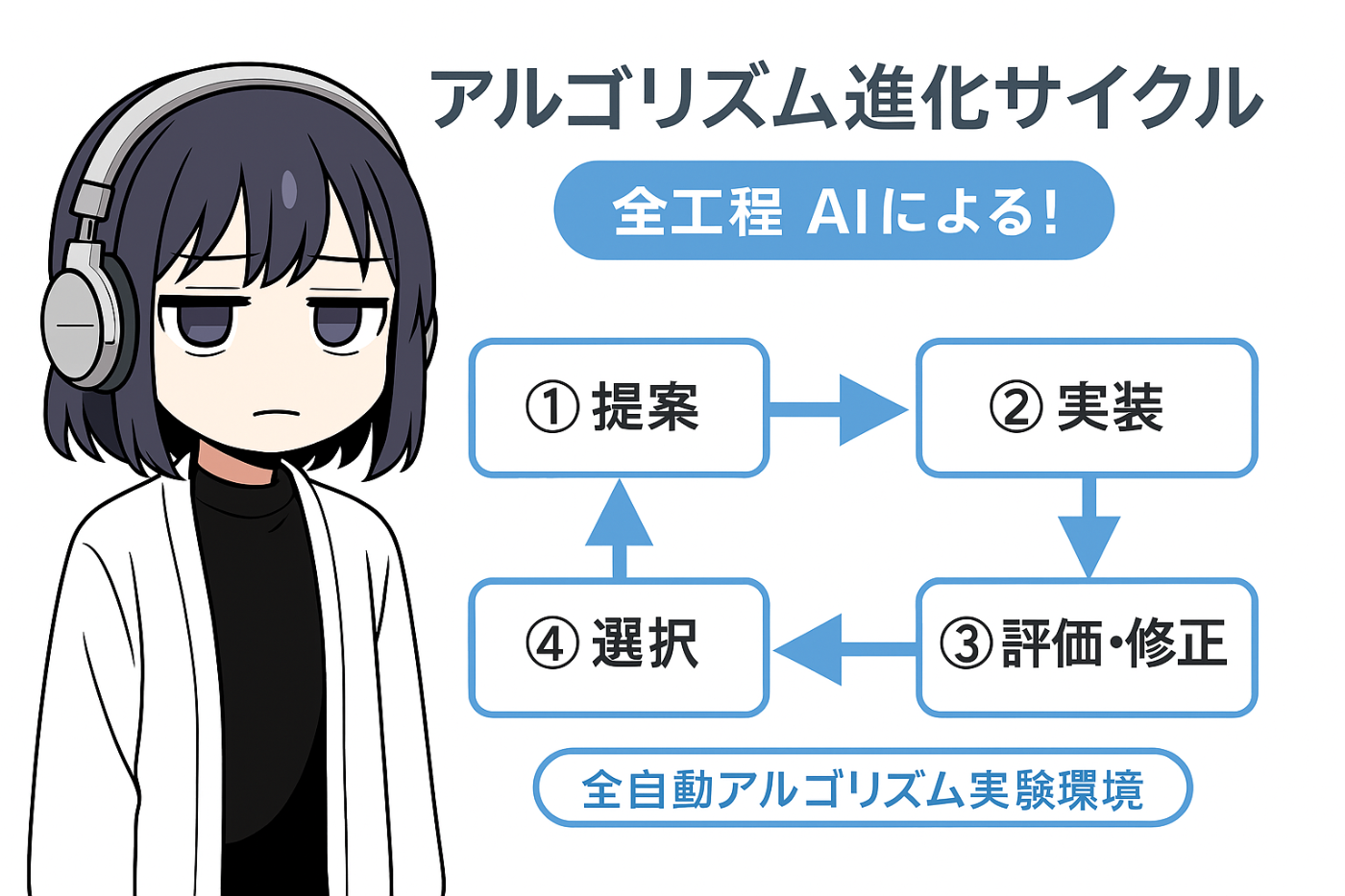
とはいえ、AIはアルゴリズムを考えることは出来だろうものの。

本当に良いのか悪いのか、どう評価すればいいのか分かりません。
そこで見つけたのがMIR_EVALというライブラリ。

音が始まるタイミングやピッチの精度やノート化の精度を評価できるものです。
このF値を評価指標に取れば自動アルゴリズム生成できるんじゃない？と考えました。

評価点は以下にしてみました。

オンセット検出：音がいつ始まるか

オフセット検出：音がいつ終わるか

ピッチ検出：音の高さ（単音）

マルチピッチ検出：複数の音が同時に鳴っている場合の各音の高さ

ノート検出：オンセット、オフセット、ピッチの組み合わせ
!できるのか？が主目的なので、多少間違っていようが、実性能でなくてもいいか！という精神です。

 AIによるアルゴリズム生成および評価試験環境をつくる試した方法はこんな感じです：
AI（ChatGPTやClaude）にアルゴリズム案を10個ほど提案してもらう
提案された案をAIが実装してMIR_EVALで評価（F値を記録）
評価結果をAIに渡し、コードの改善案をもらう
改善版を再評価
結果が良ければさらにパラメータを調整して評価
結果を比較して良いものを採用、悪いものは破棄
このループを繰り返してアルゴリズムを進化させる
要するに、AIがアルゴリズム提案して、AIが実装して、AIが評価試験して、AIが良いものを選ぶという流れです。AIが「新しいアルゴリズム」を発見できるのか、実験です。
パラメータではなくアルゴリズム自体をAIが考えるというところがちょっと新しいところでしょうか。

 実験環境をつくってデータを集める
 評価のためのスクリプトを作成このあたりはMIR_EVALのラッパーを半分手動で(その後ほぼAIくんが)つくりました。

 評価指標となるデータが必要動けばいいので、試験ではまずは合成データを使いました。
22個の合成データ生成スクリプト

 指標にできそうなもの軽量な実音源: TRIOS

クソデカピアノデータ: Maestro
実際にはTRIOSも利用しました。

 AIがアルゴリズムを提案するLLMが出した提案は、具体的には以下のようなアルゴリズムが提案されました(何度かの改善イテレーション後)

# PZSTDDetector アルゴリズム仕様書

## 1. はじめに

**楽音信号の複数音同時推定（マルチピッチ推定）は**、自動採譜やミュージックインフォメーションリトリーバル分野において重要な研究課題の一つである。典型的な手法では、周波数スペクトルからピークを抽出し、倍音構造に基づいたF0（基本周波数）の同定を行うアプローチが多い。しかし、周波数スペクトルのみでは**位相情報やフレーム間連続性**を十分に活用できないため、雑音混入や倍音干渉の多い状況では誤検出が生じやすい。

そこで本研究（本実装）では、**時間軸の位相安定度を評価するSPOD (Spectral Phase Offset Density)** を導入し、雑音的成分と定常的な楽音成分をより明確に区別する。また、新たに**HCF (Harmonic Coherence Flux)** と呼ばれる機構を導入して、楽音の**倍音整合性**や**時間的変化（オンセット・オフセット）**を強調する。本アルゴリズムを総称して、**PZSTD (Phase-Zero-crossing-based Spectral/Temporal Detector)** と位置づけ、以下の目標を掲げる。

1. **目的**  
   - **複数同時に存在するピッチ**（周波数）を正確に検出したい。  
   - オンセット（音の開始）やオフセット（音の終了）タイミングを高精度に推定したい。  
   - 雑音的成分や倍音干渉による誤認を極力低減したい。  

2. **提案手法の主な特徴**  
   - **SPOD** を用いた位相安定度マップにより、定常度の低い雑音やブレス音などを抑制し、**位相の安定した楽音ピーク**を強調。  
   - **HCF** によりフレーム間のコヒーレンス変化を数値化し、**急激な変化をオンセット指標**と捉えてノート開始位置を補足。  
   - 倍音構造を考慮したスコアリング(マルチピッチ推定)と、線形割り当て手法による**ノート追跡**を組み合わせ、フレームを通じた安定したノート列を生成。
...
全文以下に、本アルゴリズム（PZSTDDetector）の概念・目的から手法・実装の詳細までを、「論文風」の形式で分かりやすく包括的にまとめたアルゴリズム仕様書を示します。要所では数式や図示的なイメージを織り交ぜて、SPOD (Spectral Phase Offset Density) と HCF (Harmonic Coherence Flux) の考え方・目的・手順を整理し、マルチピッチ推定・ノート検出の全体像を解説します。

 PZSTDDetector アルゴリズム仕様書
 1. はじめに楽音信号の複数音同時推定（マルチピッチ推定）は、自動採譜やミュージックインフォメーションリトリーバル分野において重要な研究課題の一つである。典型的な手法では、周波数スペクトルからピークを抽出し、倍音構造に基づいたF0（基本周波数）の同定を行うアプローチが多い。しかし、周波数スペクトルのみでは位相情報やフレーム間連続性を十分に活用できないため、雑音混入や倍音干渉の多い状況では誤検出が生じやすい。
そこで本研究（本実装）では、時間軸の位相安定度を評価するSPOD (Spectral Phase Offset Density) を導入し、雑音的成分と定常的な楽音成分をより明確に区別する。また、新たにHCF (Harmonic Coherence Flux) と呼ばれる機構を導入して、楽音の倍音整合性や**時間的変化（オンセット・オフセット）**を強調する。本アルゴリズムを総称して、PZSTD (Phase-Zero-crossing-based Spectral/Temporal Detector) と位置づけ、以下の目標を掲げる。
目的

複数同時に存在するピッチ（周波数）を正確に検出したい。
オンセット（音の開始）やオフセット（音の終了）タイミングを高精度に推定したい。
雑音的成分や倍音干渉による誤認を極力低減したい。
提案手法の主な特徴

SPOD を用いた位相安定度マップにより、定常度の低い雑音やブレス音などを抑制し、位相の安定した楽音ピークを強調。

HCF によりフレーム間のコヒーレンス変化を数値化し、急激な変化をオンセット指標と捉えてノート開始位置を補足。
倍音構造を考慮したスコアリング(マルチピッチ推定)と、線形割り当て手法によるノート追跡を組み合わせ、フレームを通じた安定したノート列を生成。
以下では、本アルゴリズムの構成要素と各プロセスを順に詳述する。

 2. アルゴリズム全体概要図示的に示すと、アルゴリズムの流れは次のステップで構成される（図がある場合を想定）:
STFT（時間-周波数変換）

SPODの計算（位相安定度マップ）
スペクトルピーク検出 + サブビン補間

F0候補群の事前生成（セント単位の離散化）
フレーム内F0推定（スコアリング）

HCF (Harmonic Coherence Flux) マップ生成 + 平均SPODマップ (AvgHarmonicSPOD)

オンセットフレーム検出（HCF指標による）
フレーム間トラッキング（線形割り当て）
ノート開始・終了の決定（連続性、HCF/Coherence参照）

ノートのポストプロセス（短いノート除去、類似ピッチノートの結合 など）
最終的に、[ (開始時刻, 終了時刻), ピッチ(Hz) ] の形式でノート集合を出力する。

 3. SPOD (Spectral Phase Offset Density) のコンセプト
 3.1. 目的SPOD とは、「時間軸でみた位相の安定度」を定量化して 0～1 の範囲で表すスコアである。雑音的な成分や瞬時周波数が激しく変動する成分を抑制し、楽音的に定常度の高い成分（振幅が安定して振動している部分）を強調するために用いられる。

 3.2. 計算方法位相スペクトルの算出

音声データ ( x[n] ) に対してSTFTを行い、複素スペクトル ( S(k,m) ) から位相 (\Phi(k,m) = \arg(S(k,m))) を取得する。ここで ( k ) は周波数ビン、( m ) はフレームインデックス。
位相アンラップと差分

フレーム方向に位相をアンラップし、

[

\Delta \Phi(k,m) = \Phi_{\mathrm{unwrap}}(k,m+1) - \Phi_{\mathrm{unwrap}}(k,m)

]

を求める。これにより、フレーム間の位相変化（瞬時周波数）を取り出す。
移動分散の算出

上式の差分をある窓長（例: spod_window_sec 相当のフレーム数）で移動平均・ガウス平滑し、その分散

[

\sigma^2_{k,m} \approx \overline{\Delta \Phi(k,m)^2} - \bigl(,\overline{\Delta \Phi(k,m)},\bigr)^2

]

を計算する。分散が小さいほど位相が安定していると解釈できる。
指数変換によるスコア化

[

\text{SPOD}(k,m) = \exp\bigl(-\alpha,\sigma^2_{k,m}\bigr)

]

として 0～1 にマッピングする。ここで (\alpha) はハイパーパラメータ (例: spod_alpha)。分散が大きい部分は 0 近傍になり、分散が小さい定常成分は 1 に近い値となる。
以上により得られた SPODマップ は、「どの周波数ビンが、どのフレームで位相安定か」を可視化した指標となる。

 4. HCF (Harmonic Coherence Flux) のコンセプト
 4.1. 目的複数の楽音成分が同時に存在するとき、各F0とその倍音群が時間的にどの程度安定・協調しているかを示す指標として Harmonic Coherence を導入する。さらにフレーム間差分のFluxを取ることで、音の開始（オンセット）や減衰（オフセット）などの急激な変化をスパイク状に捉え、ノート開始・終了検出を補助する。

 4.2. Harmonic Coherence と Amplitude Sumフレーム (m)、あるF0候補 (f_0) に対して、上から計算したSPODおよび振幅スペクトル ( A(k,m) ) を倍音周波数でサンプリングし、次の2種類の値を算出する：
Harmonic Coherence ( C(f_0,m) )

倍音数 ( h ) (1～(H_{\max})) とし、各倍音周波数

[

f_h = h \cdot f_0 \cdot \sqrt{1 + \beta h^2} \quad (\beta = \text{inharmonicity factor})

]

でのSPOD値を取り、重み付き平均する。

[

C(f_0,m) = \frac{\sum_{h=1}^{H_{\max}} w_h ,\mathrm{SPOD}(f_h, m)}{\sum_{h=1}^{H_{\max}} w_h}

]

ここで ( w_h ) は倍音次に応じた重み（例: ( 1 / (h + \epsilon)^\gamma )）。高いほど倍音のコヒーレンスが強い（位相的に安定）。
Amplitude Sum ( A_{\text{sum}}(f_0,m) )

同じく倍音周波数を辿り、振幅スペクトル ( A(k,m) ) を線形補間して合計または平均する。

[

A_{\text{sum}}(f_0,m) = \sum_{h=1}^{H_{\max}} w_h , A(f_h,m)

]

 4.3. Flux とオンセット指標 ( O(m) )フレーム間の差分を取り、正の変化量のみを合計してFluxとする：
[

\Phi_{C}(f_0,m) = C(f_0,m) - C(f_0,m - \Delta_n), \quad

\Phi_{A}(f_0,m) = A_{\text{sum}}(f_0,m) - A_{\text{sum}}(f_0,m - \Delta_n)

]

[

\Phi_{\mathrm{comb}}(f_0,m) = w_C ,\max{0,\Phi_C(f_0,m)}
w_A ,\max{0,\Phi_A(f_0,m)}

]
これを全F0候補 ( f_0 ) 方向に総和すると、フレームごとのオンセット指標 ( O(m) ) が得られる：
[

O(m) = \sum_{f_0} \Phi_{\mathrm{comb}}(f_0,m)

]
この ( O(m) ) が大きいフレームは、何らかの楽音成分が新規に立ち上がった可能性が高いと解釈できる。よって find_peaks 等でピーク抽出し、HCFベースのオンセットフレームとして利用する。

 5. 処理手順の詳細
 5.1. STFT およびスペクトル取得音声信号 ( x[n] ) を STFT し、複素スペクトル ( S(k,m) ) を得る。
振幅 ( A(k,m) = |S(k,m)| ) と位相 (\Phi(k,m) = \arg(S(k,m))) を取得。
STFTパラメータ例:
n_fft = 2048
hop_length = 1024
window = 'hann'

center = True (librosaデフォルト)


 5.2. SPODマップ生成位相スペクトル (\Phi(k,m)) をフレーム方向に unwrap し、差分 (\Delta \Phi(k,m)) をとる。
ガウス平滑や移動平均で分散 (\sigma^2_{k,m}) を近似計算。
(\exp(-\alpha,\sigma^2_{k,m})) により0～1にマッピングし、SPOD(k,m) を得る。

 5.3. ピーク検出とサブビン補間各フレーム ( m ) について、振幅スペクトル ( A(k,m) ) と SPOD ( \mathrm{SPOD}(k,m) ) を組み合わせて閾値判定（dB閾値、SPOD閾値、ピークプロミネンス等）し、ピークビンを検出する。
放物線近似でサブビン精度のピーク周波数を補間し、(周波数, 振幅, SPOD) の三つ組で保持する。

 5.4. F0候補群の離散化とスコアリングある周波数範囲（例: 30Hz~5000Hz）をセント単位で細分化し、F0候補 ({f_0^{(i)}}) を用意する。
各フレームで検出されたピーク群に対し、各F0候補の「倍音一致度 + 連続性ボーナス」などからスコアを計算。
倍音周波数がピークと近ければ加点。ピークのSPODが高ければさらに加点。
前フレームでの同じF0近傍が存在していれば連続性としてボーナス。

最高スコアのF0を1つ選び、それがしきい値 (f0_score_threshold) を超えれば採用し、説明されたピークを除去して再度スコアリングを行うことで複数F0を取り出す。

 5.5. HCFマップの計算
SPODマップ・振幅スペクトル・F0候補から、前述の ( C(f_0,m) ) と ( A_{\text{sum}}(f_0,m) ) を各フレーム・各F0候補について計算。
フレーム差分を取り、Flux ( \Phi_{\mathrm{comb}}(f_0,m) ) を得る。
(\Phi_{\mathrm{comb}}(f_0,m)) を ( f_0 ) 方向に合計して (O(m)) を導出。
(O(m)) を正規化し、find_peaks 等で閾値を超えるピークフレームをオンセットフレーム候補として抽出。

 5.6. ノート開始（オンセット）判定フレーム単位で推定された F0リストのうち、HCFオンセットフレームであって、さらにSPOD平均値(AvgHarmonicSPOD) が高い(あるいは一定閾値を超える) 場合のみ、新規ノート開始を許可する。
HCFオンセットフレームでなければ、基本的に新しいノートトラックを開始しない（誤検出を抑制）。

 5.7. ノートトラッキングとオフセット判定フレーム (m) の F0集合 と、アクティブなノートトラックとの間で線形割り当て (Hungarianアルゴリズム) を行い、最適対応を得る。
対応が得られなかったノートはオフセットとみなし、そこで終端時刻を確定する。
オフセットの早期判定として、Coherence ( C(f_0,m)) が閾値以下になった際にオフセットを先行させることもある。

 5.8. ポストプロセス短すぎるノート（ min_note_duration_sec 未満）は削除する。
近接ピッチ（ note_merge_tolerance_cents）かつ隣接フレームギャップが小さいノートは結合する。
ピッチ変動が大きく分散が非常に大きいノートは除外する（max_pitch_std_dev_cents など）。
最終的に、(開始時刻, 終了時刻, ピッチHz) のノートリストが得られる。

 6. 考察・利点
SPOD による位相安定度評価により、ホワイトノイズや擦過音、パーカッシブな成分などフレーム間で位相が急変する成分を排除しやすくなる。結果として、雑音や過密倍音がスペクトル上に存在する状況下でも、楽音成分のみをピークとして捉えやすい。

HCF は、楽音の倍音構造に基づく安定性と、そのフレーム間差分（Flux）を同時に見るため、通常のオフセット／オンセット検出器より倍音協調度に敏感である。これにより、正確なオンセット推定が可能となり、短いノートの不定期な出現や減衰端をより適切に扱える。
ピッチ推定（F0推定）とノートトラッキングを明確に分離し、かつ線形割り当てによりフレーム間の継続性をコスト最小化で解決しているため、音が多少周波数変動していても1つのノートとして捕捉しやすい。
Inharmonicity Factor (\beta) を導入することで、ピアノ弦などの倍音がわずかに高い周波数へシフトする現象をモデル化。調弦誤差や楽器固有の倍音構造への耐性を向上。

 7. パラメータ設定例
STFT

n_fft = 2048, hop_length = 1024, window = 'hann'


SPOD

spod_window_sec = 0.07, spod_alpha = 1.1

min_peak_spod_stability = 0.15 (ピークとして採用する最小SPOD閾値)


F0候補離散化
周波数範囲: 30～5000 Hz
解像度: 15 cents 刻み


HCF

hcf_max_harmonics = 10~12
hcf_inharmonicity = 0.0001

hcf_tau_sec = 0.01  (フレーム差分の時間幅)


オンセット検出

hcf_onset_peak_thresh = 0.12 ( (O(m)) のピーク検出閾値 )

hcf_spod_onset_thresh = 0.3  ( 平均SPODがこれ以上で初めてオンセット成立 )


ポストプロセス
min_note_duration_sec = 0.05
note_merge_tolerance_cents = 50
max_pitch_std_dev_cents = 40


 8. 結論以上のアルゴリズムにより、時間領域の位相安定性 (SPOD) と 倍音構造の時間変化 (HCF) を組み合わせることで、雑音や不規則なスペクトル成分を効果的に抑制し、音楽信号における複数同時音の開始時刻・終了時刻・ピッチを安定的に推定できる。特にオンセット付近のコヒーレンス変化を精密にキャッチできる点が大きな利点であり、複数声部（ポリフォニー）解析において有効性が期待される。
本アプローチは、以下のような拡張が考えられる。

異なるInharmonicity Factor を各F0ごとに動的推定

SPODの別種定義（例：変調スペクトルを用いたより精緻な位相安定度評価）

Machine Learning との組み合わせによるパラメータ動的最適化
いずれにせよ、位相情報の利用と倍音フラックスの観点は、既存手法に対して堅牢性と精度向上をもたらす可能性が高い。

 最後に本仕様書では、PZSTDDetector が内部的にどのように位相安定性の評価 (SPOD) と倍音時間変化 (HCF) を組み合わせ、マルチピッチ推定とノート検出を行っているかを、コンセプトと数式ベースで示した。

目的が「複数同時音の正確なピッチ推定とノートセグメンテーション」であることが明快であり、SPOD と HCF の概念が「位相の安定性を測定する指標」「倍音コヒーレンスのフレーム差分からオンセット検出を行う指標」という形で単純化されているので、全体の処理フローも理解しやすい。本手法は、実際の音楽信号の複雑な倍音構造に対しても有効に機能し得ることが期待される。
がんばって読んでみたものの、なにを言っているかはだいぶわからなかったです！

 AIが評価する## PZSTDDetector アルゴリズムの新規性要約

PZSTDDetector は楽音信号の複数音同時推定において、二つの革新的要素を導入しています。

- 一つ目は「時間軸の位相安定度」を評価するSPOD機構で、従来の振幅スペクトルだけでなく位相情報を活用して雑音と楽音を区別します。
- 二つ目は倍音構造の時間的変化を捉えるHCF機構で、音の開始・終了を高精度に検出します。

これらを組み合わせることで、従来手法より複雑な音楽環境での精度向上が期待されます。特にピアノなど倍音構造が複雑な楽器音の分析に強みがあり、自動採譜やミュージックインフォメーションリトリーバル分野に貢献する新規性の高いアプローチといえます。
本当に妥当なのか、AIの評価は信用していいのかは、よく分かりません。

 AIが実装するなにもわからないまま実装されましたが、実際に動きました。

やはり何度かの改善イテレーション後です。
# --- PZSTDDetector Class ---

class PZSTDDetector(BaseDetector):
    """
    Refined PZSTD-based multi-pitch detector using Numba optimization.
    Allows grid search over onset detection parameters.
    HCF Enhanced: Integrates Harmonic Coherence Flux for improved onset/offset detection.
    """
...
    def _calculate_stft(self, audio_data: np.ndarray) -> Tuple[np.ndarray, np.ndarray, np.ndarray]:
        """Calculates STFT using fixed parameters."""
        if self._sr is None: raise RuntimeError("Detector not initialized. Call _initialize_run first.")
        try:
            S_complex = librosa.stft(audio_data,
                                     n_fft=self.n_fft, # Use instance var
                                     hop_length=self.hop_length, # Use instance var
                                     window=self.window, # Use instance var
                                     center=True)
            S_amp = np.abs(S_complex)
            S_db = librosa.amplitude_to_db(S_amp, ref=np.max(S_amp) if S_amp.size > 0 else 1.0, top_db=80.0)
            phases = np.angle(S_complex)
            self._times = librosa.frames_to_time(np.arange(S_complex.shape[1]), sr=self._sr, hop_length=self.hop_length) # Use instance var
            self._A_lin = S_amp
            return S_amp, S_db, phases
        except Exception as e:
            logger.error(f"Error calculating STFT: {e}", exc_info=True)
            self._times = np.array([])
            return np.array([[]]), np.array([[]]), np.array([[]])

    def _calculate_spod(self, phases: np.ndarray) -> np.ndarray:
        """Calculates the SPOD map using Gaussian filter."""
        n_bins, n_frames = phases.shape
        if n_frames <= 1 or self._sr is None: return np.zeros_like(phases)
        spod_window_frames = max(1, int(self.spod_window_sec * self._sr / self.hop_length)) # Use instance vars
        phi_unwrapped = np.unwrap(phases, axis=1)
        inst_freq = np.diff(phi_unwrapped, n=1, axis=1, append=phi_unwrapped[:, -1:])
        try:
            sigma = spod_window_frames / 4.0
            kwargs = {'sigma': sigma, 'axis': 1, 'mode': 'nearest'}
            inst_freq_sq_mean = gaussian_filter1d(inst_freq**2, **kwargs)
            inst_freq_mean = gaussian_filter1d(inst_freq, **kwargs)
            inst_freq_var = np.maximum(0, inst_freq_sq_mean - inst_freq_mean**2)
        except Exception as e:
            logger.error(f"Error calculating moving variance for SPOD: {e}", exc_info=True)
            return np.zeros_like(phases)
        spod_map = np.exp(-self.spod_alpha * inst_freq_var) # Use instance var
        return np.clip(spod_map, 0.0, 1.0)

    ...
全ソースはこちら

 AIが改善してパラメータを探すそして評価結果から勝手にアルゴリズム改善し、パラメータをサーチしてくれました。


評価指標
初期
改善後
改善率


オンセット検出 F値
47.0%
74.4%
58.3%向上

オフセット検出 F値
41.3%
76.9%
86.2%向上

ピッチ検出 F値
0%
65.2%
0%→65.2%

音符検出 F値
0%
63.0%
0%→63.0%

フレームピッチ分析 総合精度
1.3%
71.2%
5377%向上

とにかくF値ベースでは改善されました！

 AIがアルゴリズムをつくったと主張つくってくれたし動きはしました！

実際に組み込んでみた限り、性能はそんな高くない気もしますが、動きます。
感覚ベースだとこれほんとうに新しいのか……？

なんか調べた中ですら見たことあるような……？という強い疑念はあります。

 Claudeさんによるインタラクティブ解説仕様書とコードそのものを見せたら勝手に作ってくれた。

あっているかはわからないのですが。

https://claude.site/artifacts/44f882b9-3f13-4afe-8279-fc4b4397b228

 結論本当に意味がある結果なのかがわからない......という致命的な問題はありますが、

とにかく回ることは回りました！

 限界も感じた素人だと判断できないという点を除いても。
実際、この方法はちょっと用途が狭いかもしれません。

明確な評価指標があれば、直接機械学習した方が効率的な気もしますし、人間が試行錯誤する部分をAIが置き換える意義がどれほどあるのか疑問が残ります。
また、いくつか限界を感じた点があります：

評価指標が必須：ないと回らないと思います……

人間の介在が必要：完全自動化は難しいというか、はまったり、コードを壊したりデータの方を見てハックしようとすることがあるので、掃除役の人間が必要

評価環境構築が大変：専門知識がないと適切な評価環境を作るのが難しい
また、このループ加速は評価フィードバックがすぐ返ってくる場合にのみ有効でありそうです。

たとえばUIデザインのA/Bテストのような間に人間の評価が入るようなものは、可能ではあっても必然的に高速でのループはできなさそうです(実を言うとほんとの大元はこれをやりたかった)
地道な改善には向いているけど、抜本的な革新を生み出すには至らないのかもという印象です。
……まあそもそも専門的なことは分からないので、詳しい方から見るとツッコミだらけだと思います。

 可能性は感じる新発見や完全な自動化だとはあんまり言えませんが、AIが自動的にアルゴリズムを改良していくというプロセス自体には、確かに可能性を感じました。

速くてたくさん：とにかく速くて量が多い

別分野の知見を活かせる：別分野の知識を持ってきてくれそう

忘れられた技術ツリーを解放しそう：昔の技術を再度試してくれそう
いまはModelContextProtocolなども使って、

もっと試験環境のループ自体をどうにかできないか試しています。

 雑感とはいえAIはゼロから発明するというよりも、別の分野の知見を持ち込んだり、忘れられた技術ツリーを掘り起こしたりする方が得意という感覚を得ています。
これは「新発見」かは微妙に思えているのですが、分野横断的な知識の組み合わせという点では価値があると感じています。
ここまで読んでいただいてありがとうございました！

 リポジトリできたコードとかをGitHubにあげました。
GitHubリポジトリ（mir-eval-autolab）: https://github.com/romot-co/mir-eval-autolab

 絵ChatGPT

評価指標	初期	改善後	改善率
オンセット検出 F値	47.0%	74.4%	58.3%向上
オフセット検出 F値	41.3%	76.9%	86.2%向上
ピッチ検出 F値	0%	65.2%	0%→65.2%
音符検出 F値	0%	63.0%	0%→63.0%
フレームピッチ分析総合精度	1.3%	71.2%	5377%向上

Discussion

Romot

AIが考えた10の新しいアルゴリズム案：

https://github.com/romot-co/mir-eval-autolab/tree/main/algos

AIによる上記10の実装：

https://github.com/romot-co/mir-eval-autolab/tree/main/src/detectors
まともに動くのはごく一部でした。
そしてなによりも専門家じゃない限り評価も適切な利用も無理という実感。

Vibeにはまだ限界がありそうです。