🍫

毒チョコゲーム (Chomp) が先手必勝であることを Lean で証明する

に公開
テーマ「2025年の最も大きなチャレンジ」
定理証明支援系
lean
lean4
組合せゲーム
tech

こちらは、証明支援系 Advent Calendar 2025 17日目の記事です。
https://adventar.org/calendars/11438

毒チョコゲーム Chomp は先手必勝

毒チョコゲームとして知られる Chomp ゲームには、「プレーヤーが最善手を指した場合に先手必勝であることは証明されているが、具体的な必勝手を求めるのは難しい」という面白い特徴があります。
YouTube チャンネル「えびまラボ」の動画「毒チョコゲームの必勝法〖ゆっくり解説〗」では、この先手必勝性の証明について戦略盗用 (strategy stealing) という論法で分かりやすく解説されています。
https://youtu.be/agRtx_XREtA?si=9Zn_v44kdDU0Yo1P

この記事では、定理証明支援系 Lean 4 で Chomp ゲームを形式化し、ゲームが先手必勝であることを証明します。

Chomp（毒チョコゲーム）のおさらい

まずは普通の Chomp のルールをざっくり振り返ります。板チョコ(以降、盤面と呼びます)のイメージを示します。
Chomp ゲームの盤面
Chomp ゲームの盤面

  • 一番左上のピースが「毒チョコ」です
  • プレイヤーは交互に、好きなピースを 1 つ選び、そのピースより右下にあるすべてのピースをまとめて食べます(例えば、図中 p のピースを選ぶと灰色のピースをすべて食べます)
  • 最後に毒チョコを食べさせられたプレイヤーが負けとなります

半順序集合版 Chomp へ一般化

板チョコのような長方形の形のままでも、Chomp ゲームの形式化はできますが、ピースに 2 次元座標を入れたりと若干面倒な手順が入ってくるので、問題を少し一般化した、半順序集合版 Chomp を考えます。(動画の2:41)
板チョコの各ピースの集まりに、例えば下図のような半順序 (\le) の構造を入れることで、盤面を有限半順序集合(finite poset) とする Chomp ゲームの一般化を考えることができます。

  • 毒ピース = 最小元 \bot
  • 手番でできる操作 = あるピース p を選び、p \le q となるピース q をすべて取り除く
  • ゲームの盤面 = 有限半順序集合 (finite poset) の下に閉じた部分集合

最後の「ゲームの盤面」について、少し説明を加えます。ゲームが進行中の盤面は板チョコの右下部分が階段状に切り取られた形となります。
下に閉じた集合
このような盤面の形状は、半順序 \le の言葉で書くと「盤面のどのピース p に対しても、q \le p となるすべてのピース q も盤面に含まれている」という条件で表すことができます。すなわち、盤面を構成するピースの集合は \le について下に閉じています。

Lean による Chomp の形式化と先手必勝の証明

それでは、Lean 4 で半順序集合版の Chomp を形式化し、ある条件を満たす初期盤面においては、先手必勝であることを証明していきます。

証明の全体は以下のリンク先に掲載しています。
https://live.lean-lang.org/#url=https%3A%2F%2Fgist.githubusercontent.com%2Frikitoro%2F58dcc5230be0928decb50ccf67bf24f1%2Fraw%2FPosetChomp.lean

なお、本記事での証明では、Lean バージョン 4.22.0 より導入された grind タクティクを使用します。grind は強力な証明自動化タクティクで、証明に必要な定理を登録していくことも簡単できます。grind タクティクについてはこちらのページが詳しいです。

https://lean-ja.github.io/lean-by-example/Tactic/Grind.html

準備

この証明では、Lean の数学ライブラリ Mathlib を用います。特に、ピースの集合が有限の半順序集合となるので、Finset (有限集合) や PartialOrder (半順序集合) などに関する定義や定理が示されたライブラリをインポートしておきます。

import Mathlib.Data.Finset.Basic
import Mathlib.Data.Finset.Card
import Mathlib.Order.Basic

ピースを表す型変数 α を変数として用意しておきます。

variable {α : Type}  -- 各ピースの型：最小元(毒ピース)を持つ半順序集合
  [PartialOrder α] [OrderBot α] [DecidableEq α] [DecidableLE α]

ピースの集合が、最小元 (毒ピース) を持つ半順序集合となることを反映して、型α には、型クラス PartialOrder と OrderBot のクラスインスタンスとしています。また、型クラス DecidableEq と DecidableLE のクラスインスタンスであることも要求しています。これらは、ゲームの手を進める際に、盤面のピースを条件に従って取り除いたりするために必要となります。(端的に言うと Finset.filter を使うためです)

盤面 Board の定義

ゲームの盤面の型 Board α を定義します。この Board α は、盤面に残っているピースの(有限)集合 pieces と、それが満たすべき 2 つの条件

  • hasBot : \bot (毒ピース) が pieces に含まれている
  • downClosed : pieces は \le について下に閉じている

の証明から構成される構造体として定義します。

structure Board (α : Type) -- α は各ピースを表す型
  [PartialOrder α] [OrderBot α] [DecidableEq α] [DecidableLE α]
  where
  pieces : Finset α     -- 残っているピースの(有限)集合
  hasBot : ⊥ ∈ pieces -- 毒ピースが含まれる
  downClosed : -- 残っているピースの集合は下に閉
    ∀ p q, p ∈ pieces → q ≤ p → q ∈ pieces

ピースの有限集合は pieces は Finset α 型の値として定義しています。 なお、Finset をインポートしているので、\in や {...} などの集合で用いられる各種の記法が使えるようになります。

後のために、盤面のサイズをピースの個数で定義し、Board α を SizeOf クラスのインスタンスとしておきます。Finset.card を用いて、pieces の要素の個数を取得しています。

/-- 盤面のサイズを定義 (残っているピースの個数) -/
instance Board.SizeOf: SizeOf (Board α) where
  sizeOf b := b.pieces.card

毒ピース \bot のみからなる最終盤面 terminal αは、Board α 型の項として次のように定義できます。

/-- 毒ピースのみの最終盤面 -/
@[simp, grind]
def Board.terminal (α : Type)
  [PartialOrder α] [OrderBot α] [DecidableEq α] [DecidableLE α]
  : Board α where
  pieces := {⊥} -- ⊥だけを含む集合
  hasBot := by grind
  downClosed := by
    intro p q hqp
    simp_all

pieces は \bot だけを含む集合 (シングルトン) となります。
hasBot には、pieces に \bot が含まれていること、すなわち \bot \in \{\bot\} の証明を与えます。これは (人間にとっては) ほぼ自明ですが、grind タクティクを用いて証明しました。ちなみに、grind を grind? に置き換えると裏で使われている定理がわかります。ここではFinset.mem_singleton が使われていました。
downClosed には \{\bot\} が \le について下に閉じていることの証明を与えます。これは \le の反射律から導かれます。

与えられた盤面 b が最終盤面であることを表す述語 isTerminal b も用意しておきます。

/-- 最終盤面であることを表す述語 -/
def Board.isTerminal (b : Board α) : Prop :=
  b = terminal α

合法手 legalMove の定義

プレーヤーが盤面 b からピース p を一つ選んで取って一手進めた新しい盤面 b^{\prime} を (some に包んで) 返す関数 move b p を定義します。盤面にないピースや \bot を選んでしまった場合に失敗 (none を返す) するよう、Option (Board α) 型の項を返す関数として定義します。

/-- 盤面 b から、ピース p を選んで取った盤面 b' を返す -/
@[simp, grind]
def Board.move (b : Board α) (p : α) : Option (Board α) :=
  if h : p ∈ b.pieces ∧ p ≠ ⊥ then -- 合法手の場合 some b' を返す
    --
    let pieces := { q ∈ b.pieces | ¬ p ≤ q } -- p 以上のピースを取り除く 
    let hasBot : ⊥ ∈ pieces := by
      simp [pieces]
      cases b with grind
    let downClosed : ∀ p q, p ∈ pieces → q ≤ p → q ∈ pieces := by
      cases b with grind
    --
    some <| .mk pieces hasBot downClosed -- some b'
  else -- 合法手でない場合 none を返す
    none

プレーヤーが盤面に含まれるピース p (\ne \bot) を選んだ場合は、もとのピースの集合から p \le q となるピース q を取り除いた盤面 b^{\prime}を作り、some b' を返します。この新しい盤面 b^{\prime} のピースの集合 pieces は、内包記法を使って { q ∈ b.pieces | ¬ p ≤ q } と定義しています。hasBot と downClosed は grind タクティクを使うと簡単に証明できます。

次に定義する legalMove b b' は、盤面 b から b^{\prime} への合法手がある (すなわち b から b^{\prime} へmove 一手で移ることができる) という述語です。

/-- 盤面 b から b' への合法手がある -/
@[simp, grind]
def Board.legalMove (b b' : Board α) : Prop :=
  ∃ p, b.move p = some b'

ここで、「合法手を一手進めると盤面のサイズが必ず小さくなる」ことを証明しておきます。一手進めると少なくとも 1 ピースは食べるので、直感的には明らかですね。この定理 move_size_lt は、次に定義する盤面が勝ち盤面であるという述語 winning を再帰的に定義する際に必要となります。

/-- 一手進めると盤面のサイズが小さくなる
  NOTE : winning の定義が整礎再帰であることを示す際に使う -/
@[simp, grind →]
theorem Board.move_size_lt {b b' : Board α} (h : legalMove b b') :
  sizeOf b' < sizeOf b := by
  simp_all
  obtain ⟨p, hp⟩ := h
  obtain ⟨hv, heq⟩ := hp
  apply Finset.card_lt_card
  simp_all [← heq, Finset.filter_ssubset]
  use p
  constructor
  · grind
  · rfl

勝ち盤面の定義

Chomp では、先手も後手も同じ盤面が与えられた時に取れる手の選択肢は全く同じものとなります。したがって、盤面に対して (先手後手に依存せず、その盤面を与えられたプレーヤーが) 必勝となるかどうかが決まります。

では、盤面 b が勝ち盤面である、すなわち、盤面 b が与えられたプレーヤーに必勝手がある、という述語 winning b の定義を考えてみましょう。
盤面 b が勝ち盤面ということは、「うまい一手をとると、相手に勝つことができない盤面を押し付けることができる」ということです。したがって、述語 winning b は次のように定義できそうです。

お気持ちコード
/-- 盤面 b が勝ち盤面である -/
def Board.winning (b : Board α) : Prop :=
  ∃ (b' : Board α), legalMove b b' ∧ ¬ b'.winning
  decreasing_by sorry

盤面 b から合法手 legalMove b b' で行ける盤面 b^{\prime} があって、その盤面 b^{\prime} は勝ち盤面にはならない、すなわち、¬ winning b' であるというふうに、再帰的に定義しています。
しかし、この定義はうまくいきませんでした。というのも、この winning のように再帰的な関数の定義では、再帰呼び出しの引数が小さくなっていること (整礎再帰であること) の証明が必要となるのですが、その証明を与えることができないためです。
上記の decreasing_by の部分で sizeOf b' < sizeOf b を証明する必要があるのですが、この定義では、legalMove b b' を証明の条件として得ることができず、sizeOf b' < sizeOf b を証明することができません。

次のように条件 legalMove b b' を存在量化の形で表現することで、winning をうまく定義することができます。

/-- 盤面 b が勝ち盤面である -/
@[simp, grind]
def Board.winning (b : Board α) : Prop :=
  ∃ (b' : Board α) (_ : legalMove b b'), ¬ b'.winning
  decreasing_by grind

この定義では、decreasing_by において legalMove b b' を仮定に取ることが可能となり、先に示した定理 move_size_lt を使うことで、sizeOf b' < sizeOf b を証明することができます。実際の証明は grind タクティクで通ります。
ちなみに、この定義による winning b と ∃ (b' : Board α), legalMove b b' ∧ ¬ b'.winning が等価であることは簡単に証明することができます。

与えられた盤面 b が負け盤面であるという述語 losing b を winning b の否定として定義しておきます。

/-- 盤面 b が負け盤面である -/
@[simp, grind]
def Board.losing (b : Board α) : Prop :=
  ¬ b.winning

さて、毒ピース (\bot) だけからなる最終盤面 terminal α は負け盤面であるはずです。この事実は次のように証明できます。

/-- 最終盤面は負け盤面 -/
theorem Board.terminal_losing :
  terminal α |>.losing := by
  grind

初期盤面の特徴 (真の最大元を持つ盤面)

2次元長方形の初期盤面での Chomp では、1 \times 1 の自明な場合を除き、先手必勝となるのでした。このような盤面は、一番右下のピース、すなわち、半順序 \le における最大限 ttop を持ちます。

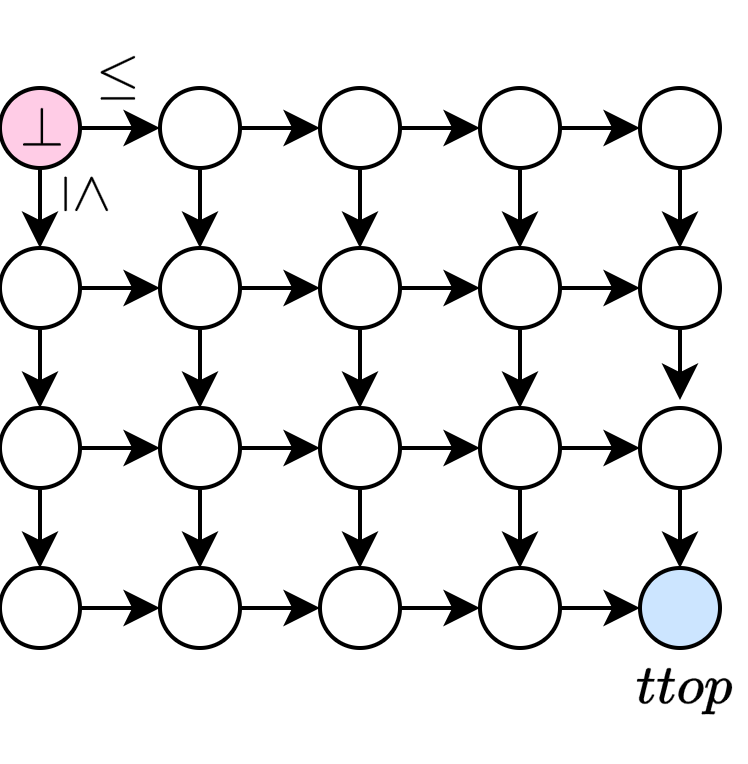
真の最大元を持つ盤面

一般の半順序構造での Chomp においても、最小元 (\bot) と異なる最大元 (ttop) を持つ盤面は勝ち盤面 (その盤面が与えられたプレーヤーが勝つ) となります。以降、最小元とは異なる最大元のことを真の最大限と呼ぶこととします。

盤面 b に真の最大限が存在するという述語 hasTop b を定義しておきます。

/-- 真の最大元(最小元と異なる最大元)が存在する -/
def Board.hasTtop (b : Board α) : Prop :=
  ∃ ttop ∈ b.pieces, (∀ a ∈ b.pieces, a ≤ ttop) ∧ ttop ≠ ⊥

初期盤面 b が真の最大元を持つとき、すなわち、hasTop b が成り立つとき、先手必勝となります。先手必勝の証明では、先手が真の最大限のみを選んで取ることが可能であるということが一つのポイントとなります。

補題の証明 (先手キャンセル補題)

真の最大限を持つ初期盤面に絡んだ補題を証明しておきます。
真の最大元 ttop を持つ初期盤面において、先手がその ttop のみをとったとします。すると次に後手が \bot 以外のどのピース (p とします) を選んだとしても、その手で得られる盤面と、初めから先手がピース p をとったとした場合の盤面とではその形が全く同じになります。

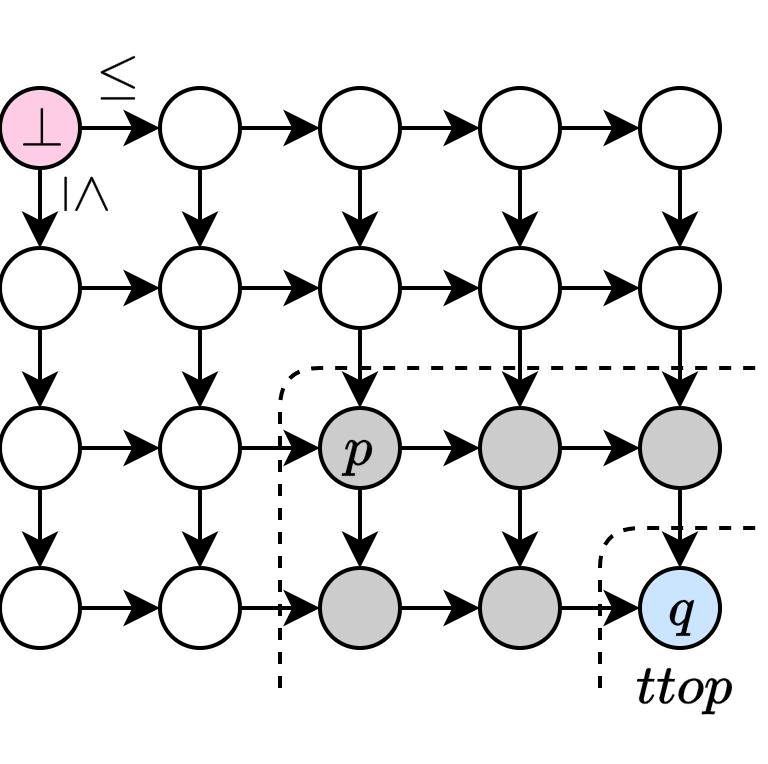
真の最大元をとる手はキャンセルできる

このことを少し一般化した形で証明しておきます。次の定理 move_move_of_le は、p \le q である場合、初めに q を取ってから次に p を取る手順と、初めから p を取る手順とでは同じ盤面が得られることを示します。つまり一手目の q を取る手はキャンセルできるという定理です。

/-- p ≤ q のとき、q を取ってから p を取る手順は、
  はじめから p を取る手順と同じ盤面を与える (一手目はキャンセルできる) -/
@[simp, grind →]
theorem Board.move_move_of_le {b b₁ b₂ : Board α} {p q : α}
  (hpq : p ≤ q) (h₁ : b.move q = some b₁) (h₂ : b₁.move p = some b₂) :
  b.move p = some b₂ := by
  simp_all
  obtain ⟨q', hq'⟩ := h₁
  obtain ⟨p', hp'⟩ := h₂
  apply Exists.intro
  · congr
    grind
  · grind

メイン定理「真の最大元を持つ盤面は勝ち盤面」の証明 (戦略盗用論法)

それでは、Chomp が先手必勝であるという定理を証明します。盤面 b_0 が真の最大元 ttop を持つとき、b_0 は勝ち盤面となります。

まず、先手が ttop を選んで取ったとします。その盤面を b_1 とすると、(排中律により) b_1 が負け盤面であるか、もしくは、b_1 が勝ち盤面であるかのどちらかが成り立ちます。

  • b_1 が負け盤面となる場合: そもそもの b_0 が勝ち盤面ということなので先手必勝
  • b_1 が勝ち盤面となる場合: 後手が必勝ということは、必勝となる手 p があるはずですが、そもそも先手がその p を初手に取っていればよいのでやはり先手必勝 (先手が p をとれるのは先に証明した補題 move_move_of_le で保障されます)

この先手が後手の手を盗用するという戦略盗用論法により、具体的な必勝手を具体的には示さないものの必勝手が存在すること自体は示すことができます。

Lean による証明は次のようになります。

theorem Board.winning_of_hasTtop {b₀ : Board α} (h : b₀.hasTtop) :
  b₀.winning := by
  obtain ⟨ttop, h₀⟩ := h -- 先手は ttop を取って move
  have h_move_ttop : ∃ b₁, b₀.move ttop = some b₁ := by
    simp_all
  obtain ⟨b₁, hb₁⟩ := h_move_ttop -- 後手は b₀ から ttop を取った盤面 b₁ を受け取る
  by_cases h₁ : b₁.losing -- b₁ が負け盤面かどうかで場合分け(排中律)
  . grind -- b₁ が負け盤面の場合: そもそも b₀ は勝ち盤面
  . grind -- b₁ が勝ち盤面の場合: 後手の手を先手が真似ればよい

by_cases タクティクで b_1 が負け盤面となる場合と勝ち盤面となる場合とに場合分けしましたが、その後の証明は grind タクティクが一行でやってくれました。grind つよい。

おまけ

勝ち盤面と負け盤面を相互再帰的に定義する

上記では、盤面 b が負け盤面であること losing b を、勝ち盤面であることの否定 ¬ winning b として定義しました。しかし、盤面が勝ち盤面であることもしくは負け盤面であるということは、次のように考えるのがより自然かもしれません。

  • 与えられた盤面が勝ち盤面であるとは、うまく一手を取ると相手に負け盤面を押し付けることができる。
  • 与えられた盤面が負け盤面であるとは、どんな一手を取っても相手に勝ち盤面を与えてしまう。

この考えに基づいて、述語 winning と losing は次のように相互再帰的に定義することができます。

mutual -- winning とlosing を相互再帰で定義

/-- 盤面 b が勝ち盤面である b.winning
  うまい一手を取ると相手に負け盤面を与えられる -/
@[grind]
def Board.winning (b : Board α) : Prop :=
  ∃ (b' : Board α) (_ : legalMove b b'), b'.losing
  decreasing_by grind

/-- 盤面 b が負け盤面である
  どんな一手をとっても相手に勝ち盤面を与えてしまう -/
@[grind]
def Board.losing (b : Board α) : Prop :=
  ∀ (b' : Board α), legalMove b b' → b'.winning
  decreasing_by grind

end

このような相互再帰による定義をした場合においても、(ある意味当然ですが) losing b と ¬ winning b は論理的には同値となります。証明は若干長くなりますが以下の通りです。

/-- losing は winning の否定と同値 -/
@[simp, grind =]
theorem Board.losing_iff_not_winning (b : Board α) :
  b.losing ↔ ¬ b.winning := by
  apply Iff.intro <;> intro h
  · rw [winning]
    push_neg
    intro b' hbb'
    have ih : b'.losing ↔ ¬ b'.winning := by -- 数学的帰納法
      have hlt : sizeOf b' < sizeOf b := by grind
      exact losing_iff_not_winning b' -- 自身を再帰で呼ぶ (hlt で整礎性を示す)
    grind
  · rw [losing]
    intro b' hbb'
    have ih : b'.losing ↔ ¬ b'.winning := by -- 数学的帰納法
      have hlt : sizeOf b' < sizeOf b := by grind
      exact losing_iff_not_winning b' -- 自身を再帰で呼ぶ (hlt で整礎性を示す)
    grind

盤面のサイズに対する数学的帰納法に対応した証明なのですが、証明の中で自分自身を再帰的に呼び出せるのは、プログラムによる証明ならではだなあという感じがして、個人的にはとても好みです。

相互再帰による定義での証明の完全版はこちらです。
https://live.lean-lang.org/#url=https%3A%2F%2Fgist.githubusercontent.com%2Frikitoro%2Fea8bf00acdb633c25987963a0eea8951%2Fraw%2FPosetChompMutual.lean

終わりに

本記事では Chomp ゲームが先手必勝であることを戦略盗用論法に基づいた証明を Lean で行いました。Lean の事始めで自然数を作ったりその性質を証明したりしてみた、その次ぐらいに取り組んでみるのにちょうどよいレベルと規模感の課題なのかなと思います。

以下、今回 Chomp の証明に取り組んでみての雑感です。

  • 証明自体よりも、証明に向けたデータ構造の定義や命題の形式化のほうが大変:
    証明にあたって必要なデータ構造の整備、例えば、盤面 Board や一手進める move 、合法手 LegalMove などどのような概念が必要かの検討や、それらをどう定義し形式化するかといったところに、証明自体よりもずっと時間も手間もかかりました。
    証明対象となる命題を形式化することも難しかったです。Lean は証明が正しいかどうかは示してくれますが、形式化した命題が本当に証明したいことを意味しているかどうかは示してくれません。
  • LLM は証明の細部はいまいちだが、証明の指針は示してくれる(場合もある):
    今回の証明の全体的な構成や、データ構造の整備は ChatGPT や Gemini などの LLM と何度もやり取りをして詰めていきました。やり取りをとおして Lean での証明を書いていくうちに、自身の理解が次第に深まっていくのがいちばんの収穫です。
    現時点においては、これらの LLM から得られた証明自体には少なからず誤りがあって、正しい証明を得るにはいろいろと試行錯誤が必要でした。また指定したにも関わらず grind タクティクを使ってくれることはなかったです (grind タクティクに対する理解はあるようですが)。今回の証明部分は結局ほぼ自身で書き直しました。
    この辺りの状況は日進月歩で、数年後もしくは数か月後にはだいぶ変わってきてるのかなとも思います。
  • grind タクティクつよい。:
    今回の証明ではひたすら grind と simp_all をたたき続けました。Mathlib で証明されている定理なども適宜使って証明してくれるようですので、すでに Mathlib でより強い定理が証明されていてそれが使われていたらどうしようと若干不安になりました(これは grind だけでなく Mathlib 使った証明全体に言えることですが)。定理を証明すること自体には問題はないですが、理解のための証明となると少し考える必要がありそうです。
    また、将来 grind タクティクの実装が変わったときに、今回通った証明が通らなくなることもあり得そうです。grind タクティクのしくみをきちんと理解し、堅牢な証明を構築する必要があるかと思われます。

Discussion