はじめに
今回はワイブル分布のパラメータ推定において、確率紙による方法1と最尤推定を用いた方法2の比較をします。
結論としては、形状パラメータ m については確率紙による推定方法1が優れ、尺度パラメータ \eta は両方法で大きな違いはありませんが、若干最尤推定による推定方法2の方が優れているという結果になります。
ただ、両方法についてワイブル分布の形状パラメータ m が 0 に近づくにつれ、 尺度パラメータ \eta の推定量は正の無限大に発散するため、推定精度は低下します。
最尤推定による推定を改良した場合は両推定方法に勝ります。詳細はこちらの記事をご覧ください。
概要
前置き
X を形状パラメータ m 、尺度パラメータ \eta のワイブル分布 W(m,\eta) に従う確率変数とすると、
確率密度関数 f(x) 、累積分布関数 F(x) は
\begin{aligned}
f(x)&=\dfrac{m}{\eta}\left(\dfrac{x}{\eta} \right)^{m-1}
\exp\left\{-\left(\dfrac{x}{\eta} \right)^{m} \right\} \\
F(x)&=1-\exp\left\{-\left(\dfrac{x}{\eta} \right)^{m} \right\} \\
\end{aligned}
と表されます。
X \sim W(m,\eta) から互いに独立に得られた n 個の観測値を小さい順に x_{(1)},\ ...\ ,x_{(n)} とします。
方法1 確率紙による推定
X の累積分布関数 F(x) と観測値 x について y=\ln{[-\ln{\{1-F(x)\}}]} と \ln{x} は直線になります。
これを利用し、観測値から \ln{x},y をプロットし、最小二乗法により未知パラメータを求める方法です。
得られた観測値 x_{(i)} に対し、y_{i} = \ln{\left[- \ln{\{ 1-F(x_{(i)})\}} \right]} (i=1, ...\ ,n) とすると、
m,\eta の推定値 \hat{m}_{1}, \hat{\eta}_{1} は
\left\{\begin{aligned}
\hat{m}_1 &= \dfrac{\sum_{i=1}^{n}(\ln{x_{(i)}} - \overline{\ln{x}})(y_{i}-\bar{y})}
{\sum_{i=1}^{n}(\ln{x_{(i)}}- \overline{\ln{x}})^{2}} \\
\hat{\eta}_1 &= \exp{\left[ -\dfrac{\bar{y}-\hat{m}_1\overline{\ln{x}}}{\hat{m}_1} \right]}
\end{aligned}\right.
\left( \begin{aligned}
\bar{y}= \dfrac{1}{n}\sum_{i=1}^{n} y_{i}\ ,
\ \overline{\ln{x}} =\dfrac{1}{n} \sum_{i=1}^{n} \ln{x_{(i)}}
\end{aligned} \right)
と表せます。詳細は [2] をご覧ください。
方法2 最尤推定による推定
X \sim W(m,\eta) から互いに独立に得られた n 個の観測値を x_{1},\ ...\ ,x_{n} とすると、
m の最尤推定量 \hat{m}_{2} は
\begin{aligned}
g(m)
&= \dfrac{1}{m} + \dfrac{1}{n}\sum_{i=1}^{n}\ln{x_{i}}
-\dfrac{\sum_{i=1}^{n} x_{i}^{m} \ln{x_{i}}}{\sum_{i=1}^{n} x_{i}^{m}} \\
&=0
\end{aligned}
を満たす m となります。
ニュートン法により、以下の漸化式を反復計算することにより \hat{m}_{2} を計算します。
\begin{aligned}
m_{k+1}= m_{k}- \dfrac{g(m_{k})}{g'(m_{k})}
\end{aligned}
\eta の最尤推定量 \hat{\eta}_{2} は
\begin{aligned}
\hat{\eta}_{2} &= \sqrt[\footnotesize \hat{m}_{2}]{\dfrac{1}{n} \sum_{i=1}^{n} x_{i}^{\hat{m}_{2}}}
\end{aligned}
と表せます。詳細は [3] をご覧ください。
欠点として、m が大きく、n が小さいほど、m の最尤推定の計算が発散しやすくなります。参考程度に m=5,n=4 で1万回に1回程度、m=5,n=5 の場合で10万回に1回程度発生します。m=5,n=6 の場合では全く発生しません。観測値がすべて近しい値の場合は最尤推定量 \hat{m}_{2} の値が大きくなり、発散しやすい傾向にあります。
比較方法
方法の比較は以下の手順で実施します。
- 逆関数法によりワイブル分布に従う乱数を生成 *詳細は[1]をご覧ください
- 得られた乱数(観測値)から、各方法において未知パラメータ m,\eta を推定
- 上記の試行を10000回繰り返し、各方法について推定値の平均値と不偏分散を計算
- 平均値の相対誤差と、相対化した分散(不偏分散を真値の2乗で割った値)をグラフ化し比較
結果
-
m の推定:確率紙による推定方法1よい。観測値の数が約50以上の場合は、最尤推定による推定方法2がよい。
-
\eta の推定:最尤推定による推定方法2がよい。欠点として、両者ともに m が小さい場合は、\eta の推定値は正の無限大に発散するため、観測値の数を大きくする必要あり。
Python ソースコード
こちらをご覧ください。
[1] 逆関数法によるワイブル分布に従う乱数の生成
確率密度関数 f(x)、累積分布関数 F(x) で表される分布に従う乱数の生成方法は、標準一様分布 U(0,1) から得られる乱数 u を累積分布関数の逆変換 ( F^{-1} ) をすることにより可能となります。
ワイブル分布の累積分布関数 F(x) の逆関数を求めると、
\begin{aligned}
F(x)&=1-\exp\left\{-\left(\dfrac{x}{\eta} \right)^{m} \right\} \\
1-F(x)&=\exp\left\{-\left(\dfrac{x}{\eta} \right)^{m} \right\} \\
\ln{(1-F(x))} &= -\left( \dfrac{x}{\eta} \right)^{m}\\
x^{m} &= -\eta^{m}\ln{(1-F(x))}\\
x &=\eta\sqrt[\footnotesize m]{-\ln{(1-F(x))}}
\end{aligned}
よって、累積分布関数 F(x) の逆関数 F^{-1}(x) は
\begin{aligned}
F^{-1}(x)&=\eta\sqrt[\footnotesize m]{-\ln{(1-x)}}
\end{aligned}
となります。
以上より、U(0,1) に従う一様乱数 u を生成後、 x=F^{-1}(u) と変換すれば、ワイブル分布 W(m,\eta) に従う乱数を生成することができます。
[2] 方法1:確率紙によるパラメータ推定
まず、\ln{\ln{\dfrac{1}{1-F(x)}}} を計算すると、
\begin{aligned}
\ln{\ln{\dfrac{1}{1-F(x)}}} &= \ln{[-\ln{\{1-F(x)\}}]} \\
&= \ln{\left(\dfrac{x}{\eta} \right)^m} \\
&= m( \ln{x} - \ln{\eta} )
\end{aligned}
と表すことができます。 y=\ln{[-\ln{\{1-F(x)\}}]} とすると y と \ln{x} は線形の関係にあることが分かります。
よって、X \sim W(m,\eta) から互いに独立に得られた n 個の観測値を小さい順に並べたものを x_{(1)},\ ...\ ,x_{(n)} とし、 y_{i} = \ln{\left[- \ln{\{ 1-F(x_{(i)})\}} \right]} とした場合、\ln{x_{(i)}} と y_{i} をプロットすると直線になります。累積分布関数 F(x_{(i)}) の推定については Benard の近似式を使用します。
\begin{aligned}
F(x_{(i)}) \approx \dfrac{i-0.3}{n+0.4}
\end{aligned}
累積分布関数の推定に関してはこちらの記事をご覧ください。
\ln{x_{(i)}} と y_{i} について y=a \ln{x} + b と直線近似することを考えます。
最小二乗法により、係数 a,b については
\left\{\begin{aligned}
a&=\dfrac{\sum_{i=1}^{n}(\ln{x_{(i)}} - \overline{\ln{x}})(y_{i}-\bar{y})}
{\sum_{i=1}^{n}(\ln{x_{(i)}}- \overline{\ln{x}})^{2}} \\
b&= \bar{y} - a\ \overline{\ln{x}}
\end{aligned}\right.
\left( \begin{aligned}
\bar{y}= \dfrac{1}{n}\sum_{i=1}^{n} y_{i}\ ,
\ \overline{\ln{x}} =\dfrac{1}{n} \sum_{i=1}^{n} \ln{x_{(i)}}
\end{aligned} \right)
で表されます。 a=m, b=-m\ln{\eta} から、確率紙による m,\eta の推定量 \hat{m}_{1},\hat{\eta}_{1} は
\left\{\begin{aligned}
\hat{m}_1 &= \dfrac{\sum_{i=1}^{n}(\ln{x_{(i)}} - \overline{\ln{x}})(y_{i}-\bar{y})}
{\sum_{i=1}^{n}(\ln{x_{(i)}}- \overline{\ln{x}})^{2}} \\
\hat{\eta}_1 &= \exp{\left[ -\dfrac{\bar{y}-\hat{m}_1\overline{\ln{x}}}{\hat{m}_1} \right]}
\end{aligned}\right.
となります。
[3] 方法2:ワイブル分布の最尤推定によるパラメータ推定
ワイブル分布の尤度関数を L(m,\eta) とすると、観測値を x_{1},\ ...\ ,x_{n} として、
\begin{aligned}
L(m,\eta)
&=\prod_{i=1}^{n}\dfrac{m}{\eta}\left( \dfrac{x_{i}}{\eta} \right) ^{m-1}
\exp{\left[- \left( \dfrac{x_{i}}{\eta} \right)^{m} \right]}\\
&=\left( \dfrac{m}{\eta} \right)^{n}
\left\{ \prod_{i=1}^{n}\left( \dfrac{x_{i}}{\eta} \right) ^{m-1} \right\}
\exp{\left[ -\sum_{i=1}^{n}\left( \dfrac{x_{i}}{\eta}\right)^{m} \right]}
\end{aligned}
対数尤度関数については
\begin{aligned}
\ln{L(m,\eta)}
&=n(\ln{m} -\ln{\eta}) + (m-1)\sum_{i=1}^{n}(\ln{x_{i}}-\ln{\eta})
-\sum_{i=1}^{n}\left( \dfrac{x_{i}}{\eta}\right)^{m} \\
\end{aligned}
対数尤度関数が最大となる m,\eta を求めると、以下の2式が成り立ちます。
\left\{\begin{aligned}
\dfrac{\partial}{\partial m}\ln{L(m,\eta)} = 0 \\
\dfrac{\partial}{\partial \eta}\ln{L(m,\eta)} = 0 \\
\end{aligned}\right.
\eta については
\begin{aligned}
\dfrac{\partial}{\partial \eta}\ln{L(m,\eta)}
&=-\dfrac{n}{\eta} + (m-1) \sum_{i=1}^{n}\left( -\dfrac{1}{\eta} \right)
-\sum_{i=1}^{n}\left( -m\dfrac{x_{i}^{m}}{\eta^{m+1}}\right) \\
&=-\dfrac{mn}{\eta}
+\dfrac{m}{\eta}\sum_{i=1}^{n}\left( \dfrac{x_{i}}{\eta}\right)^{m} \\
&=\dfrac{m}{\eta} \left(-n + \sum_{i=1}^{n}\left( \dfrac{x_{i}}{\eta}\right)^{m} \right) =0\\
\end{aligned}
よって、
\begin{aligned}
n &=\sum_{i=1}^{n}\left( \dfrac{x_{i}}{\eta}\right)^{m}\\
\eta^{m} &=\dfrac{1}{n} \sum_{i=1}^{n} x_{i}^{m} \\
\eta &= \sqrt[\footnotesize m]{\dfrac{1}{n} \sum_{i=1}^{n} x_{i}^{m}}
\end{aligned}
m については
\begin{aligned}
\dfrac{\partial}{\partial m}\ln{L(m,\eta)}
&=\dfrac{n}{m} + \sum_{i=1}^{n}(\ln{x_{i}}-\ln{\eta})
-\sum_{i=1}^{n} \left( \dfrac{x_{i}}{\eta}\right)^{m} (\ln{x_{i}} -\ln{\eta})\\
&=\dfrac{n}{m} + \sum_{i=1}^{n}\ln{x_{i}}-n\ln{\eta}
+\ln{\eta} \sum_{i=1}^{n}\left( \dfrac{x_{i}}{\eta}\right)^{m}
-\sum_{i=1}^{n} \left( \dfrac{x_{i}}{\eta}\right)^{m} \ln{x_{i}}
\\
&=\dfrac{n}{m} + \sum_{i=1}^{n}\ln{x_{i}}
-\dfrac{1}{\eta^{m}}\sum_{i=1}^{n} x_{i}^{m} \ln{x_{i}}
\left(\because n = \sum_{i=1}^{n}\left( \dfrac{x_{i}}{\eta}\right)^{m} \right)\\
&=\dfrac{n}{m} + \sum_{i=1}^{n}\ln{x_{i}}
-n\dfrac{\sum_{i=1}^{n} x_{i}^{m} \ln{x_{i}}}{\sum_{i=1}^{n} x_{i}^{m}} \\
&=n\left( \dfrac{1}{m} + \dfrac{1}{n}\sum_{i=1}^{n}\ln{x_{i}}
-\dfrac{\sum_{i=1}^{n} x_{i}^{m} \ln{x_{i}}}{\sum_{i=1}^{n} x_{i}^{m}} \right) =0 \\
\end{aligned}
となります。 m については解くことができないため、ニュートン法を使用します。
\begin{aligned}
g(m)= \dfrac{1}{m} + \dfrac{1}{n}\sum_{i=1}^{n}\ln{x_{i}}
-\dfrac{\sum_{i=1}^{n} x_{i}^{m} \ln{x_{i}}}{\sum_{i=1}^{n} x_{i}^{m}}
\end{aligned}
とすると
\begin{aligned}
g'(m)
&= -\dfrac{1}{m^{2}} - \dfrac{\sum_{i=1}^{n} x_{i}^{m} (\ln{x_{i}})^{2}}{\sum_{i=1}^{n} x_{i}^{m}}
-\sum_{i=1}^{n} x_{i}^{m} \ln{x_{i}}
\left( - \dfrac{\sum_{i=1}^{n} x_{i}^{m} \ln{x_{i}}}
{ \left( \sum_{i=1}^{n} x_{i}^{m} \right)^{2} } \right) \\
&= -\dfrac{1}{m^{2}} - \dfrac{\sum_{i=1}^{n} x_{i}^{m} (\ln{x_{i}})^{2}}{\sum_{i=1}^{n} x_{i}^{m}}
+ \left( \dfrac{\sum_{i=1}^{n} x_{i}^{m} \ln{x_{i}}}
{ \sum_{i=1}^{n} x_{i}^{m} } \right)^{2} \\
\end{aligned}
となります。
初期値 m_{0} を方法1で推定した \hat{m}_{1} として、以下の漸化式を反復計算することで、方法2の m の最尤推定量 \hat{m}_{2} を求めます。
\begin{aligned}
m_{k+1}= m_{k}- \dfrac{g(m_{k})}{g'(m_{k})}
\end{aligned}
\eta の最尤推定量 \hat{\eta}_{2} は \hat{m}_{2} を使用して、
\begin{aligned}
\hat{\eta}_{2} &= \sqrt[\footnotesize \hat{m}_{2}]{\dfrac{1}{n} \sum_{i=1}^{n} x_{i}^{\hat{m}_{2}}}
\end{aligned}
より求めます。
簡易シミュレーションによる比較結果
前置き
本項では、pythonを使用したシミュレーションにより以下の2方法によるパラメータ推定の精度を比較します。
- 方法1:確率紙による推定
- 方法2:最尤推定量による推定
方法の比較は以下の手順で実施します。
- 逆関数法によりワイブル分布に従う乱数を生成
- 得られた乱数(観測値)から、各方法において未知パラメータ m,\eta を推定
- 上記の試行を10000回繰り返し、各方法について推定値の平均値と不偏分散を計算
- 平均値の相対誤差と、相対化した分散(不偏分散を真値の2乗で割った値)をグラフ化し比較
推定精度の評価には”平均値と真値の相対誤差”と”不偏分散を真値の二乗で割った、相対化した分散”を使用します。
具体的には、未知パラメータの真値を \theta、i 回目の推定値を \hat{\theta}_{i}、推定値の平均を \hat{\theta}_{mean}、不偏分散を S^{2}_{\hat{\theta}}、試行回数を N として、
- 推定値の平均値の相対誤差 =\dfrac{\hat{\theta}_{mean}-\theta}{\theta}
- 相対化した分散 =\dfrac{S^{2}_{\hat{\theta}}}{\theta^{2}}
\begin{aligned}
\hat{\theta}_{mean} = \dfrac{1}{N}\sum_{i=1}^{N} \hat{\theta}_{i} ,\
S^{2}_{\hat{\theta}} = \dfrac{1}{N-1}\sum_{i=1}^{N} (\hat{\theta}_{i} - \hat{\theta}_{mean})^{2}
\end{aligned}
と表せます。
結果
最初に、m を 0.1 から 5 まで変化させたときの推定値の平均の相対誤差、相対化した分散をグラフ化したものを以下に示します。
条件:m=0.1,\ ...\ ,5.0 、\eta=100 、乱数の数 n=10 、試行回数 N=10000
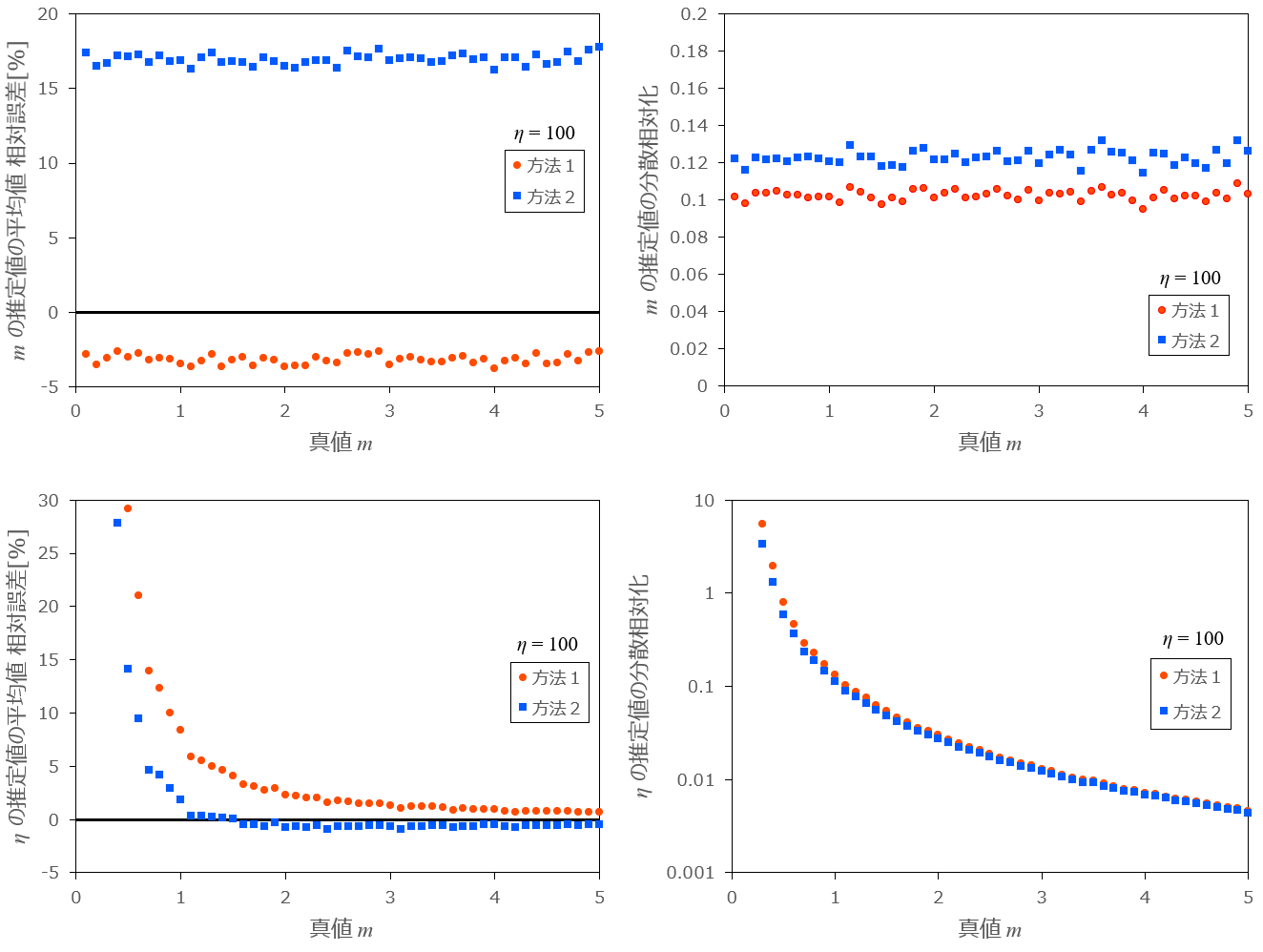
図1-1:m を変化させたときの各方法の相対誤差と分散の推移
m が小さい場合は \eta の推定値は非常に大きくなります。m =0.1,\ ...\ ,0.5 の場合は別途以下のグラフに示します。
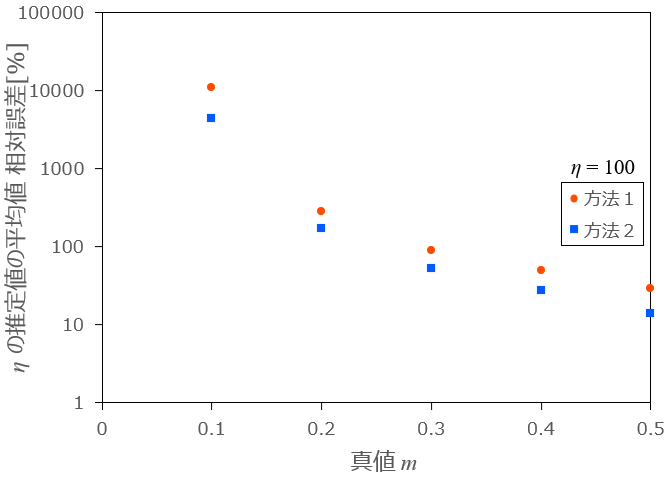
図1-2:m を変化させたときの各方法の相対誤差と分散の推移 (0 \lt m \lt 0.5)
次に、\eta を 1 から 10000 まで変化させたときの推定値の平均の相対誤差、相対化した分散をグラフ化したものを以下に示します。
条件:m=0.5 、\eta=1,2,5,10,\ ...\ ,10000 、乱数の数 n=10 、試行回数 N=10000
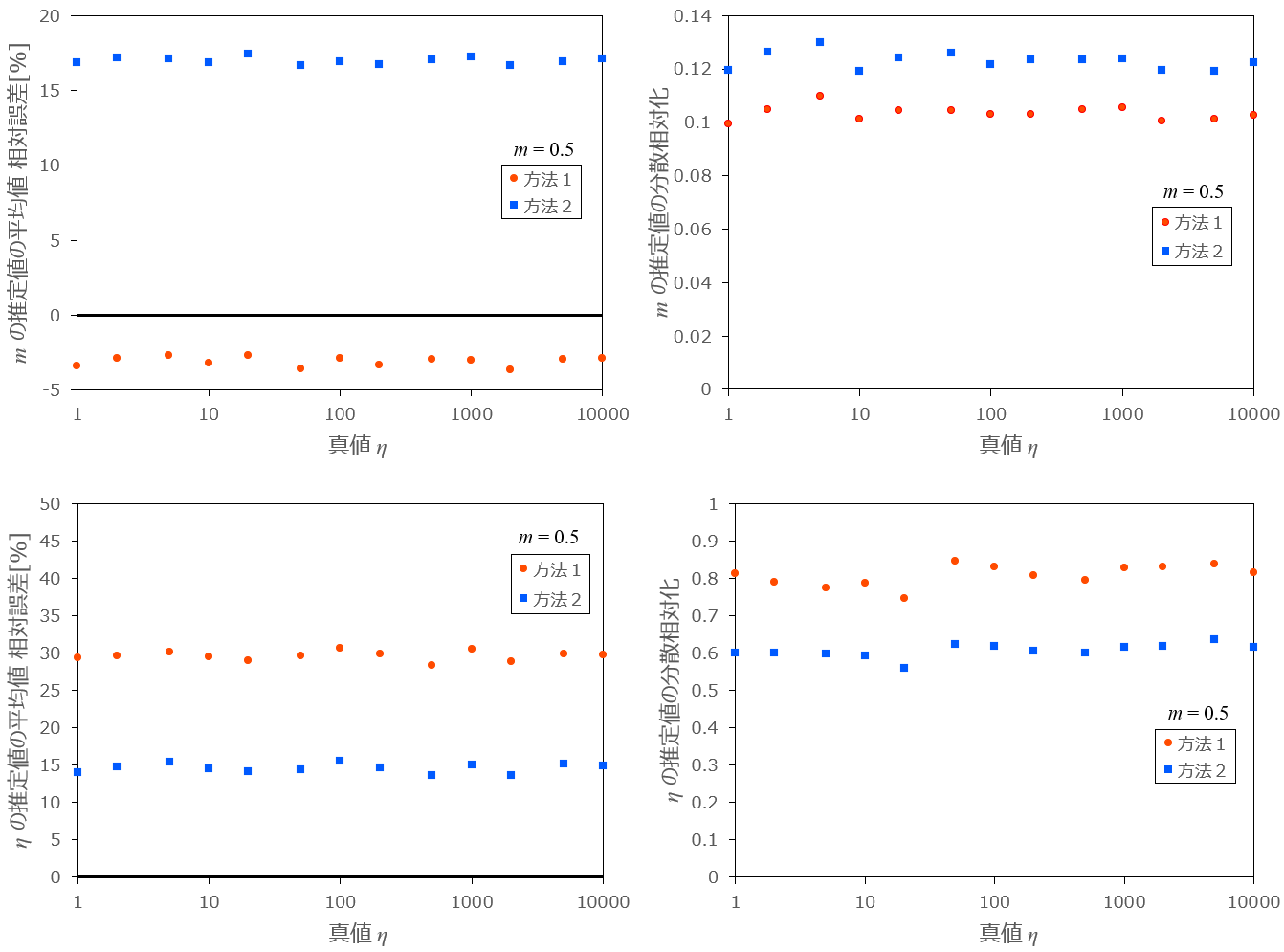
図2:\eta を変化させたときの各方法の相対誤差と分散の推移
最後に、乱数の数 n を 5 から 10000 まで変化させたときの推定値の平均の相対誤差、相対化した分散をグラフ化したものを以下に示します。
条件:m=0.5 、\eta=100 、乱数の数 n=5,10,20,50,\ ...\ ,10000 、試行回数 N=10000
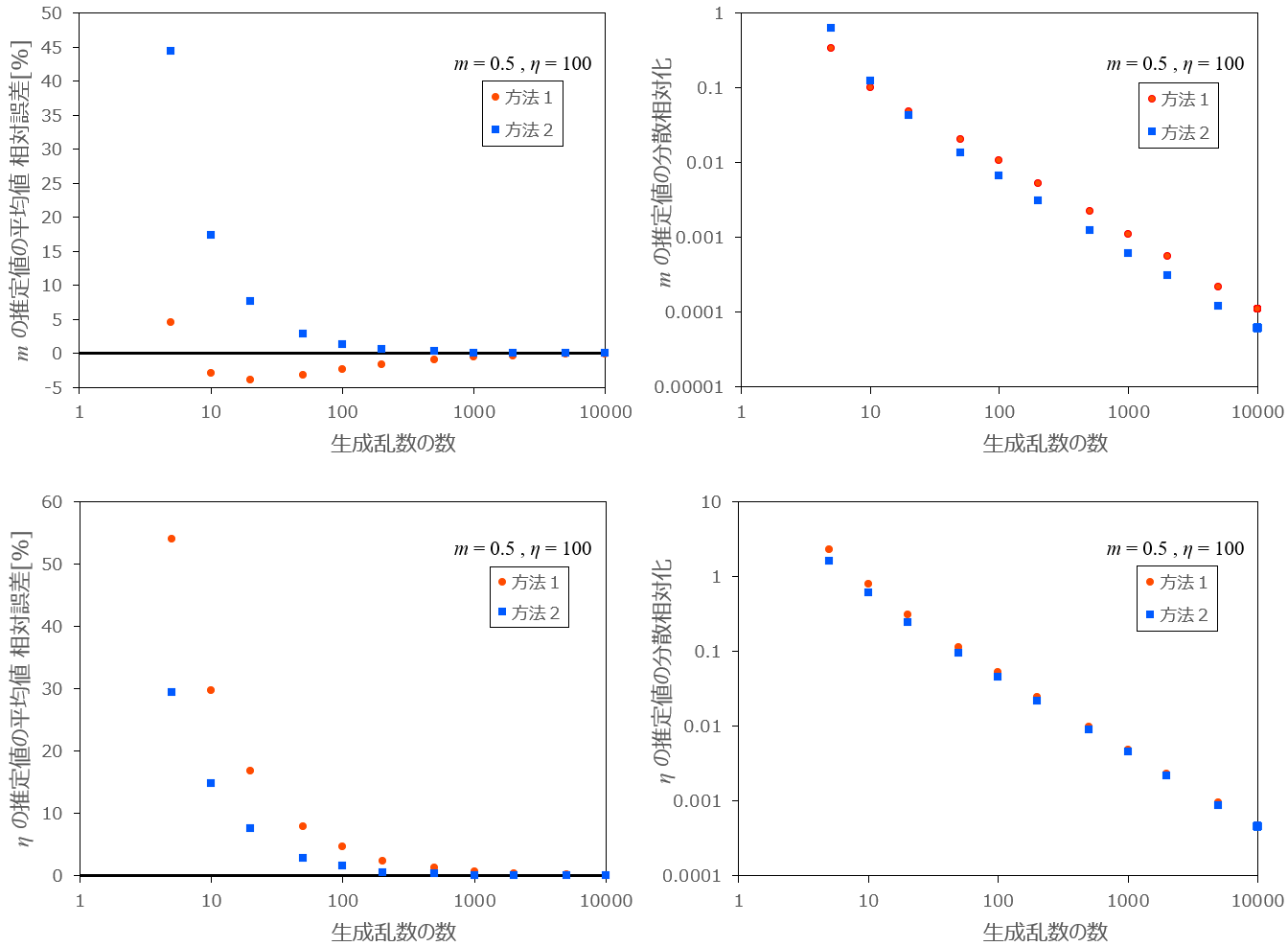
図3:生成乱数の数 n を変化させたときの各方法の相対誤差と分散の推移
まとめ
以上の結果から、m の推定については確率紙による推定方法1が勝りますが、乱数の生成数 = 観測値の数が約50以上の場合は、最尤推定による推定方法2が優れます。乱数の生成数 n が小さい場合は相対誤差が大きいことから、両方法の推定量は m の不偏推定量ではないことが分かります。n が大きい場合は、相対誤差、分散ともに0に近づくので、一致推定量であると判断できます。
\eta による推定は乱数の生成数に関係なく、最尤推定による推定方法2が優れていますが、両者ともに m が小さい場合は、\eta の推定値は正の無限大に発散するため、推定値の分散が大きくなり、観測値の数=サンプルサイズは大きくする必要があります。
Python ソースコード
こちらをご覧ください。




Discussion