【ワイブル分布】 未知パラメータ推定方法の改良
はじめに
今回はワイブル分布のパラメータ推定において最尤推定量による方法、確率紙による推定方法を改良した方法について説明します。
確率紙による推定方法、最尤推定による推定方法には2点問題点があります。
1点目は形状パラメータ
2点目は尺度パラメータ
今回は、上記2点を改善した推定方法を発見しましたので、解説します。
概要
前置き
確率密度関数
と表されます。
形状パラメータ m の改良版推定量
と表せます。
ここで、
を満たします。解析的に解くことができないため、ニュートン法により、以下の漸化式を反復計算することにより
詳細は [1] をご覧ください
尺度パラメータ η の改良版推定量
と表せます。ガンマ関数は発散しやすいため、
と表せます。詳細は [2] をご覧ください。
各推定量の比較方法
従来と改良版の以下3方法による推定の精度を比較します。
- 方法1:確率紙を用いた推定
\hat{m}_{1} \hat{\eta}_{1} - 方法2:最尤推定を用いた推定
\hat{m}_{2}, \hat{\eta}_{2} - 方法3:改良した最尤推定を用いた推定
\hat{m}_{3}, \hat{\eta}_{3}
方法の比較は以下の手順で実施します。
- 逆関数法によりワイブル分布に従う乱数を生成
- 得られた乱数(観測値)から、各方法において未知パラメータ
m,\eta - 上記の試行を100000回繰り返し、各方法について推定値の平均値と不偏分散を計算
- 平均値の相対誤差と、相対化した分散(不偏分散を真値の2乗で割った値)をグラフ化し比較
方法1、方法2の具体的な計算方法、ワイブル分布に従う乱数の生成についてはこちらの記事をご覧ください。
結果
-
m,\eta -
m \rightarrow -
\eta m n
もともと
詳細は [3] をご覧ください
Python ソースコード
今回の簡易シミュレーションで使用した Python のソースコードは [4] をご覧ください。
[1] 形状パラメータ m の改良版推定量の解説
まず、
- ワイブル分布に従う乱数を生成
- 得られた乱数(観測値)から、最尤推定により
m - 上記の試行を100000回繰り返し、上で計算した推定値の平均をとり、期待値とする
-
\hat{m}_{2} m -
\hat{m}_{2} \eta -
\hat{m}_{2} - 3.で直線近似した傾き
a_{m} b_{m} m
1.については、横軸に真値
条件:
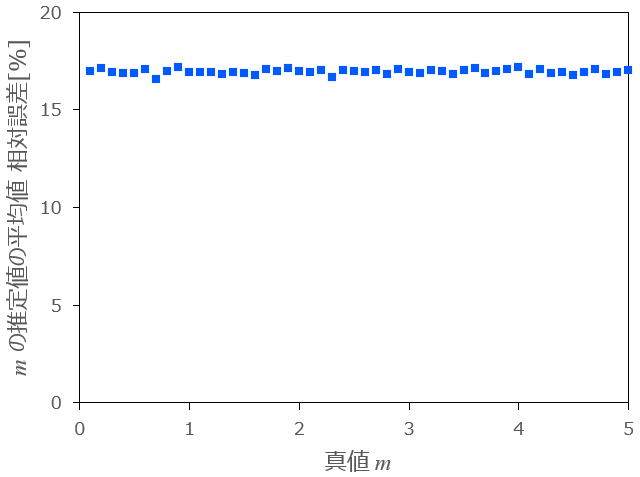
図1:
上図1より、相対誤差は
2.については、横軸に真値
条件:
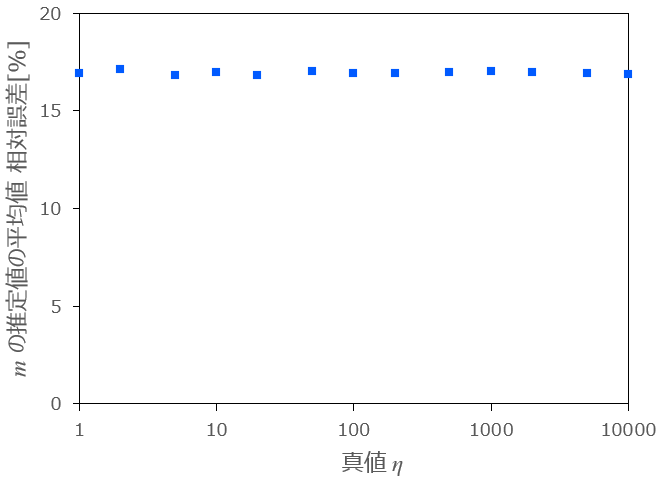
図2:
上図2より、相対誤差は
3.については、横軸に生成乱数の数
条件:
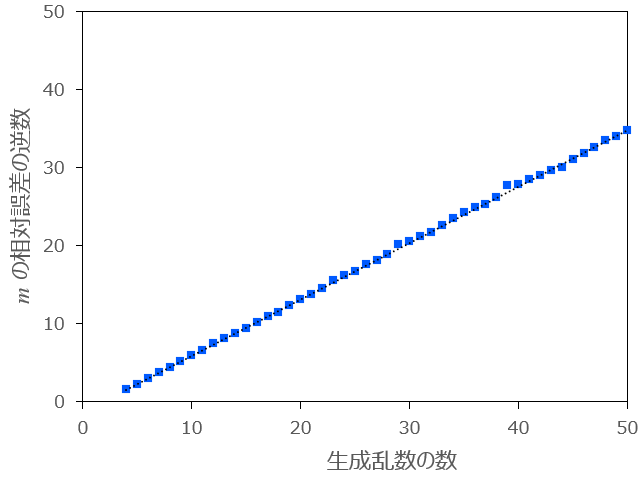
図3-1:生成乱数の数
上図3ー1より、相対誤差の逆数と乱数の数をプロットすると非常な綺麗な直線となります。
条件:
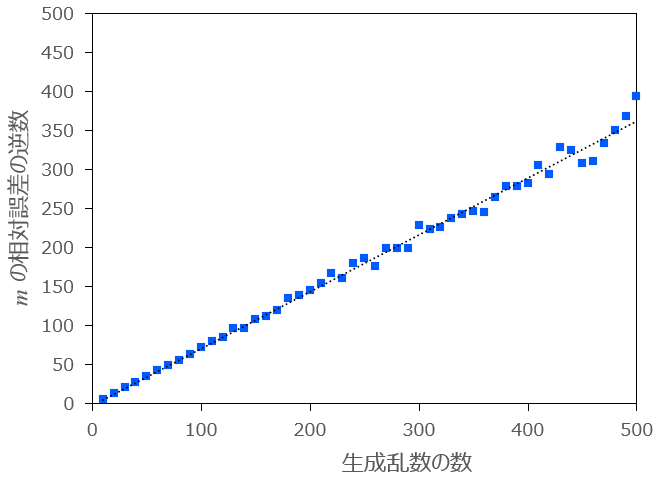
図3-2:生成乱数の数
図3-2から、
4.について、相対誤差と乱数の数
このとき、
横軸に真値
条件:
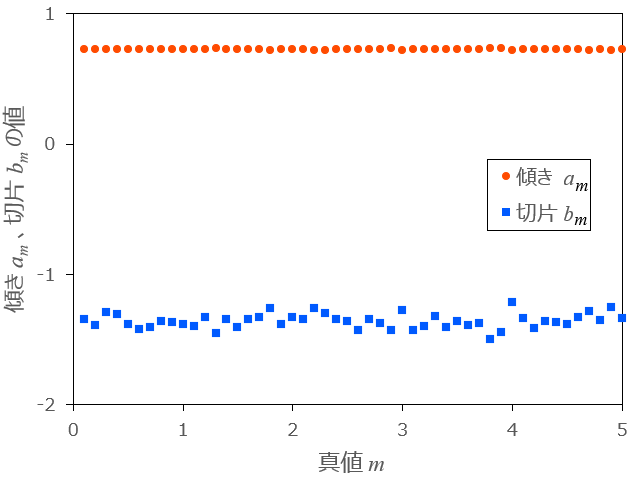
図4:
以上より、相対誤差の逆数が
これを、式変形することにより、
と表すことができます。したがって、
詳細についてはこちらの補足記事をご覧ください。
"
[2] 尺度パラメータ η の改良版推定量の解説
まず、
縦軸に
条件:
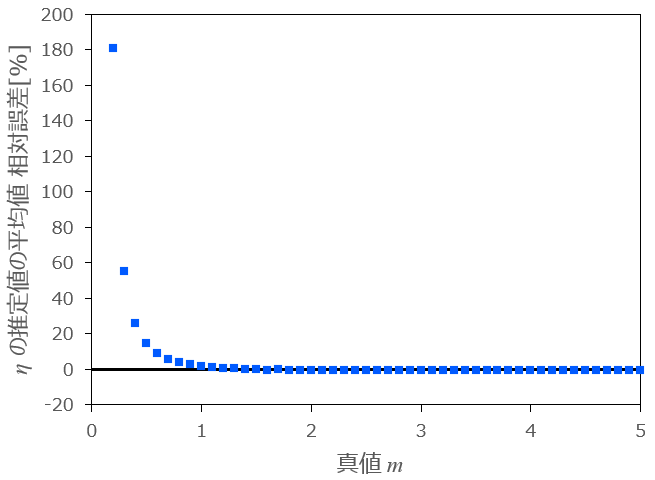
図5:
次に、推定値
縦軸に
条件:
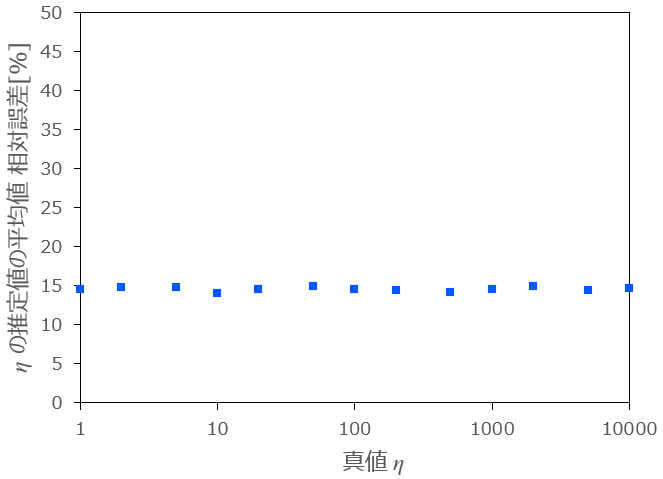
図6:
上図6より、相対誤差は
そこで、
m が既知の場合の η の最尤推定量の期待値
形状パラメータの真値
まず、
となり、
次に、
と表せます。最尤推定量
となります。以上より、補正係数を
ガンマ関数は値が大きくなりやすいため、
m が未知の場合の η の推定と各方法の比較
形状パラメータ
-
\hat{\eta}_{22} \rightarrow\hat{m}_{2} C_{\eta} \rightarrow\hat{m}_{2} -
\hat{\eta}_{33} \rightarrow\hat{m}_{3} C_{\eta} \rightarrow\hat{m}_{3} -
\hat{\eta}_{23} \rightarrow\hat{m}_{2} C_{\eta} \rightarrow\hat{m}_{3} -
\hat{\eta}_{32} \rightarrow\hat{m}_{3} C_{\eta} \rightarrow\hat{m}_{2}
上の4通りについて推定の精度を比較します。比較は以下の手順で実施します。
- ワイブル分布に従う乱数を生成
- 得られた乱数(観測値)から、4方法において尺度パラメータ
\eta - 上記の試行を100000回繰り返し、各推定値の平均値と不偏分散を計算
- 平均値の相対誤差と、相対化した分散(不偏分散を真値
\eta
以下、上記の4通りについて、推定値の平均 (
最初に、
条件:
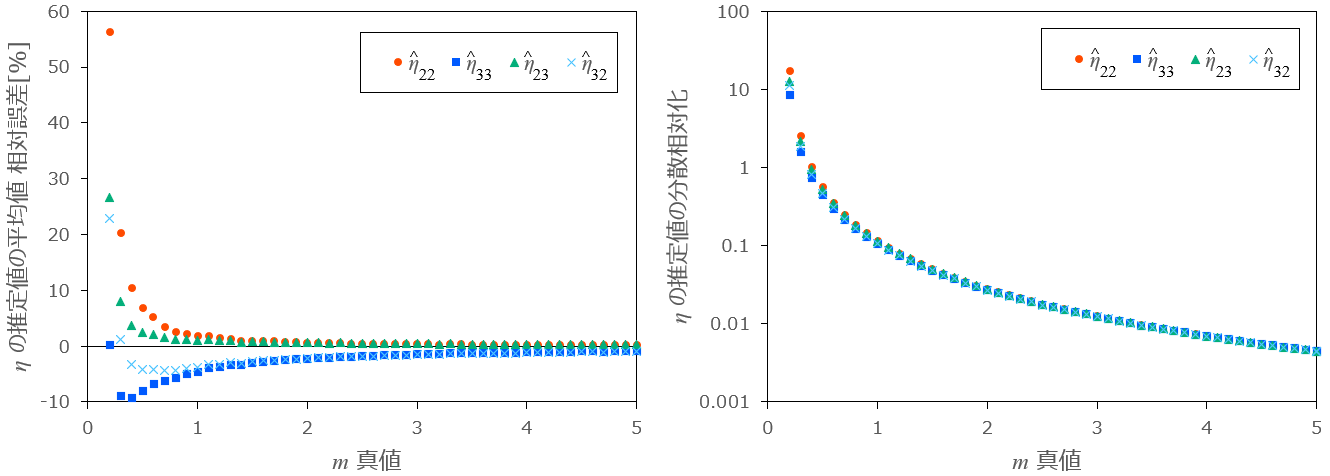
図7:
次に、
条件:
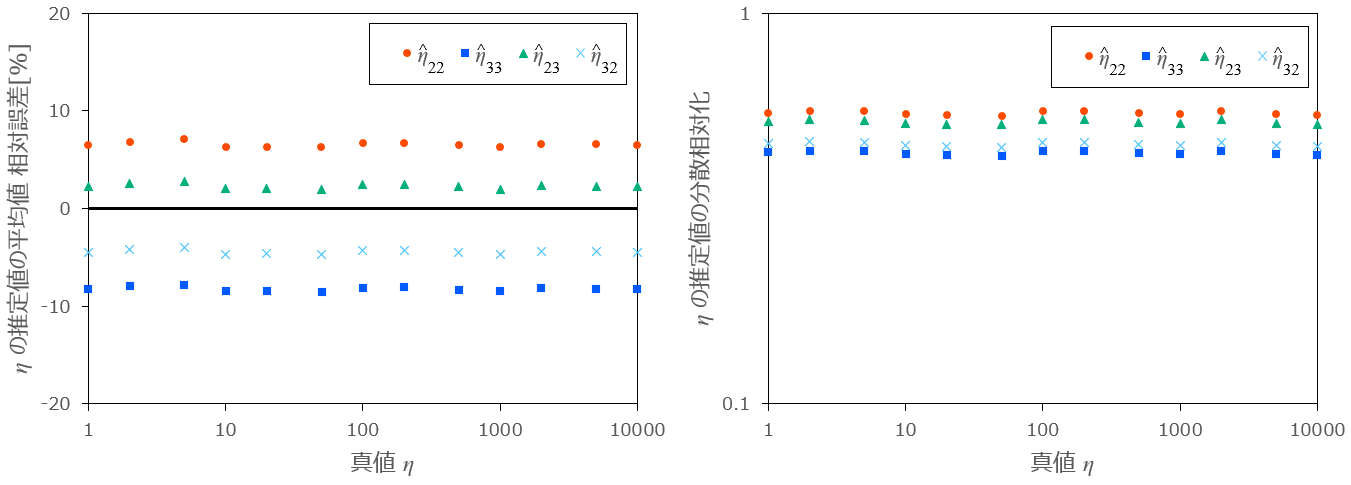
図8:
最後に、生成乱数の数
条件:
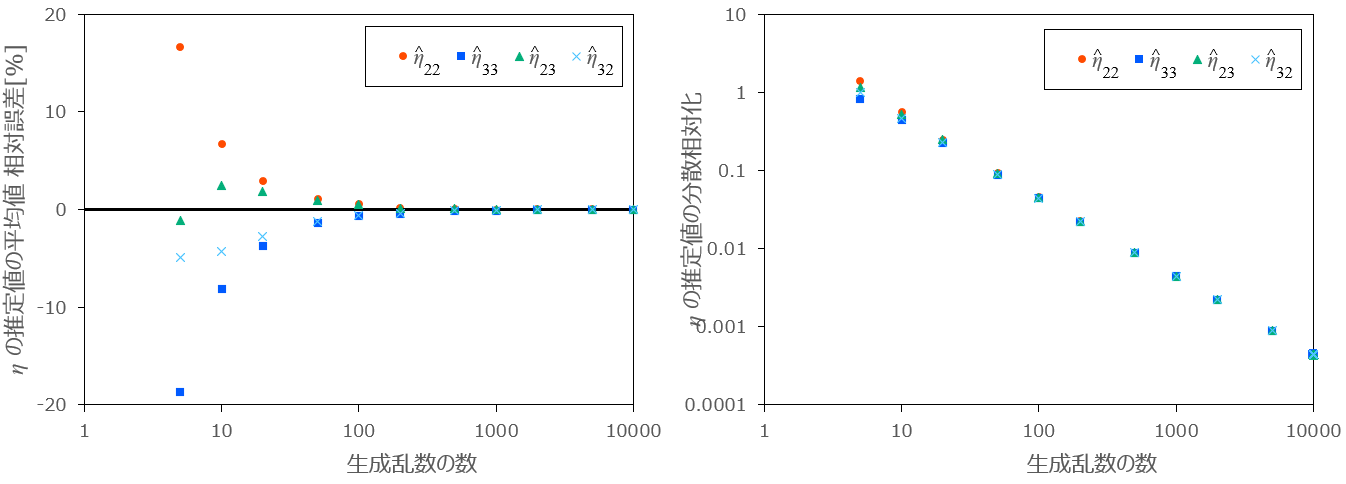
図9:生成乱数の数
以上より、
[3] 各推定量の比較結果
前置き
本項では、pythonを使用したシミュレーションにより、以下の3方法による推定量の推定精度を比較します。
- 方法1:確率紙を用いた推定量
\hat{m}_{1} \hat{\eta}_{1} - 方法2:最尤推定量を用いた推定
\hat{m}_{2}, \hat{\eta}_{2} - 方法3:改良した推定
\hat{m}_{3}, \hat{\eta}_{3}
比較方法は以下の手順で実施します。
- 逆関数法によりワイブル分布に従う乱数を生成
- 得られた乱数(観測値)から、各方法において未知パラメータ
m,\eta - 上記の試行を100000回繰り返し、各推定値の平均値と不偏分散を計算
- 平均値の相対誤差と、相対化した分散(不偏分散を真値の2乗で割った値)をグラフ化
推定値の評価には平均値と真値の相対誤差と分散を真値の二乗で割った、相対化した分散を使用します。
未知パラメータの真値を
- 推定値の相対誤差
=\dfrac{\hat{\theta}_{mean}-\theta}{\theta} - 相対化した分散
=\dfrac{S^{2}_{\hat{\theta}}}{\theta^{2}}
と表せます。
結果のグラフ
最初に、
条件:
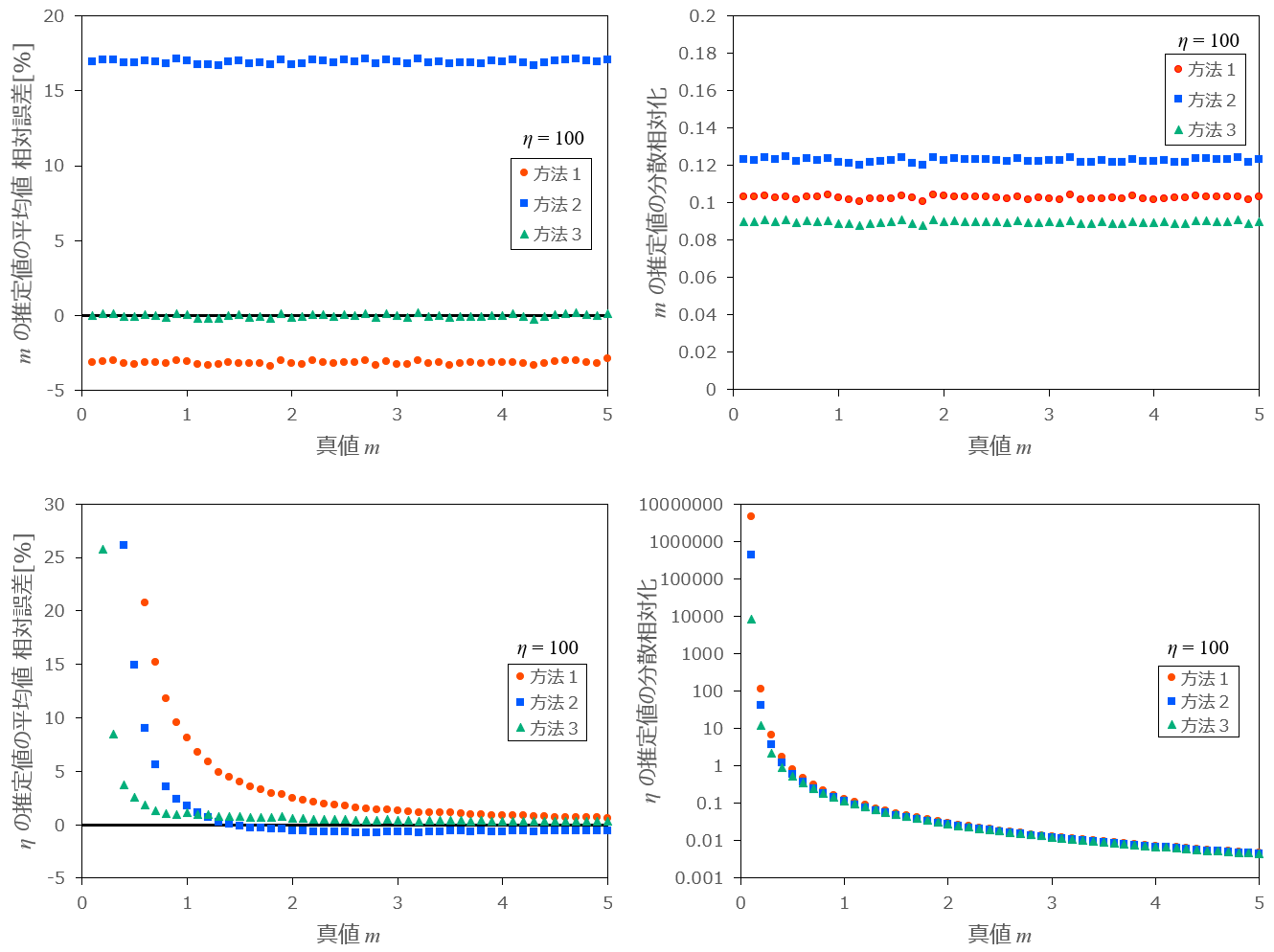
図10-1:
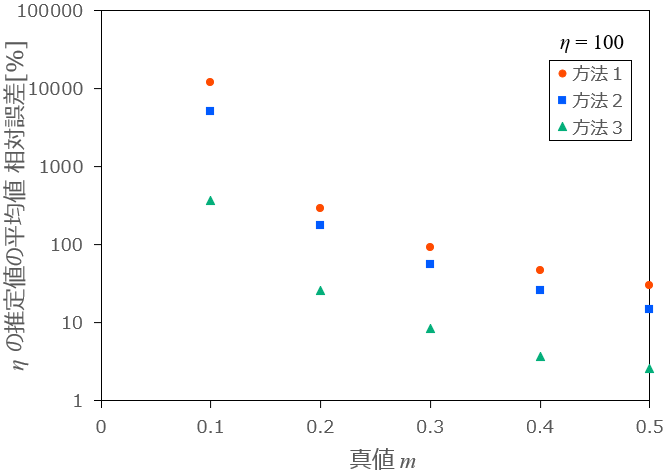
図10-2:
次に、
条件:
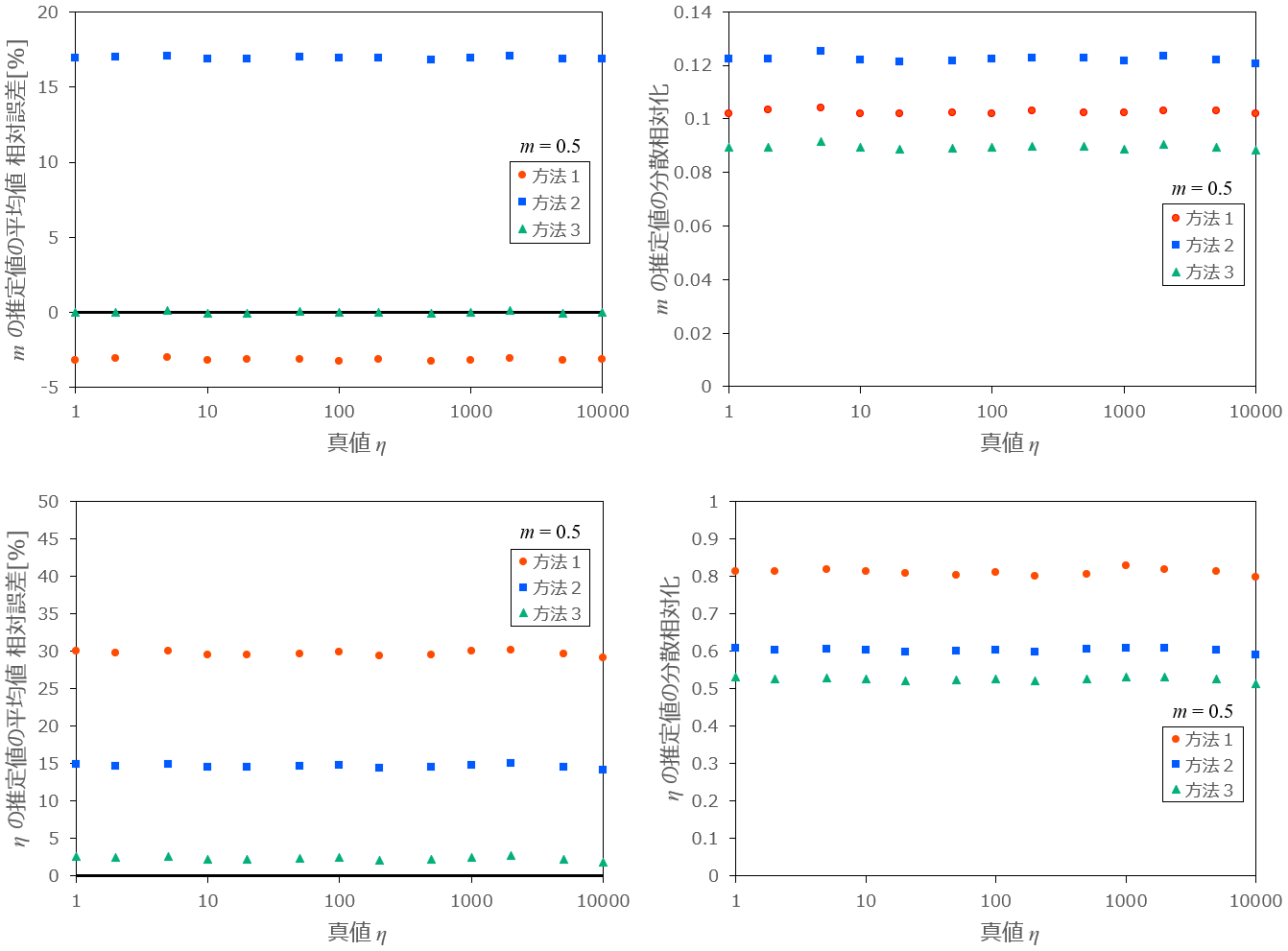
図11:
最後に、生成乱数の数
条件:
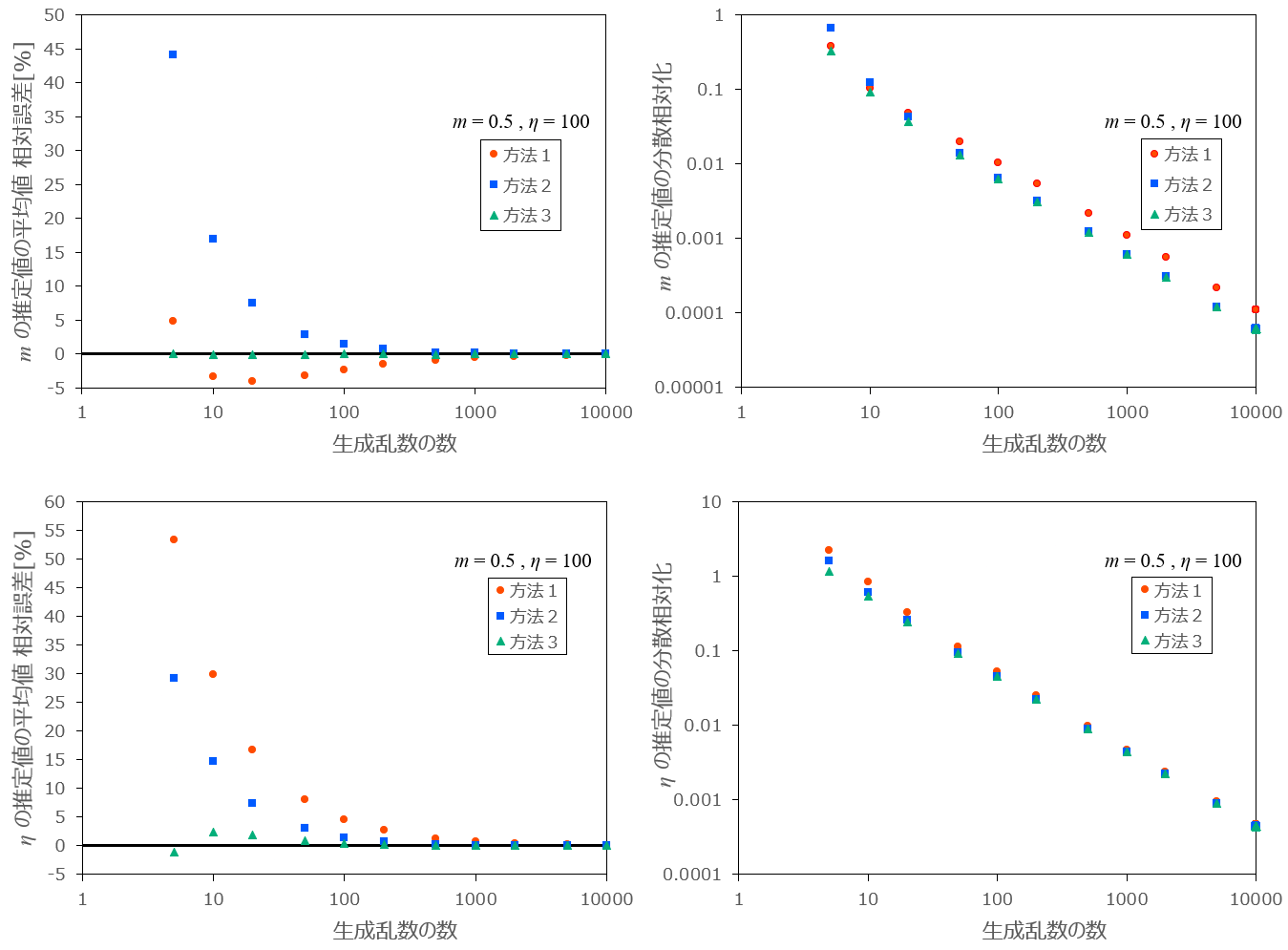
図12:生成乱数の数
まとめ
以上の結果から、
[4] Python ソースコード
以下、簡易シミュレーションで使用したPythonのソースコードです。
numpy,pandas は標準ライブラリにありませんので、インストールが必要になります。
バージョン情報
python : 3.12.0
numpy : 1.26.2
pandas : 2.1.3
import numpy as np
import math
import pandas as pd
import warnings
import os
# ηの推定量の補正係数の計算
def CALC_CETA(m,num):
c= 1.0
for k in range(1,num):
c *= k/(k + 1/m)
c *= m * (num ** (1/m)) / math.gamma(1/m)
#c = num ** (1/m) * math.gamma(num) / math.gamma(num+1/m)
return c
# num個の乱数によるパラメータの推定を num_of_times 回実施した計算結果を出力する
def CALC(m,eta,num,num_of_times):
# 計算結果の配列の定義
m_hat1_arr = np.empty(0) #確率紙による m
eta_hat1_arr= np.empty(0) #確率紙によるη
m_hat2_arr = np.empty(0) #最尤推定による m
eta_hat2_arr = np.empty(0) #最尤推定によるη
m_hat3_arr = np.empty(0) #最尤推定の改良版による m
eta_hat3_arr= np.empty(0) #最尤推定の改良版によるη
# mの最尤推定量補正用 a_m, b_m
a_m = 0.725703999
b_m = -1.361581962
# 累積分布関数F(x)の生成 #累積分布関数は乱数に依存しないため、ループの外で実施し、計算量を減らす
F = np.arange(1,num+1)
F= (F-0.3)/(num +0.4) #メジアンランク Benardの近似式
# y = ln {-ln(1-F(x)) } の計算
y=np.log(-np.log(1-F))
y_bar = np.average(y)
# num個の乱数によるパラメータの推定を num_of_times 回実施
for i in range(num_of_times):
# 最尤推定の m が発散 -> 乱数再生成のループ
while(1):
# Retryフラグ
retry_flag = 0
# 乱数生成用
rng = np.random.default_rng()
# U(0,1)の一様乱数を生成
u = rng.random(num)
# 昇順に並び替え
u = np.sort(u)
# 逆関数法によりワイブル分布に従う乱数の生成
x = eta * (-np.log(1-u)) **(1/m)
logx = np.log(x)
logx_bar = np.average(logx)
# y = a * logx + b と線形近似し、最小二乗法による傾きaと切片bを計算
a = (np.dot(logx-logx_bar,y-y_bar) / np.sum((logx-logx_bar) ** 2))
b = y_bar - logx_bar * a
# a,bからパラメータm,ηの推定 -> 確率紙による推定
m_hat1 = a
eta_hat1 = np.exp(-b/a)
# ニュートン法による最尤推定のmの算出 L(m,η)の m 微分が 許容値以下になるまで反復計算
error = 1 #L(m,η)の m 微分の値初期値
rep=0 #反復回数
error_limit = 1e-8 #許容値
m_hat = m_hat1 # m の初期値 m0 は 確率紙による推定を使用
while (abs(error) >= error_limit):
try:
xm = x ** m_hat
xmlogx_ov_xm = np.sum(np.dot(xm,logx)) / np.sum(xm)
# g(m), g'(m) の計算
g_m = 1/m_hat + logx_bar - xmlogx_ov_xm
g_m_diff = - m_hat ** (-2) - np.sum(np.dot(xm,logx ** 2))/np.sum(xm) + xmlogx_ov_xm ** 2
#対数尤度関数の m 微分 d/dm lnL(m,η) = num * g(m)の計算
error = num * g_m
# mの更新
m_hat = m_hat - g_m / g_m_diff
# m の発散を検知 -> retry フラグ =1
except Exception as e:
#print(e)
retry_flag = 1
break
# m の反復計算が100回を超える場合は計算方法を変更
if 100 < rep <=200 :
m_hat = 1/2 * (1/( xmlogx_ov_xm -logx_bar) + m_hat )
#print(f'{i}回目:反復回数{rep}、m^={m_hat}、g(m)={g_m}、g\'(m)={g_m_diff}')
# 200回超えても計算が収束しない場合は乱数の生成からやり直し
elif rep > 200:
print(f'mの最尤推定の計算が収束しません。乱数を再生成します。')
break
rep += 1
# m の発散を検知 -> retryフラグ =1 -> 乱数再生成
# m 収束 -> retryフラグ=0 -> 続行
if retry_flag == 1:
print(f'{i}番目の試行:mの値{m_hat}が発散しました。乱数を再生成します。')
continue
else:
break
m_hat2 = m_hat
# m の補正
m_hat3 = m_hat * (a_m* num + b_m)/ (a_m* num + b_m +1)
# ηの計算
eta_hat2 = np.average(x ** m_hat2) ** (1/m_hat2)
eta_hat3 = eta_hat2 * CALC_CETA(m_hat3,num)
# 各方式の推定の計算結果を配列に追加
m_hat1_arr = np.append(m_hat1_arr,m_hat1)
eta_hat1_arr = np.append(eta_hat1_arr,eta_hat1)
m_hat2_arr = np.append(m_hat2_arr,m_hat2)
eta_hat2_arr = np.append(eta_hat2_arr,eta_hat2)
m_hat3_arr = np.append(m_hat3_arr,m_hat3)
eta_hat3_arr = np.append(eta_hat3_arr,eta_hat3)
# 平均、不偏分散を計算
m_hat1_avg = np.average(m_hat1_arr)
m_hat1_var = np.var(m_hat1_arr,ddof=1)
eta_hat1_avg = np.average(eta_hat1_arr)
eta_hat1_var = np.var(eta_hat1_arr,ddof=1)
m_hat2_avg = np.average(m_hat2_arr)
m_hat2_var = np.var(m_hat2_arr,ddof=1)
eta_hat2_avg = np.average(eta_hat2_arr)
eta_hat2_var = np.var(eta_hat2_arr,ddof=1)
m_hat3_avg = np.average(m_hat3_arr)
m_hat3_var = np.var(m_hat3_arr,ddof=1)
eta_hat3_avg = np.average(eta_hat3_arr)
eta_hat3_var = np.var(eta_hat3_arr,ddof=1)
#結果出力用配列の作成
outdata = np.array([m, eta, num, num_of_times,
m_hat1_avg, m_hat1_var, eta_hat1_avg, eta_hat1_var,
m_hat2_avg, m_hat2_var, eta_hat2_avg, eta_hat2_var,
m_hat3_avg, m_hat3_var, eta_hat3_avg, eta_hat3_var
])
#結果の二次元配列化 (列を結合できるように)
outdata = outdata.reshape(len(outdata),1)
#結果表示
print(f'確率紙によるmの推定値平均、分散:{m_hat1_avg}、{m_hat1_var}')
print(f'確率紙によるηの推定値平均、分散:{eta_hat1_avg}、{eta_hat1_var}')
print(f'最尤推定によるmの推定値平均、分散:{m_hat2_avg}、{m_hat2_var}')
print(f'最尤推定によるηの推定値平均、分散:{eta_hat2_avg}、{eta_hat2_var}')
print(f'最尤推定の改良版によるmの推定値平均、分散:{m_hat3_avg}、{m_hat3_var}')
print(f'最尤推定の改良版によるηの推定値平均、分散:{eta_hat3_avg}、{eta_hat3_var}')
return outdata
def main():
## numpy の 計算オーバーフローのwarning を error としてtry except を作動させ、乱数の生成までやり直し
# m の発散が頻発する場合は条件を変更した方がよい。(mが大きい、nが小さいほど発散しやすい)
warnings.resetwarnings()
warnings.simplefilter('error')
#出力結果格納用配列
dataset = np.empty((16,0))
# パラメータの設定
m = 0.5 #形状パラメータ
eta = 100 #尺度パラメータ
num = 10 #生成乱数の個数
num_of_times = 100000 #試行回数
No = 1
m_start, m_stop, m_step = 0.1, 5.0, 0.1
num_start, num_stop,num_step = 4, 50, 1
#for m in np.arange(m_start,m_stop+m_step,m_step):
#for eta in np.array((1,2,5,10,20,50,100,200,500,1000,2000,5000,10000)):
for num in np.arange(num_start,num_stop+1,num_step):
#for num in np.array((5,10,20,50,100,200,500,1000,2000,5000,10000)):
#計算条件の表示
print(f'No.{No}: m={m}, η={eta}, 乱数の数={num}, 試行回数={num_of_times} の条件で計算中')
#各パラメータの計算結果の列を結合
dataset = np.append(dataset,CALC(m,eta,num,num_of_times),axis=1)
No +=1
# ファイル出力
## 表題作成
index1 = ['mの真値', 'ηの真値', '生成乱数の個数', '試行回数',
'確率紙:mの推定値の平均', '確率紙:mの推定値の分散', '確率紙:ηの推定値の平均','確率紙:ηの推定値の分散',
'最尤推定:mの推定値の平均', '最尤推定:mの推定値の分散', '最尤推定:ηの推定値の平均','最尤推定:ηの推定値の分散',
'最尤推定改良版:mの推定値の平均','最尤推定改良版:mの推定値の分散','最尤推定改良版:ηの推定値の平均','最尤推定改良版:ηの推定値の分散'
]
header1 = []
for i in range(dataset.shape[1]):
header1.append(f'No.{i+1}')
# データフレーム形式に変換
pd_out = pd.DataFrame(dataset,columns=header1, index=index1)
#ファイル名の設定
outname0 = f'm={m}_η={eta}_乱数の数={num}_試行回数={num_of_times}'
outname = outname0 + '.csv'
#ファイル名が重複する場合、ファイル名を自動変更
filenum = 1
while( os.path.exists(outname) ):
outname = outname0 + f'_{filenum}.csv'
filenum += 1
# csvデータ出力 #shift-jis でないとエクセルで文字化け
pd.DataFrame(pd_out).to_csv(outname, encoding='shift-jis')
input('計算が完了しました。ENTERで最初からやり直します。')
if __name__ == "__main__":
while(1):
main()
Discussion