説明可能なAI(Explainable AI:XAI)の各手法調査(2)
の続き。
各手法
この記事で紹介する各手法は以下のような時系列で発表されている。
時系列順に一つずつ、調べていったことのメモを書いていこうと思う。
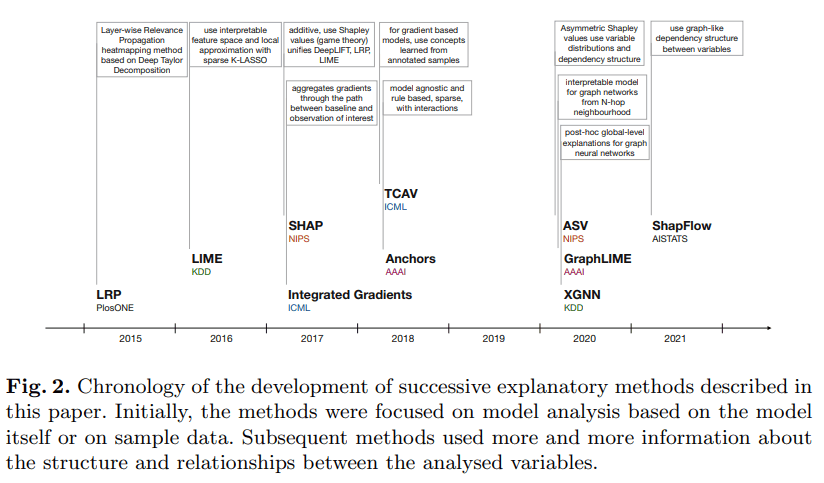
(https://link.springer.com/chapter/10.1007/978-3-031-04083-2_2 より引用)
今回はTCAV以降を調べていく。
TCAVs(Testing with Concept Activation Vectors)
論文
TCAVはCAVs(Concept Activation Vectors)というニューラルネットワークの内部状態を人間に解釈可能な空間に落とし込んだベクトルを用いて行うテスト手法のこと。
ニューラルネットワークの内部状態は基本的に人間が見ても理解できないようなものになっている。各セルごとに重みが存在しそれぞれが複雑に接続しあっているため、内部状態は行列やベクトルの単位で観測するしかない。しかしCAVでは、人間に理解可能な概念をモデル内部のベクトル空間に落とし込み、その概念(Concept)と目的とするものの方向微分(その概念が目的のものにどれほど影響しているか)を求めることで概念の貢献度を算出する。

(https://arxiv.org/abs/1711.11279 より引用)
図中の(a)は与える概念(縞模様)の正例と負例(ランダムサンプリング)を用意したものとなっている。その概念のデータから(c)の学習済みモデルを使ってCAV(概念のベクトル)を学習する。このベクトル
ちなみに方向微分の式は下のように表すことができるため、特定の層の重みベクトルの勾配とCAVの内積をとることで貢献度を算出できる。
(https://arxiv.org/abs/1711.11279 数式(1)を引用)
この手法の特徴としては、以下のようなものが挙げられる。
- 概念(Concept)を学習データとは別に定義できる
- 重要度の項目を人間がカスタマイズできる
- 基本的に画像データのみ対応(考え方自体は画像以外にも応用できるかも)
- 勾配を求める必要はあるが、推論を複数回しなくてよいので高速
上の方ではあまり触れていなかったが、概念(Concept)は学習データとは別に学習させてCAVを作り出すので、すでに学習済みのモデルでも新しい概念を導入して重要度を可視化することが出来る(カスタイマイズ性が非常に高い)。従来の手法は基本的にピクセル・スーパーピクセル単位でヒートマップを可視化するようなものが多かったが、この手法はそれより抽象的な「概念」を人が定義することが出来るため、より人間が理解しやすい可視化をすることが出来る。
実装はTensorFlowとpytorchの二つが見つかった。
Anchors
論文
Anchorsはモデルに依存しないXAI手法の一つで、”アンカー”という名の通り、特徴量(もしくは入力の一部分)を固定することによって、その他の部分を変化させて出力がどう動くかを確認し、固定すると出力があまり変化しなくなる特徴量を見つける。その特徴量は言い換えると、その出力に大きく寄与している特徴量であるため重要といえる。
論文中では自然言語の例が挙げられており、Anchorsでは”not good/bad”などの複数の単語でポジティブ/ネガティブを測ることが出来る。理由としては、Anchorsは特徴量を特定の値に固定して出力がどう変化するかを観測するので、"not"と"good"を固定してほかのサンプルを生成したときに多くがネガティブになると、"not good"の組み合わせがネガティブなのだと予測が出来るため。

Anchorsの特徴的な部分は、局所的な部分を忠実に再現するところで、論文中でもLIMEなどの既存の手法と比較して説明されている。下の図右側では、AnchorsとLIMEの機械学習モデルの近似方法の違いを可視化している。「+」「ー」が与えられたデータ(正例、負例)を表しており、LIMEはその周辺のサンプルから線形モデルで正例と負例を分ける境界線を学習する(図中の点線)。一方でAnchorsは与えられたデータと同じラベルの周辺のサンプルから「どれくらいの範囲がそのラベルのものか」を求める(図中の長方形)。
図中で説明していることとしては、LIMEなどの既存の手法では線形モデルで局所的なサンプルを使って近似をしまうため誤った説明をしてしまうことがあるが、Anchorsは特徴量を固定することで出力が変化しない範囲を探すような手法で、全体的な予測の説明は行わないため忠実な説明をしているということだ。(多分イメージとしては、LIMEは境界線を引いてしまうので「モデルはこういう風に特徴量を使っています!」と全体的な説明をして間違うことがあるが、Anchorsは「このデータの特徴量はこの値のときにこういう役割をします。」と正しく局所的な説明をしている、という感じだと思う)

Anchorsの実装はここにあった。
基本的にモデルに依存しないため、モデル自体のライブラリは特に制限されていなさそう。
ただ、モデルの入出力の形には依存するので注意が必要そうなのと、長い間更新されていないので動かない可能性もある。
ASVs(Asymmetric Shapley values)
論文 ※詳しい部分はあまり理解できていない...
ASVs(Asymmetric Shapley values)は、ゲーム理論に基づいた特徴量の重要度を評価する手法の一つで、モデルに依存しないXAI手法となっている。ゲーム理論の一部であるシャープレイ値(Shapley Value)の考え方を用いて特徴量の貢献度を計算するが、通常のシャープレイ値よりもより公平にそれぞれの特徴量の重要度を求めることが出来る。
シャープレイ値は特徴量が特定の出力にどれくらい影響を与えるか(つまり貢献度)を算出するが、通常はすべてのプレイヤー(機械学習モデルの場合は特徴量)を同じように扱っている。具体的には、特徴量を一つずつ外したり(平均で置き換える、など)することで”特徴量がその値のときに出力にどう影響を与えるか”を算出することが出来る。
しかし、この方法だと特徴量同士の相互作用や因果関係を考慮できないという欠点がある。例えば、特徴量A, Bが存在し、その二つの間に因果関係があったとする。その場合に通常のシャープレイ値であれば特徴量A, Bどちらも同じような重要度になる(因果関係があるため持っている情報は近しいため)が、本来は因果関係の依存されている方(独立変数というのか...?)が重要度が高くなっていて欲しい。
そこで、ASVsでは”特徴量同士の組み合わせ”も考慮することで、上のような「因果関係があって片方のみ重要としたい場合」なども正しく重要度を算出することが出来る(詳しい式は論文を参照)。論文中に挙げられている例として収入の国勢調査がある。通常のシャープレイ値では婚姻状況や職業など様々な要因が重要であるという結果が出ているが、ASVsではそもそもその背後にある性別の差が最も重要とされている(性別によって婚姻状況や職業などの重要な特徴量も左右されている)。

実装は存在するが、あまりメンテナンスされておらずスター数も少ない。
GraphLIME
論文
GraphLIMEはグラフ構造データの説明可能性を向上される手法で、主にグラフニューラルネットワークのモデルに使用する。(グラフニューラルネットワークをあんまり勉強したことがないからこの手法は理解するのきついかも...)
Graph structured data has wide applicability in various domains such as physics, chemistry, biology, computer vision, and social networks, to name a few. Recently, graph neural networks (GNN) were shown to be successful in effectively representing graph structured data because of their good performance and generalization ability. GNN is a deep learning based method that learns a node representation by combining specific nodes and the structural/topological information of a graph. However, like other deep models, explaining the effectiveness of GNN models is a challenging task because of the complex nonlinear transformations made over the iterations. In this paper, we propose GraphLIME, a local interpretable model explanation for graphs using the Hilbert-Schmidt Independence Criterion (HSIC) Lasso, which is a nonlinear feature selection method. GraphLIME is a generic GNN-model explanation framework that learns a nonlinear interpretable model locally in the subgraph of the node being explained. More specifically, to explain a node, we generate a nonlinear
interpretable model from its N-hop neighborhood and then compute the K most representative features as the explanations of its prediction using HSIC Lasso. Through experiments on two real-world datasets, the explanations of GraphLIME are
found to be of extraordinary degree and more descriptive in comparison to the existing explanation methods.
(https://arxiv.org/abs/2001.06216 より引用)
詳しい内容を理解するのが難しそうなので、ここではAbstractからなんとなく理解する。
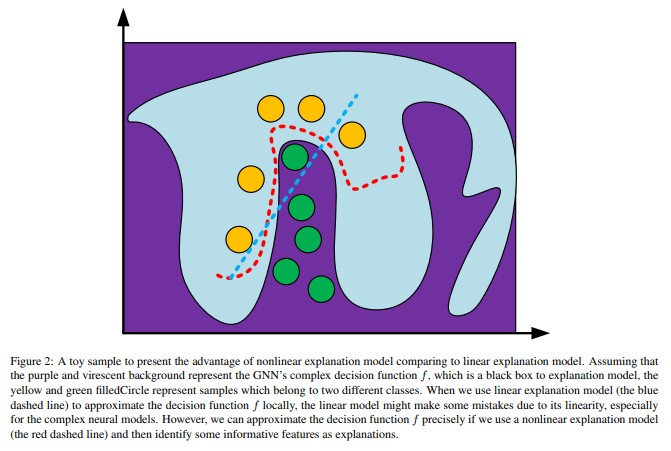
GNNはグラフ構造にはなっているものの、通常のNNと同様に内部構造を人間が理解することが非常に難しい。そのため、通常のLIMEのようにローカル解釈可能なモデルを使用して局所的なモデルの再現をするが、その際にヒルベルト・シュミット独立基準(Hilbert-Schmidt Independence Criterion, HSIC)Lassoのグラフを用いるそう(通常のLIMEは線形モデルで局所的なモデルの再現をする)。
通常のLIMEとは線形かどうかが大きく違うところなようで、下の図では通常のLIME(青の点線)とGraphLIME(赤の点線)で局所的により正確に近似できてるのは後者の方であることを説明している。図中の背景色は説明したい複雑なGNNの境界を表しており、その中にクラス別に色が決められているサンプルが存在している(このサンプルは説明したい入力の近傍のものを取ってきているよう)。
実装は以下に存在した。
XGNN
論文
XGNNはGraphLIMEと同様でGNNに適用するためのXAI手法となっている。GraphLIMEと違う点としては、単一の入力に対して説明をするのではなく、モデル全体の解釈をいくつかの入力グラフからひも解くというやり方を取っている所だと思う。
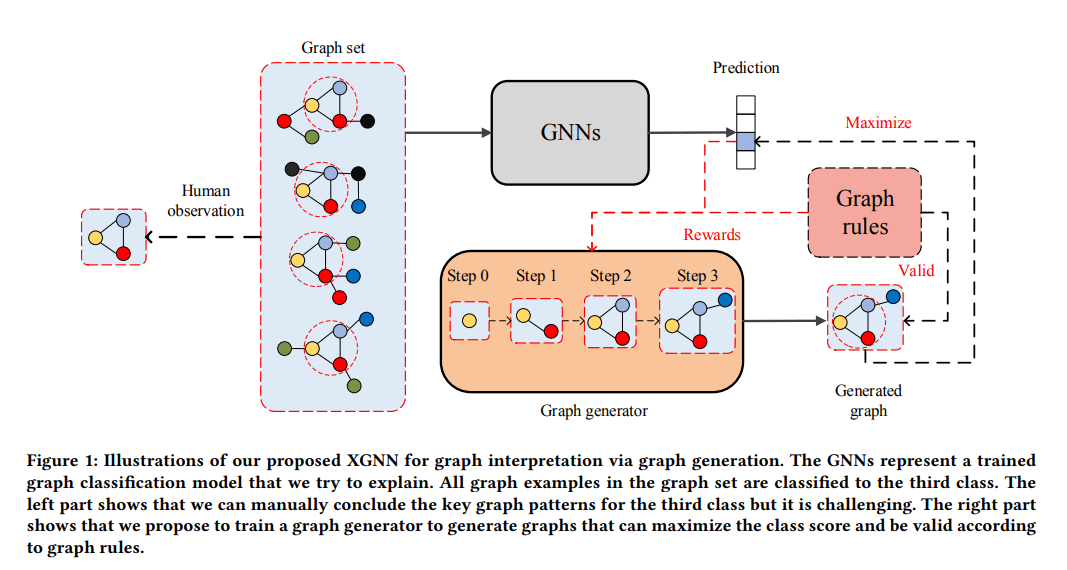
(https://arxiv.org/abs/2006.02587 より引用)
上記の図はXGNNの全体的なプロセスを説明している。まず、GNNsと書かれている説明したいグラフニューラルネットがいくつか存在する。図の左側では人間からみると特定のパターンのグラフが重要であることが分かるが、あくまでこの規模のグラフでしかそういったことは困難である。そこで、図右側で予測結果(報酬)が最大になるように新たにグラフを生成し、その過程で人間が見つけたような根本的な構造をみつける。それをそのモデルの解釈とする手法がXGNNとなっている。
(詳しい説明は論文を参照。あんまり理解できている気がしない...w)
実装は見つからなかった。
一応それっぽいのはあったが、ドキュメントが書いてないのであまり使えそうではない。
ShapFlow
論文
ShapFlow(Shapley Flow)はゲーム理論のシャープレイ値に基づいた手法であるSHAPなどが抱える、”特徴量間の相互作用・因果関係を考慮できない”という課題を解決する手法となっている。具体的には、従来の方法は特徴量間の因果関係のノードに重要度を割り当てるのに対し、ShapFlowではエッジ(つまり特徴量同士の関係)に重要度を割り当てることで上記の課題を解決している。
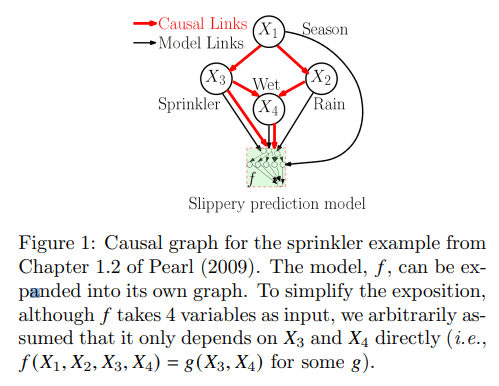
また、ASVsも特徴量同士の因果関係を考慮できる点では同じだが、因果関係のもととなる特徴量を必要以上に重視してしまうという欠点が存在する。下の図は論文中でASVsとShapFlowの比較に用いられているもので、ASVsでは特徴量
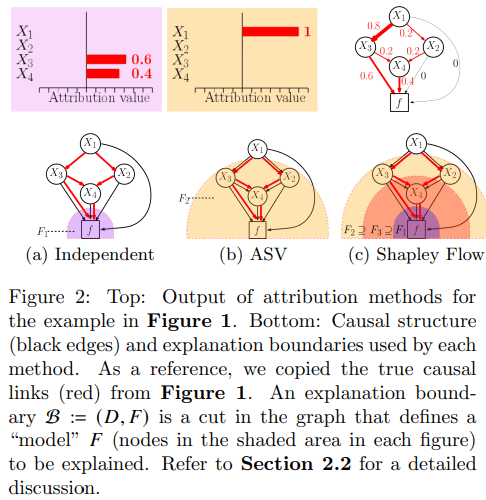
そのため、可視化をする際には単純に各特徴量に数値を割り当てるだけではなく、下のようにグラフを可視化することが出来る。
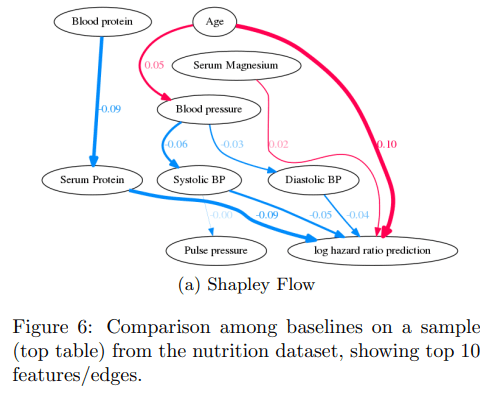
実装
Discussion