ベクトル解析 \subset 微分形式?
ベクトル解析とは、極めて雑に言えば、ベクトル微分演算子\nablaに関する技術です。ここに外積、内積、スカラー積、テンソル積などのベクトル演算を混ぜ込むことで、様々な物理量とその変化を捉えることができます。
一方の微分形式は、(数学的にはともかく)物理的には、低次元境界尽き部分多様体で積分されるような要素です。余接束の外積によってヤコビアン相当の共変性が成分にビルトインされているため、ある領域での積分を、単にその成分を重積分するだけで得ることができ、ストークス定理によって、近接作用論的な物理量の収支を表現するのに向いています。k次の微分形式はk次元の領域で積分されることが想定されています。
ところで、ベクトル解析で議論されている物理を微分形式で置き換えようという風潮 がずっとあります(要出典)が、その試みはいまいち皮相的に終わっているように思えます。(例えば、正規直交座標でのマクスウェル方程式を微分形式で書き直して、ポテンシャル関数に帰着させて満足するとか)
実のところベクトル解析の議論がすべて普通の微分形式でカバーできているのかというと、できていません。例として、マクスウェルの応力テンソルの発散を計算する議論を見てみましょう。
マクスウェルの応力テンソルとは、通常のベクトル解析では次です。
T = \mathbf{E}\mathbf{D} - \frac{1}{2}\mathbf{E}\cdot\mathbf{D}\mathbb{I} + \mathbf{H}\mathbf{B} - \frac{1}{2}\mathbf{H}\cdot\mathbf{B}\mathbb{I}
ここで、ボールド体でのベクトルが隣接しているところは、ダイアド積とよばれるもので、つまるところ単なるテンソル積\otimesです。この応力テンソルは応力の名の通り、面を通じて働く時間あたり運動量供給です。つまり、
F_A = \int_A T \cdot \mathbf{n}dS
と面要素の法線ベクトルとの内積を面積分すると、その面を通じて働く力=時間あたり運動量が得られるというものです。これの発散を計算してみましょう。
肝心なのは次の計算です。
\mathbf{X}(\nabla\cdot\mathbf{X})-\mathbf{X}\times(\nabla \times \mathbf{X}) = \nabla\cdot\left(\mathbf{X}\mathbf{X}-\frac{1}{2}\mathbf{X}\cdot\mathbf {X}\mathbb{I}\right)
ほんまか? \dagger物理学科の叡智\daggerたる公式
\epsilon_{ijk}\epsilon_{klm}=\delta_{il}\delta_{jm}-\delta_{im}\delta_{jl}
を脇に置いて計算してみましょう。
\begin{align*}
& \left(\mathbf{X}(\nabla\cdot\mathbf{X})-\mathbf{X}\times(\nabla \times \mathbf{X}) \right)_i\\
= & X_i(\partial_j X_j) - \epsilon_{ijk}\epsilon_{klm} X_j\partial_l X_m\\
= & X_i(\partial_j X_j) - (\delta_{il}\delta_{jm}-\delta_{im}\delta_{jl})X_j\partial_l X_m \\
= & X_i(\partial_j X_j) - X_j(\partial_i X_j) + X_j(\partial_j X_i)\\
= & X_i(\partial_j X_j) + X_j(\partial_j X_i) - X_j(\partial_i X_j)\\
= & (\nabla \cdot \mathbf{X}\mathbf{X})_i - \left(\nabla\cdot\frac{1}{2} (\mathbf{X}\cdot\mathbf{X})\mathbb{I}\right)_i
\end{align*}
確かに成り立っています。\epsilon_0\mathbf{E}=\mathbf{D},\mu_0\mathbf{H}=\mathbf{B}であることを考慮すると、
\begin{align*}
& \nabla\cdot T \\
= & \nabla\cdot \left(\epsilon_0\mathbf{E}\mathbf{E} - \frac{\epsilon_0}{2}\mathbf{E}\cdot\mathbf{E}\mathbb{I} + \frac{1}{\mu_0}\mathbf{B}\mathbf{B} - \frac{1}{2\mu_0}\mathbf{B}\cdot\mathbf{B}\mathbb{I}\right)\\
= & \epsilon_0(\mathbf{E}(\nabla\cdot\mathbf{E})-\mathbf{E}\times(\nabla \times \mathbf{E})) + \frac{1}{\mu_0} (\mathbf{B}(\nabla\cdot\mathbf{B})-\mathbf{B}\times(\nabla \times \mathbf{B}))\\
= & \mathbf{E}(\nabla\cdot\mathbf{D})-\mathbf{D}\times(\nabla \times \mathbf{E})+\mathbf{H}(\nabla\cdot\mathbf{B})-\mathbf{B}\times(\nabla \times \mathbf{H})
\end{align*}
マクスウェル方程式群
\begin{align*}
\nabla \cdot \mathbf{D} & = \rho\\
\nabla \times \mathbf{E} & = -\dot{\mathbf{B}}\\
\nabla \cdot \mathbf{B} & = 0\\
\nabla \times \mathbf{H} &= \mathbf{J} + \dot{\mathbf{D}}
\end{align*}
を代入すると
\begin{align*}
& \nabla\cdot T \\
= & \mathbf{E}\rho + \mathbf{D}\times \dot{\mathbf{B}} -\mathbf{B}\times(\mathbf{J} + \dot{\mathbf{D}}) \\
= & \mathbf{E}\rho + \mathbf{D}\times \dot{\mathbf{B}} + \mathbf{J}\times \mathbf{B} + \dot{\mathbf{D}} \times \mathbf{B} \\
= & \mathbf{E}\rho + \mathbf{J}\times \mathbf{B} + \frac{\partial}{\partial t}(\mathbf{D}\times \mathbf{B})
\end{align*}
これと"ガウス発散定理"(?)から
\begin{align*}
\int_{\partial N} T \cdot\mathbf{n} dS = \int_{N} (\mathbf{E}\rho + \mathbf{J}\times \mathbf{B})dV + \frac{d}{dt}\int_N (\mathbf{D}\times \mathbf{B})dV
\end{align*}
となり、領域Nでの運動量収支である「境界面からの運動量の出入り」=「領域内ローレンツ力による電荷への運動量」+ 「領域内電磁場の運動量の変化」が成り立ちます。
さて、この計算は微分形式ではカバーできていません。理由としては
- 応力テンソルは面積分でベクトルが得られるが、普通の微分形式はスカラーしか得られない。
- 応力テンソルは面積分するのに、法線ベクトル内積で積分する想定で次数が(1+1)になっている。
あたりです。面積分されるのなら、順当に行けば2形式であるべきです。しかしTは積分の結果ベクトルが得られるようにするために次数の1つはベクトルに費やされていて、残りの1次で2形式を代替しています。つまり、Tは一見\Gamma(TM\otimes TM)のような姿をしていますが、本当は\Gamma(TM \otimes \wedge^2 TM^*)ではないか?ということです。
共変外微分
こうした物をカバーできるようにするには、ベクトル値の微分形式を扱う必要があります。その場合外微分もそのままではだめで、共変外微分にする必要があります。とはいえ、完全に一般的なものを導入する意味はありません。だいたいそんなことをしたら簡便さが失われてしまい、何のために導入したんだということになります。一般相対論を組み合わせるのでもない限り、普通時空は平坦で曲率はゼロです。ホロノミーもありません。したがって、平行移動は経路によりません。接続も、その平坦な座標に沿った平行移動で定めます。要するに、計算に使う座標系だけ自由に取れるようにしたいわけです。
共変外微分の前に、共変微分を導入しましょう。平坦な空間でも共変微分を考慮する意味はあります。任意の座標系で正しい微分を計算できます。接空間・余接空間にLevi-Civita接続を入れます。これによる共変微分は、接ベクトル場X \in \Gamma(TM)なら
\nabla X = \nabla (X^i\partial_i) = \partial_i \otimes (dX^i + \omega^i_j X^j)
余接ベクトル場Z \in \Gamma(TM^*)なら
\nabla Z = \nabla (Z_i dx^i) = dx^i \otimes (dZ_i - \omega^j_i Z_j)
となる。接続形式\omega^i_jが接/余接で逆なのはもちろんこれらの内部積の微分がライプニッツを満たすようにするためです。\omega^i_jはクリストッフェル記号で
\omega^i_j = \Gamma^i_{jk} dx^k
と表現でき、捩率ゼロなので\Gamma^i_{jk} = \Gamma^i_{kj}です。この接続を用いて、共変外微分は、E\otimes \eta \in \Gamma(TM\otimes \wedge^k TM^*)に対して
D(E\otimes \eta) = \nabla E \wedge \eta +E \otimes d\eta
と定義できます。ちなみに、ファイバーの構造が自明なら、共変外微分は外微分に帰着します。最初の\nabla E \wedge \etaの外積は、\nabla Eによって発生した共変足と\etaを外積するということです。一般の接続ではD^2に曲率形式が現れますが、今平坦な空間しか考えないとしたので、D^2=0です。
Levi-Civita接続のもとでは、共変外微分は、共変微分で増えた反対称足を反対称化したものとみなせます。例えば、E\otimes f dx^{i_1}\wedge \dots dx^{i_k} \in \Gamma(TM\otimes \wedge^k TM^*)にたいして、そのまま共変微分すれば、微分形式の部分\wedge^k TM^*にも接続が現れます。
\begin{align*}
& \nabla E\otimes f dx^{i_1}\wedge \dots dx^{i_k}\\
= & (\nabla E) \otimes f dx^{i_1}\wedge \dots dx^{i_k}\\
+ & E \otimes \left(df\otimes dx^{i_1}\wedge \dots dx^{i_k} - f\left( \sum_p \Gamma^{i_p}_{jk}dx^k\otimes dx^{i_1}\wedge \dots dx^{i_{p-1}}\wedge dx^{j}\wedge dx^{i_{p+1}}\dots dx^{i_k} \right)\right)
\end{align*}
しかしk+1共変足を反対称化して規格化すると、dx^k \wedge dx^jが登場するため、\Gamma^i_{jk}=\Gamma^i_{kj}によって微分形式の接続項は消えます。
\begin{align*}
& \frac{(k+1)!}{k!}(\nabla E\otimes f dx^{i_1}\wedge \dots dx^{i_k}) (\mathbb{I}\otimes \mathfrak{A}_{k+1})\\
= & (\nabla E) \wedge f dx^{i_1}\wedge \dots dx^{i_k} + E \otimes \left(df\wedge dx^{i_1}\wedge \dots dx^{i_k}\right) \\
= & D( E\otimes f dx^{i_1}\wedge \dots dx^{i_k})
\end{align*}
したがって、捩率ゼロ条件のもとで、接/余接ベクトル値微分形式の共変外微分は
D(-) = (k+1)\nabla(-)\circ (\mathbb{I}\otimes \mathfrak{A}_{k+1})
で代用できます。ただし、\mathfrak{A}_kは、反対称化
\mathfrak{A}_k : dx^{i_1}\otimes \dots dx^{i_k} \mapsto \frac{1}{k!}\sum_{\sigma \in \mathfrak{S}_k} \mathrm{sgn}(\sigma)dx^{i_\sigma(1)}\otimes \dots dx^{i_\sigma(k)} = \frac{1}{k!}dx^{i_1}\wedge \dots dx^{i_k}
です。
道具をこのように用意して結局どうするのかというと、基本的には、外微分を共変外微分Dに置き換えるだけです。平坦なのでD^2=0は通常の微分形式と同じです。共変・反変が合わない場合は、Hodgeオペレータと計量を利用して添字を変えます。計量とHodgeはともに計量だけから得られる量で、かつ今微分をすべて共変微分で実施するのだから、Hodgeと計量は微分作用素からは定数のように処理することができます。これが共変微分を考える最大のご利益です。
ストークスの定理は、接/余接ベクトル値を潰すことで対処します。例えば、ある接ベクトル値k微分形式\etaを考えます。「平行な=共変微分がゼロな」余接ベクトル場Aを持ってきて内部積をとり、\langle A, \eta\rangleとすればこれはただのk形式です。
\begin{align*}
&\int_{\partial N} \langle A, \eta\rangle \\
= & \int_{N} d\langle A, \eta\rangle \\
= & \int_{N} \langle DA, \eta\rangle + \langle A, D\eta\rangle\\
= & \int_{N} \langle A, D\eta\rangle
\end{align*}
とすれば、これは\etaのA方向成分に関するストークスの定理とみなせます。これを線形独立なすべての平行なAについてまとめたものを
\int_{\partial N} \eta = \int_{N} D\eta
と標語的に記しているのだとすれば、通常のストークスのdをDに置き換えたものが成り立っているといえます。
道具は出揃いました。しかし、個々の計算規則は大したことなくても、テンソルの足や縮約がたくさん生えてきてかえって混乱してしまいます。ここまでのセットアップで、応力テンソルの発散を(接ベクトル値)微分形式として計算し直したいですが、結局計算が見づらく視認性が悪いのなら、何のために微分形式(ry
というわけで、やはりString Diagramをつかって計算を図示します。
図的に計算する
応力テンソルの発散を、String Diagramを使ってベクトル値微分形式の共変外微分として計算しましょう。ここでやることは次です。マクスウェル応力テンソルTを\Gamma(TM\otimes \wedge^2TM^*)の要素だとして定義し、その発散を取ります。そのときちゃんと共変外微分をつかって計算し、結果が\Gamma(TM\otimes \wedge^3 TM^*)になるようにするのです。そのうえで通常のベクトル解析のときと整合的な結果になれば良しとしましょう。
まず、利用可能な計算規則を列挙しましょう。なお、Hodgeオペレータと、varHodgeについては、前の記事を参照してください。
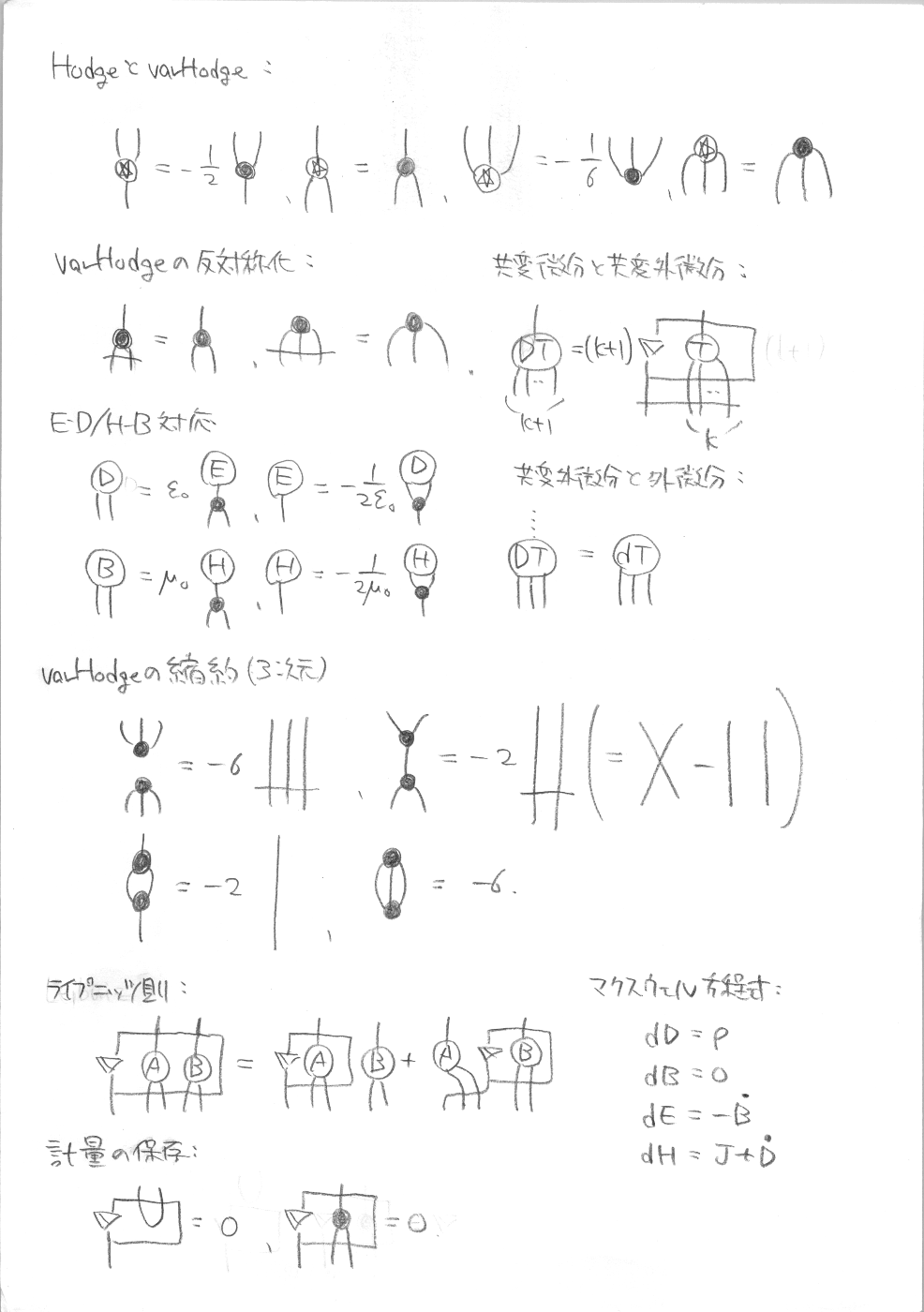
まず、先のベクトル解析のときの公式
\mathbf{X}(\nabla\cdot\mathbf{X})-\mathbf{X}\times(\nabla \times \mathbf{X}) = \nabla\cdot\left(\mathbf{X}\mathbf{X}-\frac{1}{2}\mathbf{X}\cdot\mathbf {X}\mathbb{I}\right)
に相当する式を示します。
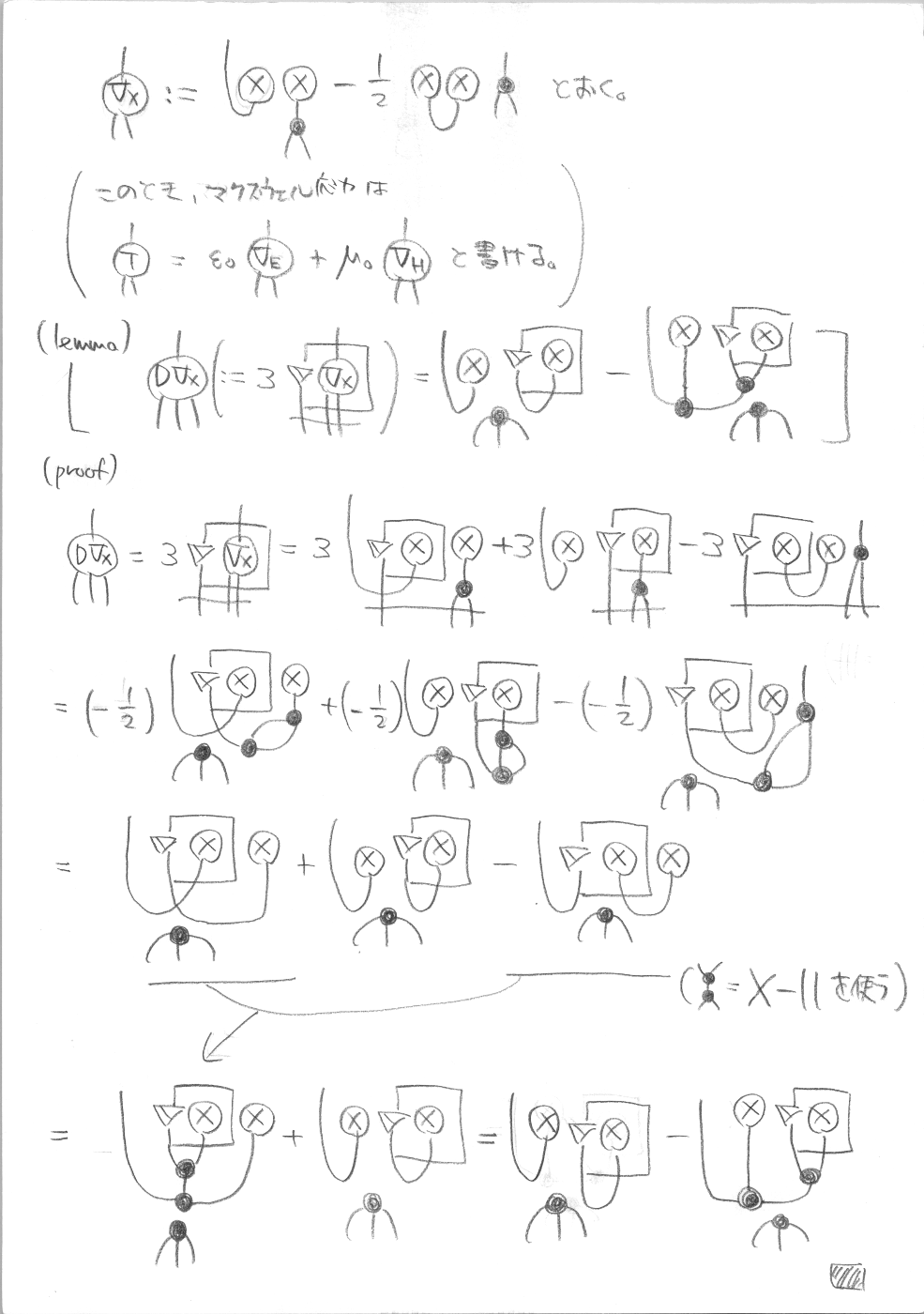
これを用いると
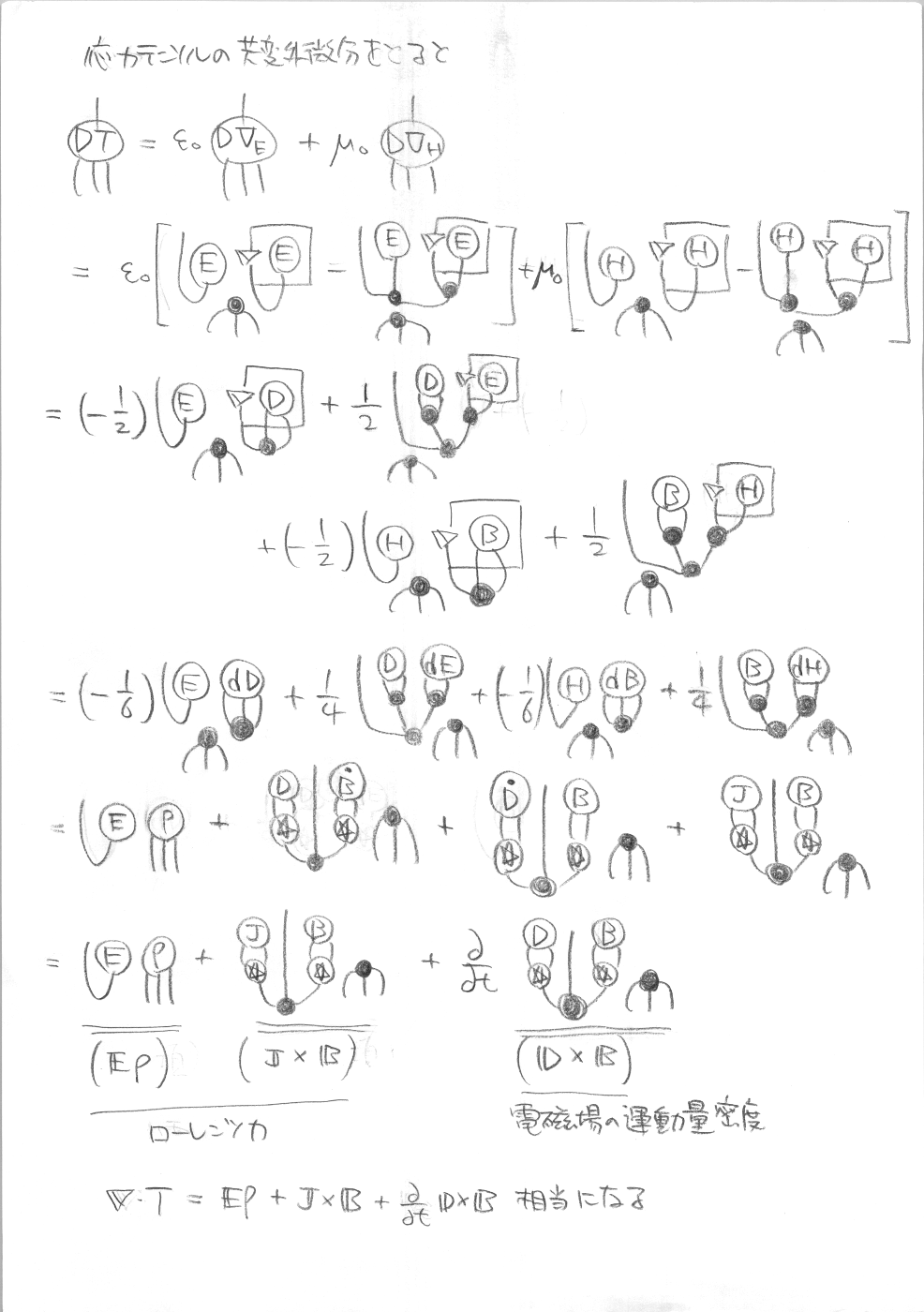
ということで、ちゃんとマクスウェル応力を接ベクトル値2形式として取り扱えてそうです。
めでたしめでたし...
って、怠すぎ〜〜〜〜〜〜〜〜〜〜〜〜!!!!!!!!!
かなり怠いので、よっっっっぽど共変性がほしくなる状況を除き、ベクトル解析が微分形式に置き換えられることは無いでしょう。多分。

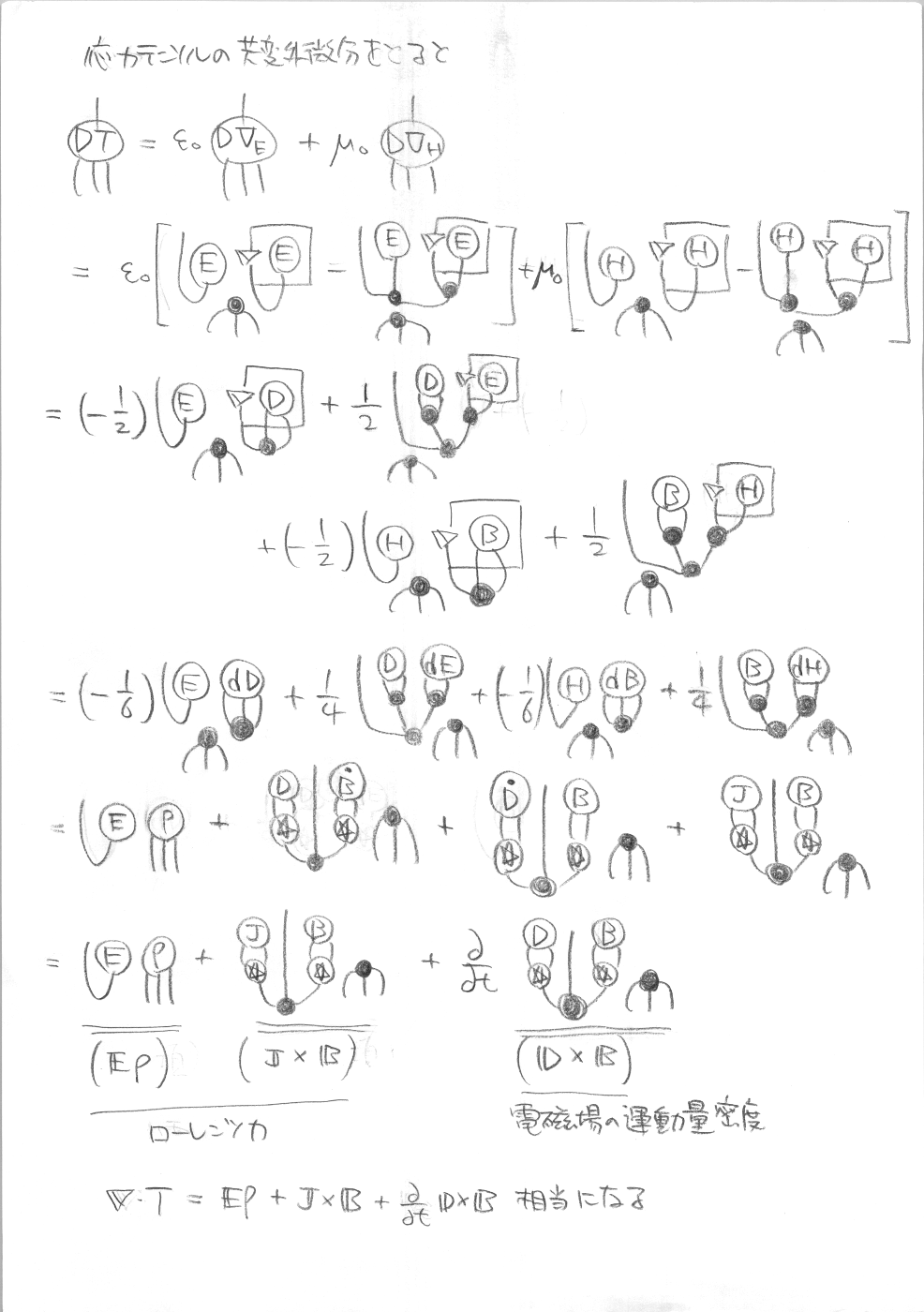
Discussion