Hodgeオペレータ
Hodgeオペレータというのがあります。微分幾何の教科書をみると出てくる定義は、
\alpha \wedge \star \beta = \langle \alpha,\beta \rangle_{\wedge^k} \mathrm{vol}
というものです。ここで注意として、外積は規格化調整なしの流儀を採用し、
dx^{i_1} \wedge dx^{i_2} \dots dx^{i_k} = \sum_{\sigma \in \mathfrak{S}_k} \mathrm{sgn}(\sigma) dx^{i_{\sigma(1)}} \otimes dx^{i_{\sigma(2)}} \dots dx^{i_{\sigma(k)}}
微分形式の内積は規格化調整を行うとします。
\langle \alpha,\beta \rangle_{\wedge^k} = \frac{1}{k!}\langle \alpha,\beta \rangle_{TM^{*\otimes k}}
ここで\langle -,- \rangle_{TM^{*\otimes k}}とは、計量gの逆行列h=g^{-1}を用いて、
\langle dx^i,dx^j \rangle_{TM^*} = h^{ij}
としたもののテンソル積です。もちろん\mathrm{vol}は体積形式
\mathrm{vol} = \sqrt{\mathrm{det}g}dx^{1} \wedge dx^{2} \dots dx^{n}
です。物理学におけるベクトル解析を微分形式で表現しようという風潮は前からずっとあり(要出典)そこではこのHodgeオペレータが非常に重要です。
明示的にする
このHodgeの定義は幾何学的ですが、陰的で扱いにくいです。とはいえ、これを計算するためにあまりに座標系にあまりにつよい制限を課したら、固有の性質が見えなくなります。このHodgeの定義をもう少し簡単にします。
まず、Hodgeは局所的に定義されており線形なので、dx^{i_1} \wedge dx^{i_2} \dots dx^{i_k}のような要素に対する作用を考えればその性質は尽きます。そこでこのHodgeを成分展開します。
\begin{align*}
&\star(dx^{i_1} \wedge dx^{i_2} \dots dx^{i_k}) \\
= & \sum_{l_{k+1} < l_{k+2} \dots l_{n}}A_{l_{k+1}l_{k+2} \dots l_{n}}(dx^{l_{k+1}} \wedge dx^{l_{k+2}} \dots dx^{l_{n}})
\end{align*}
ナンバリングされた添字をまとめてその添字の大文字で代表することにします。このL=\{l_{k+1},\dots l_{n}\}は、現時点では潜在的には1\dots nの部分集合をすべて走る可能性があります。Hodgeの定義に代入すると
\begin{align*}
&(dx^{j_1}\wedge dx^{j_2} \dots dx^{j_k}) \wedge \star(dx^{i_1} \wedge dx^{i_2} \dots dx^{i_k}) \\
=& \sum_{l_1 < l_2 \dots l_{n-k}}A_{l_{k+1}l_{k+2} \dots l_{n}}(dx^{j_1} \wedge\dots dx^{j_k}\wedge dx^{l_{k+1}}\wedge dx^{l_n}) \\
= & \langle dx^{j_1}\wedge dx^{j_2}\dots dx^{j_k},dx^{i_1}\wedge dx^{i_2}\dots dx^{i_k} \rangle_{\wedge^k}\mathrm{vol}\\
= & \frac{1}{k!}\langle dx^{j_1}\wedge dx^{j_2}\dots dx^{j_k},dx^{i_1}\wedge dx^{i_2}\dots dx^{i_k} \rangle_{TM^{*\otimes k}}\mathrm{vol}\\
= & \mathrm{det}h^{J|I} \mathrm{vol}
\end{align*}
となります。ここで\mathrm{det}h^{J|I}は、J添字行、I添字列だけを抽出したhの部分行列式です。同じ基底添字が発生すると外積はゼロになるので、J\cup L = \{1\dots n\}のときだけA_Lが残り、この式はL=\overline{J}(添字補集合)であるときのA_Lの値を決定します。つまり、
A_L = \mathrm{sgn}(\overline{L}L)\mathrm{det}h^{\overline{L}|I}\sqrt{\mathrm{det}g}
ということであり、
\begin{align*}
&\star(dx^{i_1} \wedge dx^{i_2} \dots dx^{i_k}) \\
= & \sum_{L=\{l_{k+1}\dots l_n\} \subset \{1\dots n\}}\mathrm{sgn}(\overline{L}L)\mathrm{det}h^{\overline{L}|I}\sqrt{\mathrm{det}g}(dx^{l_{k+1}} \wedge dx^{l_{k+2}} \dots dx^{l_{n}})
\end{align*}
と成分展開が得られます。ただし、\mathrm{sgn}(\overline{L}L)とは、\{1\dots n\}を\overline{L}Lに並び替えるときの符号とします。
まだ複雑です。ここまでは、成分展開するときの基底の選び方について何も制限していませんでした。単純化のために次の仮定をしてみます。:「dx^{i_1},\dots dx^{i_k}と、それ以外の基底ベクトルは直交している」
そうすると、計量と逆計量は、ともにI=\{i_1\dots i_k\},\overline{I}=\{i_{k+1}\dots i_n\}の間でブロック対角化されます。
g = \begin{bmatrix}
g^I & 0 \\
0 & g^{\overline{I}} \\
\end{bmatrix},
h = \begin{bmatrix}
h^{I} & 0 \\
0 & h^{\overline{I}} \\
\end{bmatrix}
すると\mathrm{det}h^{\overline{L}|I}は、L=\overline{I}のとき以外は、空の行、空の列が交じることになり、ゼロとなります。したがって、次が成り立ちます。
\star (dx^{i_1}\wedge dx^{i_2}\dots dx^{i_k}) = \mathrm{sgn}(i_1\dots i_n)\mathrm{det}h^{I}\sqrt{\mathrm{det}g}dx^{i_{k+1}}\wedge dx^{i_{k+1}}\dots dx^{i_n}
ブロック対角化された行列の行列式は各ブロックの行列式の積なので、これを整理すると、I=\{i_1\dots i_k\},\overline{I}=\{ i_{k+1}\dots i_n \}の添字における基底が直交している時、
\star (\sqrt{\mathrm{det}g^{I}}dx^{i_1}\wedge dx^{i_2}\dots dx^{i_k}) = \mathrm{sgn}(I\overline{I})\sqrt{\mathrm{det}g^{\overline{I}}}dx^{i_{k+1}}\wedge dx^{i_{k+2}}\dots dx^{i_n}
となります。したがって、Hodgeオペレータとは、部分空間の体積要素を直交補空間の体積要素に置き換える演算子 であるという解釈ができます。
再度幾何化する
このHodgeの解釈を利用して、もう一段簡略化します。逆計量h=g^{-1}はTM \otimes TM \simeq (TM^* \rightarrow TM)のテンソル場だと思えます。また、体積形式はそれ自体n形式なので、TM^{\otimes n}の双対でもあります。これを利用して、k形式\betaに対して次の内部積を考えます。
\frac{1}{k!}\mathrm{vol}(h^{\otimes k}\circ \beta,-)
実はこれはHodgeオペレータに一致します。このことを示すために、やはり最も簡単なdx^{i_1} \wedge dx^{i_2} \dots dx^{i_k}に対する像を考えます。同様に、dx^{i_1},\dots dx^{i_k}以降の基底ベクトルはこれに直交するように選択されているとします。
\begin{align*}
& h^{\otimes k}\circ dx^{i_1} \wedge dx^{i_2} \dots dx^{i_k} \\
= & \sum_{J,\sigma \in \mathfrak{S}_k}\mathrm{sgn}(\sigma)h^{i_{\sigma(1)}j_1}\dots h^{i_{\sigma(k)}j_k}\partial_{j_1}\otimes \dots \partial_{j_k}
\end{align*}
を代入すると
\begin{align*}
& \frac{1}{k!}\mathrm{vol}(h^{\otimes k}\circ dx^{i_1} \wedge dx^{i_2} \dots dx^{i_k},-) \\
= & \frac{1}{k!}\sum_{J,\sigma^\prime \in \mathfrak{S}_n,\sigma \in \mathfrak{S}_k}\mathrm{sgn}(\sigma^\prime)\mathrm{sgn}(\sigma)h^{i_{\sigma(1)}j_1}\dots h^{i_{\sigma(k)}j_k}\delta^{\sigma^\prime(1)}_{j_1}\otimes \dots \delta^{\sigma^\prime(k)}_{j_k}dx^{\sigma^\prime(k+1)}\otimes \dots dx^{\sigma^\prime(n)} \sqrt{\mathrm{det}g}
\end{align*}
直交性を仮定したことで、J=\{j_1\dots j_k\}は\sigma^\prime(1)\dots \sigma^\prime(k)の範囲を重複なく動いたときだけ値をとることになり、\sigma^\primeに関する和は、その残りの\sigma^\prime(k+1)\dots \sigma^\prime(n)を反対称化します。\mathfrak{S}_k,Jが、1\dots kの順列並び替えをあわせて2回行うため、hの部分行列式はk!重複して出現し、係数と相殺します。
\begin{align*}
= & \mathrm{sgn}(I\overline{I})\mathrm{det}h^{I}\sqrt{\mathrm{det}g} dx^{i_{k+1}}\wedge \dots dx^{i_n}\\
= & \star (dx^{i_1},\dots dx^{i_k})
\end{align*}
これによって、Hodgeオペレータの幾何学的かつ陽的な公式が得られました。
\star \beta = \frac{1}{k!} \mathrm{vol}(h^{\otimes k}\circ \beta,-)
つまり Hodgeオペレータとは、体積形式との内(部)積を規格化したもの というわけです。
図的直感を持ち込む
つまるところ、Hodgeオペレータとは、(逆)計量と体積形式をいい感じに合成したものに過ぎないとわかりました。ただし、それは高階のテンソルの内部積を伴うので、1行数式では直感が働きません。高階テンソルの合成演算を直感的に描くには、やはりString Diagramでしょう。任意階テンソルのなす対称モノイダル圏のString Diagramを考えます。反変ベクトル脚は上へ、共変ベクトル脚は下にワイヤを伸ばすと向きの約束をします。
ここで特殊記法として、計量と逆軽量を

とターンワイヤを使って表現します。また、反対称化
\mathfrak{A}_k : dx^{i_1}\otimes \dots dx^{i_k} \mapsto \frac{1}{k!}\sum_{\sigma \in \mathfrak{S}_k} \mathrm{sgn}(\sigma)dx^{i_\sigma(1)}\otimes \dots dx^{i_\sigma(k)} = \frac{1}{k!}dx^{i_1}\wedge \dots dx^{i_k}
を、横断する線
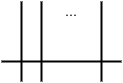
で表現します。さて、前節までの計算によればHodgeオペレータとは計量と体積形式と内部積で書けるのだから、それ自体テンソルであって
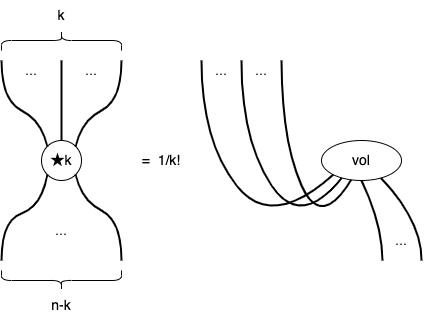
ということになります。Hodgeはそれ自体、符号を除けば逆演算 \star \circ \star = (-1)^{k(n-k)}であったことを思い出すと、この逆演算\star^{-1}は
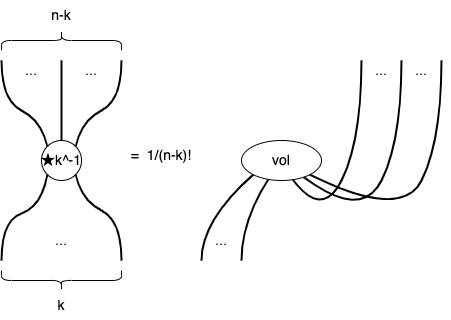
です。しかし、線がクロスしている箇所があって不格好ですね? また、k!,(n-k)!などの係数が登場したりkに依存するのも面倒です。そこで、Hodgeの変種、varHodgeを次のように定義してしまいましょう。
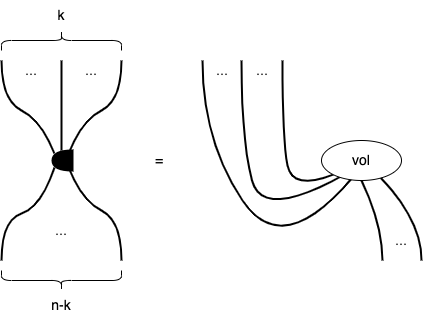
こうすると、例えば、varHodgeの最左添字の上下を計量で実施しても、係数を再調整する必要がなくなります。
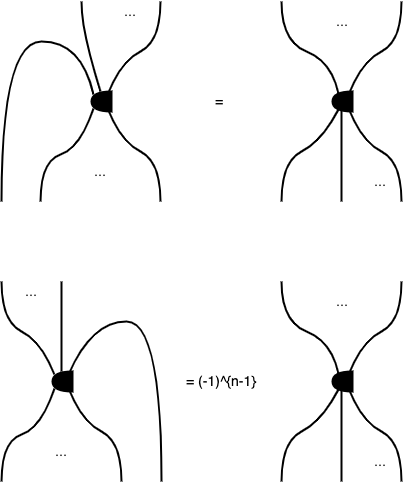
ただし、varHodgeの右側添字を上げ下げする場合は、体積形式の足を入れ替えることになるので、(-1)^{n-1}の修正が必要です。そのことを表すために、varHodgeのシンボルは、右側だけ切り欠いておきます。なお、これは奇数次元で考えているときには不要になるので、例えば3次元のときは完全に回転対称なシンボルで計算しても曖昧さがありません。
Hodgeが微分形式の間の写像であり、常に反対称化がかかることと、それ自体が逆写像に比例することから、次の 演算規則 が得られます。
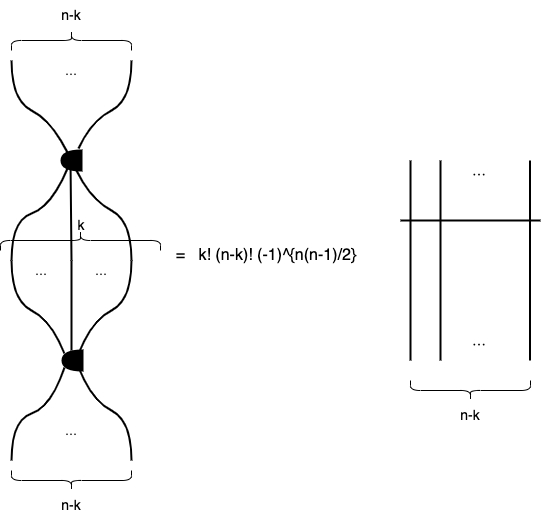
-1の冪が複雑ですが、これは次元nで決まるので、それほど苦ではないと思います。
例として3次元の場合を見てみましょう。
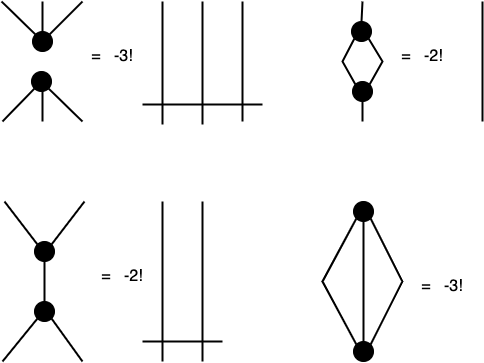
左下の式は物理学科の叡智(?)たる公式
\epsilon_{ijk}\epsilon_{klm} = \delta_{il} \delta_{jm} -\delta_{im} \delta_{jl}
そのものですね(足の添字の入れ替えに注意)
このように書き(描き)下すと、Hodgeオペレータもそんな凶悪な存在ではないように見えます。実際この演算規則は、完全反対称テンソルの計算規則そのものです。しかし、一般の計量つき多様体の任意の座標系でこれができるというのがポイントです。完全反対称テンソルの計算は、実は直交座標でなかったとしても成り立つということです。また、ここで導入した体積形式と、計量による添字の上げ下げは、すべて計量テンソルだけから作られています。ということは、計量を保つ共変(外)微分(Levi-Civita接続とかの)にたいして不変であり、Hodge,varHodge,ターンワイヤー、体積形式はすべて共変(外)微分を貫通することになります。









Discussion