プログラミングにおける周期的境界条件
はじめに
プログラミングにおける周期的境界条件は少し厄介なので備忘録もかねてまとめた。
使用言語はJuliaだが、ChatGPTでも使って好きな言語に書き換えて欲しい。
序章
周期的境界条件
よく物理のテキストでみる周期的境界条件は次の形である:
ここで、
物理的には、
シミュレーションでの例
これを、1次元のシュミレーションで考えてみよう。
システムを
- 注意
正確にはx=0 x=a x \in [0,a) x\in(0,a]
具体例
具体的な数値で考えてみよう。上の設定で、
(これはかつてのRPGでずっと右に行き続けると、左から出てくることと同じである。)
実際に、シミュレーションをしてみよう。今回は
using Plots
anim =@animate for t in -1.0:0.1:2.0
scatter([t], [0], label = "t = $t", ylims = (-1, 1), xlims = (-2, 2))
end
gif(anim, "anim.gif", fps = 10)
function periodic_boundary_conditions(x, L) # x: 位置, L: 系の長さ
if x > L
x -= L # x = x - L と同じ
elseif x < 0
x += L # x = x + L と同じ
end
return x
end
anim =@animate for t in -1.0:0.1:2.0
scatter([periodic_boundary_conditions(t, 1)], [0], label = "t = $t", ylims = (-1, 1), xlims = (-2, 3))
end
gif(anim, "anim_periodic_boundary_conditions.gif", fps = 10)
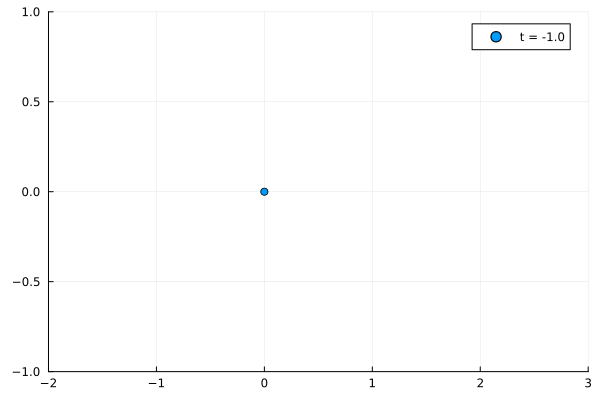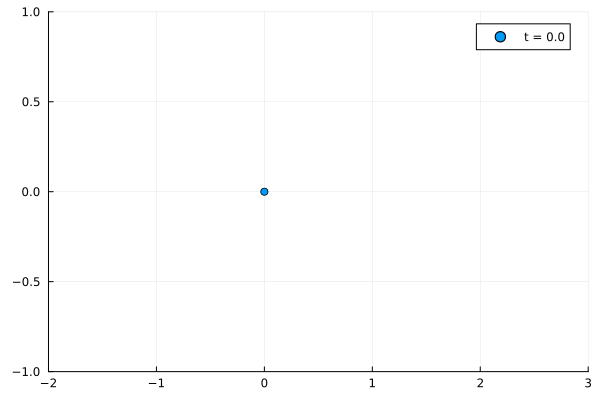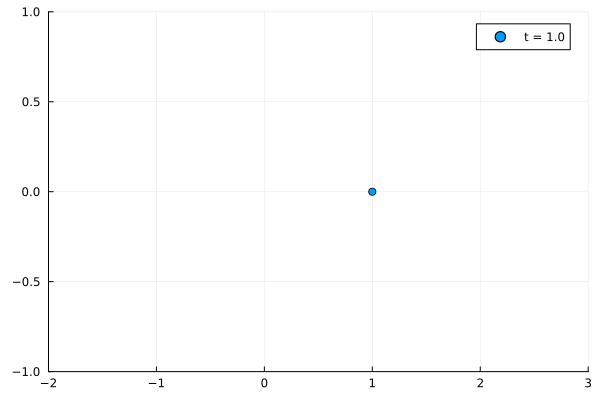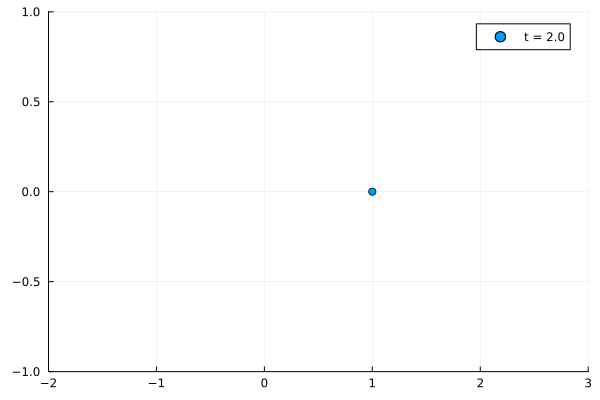
期待していた tの範囲は同じにしてある。インチキをしているわけではない!!。念の為。)
2次元の場合
それぞれの軸で1次元でやったものを行えば良い。すなわち、
function 2D_PBCs(x,y,Lx,Ly) #x,y:粒子のx,y座標. Lx, Ly:x,yそれぞれの系の長さ
if x > L
x -= Lx # x = x - L と同じ
elseif x < 0
x += Lx # x = x + L と同じ
end
if y > Ly
y -= Ly
elseif y < 0
y += Ly
return x,y
end
任意のシステムサイズの場合
英語版の周期的境界条件のwiki https://en.wikipedia.org/wiki/Periodic_boundary_conditions に書いてある。 "Practical implementation: continuity and the minimum image convention" という節を参照すること。
(英語読めないよって人は google 翻訳とか DeepL とか AI を使えばよい。)
多粒子の場合
粒子が
本章
序章では、粒子の位置をシステムの中に引き戻す方法を述べた。上の操作だけでよいのだろうか?
実は、例えば、粒子間距離に依存する力が働くときは上の状況だけでは上手くいかない。
相互作用があるときの周期的境界条件
簡単のため、2粒子系を考え、システムを
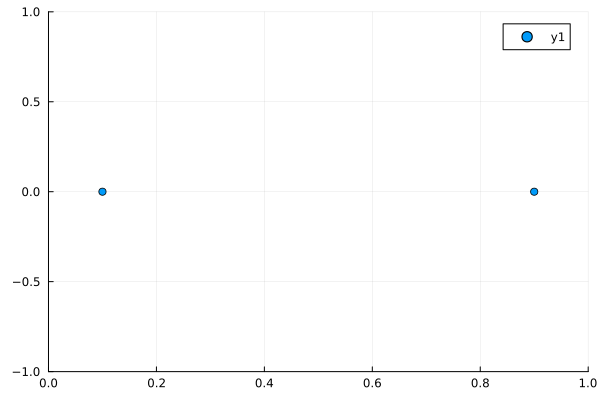
この場合は、2粒子間の距離

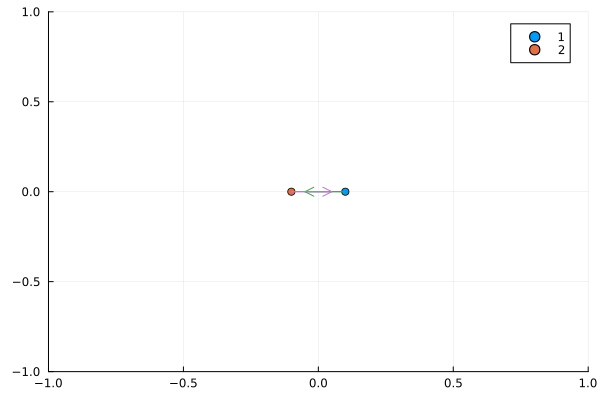
私達はどちらを採用すべきなのだろうか?
何度も繰り返すが、周期的境界条件というのは平行移動したところも同じとみなせるものであった。これは、同じ系を(1次元の場合は)右と左に張り合わせたものである
次に、力の向きについて考えよう。周期的境界条件を考えないときは粒子1に働く力は
まとめると今回の場合は次のようになる。
-
r > 0.5 r r-1 -
r < -0.5 r r+1 - それ以外は何もしない。
プログラミングのコードで書けば、
r = x1 - x2 # x1, x2 はそれぞれの粒子の位置
if r > 0.5 # 系のサイズを1とした。
r -= 1. # 1. は 1.0 の省略記法
elseif r < -0.5
r += 1.
end
これを一般化すれば、周期的境界条件の英語版 wiki(上記リンク)にあった(B)が得られる。
多次元の場合
例えば、2次元であれば
結論
シミュレーションにおける周期的境界条件で大事なことは次の2つになる。
- 粒子の位置に適用すること。
- 粒子間距離に適用すること。
実装するためのコードは次のようになる。(英語版 wiki のコードを Julia で書き換えただけ。)
if x < -L / 2 # L:システムサイズ, x: 粒子の位置
x -= L
elseif x > L / 2
x += L
end
r = x1 - x2 # x1, x2: 粒子 1, 2 の位置
if r > L / 2
r -= L
elseif r < - L / 2
r += L
end
今後の予定
周期的境界条件の具体例は書いていないので、2次元で相互作用を重力ポテンシャルにしたときの多体運動のコードを書く予定(予定は未定)。
2024年6月21日追記
補足
*1
張り合わせたものというのは、

一方、境界条件を適用し
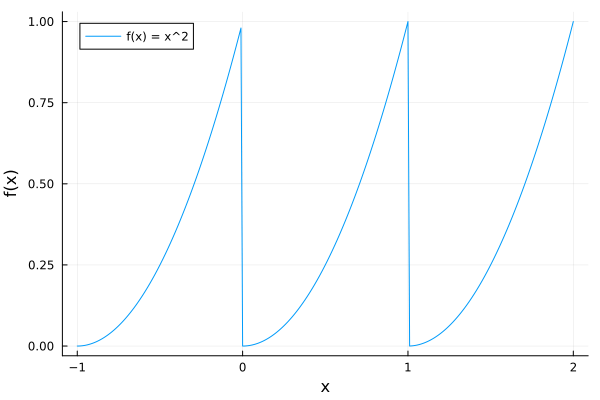
P.S.
インチキではないことの証明として上の画像のソースコードをおいておく。
f(x) = x^2
plot(f, -1, 2, label = "f(x) = x^2", xlabel = "x", ylabel = "f(x)")
f(x) = x^2
x = [i for i in -1:0.01:2]
x_PBCs = [PBCs(i, 1) for i in x] # PBCsは一番最初にかいた自作関数と同じ
y = f.(x_PBCs)
plot(x, y, label = "f(x) = x^2", xlabel = "x", ylabel = "f(x)")
Discussion