周期的境界条件で4体問題のシミュレーション
はじめに
先日、周期的境界条件について説明した。
今回はそれを使って、粒子間に重力が働く場合のシミュレーションのコードを書いた。
注意
計算が Runge-Kutta の 4 次なので、アニメーションはほとんど参考にならない。特に、粒子が非常に近い部分にいるときの動きは適当である。正確な多体問題の計算を行いたいのであれば、他の人が書いたものを参考にしてほしい。ここでは、周期的境界条件の具体的な使い方を記述するためのものである。
シミュレーションのコード
2次元の4粒子系でシミュレーションを行った。以下、Julia のコード
N_x = 14 # x方向の粒子数
N_y = 16 # y方向の粒子数
L = 1.0 # 箱の大きさ
N = 4 # 全粒子数
Position = zeros(N, 2)
Velocity = zeros(N, 2)
Force = zeros(N, 2)
Position_pre = zeros(N, 2)
Velocity_pre = zeros(N, 2)
Force_pre = zeros(N, 2)
dt = 0.0001 # 時間刻み幅
t_max = 0.50 # 時間の最大値
U = 1e6 # 相互作用の大きさ(ポテンシャルの強さ)
d0 = 1.0 / N_x # 相互作用の距離
dx = 1.0 / 14.0 # x方向の粒子間の距離
dy = 1.0 / 16.0 # y方向の粒子間の距離
# 初期配置の設定
function Initial_position()
Position[1, :] .= [0.5, 0.5]
Position[2, :] .= [0.3, 0.2]
Position[3, :] .= [0.4, 0.4]
Position[4, :] .= [0.6, 0.6]
end
# 初期速度の設定
function Initial_velocity()
Velocity[1, :] .= [1.0, 0.0]
Velocity[2, :] .= [2.0, 2.0]
Velocity[3, :] .= [1.0, 2.0]
Velocity[4, :] .= [2.0, 2.0]
end
# 力の計算
function calc_force()
for i in 1:N
Force[i, :] .= 0.0
end
for i in 1:N
for j in 1:N
if i != j
dist_x = -Position[i, 1] + Position[j, 1]
dist_y = -Position[i, 2] + Position[j, 2]
# 周期的境界条件
if dist_x > L / 2.0
dist_x -= L
elseif dist_x < -L / 2.0
dist_x += L
end
if dist_y > L / 2.0
dist_y -= L
elseif dist_y < -L / 2.0
dist_y += L
end
r_ij = sqrt(dist_x^2 + dist_y^2)
Force[i, 1] += dist_x / r_ij^3 # 重力の場合
Force[i, 2] += dist_y / r_ij^3
end
end
end
end
# Runge-Kutta 法の実装
function Runge_Kutta()
k1 = zeros(N, 2)
k2 = zeros(N, 2)
k3 = zeros(N, 2)
k4 = zeros(N, 2)
l1 = zeros(N, 2)
l2 = zeros(N, 2)
l3 = zeros(N, 2)
l4 = zeros(N, 2)
# Save initial positions and velocities
copyto!(Position_pre, Position)
copyto!(Velocity_pre, Velocity)
# k1, l1
# 周期的境界条件は適用してもよいがRunge-Kuttaの最後で適用しているので無駄。
# 力は計算する必要がある(はず)
calc_force()
for i in 1:N
k1[i, 1] = dt * Velocity[i, 1]
k1[i, 2] = dt * Velocity[i, 2]
l1[i, 1] = dt * Force[i, 1]
l1[i, 2] = dt * Force[i, 2]
end
# k2, l2
for i in 1:N
Position[i, 1] = Position_pre[i, 1] + k1[i, 1] / 2.0
Position[i, 2] = Position_pre[i, 2] + k1[i, 2] / 2.0
Velocity[i, 1] = Velocity_pre[i, 1] + l1[i, 1] / 2.0
Velocity[i, 2] = Velocity_pre[i, 2] + l1[i, 2] / 2.0
# 周期的境界条件
if Position[i, 1] >= L
Position[i, 1] -= L
end
if Position[i, 1] < 0
Position[i, 1] += L
end
if Position[i, 2] >= L
Position[i, 2] -= L
end
if Position[i, 2] < 0
Position[i, 2] += L
end
end
# 粒子の位置を更新したので、力も計算し直し
calc_force()
for i in 1:N
k2[i, 1] = dt * Velocity[i, 1]
k2[i, 2] = dt * Velocity[i, 2]
l2[i, 1] = dt * Force[i, 1]
l2[i, 2] = dt * Force[i, 2]
end
# k3, l3
for i in 1:N
Position[i, 1] = Position_pre[i, 1] + k2[i, 1] / 2.0
Position[i, 2] = Position_pre[i, 2] + k2[i, 2] / 2.0
Velocity[i, 1] = Velocity_pre[i, 1] + l2[i, 1] / 2.0
Velocity[i, 2] = Velocity_pre[i, 2] + l2[i, 2] / 2.0
if Position[i, 1] >= L
Position[i, 1] -= L
end
if Position[i, 1] < 0
Position[i, 1] += L
end
if Position[i, 2] >= L
Position[i, 2] -= L
end
if Position[i, 2] < 0
Position[i, 2] += L
end
end
calc_force()
for i in 1:N
k3[i, 1] = dt * Velocity[i, 1]
k3[i, 2] = dt * Velocity[i, 2]
l3[i, 1] = dt * Force[i, 1]
l3[i, 2] = dt * Force[i, 2]
end
# k4, l4
for i in 1:N
Position[i, 1] = Position_pre[i, 1] + k3[i, 1]
Position[i, 2] = Position_pre[i, 2] + k3[i, 2]
Velocity[i, 1] = Velocity_pre[i, 1] + l3[i, 1]
Velocity[i, 2] = Velocity_pre[i, 2] + l3[i, 2]
if Position[i, 1] >= L
Position[i, 1] -= L
end
if Position[i, 1] < 0
Position[i, 1] += L
end
if Position[i, 2] >= L
Position[i, 2] -= L
end
if Position[i, 2] < 0
Position[i, 2] += L
end
end
calc_force()
for i in 1:N
k4[i, 1] = dt * Velocity[i, 1]
k4[i, 2] = dt * Velocity[i, 2]
l4[i, 1] = dt * Force[i, 1]
l4[i, 2] = dt * Force[i, 2]
end
# Update positions and velocities
for i in 1:N
Position[i, 1] = Position_pre[i, 1] + (k1[i, 1] + 2.0 * k2[i, 1] + 2.0 * k3[i, 1] + k4[i, 1]) / 6.0
Position[i, 2] = Position_pre[i, 2] + (k1[i, 2] + 2.0 * k2[i, 2] + 2.0 * k3[i, 2] + k4[i, 2]) / 6.0
Velocity[i, 1] = Velocity_pre[i, 1] + (l1[i, 1] + 2.0 * l2[i, 1] + 2.0 * l3[i, 1] + l4[i, 1]) / 6.0
Velocity[i, 2] = Velocity_pre[i, 2] + (l1[i, 2] + 2.0 * l2[i, 2] + 2.0 * l3[i, 2] + l4[i, 2]) / 6.0
if Position[i, 1] >= L
Position[i, 1] -= L
end
if Position[i, 1] < 0
Position[i, 1] += L
end
if Position[i, 2] >= L
Position[i, 2] -= L
end
if Position[i, 2] < 0
Position[i, 2] += L
end
end
end
Position_plot = zeros(N, 2, Int(t_max / dt)) # gifをつくるために、粒子の位置を各tで保存
Initial_position()
Initial_velocity()
calc_force()
N_t = Int(t_max / dt)
for t in 1:N_t
Position_plot[:, :, t] .= Position
Runge_Kutta()
end
anim = @animate for i in 1:10:N_t
scatter(Position_plot[:, 1, i], Position_plot[:, 2, i], xlim=(0, 1), ylim=(0, 1), legend=false)
end
gif(anim, "output.gif", fps = 30)
解説
注意点は2つある。
1つ目は、粒子間に働く力(重力)を計算するときに粒子間距離を使うため、前回記事の周期的境界条件を適用する必要があること。
2つ目は、Runge-Kutta の関数中で時間を少し進めるので、その分だけ粒子の位置が変わることである。これは同時に、重力も変わるということである。そのため、システムサイズから出ていないことをきちんと確認することと、力を計算し直す事が必要である。よって、k,lについて計算するときに周期的境界条件を適用する。
この2つさえわかってしまえば、周期的境界条件を適用することは簡単である。
gif
上のコードを実行すると次の gif が得られる。これだと周期的境界条件のありがたみがわからないと思うので、初期位置と初期速度を極端な場合にしてみよう。
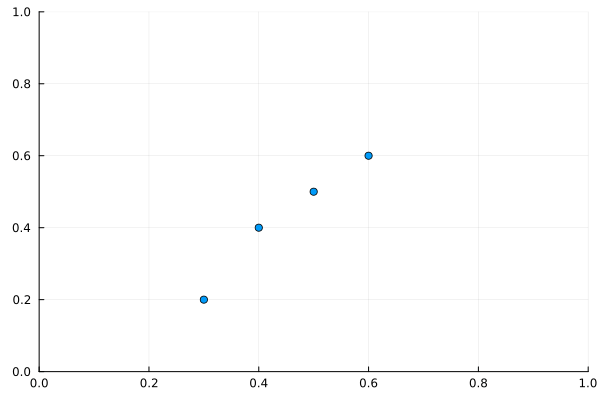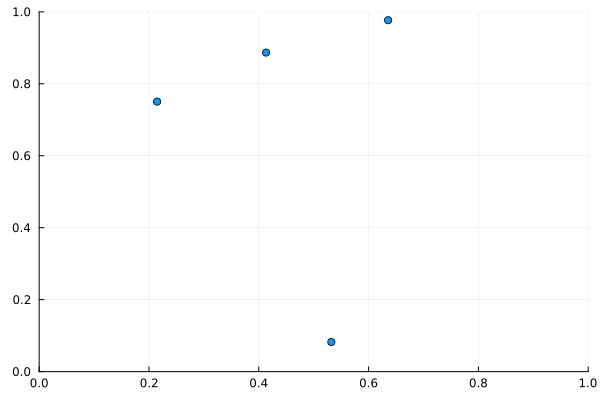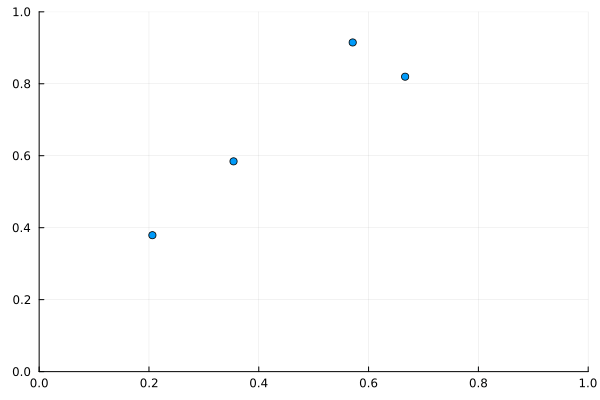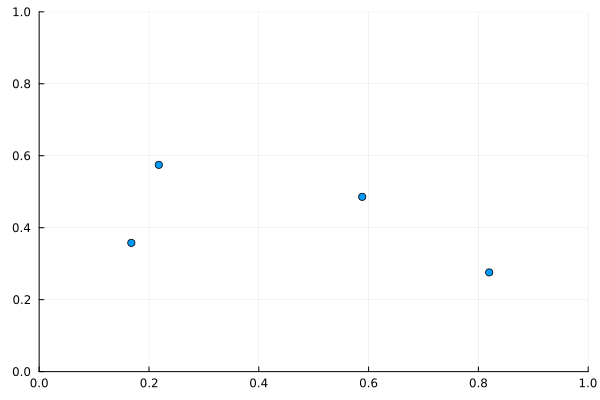
次の gif は初期配置を
function Initial_position()
Position[1, :] .= [0.0, 0.]
Position[2, :] .= [0.1, 0.1]
Position[3, :] .= [0.1, 0.0]
Position[4, :] .= [0.9, 0.9]
end
function Initial_velocity()
Velocity[1, :] .= [0.0, 0.0]
Velocity[2, :] .= [0.0, 0.0]
Velocity[3, :] .= [0.0, 0.0]
Velocity[4, :] .= [0.0, 0.0]
end
に変更したものである。
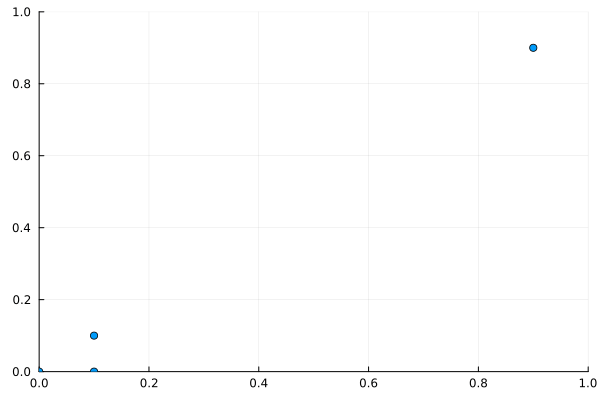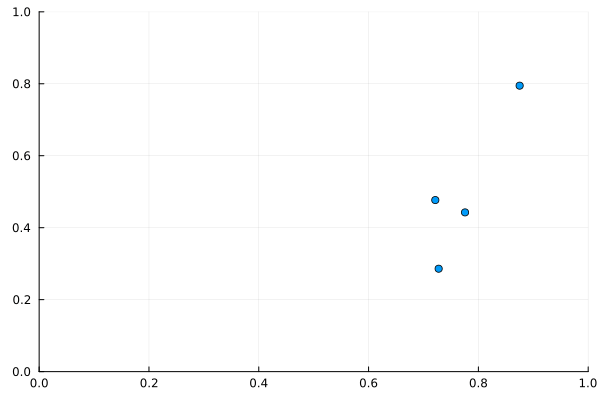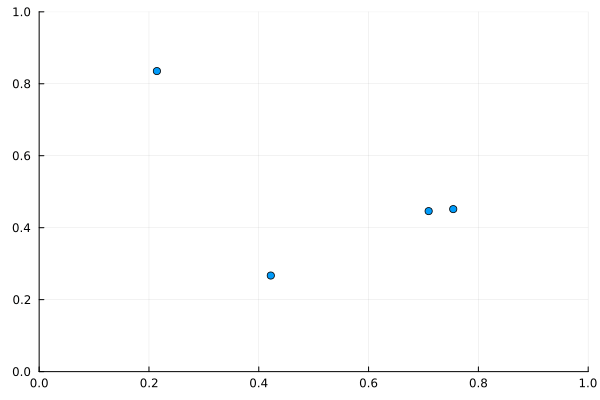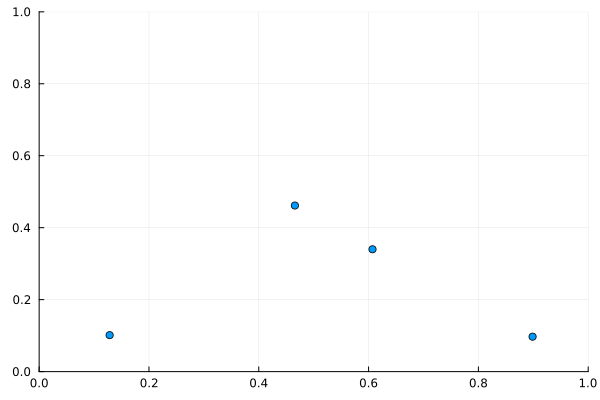
これを見ると、粒子間距離について周期的境界条件が適用されていることがわかるだろう。すなわち、右上の粒子が左下の粒子たちに引っ張られて、左下から出てくることである。
粒子間距離について周期的境界条件を適用しなければ、右上の粒子は当然距離が遠すぎるためほとんど動かないはずである。動いたとしても、右上から左下に進んでいくはずだ。
Discussion