🚗

さださんの楽曲でしりとりをする

2022/12/04に公開

数理最適化

tech

この記事は数理最適化アドベントカレンダー2022三日目の記事です。

一年というものは短いものですね。ついこないだ2022年を迎えたかと思いきや、もうすぐ2023年のお正月です。さて、年の初めはさだまさし♪年の終わりもさだまさし♪ということで、さださんの楽曲名でしりとりをしたいと思います。

ご存知の通り、さださんはこれまでに非常に多くの曲を発表されていて、その数は優に500曲を超えています。しりとりをするにはちょうど良い曲数でしょう。しりとりをしながらさださんの曲を聴いて、元旦の今夜も生でさだまさしにそなえましょう。

急ぐ人はこちらの結果をご利用ください。

最長しりとり問題と巡回セールスマン問題

今回は数理最適化のアドベントカレンダーですから、数理最適化を使ってしりとりに取り組みます。より正確には、「与えられた単語辞書（今回はさださんの楽曲タイトル）を使って、最も長いしりとり」を求めます。これは最長しりとり問題とも呼ばれています。

では、どのようにすると最長しりとり問題を解けるでしょうか？ぼくは、曲タイトルを順々に巡っていくという意味で、巡回セールスマン問題に近そうだなぁと思いました。そこで、巡回セールスマン問題に対する解法を修正すれば良いだろうと考えました^[1]。

tsp like
都市の代わりに曲タイトルを巡っていると考えられる

巡回セールスマン問題との違いは以下の3点です。定式化する際にこの辺りに注意しながら修正していけば良さそうです。

巡回路にはなっていない
- 巡回セールマン問題では、全ての都市を巡って帰ってくる必要がある。しりとりにはその概念はない
最小化ではなく最大化
- 巡回セールスマン問題では、距離やコストを最小化するが、ここでは巡るタイトル数の最大化が目的となる
全てのタイトルを巡る必要はない
- 巡回セールスマン問題では、全ての都市を巡ることが前提となっているが、しりとりでは必ずしも全てのタイトルを巡ることができるとは限らない
しりとりになっていなければいけない

データ準備

データ準備は、以下の流れで行いました。結果、全部で573曲のデータセットが出来上がりました。

楽曲のリストを入手
- さださんの楽曲がまとまっているサイトから抽出しました
- 抽出した楽曲は Google Spreadsheet にまとめました
タイトル名をひらがなに機械的に変換
- こういったサービスを利用して機械的にひらがなに変換
独自に定めたルールに則って、人手で修正
- 長音で終わるものは母音を採用することとしました
- 数字やアルファベットで開始・終了するものもひらがなに変換しました
- サブタイトルの処理は悩みましたが、今回は全て含めることとしました
接頭・接尾を抽出
- 単純にひらがなに変換したものの一文字目と最終文字を利用することとしました

作業中の Google Spreadsheet

巡回セールスマン問題（ポテンシャル定式化）

データが準備できたので、具体的な定式化に取り組みます。まず、ベースとなる巡回セールスマン問題についてみていきましょう。巡回セールスマン問題の定式化については、いろいろなサイトで紹介されているので、そちらを参考にすると良さそうです。巡回セールスマン問題については知っているよ！という方はポテンシャル定式化にお進みください

定数

まず、訪問先となる都市のインデックスを $i,j$ で表し、問題の入力データに相当する値（求めたい値ではなく、与えられる値。問題ごとに定数となります）を以下のように書くこととします。

$N\in \mathbb{N}$ : 都市数
$C_{ij}\in \mathbb{N}$ : 都市 $i$ から都市 $j$ に直接移動する時にかかるコストもしくは移動距離

決定変数

次に、決定変数（数理最適化で最適な値を決めたい変数）を以下のように定義します。

$x_{ij} \in \{0, 1\}$ : 都市 $i$ から都市 $j$ に直接移動する時は $1$ 、移動しない場合は $0$ となる変数
$z_{i} \in \{0,\dots,N\}$ ^[2]: 都市 $i$ の訪問順

$x_{ij}$ と $z_{i}$ 、どちらか一つが決まればもう片方も決まるので、一見どちらか一つで良さそうにみえますが、定式化の都合上それぞれを別々な変数として扱います。

目的関数

では、定数と決定変数を使って、目的関数（最大化・最小化したい値）を書きくだします。巡回セールスマン問題では、コストまたは移動距離を最小化したいので、以下のように書けます。

\min \sum_{ij}{C_{ij}x_{ij}}

制約条件

目的関数に含まれる $x_{ij}$ は自由に選べるわけではありません。まず、全ての都市 $i$ を一度だけ訪れなければいけません。また、訪れた都市からどこか別の都市に移動しなければいけません。

$\sum_{j} x_{ji} = 1 \quad \mathrm{for}\ \forall i$
- 全ての都市を一度だけ訪問する
$\sum_{j}x_{ij} = 1 \quad \mathrm{for}\ \forall i$
- 都市 $i$ を一度だけ出発する

これらに加え、部分巡回路を除去する必要があります。部分巡回路とは、以下の図のように全ての都市を回っていない巡回路のことです。部分巡回路の除去には色々な方法がありますが、わかりやすいのは、各都市に訪問順を振ってあげることです。

$x_{ij} = 1$ の時、 $z_{i} + 1 \leq z_{j} \quad \mathrm{for}\ j \neq 0,\ \forall i$

全ての都市を巡って、最後に戻ってくるときだけ順序が $0$ に戻るので、 $\mathrm{for}\ j \neq 0$ という条件をいれています。この条件は以下のように書き直せます（手を動かして確認してみてください)

$z_{i} + 1 - N(1 - x_{ij}) \leq z_{j} \quad \mathrm{for}\ j \neq 0,\ \forall i$

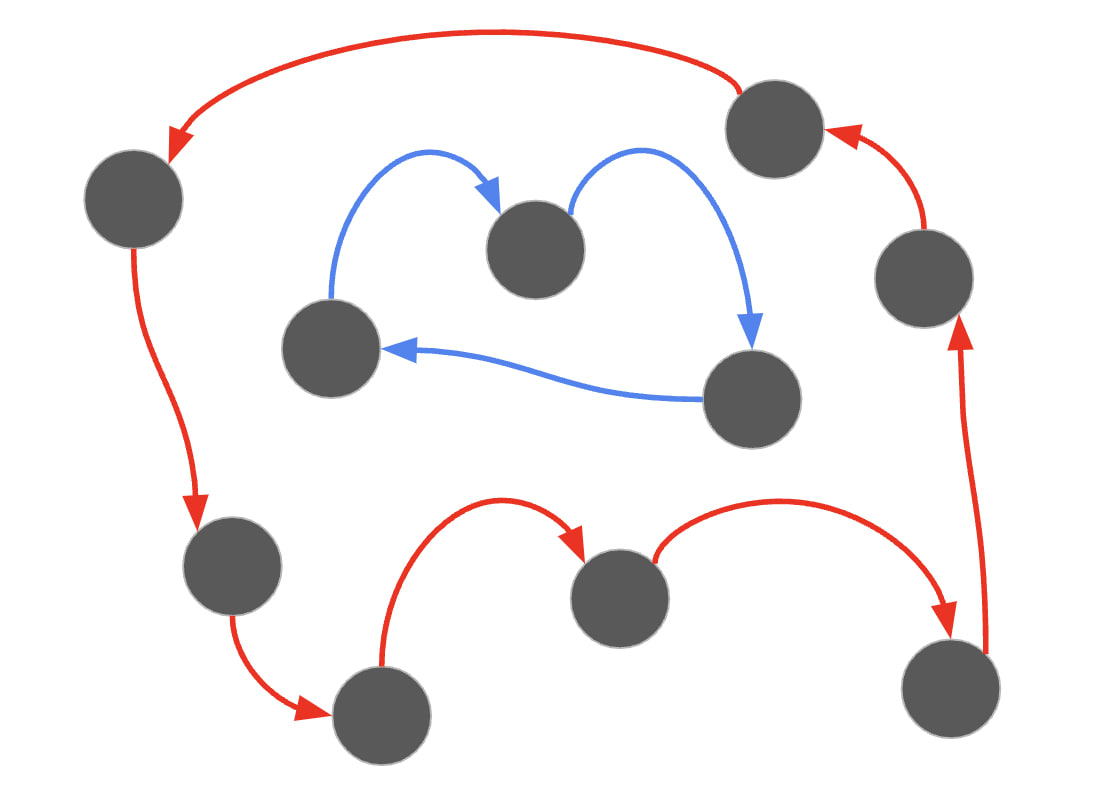
部分巡回路が残ってしまっている例。このようなルートではセールスマンが二人必要になるのでNG

ポテンシャル定式化

では、巡回セールスマン問題を修正してみましょう。まずは1つ目の違い、しりとり問題は巡回路ではありません。これにたいする対処は簡単で、ダミーのタイトルを用意して、そこを通っているものとみなせば良さそうです。

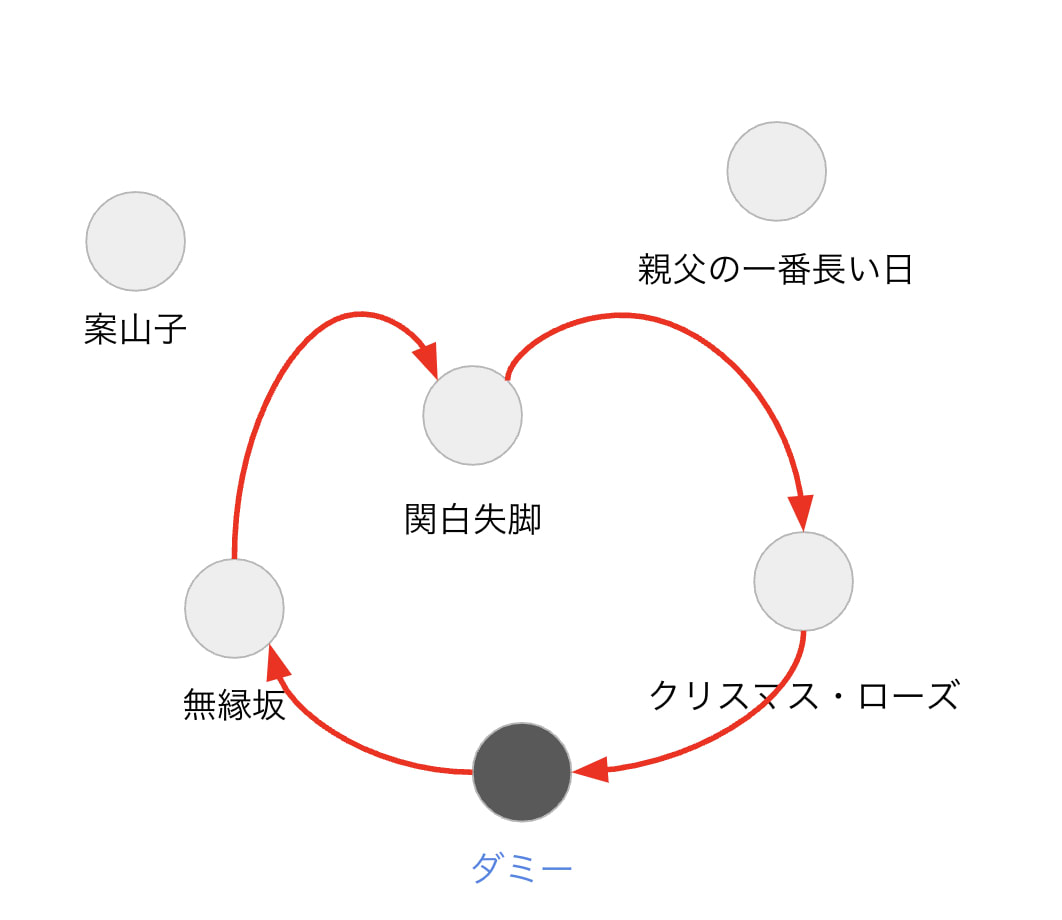
ダミーを通っているものとすれば巡回路とみなせる

そこで、添字を以下のように使い分けることとします

$i,j$ : タイトルを表す添字
$I,J$ : タイトルもしくはダミーのタイトルを表す添字

また、しりとりになっている組み合わせの集合を $C$ とします

$C$ : しりとりになっているタイトルの組み合わせ集合
- $(i, j)\in C$ であればタイトル $i$ からタイトル $j$ にしりとりでつながる（タイトル $i$ の語尾がタイトル $j$ の頭文字になっている）

目的関数

目的関数は、単純につなげられた個数です。これは以下のように書けます。

\max \sum_{ij}{x_{ij}}

制約条件

全てのタイトルを回る必要がないことを考えると、以下のようになります。

$\sum_{J} x_{JI} \leq 1 \quad \mathrm{for}\ \forall I$
- 各タイトルは最大1回だけ利用可能
$\sum_{J}x_{IJ} \leq 1 \quad \mathrm{for}\ \forall I$
- つづくタイトルは1つだけ
$z_{I} + 1 - N(1 - x_{Ij}) \leq z_{j}\ \forall I,\ j$
- 部分巡回路除去
$x_{i,j} = 0 \ \forall (i, j) \notin C$
- しりとりになっている（しりとりにならない経路は利用できない）

実装

今回は実装に PuLP を利用しました。

定式化部分のコード

import pulp
import numpy as np
import pandas as pd

...

# data は title, prefix, suffix 列をもつデータフレーム
data = load_data(path)

# 問題を定義。最大化。
problem = pulp.LpProblem('さだまさしでしりとり', sense=pulp.const.LpMaximize)

# タイトル数
n_titles = len(data)
# ダミータイトル分を追加
indices = range(n_titles + 1)
# 最後に追加したものがダミー
dummy_index = n_titles

# ポテンシャルの定義
z = np.array(
    pulp.LpVariable.matrix(
        'z',
        indices=(indices,),
        cat=pulp.const.LpContinuous,
        lowBound=0
    )
)

# 変数 x の定義
x = np.array(
    pulp.LpVariable.matrix(
        'x',
        indices=(indices, indices),
        cat=pulp.const.LpBinary
    )
)

# しりとりにならない組み合わせは x[i,j] = 0 として固定
for i in indices:
    for j in indices:
        # ダミーはどのタイトルともつながれる
        if dummy_index in (i, j):
            continue
        # しりとりとなっている条件
        if data.iloc[i]['suffix'] == data.iloc[j]['prefix']:
            continue
        x[i, j].setInitialValue(0)
        x[i, j].fixValue()

# 目的関数。ダミーの分が入っているので -1 している
objective = pulp.lpSum(x) - 1
problem += objective

# 制約条件
for i in indices:
    problem += pulp.lpSum(x[i, :]) == pulp.lpSum(x[:, i])

for i in indices:
    problem += pulp.lpSum(x[i, :]) <= 1

for i in indices:
    for j in indices:
        if j == dummy_index:
            continue
        if i == j:
            continue
        problem += z[i] + 1 - (n_titles + 1)*(1 - x[i, j]) <= z[j]

結果

著者の環境（MacBook Air (M1, 2020), RAM 16G）ではだいたい一分くらいで答えが返ってくるようです。

Result - Optimal solution found

Objective value:                207.00000000
Enumerated nodes:               0
Total iterations:               0
Time (CPU seconds):             46.92
Time (Wallclock seconds):       48.72

Option for printingOptions changed from normal to all
Total time (CPU seconds):       48.64   (Wallclock seconds):       50.60

しりとりの結果

こころとからだ
題名のない愛の唄
立ち止まった素描画
がんばらんばMottto
通りゃんせ
聖夜
椰子の実
岬まで
デイジー
いにしへ
遍路
ローズ・パイ
家路
十六夜
山ざくらのうた
たずねびと
遠い祭
梁山泊
叛乱(クーデター)
雨の夜と淋しい午後は
鉢植えの子供
問題作～意見には個人差があります～
素直になりたくて
天空の村に月が降る
瑠璃光
空蝉
港町十三番地
小さい秋みつけた
旅の宿
鳥辺野
残したい花について
転校生(ちょっとピンボケ)
献灯会
烈
思い出はゆりかご
51
誓いの言葉(Short Version) -立ち直る人々-
東京物語
流星雨
ウェディング・ドレス
水底の町
チャンス
素晴らしき夢
名画座の恋
茨の木
北山杉
霧−ミスト−
とてもちいさなまち
ちからをください
苺ノ唄
たいせつなひと
飛梅
名刺
少年達の樹
緊急事態宣言の夜に
二千一夜
病んだ星
逍遙歌～そぞろ歩けば～
Birthday
いつも君の味方
たくさんのしあわせ
線香花火
微熱
つばめよつばめ
芽生えて、そして
天然色の化石
桐の花
なごり雪
奇跡の人
遠い夏～憧憬～
いのちの理由
鷽替え
驛舎(えき)
木根川橋
詩島唄
黄昏坂
神田川
私は犬に叱られた
退職の日
向日葵の影
GENAH!
南風に吹かれて
天狼星に
理想郷(ニライカナイ)
生きることの1/3
小さな手
掌
LIFE
ふきのとうのうた
建具屋カトーの決心 −儂がジジイになった頃−
6ヶ月の遅刻～マリナ・デル・レイ～
一杯のコーヒーから
落日
つくだ煮の小魚
なつかしい海
道(はないちもんめ)
名もない花
渚にて −センチメンタル・フェスティバル−
手紙
みかんの花咲く丘
案山子
飛沫
木を植えた男 -メイン・テーマ-
ママの一番長い日～美しい朝～
療養所(サナトリウム)
無縁坂
神の恵み～A Day of Providence～
吸殻の風景
抱きしめて
天文学者になればよかった
旅人よ
予約席
きみのふるさと
TOKYO HARBOR LIGHTS
翼をください
生きるものの歌
たとえば
Bye Bye Blue Bird
道化師のソネット
遠くへ行きたい
一期一会
Aじゃないか Eじゃないか -思い上がる人々-
遠い海
みるくは風になった
たまにはいいか
加速度
童話作家
Kana-shimi橋
修二会
絵はがき坂
回転木馬
バニヤン樹に白い月～Lahaina Sunset～
図書館にて
転宅
草枕
ラストレター
仰げば尊し
上海物語
リンドバーグの墓～Charles A.Lindbergh Grave～
不器用な花
夏は来ぬ
ぬけみち
誓いの言葉 -幸福の時-
君は穏やかに春を語れ
恋愛症候群―その発病及び傾向と対策に関する一考察―
つゆのあとさき
君が選んだひと
となりの芝生
ふたつならんだ星～アルビレオ～
October ～リリー・カサブランカ～
空っぽの客席
奇跡～大きな愛のように～
虹の木
きみのとなりに
虹～ヒーロー～
親父の一番長い日
ひき潮
おぼろ月夜
邪馬臺
何もなかった
黄昏アーケード
Dream～愛を忘れない～
茨にもきっと花咲く
胡桃の日
茅蜩
シャボン玉
魔法使いの弟子
肖像画
ガラパゴス携帯電話の歌
短篇小説
償い
祈り
Reborn～嘘つき～
昨日・京・奈良、飛鳥・明後日。
天までとどけ
警戒水位
糸遊
歌紡ぎの小夜曲(セレナーデ)
距離(ディスタンス)
勧酒～さけをすすむ～
むかし子供達は
八月のガーデニア
秋の虹
十三夜
やすらぎ橋
神話
Once Upon a Time
向い風
前夜(桃花鳥)
君の歌うラブソング
偶成
一万年の旅路
時差～蒼空に25¢～
時計
イーハトーヴ
分岐点

単品種フロー定式化

さて、巡回セールスマン問題では、部分巡回路除去の定式化方法によって、求解速度に大きな差が出ることが知られています。最長しりとり問題ではどうでしょうか？ここでは単品種フロー定式化と呼ばれる方法を試してみたいと思います^[3]。

変数

ポテンシャル定式では、部分巡回路除去のために、タイトル $i$ の訪問順を表す $z$ を導入しました。単品種フロー定式化では、タイトルではなく経路 $x_{i,j}$ に順番をつけます。また、タイトル $i$ の利用有無を表す変数 $z$ も用意します。

$f_{i,j} \in \mathbb{N}$ : 経路 $x_{i,j}$ の利用順。利用しない場合は $0$
$z_{i} \in \{0, 1\}$ : タイトル $i$ を利用する場合は $1$ となるフラグ。ポテンシャル定式化の $z_i$ とは別物である点に注意

制約条件

少しテクニカルですが、制約条件は以下の通りです。

$\sum_{J} x_{JI} = z_{I} \quad \mathrm{for}\ \forall I$
- 各タイトルは最大1回だけ利用可能
$\sum_{J}x_{IJ} = z_{I} \quad \mathrm{for}\ \forall I$
- つづくタイトルは1つだけ
$\sum_{J}f_{J,i} + z_{i} = \sum_{K}f_{i,K} \forall i$
- タイトル $i$ への経路と、タイトル $i$ からの経路の順序関係
$f_{I, J} \leq Nx_{I, J}$
- 経路 $(I, J)$ を使わない場合、 $f_{I, J} = 0$
$x_{i,j} = 0 \ \forall (i, j) \notin C$
- しりとりになっている（しりとりにならない経路は利用できない）

少し補足をすると、 $\sum_{J}f_{J,i}$ の $f_{J,i}$ は、どれか1つだけが $０$ でない値をもっています。よって、 $\sum_{J}f_{J,i}$ はまさに $0$ でない $f_{J,i}$ の値と等しくなります。これは別のタイトルからタイトル $i$ への経路の使用順、つまりタイトル $i$ の順番を表しています。同様に $\sum_{K}f_{i,K}$ は、タイトル $i$ から出ていく経路の順番を表しています。

実装

短品種フロー定式化のコードは以下の通りです

定式化部分のコード

    problem = pulp.LpProblem('さだまさしでしりとり', sense=pulp.const.LpMaximize)

    n_titles = len(data)
    indices = range(n_titles + 1)
    dummy_index = n_titles

    # z はタイトルの使用有無なので、Binary
    z = np.array(
        pulp.LpVariable.matrix(
            'z',
            indices=(indices,),
            cat=pulp.const.LpBinary,
        )
    )

    x = np.array(
        pulp.LpVariable.matrix(
            'x',
            indices=(indices, indices),
            cat=pulp.const.LpBinary
        )
    )

    f = np.array(
        pulp.LpVariable.matrix(
            'f',
            indices=(indices, indices),
            cat=pulp.const.LpContinuous,
            lowBound=0,
            upBound=n_titles
        )
    )

    for i in indices:
        for j in indices:
            if dummy_index in (i, j):
                continue
            if data.iloc[i]['suffix'] == data.iloc[j]['prefix']:
                continue
            x[i, j].setInitialValue(0)
            x[i, j].fixValue()
            # x[i, j] == 0 なら、 f[i, j] == 0
            f[i, j].setInitialValue(0)
            f[i, j].fixValue()

    # zにはダミーが含まれている
    objective = pulp.lpSum(z) - 1
    problem += objective

    for i in indices:
        problem += pulp.lpSum(x[i, :]) == z[i]
        problem += pulp.lpSum(x[:, i]) == z[i]

    for i in indices:
        if i != dummy_index:
            problem += pulp.lpSum(f[:, i]) - pulp.lpSum(f[i, :]) == z[i]

    for i in indices:
        for j in indices:
            if i == j:
                continue
            problem += f[i, j] <= (n_titles + 1)*x[i, j]

結果

定式化の工夫により、求解時間が10秒程度まで短縮されました。

Result - Optimal solution found

Objective value:                207.00000000
Enumerated nodes:               0
Total iterations:               0
Time (CPU seconds):             10.61
Time (Wallclock seconds):       11.06

Option for printingOptions changed from normal to all
Total time (CPU seconds):       12.58   (Wallclock seconds):       13.22

しりとりの結果

こころとからだ
誰も知らない二番目のうた
黄昏アーケード
Dream～愛を忘れない～
抱きしめて
天までとどけ
警戒水位
生きることの1/3
ちからをください
一万年の旅路
時差～蒼空に25¢～
遠くへ行きたい
烈
おぼろ月夜
邪馬臺
なつかしい海
岬まで
デイジー
糸遊
ウェディング・ドレス
すろうらいふすとーりー
茨の木
木を植えた男 -メイン・テーマ-
眉山
ママの一番長い日～美しい朝～
療養所(サナトリウム)
息子へ～父からの風～
前夜(桃花鳥)
奇跡の人
東京物語
Reborn～嘘つき～
木根川橋
シャボン玉
まぼろし
白い一日
小さな手
転校生(ちょっとピンボケ)
献灯会
イーハトーヴ
不器用な花
なごり雪
君は穏やかに春を語れ
恋愛症候群―その発病及び傾向と対策に関する一考察―
月の光
流星雨
歌を歌おう
鷽替え
Aじゃないか Eじゃないか -思い上がる人々-
となりの芝生
風が伝えた愛の唄
たまにはいいか
神田川
Once Upon a Time
無縁坂
神の恵み～A Day of Providence～
素晴らしき夢
名刺
心斎橋
精霊流し
交響楽(シンフォニー)
家路
十六夜
病んだ星
少年達の樹
きみのふるさと
遠い夏～憧憬～
いのちの理由
空蝉
道(はないちもんめ)
名もない花
渚にて −センチメンタル・フェスティバル−
天狼星に
二千一夜
山ざくらのうた
黄昏坂
加速度
鳥辺野
残したい花について
天然色の化石
奇跡～大きな愛のように～
理想郷(ニライカナイ)
いつも君の味方
立ち止まった素描画
ガラパゴス携帯電話の歌
たくさんのしあわせ
せっせっせ
聖夜
椰子の実
みるくは風になった
たとえば
Bye Bye Blue Bird
童話作家
帰ろかな
泣クモヨシ笑フモヨシ～小サキ歌ノ小屋ヲ建テ～
天文学者になればよかった
たいせつなひと
遠い海
みかんの花咲く丘
案山子
肖像画
がんばらんば
Birthday
いにしへ
遍路
6ヶ月の遅刻～マリナ・デル・レイ～
一期一会
驛舎(えき)
北山杉
霧−ミスト−
とてもちいさなまち
誓いの言葉 -幸福の時-
緊急事態宣言の夜に
虹の木
桐の花
夏は来ぬ
ぬけみち
小さい秋みつけた
短篇小説
償い
生きるものの歌
旅の宿
道化師のソネット
飛梅
名画座の恋
苺ノ唄
退職の日
向日葵の影
GENAH!
ナイルにて−夢の碑文−
掌
ラストレター
雨の夜と淋しい午後は
破
鉢植えの子供
問題作～意見には個人差があります～
勧酒～さけをすすむ～
むかし子供達は
八月のガーデニア
夢百合草(あるすとろめりあ)
秋の虹
十三夜
やすらぎ橋
しあわせの星
逍遙歌～そぞろ歩けば～
バニヤン樹に白い月～Lahaina Sunset～
図書館にて
転宅
草枕
落日
つくだ煮の小魚
何もなかった
たずねびと
通りゃんせ
線香花火
微熱
つゆのあとさき
木を植えた男(Short Version) -希望の種蒔き-
教室のドン・キホーテ
天空の村に月が降る
瑠璃光
歌紡ぎの小夜曲(セレナーデ)
距離(ディスタンス)
吸殻の風景
茨にもきっと花咲く
胡桃の日
ひき潮
October ～リリー・カサブランカ～
Kana-shimi橋
詩島唄
旅人よ
予約席
きみのとなりに
虹～ヒーロー～
思い出暮らし
神話
私は犬に叱られた
建具屋カトーの決心 −儂がジジイになった頃−
ローズ・パイ
祈り
梁山泊
叛乱(クーデター)
仰げば尊し
飛沫
君の歌うラブソング
偶成
一杯のコーヒーから
LIFE
ふ
ふたつならんだ星～アルビレオ～
親父の一番長い日
茅蜩
修二会
絵はがき坂
空っぽの客席
君が選んだひと
TOKYO HARBOR LIGHTS
つばめよつばめ
芽生えて、そして
手紙
港町十三番地
チャンス
水底の町
誓いの言葉(Short Version) -立ち直る人々-
遠い祭
リンドバーグの墓～Charles A.Lindbergh Grave～
分岐点

まとめ

混合整数計画ソルバーを利用することで、簡単にしりとりをすることができます。次回は、キャラクター数の多さででギネス認定されているあんぱんまんのキャラクターでしりとりをするかもしれません。

数理最適化は実務では結構硬いお題をとくことが多いです。もうちょっと機械学習のようにキャピキャピした例題が増えたほうが普及しやすいかなと思ったので、ゆるめのお題を取り上げてみました。

脚注

今回実装中に同様の取り組みをされている記事をみつけました。「最長しりとりを組合せ最適で解く」も是非ご覧ください。本記事のポテンシャル定式化と同等の定式化をされています。 ↩︎
この $z_{i}$ のことをポテンシャル（物理用語で位置エネルギーのこと）と呼ぶことがあります。 ↩︎
過去に配送計画でいろいろな定式化方法を試してみていますので、興味のある方はこちらも参照ください ↩︎

最長しりとり問題と巡回セールスマン問題

データ準備

巡回セールスマン問題（ポテンシャル定式化）

定数

決定変数

目的関数

制約条件

ポテンシャル定式化

目的関数

制約条件

実装

結果

単品種フロー定式化

変数

制約条件

実装

結果

まとめ

Discussion