[Unity] 論文を読んで紐物理を実装してみよう(XPBD:eXtended Position Based Dynamics)

1. はじめに

今回は別記事にて実装したPBD(Position-Based Dynamics)の改善をしたXPBD(Extended position-Based Dynamics)を論文を読みながら実装してみたいと思います。

論文は以下になります。

https://matthias-research.github.io/pages/publications/XPBD.pdf

本記事は例としてUnityでの実装をしておりますが、論文の内容に関することがメインです。ゲームエンジンに依存した話はありません。以下はUnityのサンプル動画です。最後にGithubのURLを載せています。他にもUE5とGodotのサンプルプロジェクトも用意しておきました。

理解について間違えがある可能性があります。もし解釈に間違えや、筆者が分からないと書いてある部分についてアドバイスなどありましたらコメントして教えていただけると喜びます。

2. PBDとの違い

アルゴリズムに入る前に、まずは「PBDにどのような問題があり、XPBDではどう改善したのか」について抑えたいと思います。まずはAbstractを読んで探っていきたいと思います。

【Abstract】

We address the long-standing problem of iteration count and time step dependent constraint stiffness in position-based dynamics (PBD). We introduce a simple extension to PBD that allows it to accurately and efficiently simulate arbitrary elastic and dissipative energy potentials in an implicit manner.

イテレーション回数と時間ステップが制約剛性に左右されてしまうPBDにおける問題に取り組んだ。任意の弾性とポテンシャルエネルギーの散逸のシミュレーションを正確で効率的にできるようにしたシンプルなPBDの拡張を提案する。

• 制約に使っている剛性がイテレーション回数と時間ステップに左右される
• PBDのシンプルな拡張で解決できた

ということのようです。そのシンプルな拡張についてはここではまだ触れられていないようなので、次の 【1 Introduction】 も読んでみたいと思います。

【1. Introduction】

Our method addresses the problems of iteration and time step dependent stiffness by introducing a new constraint formulation that corresponds to a well-defined concept of elastic potential energy. We derive our method from an implicit time discretization that introduces the concept of a total Lagrange multiplier to PBD.

我々の手法は、弾性ポテンシャルエネルギーの概念が成立するよう定義されている(well-defined) 新しい制約の定式化を導入することで、イテレーションと時間ステップが剛性に依存する問題に取り組んでいる。我々の手法は、ラグランジュ乗数の概念をPBDに導入した陰的離散時間により導出している。

キーワードになりそうな用語が出てきました。それらの詳細はまだよく分かりませんが、分かったことをまとめます。

• 新しい制約の定式化をしたこと
• 「ラグランジュ乗数」というものをPBDに導入していること

「ラグランジュ乗数」が何かも分かりませんし、まだ漠然としていますね。気になるところではありますが、詳細は 【4 Our Method】 できっと分かるのではないかと思います。

【4 Our Method】 にて、PBDの課題を解決したアルゴリズムについて見ていく前に、まずはそのPBDの課題についてもう少し理解を深めたいと思います。その上で、その解決手法について見ていきましょう。

3. PBDの課題

PBDの問題は「制約に使っている剛性がイテレーション回数と時間ステップに左右される」ということでした。「そうなのか」「なぜなのか」を確認してきたいと思います。

■ そうなのか

まずは事実として「そうなのか」に関する記述があるので見てみます。PBDとXPBDのイテレーション回数の違いによる比較がありました。図は論文から引用させていただいております。

引用：Macklin, Miles, Matthias Müller, and Nuttapong Chentanez. "XPBD: position-based simulation of compliant constrained dynamics." Proceedings of the 9th International Conference on Motion in Games. 2016.

上段がPBDで下段がXPBDの図となります。どちらも $k=0.01$ で固定し、左から20, 40, 80, 160回だそうです。PBDはだいぶ回数によって剛性が変わってしまっていますね。

この比較には時間ステップについては記述がありません。あくまでイテレーション回数の問題の比較をしています。

■ なぜなのか

次に「なぜなのか」を確認してきたいと思います。

まずPBDについて思い出してみます。基本の考えは、制約( $C(p) = 0$ )を満たすように、制約距離からのズレを修正しようというものでした。制約を満たすという条件のもとで、どのぐらい移動させていけばいいのかが未知の値です。それを制約を満たす傾き方向へ徐々に近づけていくというニュートン法による繰り返し計算によって解に近い値を求めるという方法でした。

また、剛性を与えるために、シンプルな方法として、この修正のための移動距離に対して剛性 $k$ を掛けていました。つまり、あくまで単純化した方法によるものであり、本来の剛性係数が含まれる弾性力 $F = kx$ に基づいて計算されるものではないと思われます。

直接的に修正移動距離を0.1倍にして、制約を満たす距離まで修正せずにだるんだるんにして剛性を与えています。

関連記述をXPBDの論文から探してみます。

【3 Background】
An undesirable side-effect of simply scaling the position change by $k$ is that the effective constraint stiffness is now dependent on both the time step and the number of constraint projections performed. Muller et al. [2007] attempted to address this by exponential scaling of the stiffness coefficient. However this does not take into account the time step, and does not converge to a well-defined solution in the presence of multiple constraints.

単純に座標変化にて k 倍してしまうことの望ましくない副次効果は、制約剛性が時間ステップと制約射影の実行回数に影響されてしまうことである。 Mullerらは剛性係数の指数スケーリング (exponential scaling of the stiffness coefficient) によりこの問題の対処を試みた。しかし、時間ステップを考慮に入れておらず、複数の制約がある場合に明確な解に収束しない。

ここで言う「剛性係数の指数スケーリング」は前回記事でも触れたイテレーション回数と剛性の話かと思います。これは繰り返し計算時に剛性 $k_i$ をそのままかけてしまうと、変化が非線形になってしまうので、線形にするための工夫についてでした。加工した $k’$ がイテレーション回数だけ掛けられて、最終的には $k$ 倍の結果になる、というものでイテレーション回数を経てちゃんと $k$ 倍になるなら問題ないように思えます。

しかし、単純に座標変化に対して $k$ 倍してしまっているということに変わりはありません。また、その座標変化自体はイテレーションを通してニュートン法で逐次的に更新される値で、拘束を満たすようにする座標変化は数値解析の過程における値であり、物理的に意味のないような経過的な値に $k`$ 倍していっているので、何かしら副作用はあるように思えます。

この部分がおそらくPBDの剛性がイテレーション回数に依存してしまっている問題の原因ではないかと思います。しかし、あまり確証がなく、「これだ！」と明言できないので、さらに調査が必要な部分ではありますが今後の課題にしておき、次に進みます。

■ XPBDでの剛性の扱いについて

ここまでPBDの課題であるイテレーション回数に剛性が影響する理由について調査・考察してきました。

それらを踏まえて、先ほど見た 【1 Introduction】 でもう一度XPBDの記述を思い出してみます。XPBDでは 【1 Introduction】 で述べられているように弾性ポテンシャルエネルギーの概念が成立するような定式を用いて、イテレーションが剛性に依存する問題に対処しているとのことでした。

Our method addresses the problems of iteration and time step dependent stiffness by introducing a new constraint formulation that corresponds to a well-defined concept of elastic potential energy.

我々の手法は、弾性ポテンシャルエネルギーの概念が成立するよう定義されている(well-defined) 新しい制約の定式化を導入することで、イテレーションと時間ステップが剛性に依存する問題に取り組んでいる。

おそらくPBDのように「制約を満たすようにする修正移動距離に対して $k$ 倍して剛性をコントロール」するのではなく、制約距離からのズレにかかる弾性力 $F=kx$ を考え、その弾性力による拘束のポテンシャルエネルギーに関する式を解いて位置を修正していると思われます。

■ PBDの課題についてまとめ

まとめます。

• イテレーション回数によってPBDの剛性が変化することを論文から読み取った
• なぜPBDはイテレーション回数に影響されるのか考察した
• XPBDは剛性係数 $k$ の使い方がPBDとは異なるのではないか、と論文の記述から読み取った

では、次は実際にXPBDの手法について読み進めていきたいと思います。ここで考察した剛性係数 $k$ の扱いについても着目していきたいと思います。

4. XPBDの手法について読んでいく

4.1. アルゴリズムの概要

アルゴリズムを見てみると、冒頭でも触れたラグランジュ乗数 $\lambda$ を用いています。ラグランジュ乗数に関する行だけハイライトしました。ざっくり雰囲気だけ見ると、イテレーションの中で式 $(18), (17)$ を解き、 $x$ を更新しています。

実装だけであれば、このアルゴリズムと示された式さえあればできそうです。ただ、どういう仕組みで解いているのかに関心があるのでそこを丁寧に論文から探っていきたいと思います。

引用：Macklin, Miles, Matthias Müller, and Nuttapong Chentanez. "XPBD: position-based simulation of compliant constrained dynamics." Proceedings of the 9th International Conference on Motion in Games. 2016.

4.2. ポテンシャルエネルギーから運動方程式を立てる

論文を読んでいく前に、前回のPBDの記事にて、制約関数ポテンシャルエネルギーやそれを微分することで力が計算できることについて説明をしています。以降はそれを前提に説明をしたいと思います。
https://zenn.dev/nrdev/articles/141dbc5774f666

先に論文の全体像を述べておくと、PBDでは扱わなかった運動方程式から始めていき、制約条件の式なども入れて方程式を解いていきます。運動方程式といえば $F=ma$ の式でした。つまり「質点に作用する力」と「その力による加速度」に関しての式です。

ではどのような力について考えているのか。PBDでは制約関数 $C(x)$ を定義します。この制約関数 $C(x)$ の例としては「距離」制約です。決め方によりますが「2点間の距離が $1cm$ である」のような制約です。制約を満たしている状態では $C(x_1, x_2) = 0$ となります。では、2点( $x_1$ と $x_2$ )がズレて $1.5cm$ になってしまったとします。この時、制約関数 $C(x_1, x_2)$ は制約 $1cm$ からのズレ $0.5$ を返します。制約から外れると その「外れ距離」に応じたバネのような弾性力 を加えて、初期の安定した制約距離に戻します。このように 制約を満たすような状態にするような力を考えて運動方程式を立てて います。

また、重要な点としては、まず弾性ポテンシャルエネルギーを考え、 それを微分することで弾性力が計算 できます。この辺りの詳細は前回の記事に任せます。

問題を解く上で弾性力を直接使わず、ポテンシャルエネルギーを扱います。調べたところ、解析力学では定義が座標に依存しないよう一般化するためにポテンシャルエネルギーを用いて、運動方程式と同じような関係式であるラグランジュ方程式を使ったりするようです。込み入った話になりそうだったので 「ポテンシャルエネルギーを微分したら力が計算できる」 という点だけ記憶に留めて進めていきたいと思います。

それでは 【4 Out Method】 を読んでいきます。

We derive our extended position-based dynamics algorithm (XPBD) by starting with Newton’s equations of motion subject to forces derived from an energy potential $U(x)$:

$$\bold{M} \ddot{\bold{x}} = -\nabla U^{T}(\bold{x}) \tag{3}$$

ポテンシャルエネルギー $U(x)$ から力を求める力に従うニュートンの運動方程式から始めることで、XPBDアルゴリズムを導出した。

ここで表記に注意します。 $\bold{x}$ は太字になっており、ベクトルを表しています。 $\bold{x} = [x_1, x_2, \dots, x_n]^T$ となっており、各要素 $x_n$ はパーティクルの位置です。

もう一つ表記について。 $\ddot{\bold{x}}$ の上の点々は微分を表す表記です。2つあるので $\bold{x}$ の2階微分を表しています。 $\bold{x}$ の2階微分は加速度です。

そして右辺の力は「ポテンシャルエネルギーを微分(勾配)した形」になっていますね。

■ ポテンシャルエネルギー

式 $(3)$ のポテンシャルエネルギー $U(x)$ は、式 $(5)$ に記述されています。

$$U(\bold{x}) = \frac{1}{2}C(\bold{x})^T \alpha^{-1}C(\bold{x}) \tag{5}$$

弾性ポテンシャルエネルギー $\frac{1}{2}kx^2$ の形に近いように見えます。しかし、なんか見慣れない形をしていますね…。しっかりと確認して、これが弾性ポテンシャルエネルギーの式であることを確認していきましょう。

ここでも表記に注意します。 $C(\bold{x}) = [ C_{1}(\bold{x}), C_{2}(\bold{x}), \dots, C_{m}(\bold{x}) ]^T$ というベクトルになっています。個々の制約 $C_m(\bold{x})$ を表すときは添字が付いているので注意です。見慣れなかったのは単にベクトルの入った行列計算の式になっていたからですね。

そして制約関数 $C(\bold{x})$ について、おさらいとして簡単に説明しておきます。 $C_i(\bold{x}) = C_i(x_1, x_2, \dots, x_n)$ という形で、引数のパーティクル座標を計算して制約からのズレの値を返します。PBDの論文では紐のような2点間の制約関数の具体例が示されていました。

$$C_N(p_i, p_j) = \frac{|p_j-p_i| - D_0}{D_0} \\ \begin{aligned} \begin{cases} D_0 &: p_iとp_jの2点間の初期の距離\\ \end{cases} \end{aligned}$$

次に $\alpha ^{-1}$ とはなんでしょうか。

where $\alpha$ is a block diagonal compliance matrix corresponding to inverse stiffness.

$\alpha$ はコンプライアンス (compliance) ブロック対角行列 (a block diagonal matrix) であり、剛性値の逆数と対応している。

ブロック対角行列は対角行列の要素がさらに行列になっているような形式のようです。
https://math-fun.net/20210523/14188/

コンプライアンスは弾性率の逆数のことです。コンプライアンスは法務系で聞きますがそれとは別です。
https://ja.wikipedia.org/wiki/弾性率#弾性コンプライアンス定数

また、対角行列を逆行列にすると、対角成分が逆数になります。
https://risalc.info/src/diagonal-matrix.html

よって、 $\alpha$ は剛性値 $k$ の逆数を成分に持つとのことなので $\alpha^{-1}$ は剛性値 $k$ をそのまま成分に持つ行列となります。なお、ブロック対角行列とのことだったので、下式の $k_m$ はさらに行列を表しているかもしれません。が、ひとまず剛性値が入った行列ということが分かりました。

$$\begin{aligned} \alpha =& \begin{bmatrix} \frac{1}{k_{1}} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & \frac{1}{k_{m}} \end{bmatrix}\\ \\ \alpha^{-1} =& \begin{bmatrix} k_{1} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & k_{m} \end{bmatrix}\\ \end{aligned}$$

これで式中の構成要素は分りました。$U(\bold{x})$の式を具体的に展開してみて、弾性ポテンシャルエネルギー $\frac{1}{2}kx^2$ であるかを確認してみます。各構成要素はベクトルと行列でした。見ていきましょう。具体的に見るために $m=2$ とします。

$$\begin{aligned} U(\bold{x}) &= \frac{1}{2}C(\bold{x})^T \alpha^{-1}C(\bold{x}) \\ &= \frac{1}{2} \begin{bmatrix} C_1(\bold{x}) & C_2(\bold{x}) \end{bmatrix} \begin{bmatrix} k_1 & 0 \\ 0 & k_2 \end{bmatrix} \begin{bmatrix} C_1(\bold{x}) \\ C_2(\bold{x}) \end{bmatrix} \\ &= \frac{1}{2} \begin{bmatrix} C_1(\bold{x}) & C_2(\bold{x}) \end{bmatrix} \begin{bmatrix} k_1 C_1(\bold{x})+ 0 C_2(\bold{x}) \\ 0 C_1(\bold{x}) + k_2 C_2(\bold{x}) \end{bmatrix}\\ &= \frac{1}{2} \begin{bmatrix} C_1(\bold{x}) & C_2(\bold{x}) \end{bmatrix} \begin{bmatrix} k_1 C_1(\bold{x})\\ k_2 C_2(\bold{x}) \end{bmatrix}\\ &= \frac{1}{2} ( k_1 C_1(\bold{x})^2 + k_2 C_2(\bold{x})^2 ) \\ &= \frac{1}{2} k_1 C_1(\bold{x})^2 + \frac{1}{2} k_2 C_2(\bold{x})^2 \\ &\begin{cases} C(\bold{x}) &: 拘束関数をまとめたベクトル。\\ C_j(\bold{x}) &: 拘束関数。スカラー値。\\ \end{cases} \end{aligned}$$

制約関数 $C_{j}(x)$ は「制約距離からのズレ」であり弾性ポテンシャルエネルギー $\frac{1}{2}kx^2$ における $x$ でした。ポテンシャルエネルギー $U(\bold{x})$ の展開後を見てみると、 $\frac{1}{2} k_j C_{j}(\bold{x})^2$ があり、それらの和となっていますね。つまり、各制約のポテンシャルエネルギーの全体合計が $U(\bold{x})$ ということです。 $m=2$ でみましたが仮に $m=1$ としたら $\frac{1}{2}k_1 C_{1}(\bold{x})^2$ となります。

式 $(5)$ の $U(\bold{x})$ は行列で表しているものの、制約(弾性)ポテンシャルエネルギーということが分かりました。行列に慣れている人はすぐに正体が見えているかもしれませんが、分かる範囲で展開してちゃんと正体を確認していきたいと思います。

■ ポテンシャルエネルギーから求める力

メインの運動方程式を再掲します。

$$\bold{M} \ddot{\bold{x}} = -\nabla U^{T}(\bold{x}) \tag{3}$$

力を表している右辺は先ほど確認したポテンシャルエネルギー $U(\bold{x})$ を微分(勾配)して求めています。これは式 $(6)$ に記述されています。

$$\bold{f}_{elastic} = -\nabla_{\bold{x}} U^{T} = -\nabla C^{T} \alpha^{-1} C. \tag{6}$$

これも丁寧に式を見ていきましょう。先ほどの $U(\bold{x})$ の勾配 ($\nabla$) の計算過程を見ていきます。

まず $\nabla$ (ナブラ)の定義を抑えましょう。

https://ja.wikipedia.org/wiki/ナブラ

$$\begin{aligned} \nabla &= \hat{x} \frac{\partial}{\partial x} + \hat{y} \frac{\partial}{\partial y} + \hat{z} \frac{\partial}{\partial z} \\ &= (\frac{\partial}{\partial x}, \frac{\partial}{\partial y}, \frac{\partial}{\partial z}) \\ &\begin{cases} \hat{x} &: x方向の単位ベクトル。yzについても同様。 \end{cases} \end{aligned}$$

各 $xyz$ の単位ベクトルの項の和になっています。 $\frac{\partial}{\partial x}$ は偏微分をするような 演算 を表しています。ベクトル表記にすると式の2行目のように各成分に対して偏微分を行うような演算になります。つまりは この演算の結果はベクトル になります。Wikipediaの説明に「スカラー場の勾配」とありますが、 $U(\bold{x})$ も $C(\bold{x})$ も座標 $\bold{x}$ によって値が決まるスカラー場でした。よって $\nabla U(\bold{x})^T = [\frac{\partial U(\bold{x})}{\partial x} \frac{\partial U(\bold{x})}{\partial y} \frac{\partial U(\bold{x})}{\partial z}]^T$ は「スカラー場の勾配」ベクトルとなります。なので転置の $T$ が書かれています。

あとは関数 $C(\bold{x})$の偏微分が出てくるので、関数の微分についても確認しておきましょう。 $d(f^n) = nf^{n-1}df$ という関係になります。なお、偏微分は多変数のうち1変数を微分することでしたね。

https://ja.wikipedia.org/wiki/関数の微分

では、式 $(6)$ を見ていきます。再掲します。

$$\bold{f}_{elastic} = -\nabla_{\bold{x}} U^{T} = -\nabla C^{T} \alpha^{-1} C. \tag{6}$$

2次の微分をして $\frac{1}{2}$ が消えてたりしてそうで、なんとなーく分かる気もしますが、こちらも丁寧に見ていきましょう。 $U(\bold{x})$ の行列の計算の展開は先ほどやったので省略します。同様に $m = 2$ で見ていきましょう。

$$\begin{aligned} \nabla U(\bold{x})^T &= \nabla (\frac{1}{2}C(\bold{x})^T \alpha^{-1}C(\bold{x})) \\ &= \nabla (上述の式展開なので省略) \\ &= \nabla ( \frac{1}{2} k_1 C_1(\bold{x})^2 + \frac{1}{2} k_2 C_2(\bold{x})^2 ) \\ &= \frac{1}{2} k_1 \nabla C_1(\bold{x})^2 + \frac{1}{2} k_2 \nabla C_2(\bold{x})^2 \\ &= \frac{1}{2} k_1 (2 C_1(\bold{x}) \nabla C_1(\bold{x})) + \frac{1}{2} k_2 (2 C_2(\bold{x}) \nabla C_2(\bold{x})) \\ &= k_1 C_1(\bold{x}) \nabla C_1(\bold{x}) + k_2 C_2(\bold{x}) \nabla C_2(\bold{x}) \\ \end{aligned}$$

これが式 $(6)$ の右辺と一致しているのか、式 $(6)$ の右辺の展開をして確認します。

$$\begin{aligned} \nabla C(\bold{x})^{T} \alpha^{-1} C(\bold{x}) &= \begin{bmatrix} \nabla C_1(\bold{x}) & \nabla C_2(\bold{x}) \end{bmatrix} \begin{bmatrix} k_1 & 0 \\ 0 & k_2 \end{bmatrix} \begin{bmatrix} C_1(\bold{x}) \\ C_2(\bold{x}) \end{bmatrix} \\ &= \begin{bmatrix} \nabla C_1(\bold{x}) & \nabla C_2(\bold{x}) \end{bmatrix} \begin{bmatrix} k_1 C_1(\bold{x})+ 0 C_2(\bold{x}) \\ 0 C_1(\bold{x}) + k_2 C_2(\bold{x}) \end{bmatrix}\\ &= \begin{bmatrix} \nabla C_1(\bold{x}) & \nabla C_2(\bold{x}) \end{bmatrix} \begin{bmatrix} k_1 C_1(\bold{x})\\ k_2 C_2(\bold{x}) \end{bmatrix}\\ &= k_1 C_1(\bold{x}) \nabla C_1(\bold{x}) + k_2 C_2(\bold{x}) \nabla C_2(\bold{x}) \\ \end{aligned}$$

一致しています。予想通りではありますが、 $C_i(\bold{x})^2$ の偏微分なので、そのまま $d(f^n) = nf^{n-1}df$ の形となり、 $2 C_i(\bold{x}) \nabla C_i(\bold{x})$ となりました。微分 $d$ ではなく、$\nabla$ は偏微分かつベクトル形式ですが、やっていることは同じかと思います。

これで式 $(3)$ の運動方程式の右辺の力 $\bold{f}_{elastic} = -\nabla{\bold{x}} U^{T}$ の式の概要が分かりました。制約ポテンシャルエネルギーから運動方程式を立てるところまでは押さえました。

4.3. ラグランジュ乗数

【4.2 ポテンシャルエネルギーから運動方程式を立てる】 ことをしました。次に制約を満たすような位置更新の式を作り、それを解いていきますが、その前に方程式を解く道具である ラグランジュ乗数 について調べたいと思います。話が分断されてしまいますが、ちょっと小難しいので話題を分けて、ラグランジュ乗数のみについてまずは見ていきます。

https://ja.wikipedia.org/wiki/ラグランジュの未定乗数法

ラグランジュの未定乗数法（ラグランジュのみていじょうすうほう、英: method of Lagrange multiplier）とは、束縛条件のもとで最適化を行うための数学（解析学）的な方法である。いくつかの変数に対して、いくつかの関数の値を固定するという束縛条件のもとで、別のある1つの関数の極値を求めるという問題を考える。各束縛条件に対して定数（未定乗数、Lagrange multiplier）を用意し、これらを係数とする線形結合を新しい関数（未定乗数も新たな変数とする）として考えることで、束縛問題を普通の極値問題として解くことができる方法である。

「$g(\bold{x}) = 0$ という束縛条件の下で、目的の関数 $f(\bold{x})$ の極値を求めるという問題」でラグランジュ乗数 $\lambda$ を導入することで問題が解けるという数学的な手法だそうです。束縛条件…！！まさに今扱っている問題ですね！

どんなものかと言うと、以下の式が成り立つというものだそうです。

$$\nabla f(\bold{x}) = \lambda \nabla g(\bold{x})$$

図にして説明してみたいと思います。扱ってるのは3変数ですが、図示するために $x,y$ の2変数関数で説明をします。長々と説明しますが、Wikipediaにもあるような雰囲気をつかむための「幾何的な意味合い」を説明するだけとなります。証明は大変らしいので雰囲気だけ掴み 数式を解くツール として使うに留めておきます。なので、この辺りの文章は飛ばしても大丈夫です。

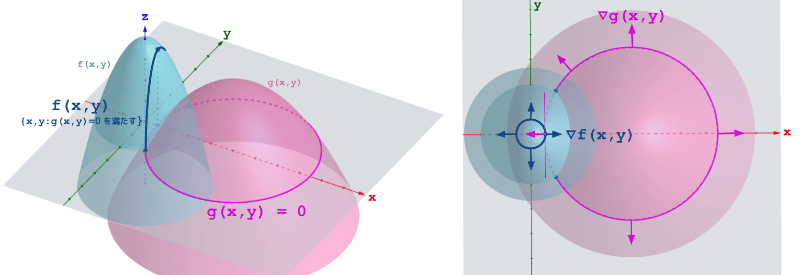
まず、左図のような座標 $(x, y)$ に対して値 $z$ が決まるような関数 $f(x, y)$ を考えます。そして、別の関数 $g(x, y)$ を考え、この関数が $g(x, y) = 0$ であるという制約を与えます。これは左図の赤線上の $(x,y)$ という制約となります。その制約下での $f(x,y)$ の値が左図の濃青線です。(※後述しますが左図とは違い、右図の濃青線は極大値での等高線です。ひとまず気にしないでください。)

つまり $z=0$ の $xy$ 平面上の $g(x,y)$ の曲線を考え、その真上にある $f(x,y)$ の値ということになります。幾何的な2つの式の関係性が分かったと思います。

続いてラグランジュの未定乗数法の等式についてです。2つの式の勾配を計算したときに極値において、向きが平行になっており、スカラー倍の関係になっているというものです。それが右図です。

まず、2変数では勾配 $\nabla = (\frac{\partial}{\partial x}, \frac{\partial}{\partial y})$ となります。傾きですので、 $x$ 方向と $y$ 方向の変位を見た時に $z$ が最も増加するような値となります。例えば右図の $\nabla g(x,y)$ と書いてある矢印線を見てみてください。下に拡大図を用意しました。便宜的に矢印の起点 $(x_{ab}, y_{ab})$ とします。

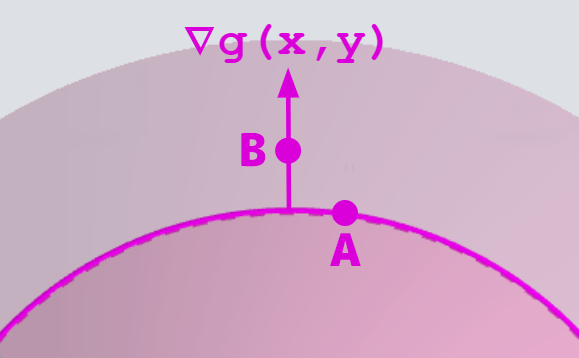
$(x_{ab}, y_{ab})$ を $x$ 方向にのみ動かした点Aを見ます。この円の赤線は $g(x, y) = z= 0$ となる線ですので、この円周上にあるなら $z$ は $0$ のままです。つまり $x$ 方向の傾きは $\frac{0 - 0}{\Delta x}$ でざっくり $0$ となります。ということで $\frac{\partial}{\partial x} g(x_{ab}, y_{ab}) = 0$ です。

次に $(x_{ab}, y_{ab})$ を $y$ 方向にのみ動かした点Bを見ます。$g(x,y)$ は末広がりの円錐形なのでこの地点では $z$ の値は小さくなっています。つまり傾きが発生しています。具体的な値は雑なグラフなのでちょっと分かりませんがなんとなく $-0.3$ ぐらいということにしておきましょうか。 $y$ 方向の傾きは $\frac{(-0.3) - 0}{\Delta y}$ となります。よって、 $\frac{\partial}{\partial y} g(x_{ab}, y_{ab}) = -0.3$ です。

よって、 $\nabla g(x_{ab}, y_{ab}) = (0, -0.3)$ となります。結果、近辺の差分を取ってみたときに、もっとも大きく変化する方向のベクトルとなっています。実は点 $(x_{ab}, y_{ab})$ における $g(x,y)$ の接線と垂直方向となっています。最も変化が大きい方向が接線と垂直な方向です。なので他の場所においても勾配は接線と垂直な方向を示します。

図の矢印の向きについて補足

　すみません、図だと矢印が逆なのでこうですね。ただ、元の図は矢印の描く方向のスペース的な都合で直してません。ここで正しい勾配の向きを図示するだけにしておきます。
 
![](https://storage.googleapis.com/zenn-user-upload/9dbb575ac5a2-20231011.png)

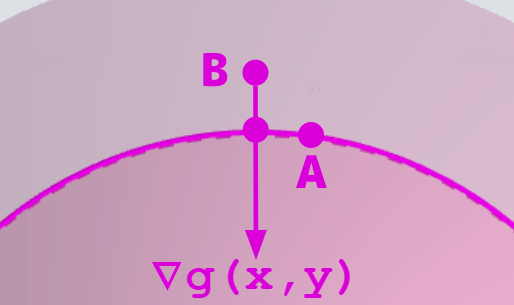
勾配について理解が深まったところで、右図に戻ります。右図は真上から見た図です。こちらも拡大して見てみます。

こちらの濃青線は $f(x,y)$ 側の等高線($z$ の値が同じとなる $(x,y)$ を結んだ線)です。この円の接線を考えます。図のように $f(x,y)$ と $g(x,y)$ の接線が一致する箇所が極値となっているそうです。ただし、 $g(x,y)$ によっては極値が複数ある場合があり、最大・最小が分かるわけではないそうです。

$g(x,y) = 0$ を $xy$ 平面で見たとき、そのグラフは接線方向に移動していきます。その方向が、 $f(x,y)$ において増加があるようなものであれば、まだ極値となるような場所がその増加方向の先にあると考えられます。図のように接線が重なる部分ではそれ以上は $f(x,y)$ の $\Delta (x,y)$ 先で増加はしません。よって極値とみなすことができるのではないかと思われます。しかし、証明までは追えていないので、興味のある方は追ってみるとより身になるかもしれません。

このように接線が一致する場所は以下の式が成り立ちます。傾きベクトルは並行でも向きと大きさは違うので未定乗数 $\lambda$ としています。「極値を取る地点での勾配の関係式」であり、例えば $g(x,y)$ の勾配の大きさが違ってもこの極値を取る場所には影響がなく、関係式は成り立つということかと思います。

$$\nabla f(\bold{x}) = \lambda \nabla g(\bold{x})$$

用意した図が対称性がありシンプル過ぎるので、Wkipediaの図も引用してイメージを深めたいと思います。

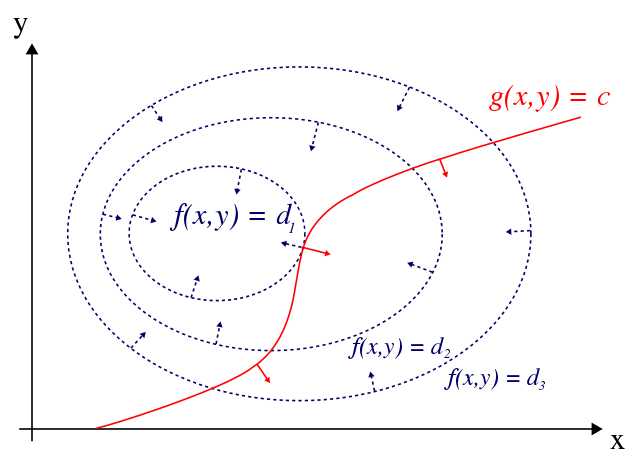
引用：https://en.wikipedia.org/wiki/Lagrange_multiplier

$g(x,y)$ の接線を考えると、極値以外の場所は $f(x,y)$ の山の斜面になっています。その斜面で $f(x,y)$ を微分して斜面の傾きを考えると $f(x,y)$ が増減するので、上か下かまだその先に極値になりそうな場所がありそうで、そんな感じしますね。証明については追いませんが、脳内イメージ的にもそんな感じがします…！！(？) 数学の解説サイトなど探してみると証明などもあるので興味のある人はもっと深堀してみてもいいかもしれません。

次に、この関係式を少し変形します。

$$\begin{aligned} \nabla f(\bold{x}) &= \lambda \nabla g(\bold{x}) \\ \nabla f(\bold{x}) - \lambda \nabla g(\bold{x}) &= 0 \\ \nabla (f(\bold{x}) - \lambda g(\bold{x})) &= 0 \\ \nabla F(\bold{x}, \lambda) &= 0 \\ &\begin{cases} F(\bold{x}, \lambda) = f(\bold{x}) - \lambda g(\bold{x}) とおく \end{cases} \end{aligned}$$

これにより、「別の関数 $g(\bold{x})$ で表される条件が付いた関数 $f(\bold{x})$ の極値問題」を「変数 $\lambda$ が増えたが1つの関数 $F(\bold{x}, \lambda)$ で表され、別の条件関数がない極値問題」に置き換えて考えることができるという手法だそうです。

これで ラグランジュの未定乗数法 についてはおしまいです。着目している関数とその制約関数について、 「スカラー $\lambda$ 倍の違いはあれど勾配が等しい場所が極値になっており、関係式が得られる」というイメージを持って、XPBDに戻りましょう。

4.4. ニュートン法のための式を立てる

ここから特に解法アプローチの解釈を読み解けてるか少し自信がありません…！もし認識が間違っている等ありましたら教えて頂けると嬉しいです。

制約ありの問題にて関係式を立てられるラグランジュの未定乗数法について押さえました。では、元の運動方程式に戻ります。もう一度再掲しておきます。

$$\bold{M} \ddot{\bold{x}} = -\nabla U^{T}(\bold{x}) \tag{3}$$

ここでやりたいことは、 次の時間ステップ $\Delta t$ でも制約を満たすようにしたい ということです。

そして $\Delta t$ 後の値を近似計算できる数学手法にテイラー展開というものがありました。「テイラー展開というのを使うと、未知の関数であってもすごく近くなら微分を使って近似的に値を計算できる」というもので、別記事にて扱いました。

これを使うことでやりたいことの $\Delta t$ 後に関する式を立てることができます。

https://zenn.dev/nrdev/articles/44c5a563846e06

上記の記事では陽解法という「現在の値から未来の値を計算する」というものでシンプルなものでした。XPBDで使う陰解法は「未来の値も式に含んで計算する」というものです。未来の値なんて分からないので、どうやって計算するんだ！という気がしますが、様々な数値計算テクニックを用いて近似的に計算するそうです。なお、未来の値を使うだけあって、陰解法では少し時間ステップ幅が大きくても精度が保たれるそうです。

なので、「近似式を立てる」と「その近似式を数値計算テクニックで解く」を分けて考えていこうと思います。陰解法で未来の値を含んだ「近似式を立てる」ということをしていきます。それが式 $(4)$ で、中心差分法というものを使います。

ここでも表記に注意が必要なのですが、右上の $n$ はべき乗の指数ではなく、時間ステップのインデックスを表しています。 $n$ が時間 $t$ であれば、 $n+1$ は時間 $t + \Delta t$ となります。一応、補足しておきますがこれは $n$ に関してだけで、 $\Delta t^2$ などは通常通り右上は指数です。

$$\bold{M} (\frac{\bold{x}^{n+1} -2\bold{x}^{n} +\bold{x}^{n-1}}{\Delta t^{2}}) = - \nabla U^{T}(\bold{x}^{n+1}). \tag{4}$$

この式 $(4)$ は次のタイムステップにおける式 $(3)$ の加速度 $\ddot{x}$ を2階中心差分法により近似しています。

$$\bold{M} (\ddot{\bold{x}}^{n+1}) = - \nabla U^{T}(\bold{x}^{n+1})$$

$$\begin{aligned} \ddot{\bold{x}}^{n+1} &= \frac{d^2 \bold{x}^{n+1}}{d^2 t} \\ &= \frac{d}{dt} \frac{d \bold{x}^{n+1}}{dt} \\ &= \frac{ \frac{\bold{x}^{n+1} - \bold{x}^{n}}{\Delta t} - \frac{\bold{x}^{n} - \bold{x}^{n-1}}{\Delta t} }{\Delta t} \\ &= \frac{ \bold{x}^{n+1} - 2\bold{x}^{n} + \bold{x}^{n-1} }{\Delta t^{2}} \end{aligned}$$

( $t$ の2階微分なので3行目では分母が $\Delta t$ で分子に1階微分の差がくる)

中心差分については以下の資料を参考として上げ、説明は割愛します。テイラー展開をもとにしており、考え方は前進差分法(オイラー陽解法)と似ています。

http://www.icehap.chiba-u.jp/activity/SS2016/textbook/SS2016_miyoshi_FD.pdf

http://www.damp.tottori-u.ac.jp/~ooshida/edu/ode/g090427.pdf

ひとまずここまでで、式 $(4)$ の変形が分かり、未来の値に関する方程式が得られました。続いて、ラグランジュの未定乗数法を適用して問題を解きます。

ラグランジュの未定乗数法は制約条件を加えつつ $\nabla F(\bold{x}, \lambda) = 0$ という式の問題に変えれました。これをニュートン法によって、この等式を満たすような $\bold{x}$ と $\lambda$ を求めるそうです。

方針は「ラグランジュの未定乗数方を用いて、制約条件付き問題を1つの方程式にすり替え、ニュートン法が使える問題に持っていく」という理解をしています。
理解に自信が無い点 として、どういう極値問題として捉えてラグランジュの未定乗数法を導入しているかです。制約ポテンシャルエネルギー $U(\bold{x}) = \frac{1}{2}k\bold{x}^2$ の運動方程式の値の変化は、力がかからず安定した $\bold{x} = 0$ で $U(0) = 0$ の時になだらかになり、それが極値という感じなのでしょうか。

ニュートン法について抑えておきます。Wikipediaにイメージが分かりやすいgif画像があるのでぜひ一度確認してみてください。傾きを使って反復的に解いていくと $f(x)=0$ となるような $x$ の値を計算できるという手法です。ラグランジュの未定乗数法で得た式は変数が $\bold{x}$ と $\lambda$ の2つがあるので2つの方程式を立てて解いていきます。

https://ja.wikipedia.org/wiki/ニュートン法

論文では割といきなり式 $(7)$ でラグランジュ乗数 $\lambda$ の定義がされて、ニュートン法を解くための2つの方程式 $(8)$ $(9)$ がでてきます。順を追ってこれを見ていきます。

$$\bm{\lambda}_{elastic} = -\tilde{\alpha}^{-1}C(\bold{x}). \tag{7}$$

$$\bold{M}(\bold{x}^{n+1}-\bold{\tilde{x}}) - \nabla C(\bold{x}^{n+1})^{T} \bm{\lambda}^{n+1} = 0 \tag{8}$$

$$C(\bold{x}^{n+1}) + \tilde{\alpha} \bm{\lambda}^{n+1} = 0 \tag{9}$$

それではラグランジュの未定乗数法の出番です。

$$\nabla f(\bold{x}) - \lambda \nabla g(\bold{x}) = 0$$

$f(\bold{x})$ が対象の関数、 $g(\bold{x})$ が対象の関数を制約する関数でした。本問題ではそれぞれ次の式が当てはまると思われます。(後ほど $f(\bold{x})$ 側だけ少し変えます… )

$$\begin{cases} f(\bold{x}) &: U(\bold{x}) = \frac{1}{2}C(\bold{x})^T \alpha^{-1}C(\bold{x}) \\ g(\bold{x}) &: C(\bold{x}) = 0 \\ \end{cases}$$

これをラグランジュの未定乗数法の式に当てはめると次式になります。

$$\nabla U(\bold{x})^{T} - \lambda^{T} \nabla C(\bold{x}) = 0$$

式中の項が $\nabla U(\bold{x}) = \bold{f}_{elastic}$ でそのまま力ですね。置き換えておきます。

$$\bold{f}_{elastic} - \lambda^{T} \nabla C(\bold{x}) = 0$$

力に関する式になっており、運動方程式の式 $(4)$ に若干似ています。どちらも力に関する式なので、 $\bm{\lambda}$ について式を作れます。

式 $(4)$ を変形してこの式の形に持っていき、一部を $\lambda$ と置くことでこの式と一致します。(論文を読み解くために式から変形を探しているので、本来解くためのアプローチの順序はよく分かりませんが…。なのでよく思いつくなぁという気持ちが高まります…。)

$$\bold{M} (\frac{\bold{x}^{n+1} -2\bold{x}^{n} +\bold{x}^{n-1}}{\Delta t^{2}}) = - \nabla U^{T}(\bold{x}^{n+1}). \tag{4}$$

なお、 $\lambda$ を表す式 $(7)$ 、そして式 $(8)$ を見るとまだ説明していない $\tilde{\alpha}$ と $\tilde{\bold{x}}$ が出てきています。これは文中に説明があるので先に説明しておきます。 $\tilde{\alpha}$ は扱いやすくなるよう定数をまとめただけかと思います。 $\tilde{\bold{x}}$ はこれをさらに後ほど別の形に近似置き換えをするのでまとめているのかと思います。

$$\begin{cases} \tilde{\alpha} &= \frac{\alpha}{\Delta t^2} \\ \tilde{\bold{x}} &= 2\bold{x}^{n} - \bold{x}^{n-1} \\ \end{cases}$$

しかし、この $\tilde{\alpha}$ の置き換えをするためにちょっとごにょごにょします。辻褄はあってると思います…。この置き換えのために $\bold{f}_{elastic}$ から $\Delta t^2$ を外に出します。

$$\begin{aligned} \bold{f}_{elastic} &= \bold{M}\frac{\bold{x}^{n+1} - \tilde{\bold{x}}}{\Delta t^2} \\ &= \frac{\bold{f}'_{elastic}}{\Delta t^2} \\ &\begin{cases} \bold{f}'_{elastic} &= \bold{M}(\bold{x}^{n+1} - \tilde{\bold{x}}) \end{cases} \end{aligned}$$

見やすくするため便宜的にこのようにちょっと無理やり外に出してみます。ラグランジュの未定乗数法の式の $\nabla U(\bold{x}) = \bold{f}_{elastic}$ もこの $\bold{f}'_{elastic}$ に置き換えて考えます。式も置き換えて記述しておきます。 ( 式 $(8)$ がそのままこの置き換え後の式がでてきます)

$$\bold{f}'_{elastic} - \lambda^{T} \nabla C(\bold{x}) = 0$$

それでは式 $(4)$ から始めていき、 $\lambda$ を表す式 $(7)$ を求めてみます。なお、 $\bold{f}'_{elastic}$ に置き換えた形から始めます。先に分かりやすいように $\tilde{\alpha}$ も変形しておきたいと思います。

$$\begin{aligned} \tilde{\alpha}^{-1} &= (\frac{\alpha}{\Delta t^2})^{-1} \\ &= (\frac{\Delta t^2}{\alpha}) \\ &= \Delta t^2 (\frac{1}{\alpha}) \\ &= \Delta t^2 \alpha^{-1} \\ \end{aligned}$$

$$\begin{aligned} \frac{\bold{M}(\bold{x}^{n+1} - \tilde{\bold{x}})}{\Delta t^2} &= - \nabla U^{T}(\bold{x}^{n+1}) \\ \frac{\bold{f}'_{elastic}}{\Delta t^2} &= - \nabla C(\bold{x}^{n+1})^{T} \alpha^{-1}C(\bold{x}^{n+1}) \\ \bold{f}'_{elastic} &= \Delta t^2 (- \nabla C(\bold{x}^{n+1})^{T} \alpha^{-1}C(\bold{x}^{n+1}) \\ \bold{f}'_{elastic} &= - \nabla C(\bold{x}^{n+1})^{T} (\Delta t^2 \alpha^{-1})C(\bold{x}^{n+1}) \\ \bold{f}'_{elastic} &= \nabla C(\bold{x}^{n+1})^{T} (-\tilde{\alpha}^{-1} C(\bold{x}^{n+1})) \\ \bold{f}'_{elastic} &= \nabla C(\bold{x}^{n+1})^{T} \bm{\lambda}_{elastic}^{n+1} \\ \bold{f}'_{elastic} &= (\bm{\lambda}^{n+1}_{elastic})^{T} \nabla C(\bold{x}^{n+1}) \\ \bold{f}'_{elastic} - (\bm{\lambda}^{n+1}_{elastic})^{T} \nabla C(\bold{x}^{n+1}) &= 0 \\ \end{aligned}$$

計算の過程で目的の式 $(7)$ の $\bm{\lambda}_{elastic}$ が出てきましたね。なので置き換えて、ラグランジュの未定乗数法の式の形まで持っていきました。最後は $\lambda$ も $\nabla C$ もベクトルで内積になっています。内積は交換法則が成り立つので入れ替えています。

ラグランジュの未定乗数法の式も再掲しておきます。一致していますね。

$$\bold{f}'_{elastic} - \lambda^{T} \nabla C(\bold{x}) = 0$$

これで式 $(7)$ は分かりました。続いて本題の連立方程式である 式 $(8)$ $(9)$ です。が、実はもう出ています…！！この式 $(7)$ と今のラグランジュの未定乗数法の式です！

見ればそのままですが式を見ていきます。まずは式 $(8)$ からです。(最初にさきほど交換法則で入れ替えたのを戻します)

$$\begin{aligned} \bold{f}'_{elastic} - (\bm{\lambda}^{n+1})^{T} \nabla C(\bold{x}^{n+1}) &= 0 \\ \bold{f}'_{elastic} -\nabla C(\bold{x}^{n+1})^{T} \bm{\lambda}^{n+1} &= 0 \\ \bold{M}(\bold{x}^{n+1} - \tilde{\bold{x}}) -\nabla C(\bold{x}^{n+1})^{T} \bm{\lambda}^{n+1} &= 0 \\ \end{aligned}$$

次に式 $(9)$ です。

$$\begin{aligned} \bm{\lambda}^{n+1} &= -\tilde{\alpha}^{-1}C(\bold{x}^{n+1}) \\ \tilde{\alpha}\bm{\lambda}^{n+1} &= \tilde{\alpha}(-\tilde{\alpha}^{-1}C(\bold{x}^{n+1})) \\ \tilde{\alpha}\bm{\lambda}^{n+1} &= - C(\bold{x}^{n+1}) \\ C(\bold{x}^{n+1}) + \tilde{\alpha}\bm{\lambda}^{n+1} &= 0 \\ \end{aligned}$$

この式をニュートン法で解いていきます。ニュートン法の形として見やすいように2変数関数とみなして置いただけだと思いますが、それぞれ式 $(10)$ $(11)$ と置きます。

一応注意書きです。さきほどラグランジュの未定乗数法の説明にて、Wikipediaと揃えて $g(\bold{x})$ と書いていましたが、この式 $(10)$ とは記号かぶりしてしまっておりますが別です。

$$g(\bold{x}, \bm{\lambda}) = 0 \tag{10}$$

$$h(\bold{x}, \bm{\lambda}) = 0 \tag{11}$$

この式らを次のような行列形式の連立方程式にします。なお、 $\bold{K} = \frac{\partial g}{\partial \bold{x}}$ です。

Linearizing equations $(10, 11)$ we obtain the following linear Newton subproblem:

$$\begin{bmatrix} \bold{K} & -\nabla C^{T}(\bold{x}_i) \\ \nabla C(\bold{x}_i) & \tilde{\alpha} \end{bmatrix} \begin{bmatrix} \Delta \bold{x} \\ \Delta \bm{\lambda} \end{bmatrix} = - \begin{bmatrix} g(\bold{x}_i, \bm{\lambda}_i) \\ h(\bold{x}_i, \bm{\lambda}_i) \end{bmatrix} \tag{12}$$

式 $(10, 11)$ を線形化(Linearizing)し、次の線形ニュートン部分問題を得る

$$\begin{bmatrix} \bold{K} & -\nabla C^{T}(\bold{x}_i) \\ \nabla C(\bold{x}_i) & \tilde{\alpha} \end{bmatrix} \begin{bmatrix} \Delta \bold{x} \\ \Delta \bm{\lambda} \end{bmatrix} = - \begin{bmatrix} g(\bold{x}_i, \bm{\lambda}_i) \\ h(\bold{x}_i, \bm{\lambda}_i) \end{bmatrix} \tag{12}$$

ここでいう線形化(Linearizing)とは、1次のテイラー展開により、非線形な式を線形に近似することだと思われます。今回は2変数ですので、まず2変数のテイラー展開について調べておきます。次の通りです。

$$f(x+a, y+b) = f(x,y) + \frac{\partial f}{\partial x}a + \frac{\partial f}{\partial y}b$$

https://eman-physics.net/math/taylor_multi.html

ではまず $g(\bold{x}, \bm{\lambda})$ についてテイラー展開をしてみます。

$$\begin{aligned} g(\bold{x} + \Delta \bold{x}, \bm{\lambda} + \Delta \bm{\lambda}) &= g(\bold{x}, \bm{\lambda}) + \frac{\partial g(\bold{x}, \bm{\lambda})}{\partial \bold{x}}\Delta \bold{x} + \frac{\partial g(\bold{x}, \bm{\lambda})}{\partial \bm{\lambda}}\Delta \bm{\lambda} \end{aligned}$$

式 $(10)$ より、式全体が0になるので次のようにかけます。

$$\begin{aligned} g(\bold{x}, \bm{\lambda}) + \frac{\partial g(\bold{x}, \bm{\lambda})}{\partial \bold{x}}\Delta \bold{x} + \frac{\partial g(\bold{x}, \bm{\lambda})}{\partial \bm{\lambda}}\Delta \bm{\lambda} &= 0 \\ \frac{\partial g(\bold{x}, \bm{\lambda})}{\partial \bold{x}}\Delta \bold{x} + \frac{\partial g(\bold{x}, \bm{\lambda})}{\partial \bm{\lambda}}\Delta \bm{\lambda} &= - g(\bold{x}, \bm{\lambda}) \end{aligned}$$

それぞれの偏微分の式をみていきます。その結果を使って置き換えます。

$$\frac{\partial g(\bold{x}, \bm{\lambda})}{\partial \bold{x}} = \bold{K}$$

$$\begin{aligned} \frac{\partial g(\bold{x}, \bm{\lambda})}{\partial \bm{\lambda}} &= \frac{\partial}{\partial \bm{\lambda}} (\bold{M}(\bold{x}^{n}-\bold{\tilde{x}}) - \nabla C(\bold{x}^{n})^{T} \bm{\lambda}^{n}) \\ &= \frac{\partial}{\partial \bm{\lambda}}( \bold{M}(\bold{x}^{n}-\bold{\tilde{x}})) - \frac{\partial}{\partial \bm{\lambda}}( \nabla C(\bold{x}^{n})^{T} \bm{\lambda}^{n}) \\ &= 0 - \frac{\partial}{\partial \bm{\lambda}}( \nabla C(\bold{x}^{n})^{T} \bm{\lambda}^{n}) \\ &= - \nabla C(\bold{x}^{n})^{T} \\ \end{aligned}$$

それではテイラー展開をした式中の偏微分を置き換えてみます。

$$\begin{aligned} \bold{K} \Delta \bold{x} -\nabla C(\bold{x}^{n})^{T} \Delta \bm{\lambda} &= - g(\bold{x}, \bm{\lambda}) \\ \begin{bmatrix} \bold{K} & -\nabla C(\bold{x}^{n})^{T} \end{bmatrix} \begin{bmatrix} \Delta \bold{x} \\ \Delta \bm{\lambda} \end{bmatrix} &= - g(\bold{x}, \bm{\lambda}) \\ \end{aligned}$$

$g(\bold{x}, \bm{\lambda})$ に関しては式 $(12)$ になりました！
続いて、 $h(\bold{x}, \bm{\lambda})$ についてテイラー展開をしていきます。

$$\begin{aligned} h(\bold{x} + \Delta \bold{x}, \bm{\lambda} + \Delta \bm{\lambda}) &= h(\bold{x}, \bm{\lambda}) + \frac{\partial h(\bold{x}, \bm{\lambda})}{\partial \bold{x}}\Delta \bold{x} + \frac{\partial h(\bold{x}, \bm{\lambda})}{\partial \bm{\lambda}}\Delta \bm{\lambda} \end{aligned}$$

ここまでは同じですね。ではそれぞれの偏微分を見ていきます。

$$h(\bold{x}, \bm{\lambda}) = C(\bold{x}^{n}) + \tilde{\alpha} \bm{\lambda}^{n}$$

$$\begin{aligned} \frac{\partial h(\bold{x}, \bm{\lambda})}{\partial \bold{x}} &= \frac{\partial}{\partial \bold{x}} (C(\bold{x}^{n}) + \tilde{\alpha} \bm{\lambda}^{n}) \\ &= \frac{\partial}{\partial \bold{x}} (C(\bold{x}^{n})) + \frac{\partial}{\partial \bold{x}} (\tilde{\alpha} \bm{\lambda}^{n}) \\ &= \nabla C(\bold{x}^{n}) + 0 \\ &= \nabla C(\bold{x}^{n}) \\ \end{aligned}$$

$$\begin{aligned} \frac{\partial h(\bold{x}, \bm{\lambda})}{\partial \bm{\lambda}} &= \frac{\partial}{\partial \bm{\lambda}} (C(\bold{x}^{n}) + \tilde{\alpha} \bm{\lambda}^{n}) \\ &= \frac{\partial}{\partial \bm{\lambda}} (C(\bold{x}^{n})) + \frac{\partial}{\partial \bm{\lambda}} (\tilde{\alpha} \bm{\lambda}^{n}) \\ &= 0 + \tilde{\alpha} \\ &= \tilde{\alpha} \\ \end{aligned}$$

それではテイラー展開をした式中の偏微分を置き換えます。こちらも式 $(12)$ の形になりました。

$$\begin{aligned} \nabla C(\bold{x}^{n}) \Delta \bold{x} + \tilde{\alpha} \Delta \bm{\lambda} &= - h(\bold{x}, \bm{\lambda}) \\ \begin{bmatrix} \nabla C(\bold{x}^{n}) & \tilde{\alpha} \end{bmatrix} \begin{bmatrix} \Delta \bold{x} \\ \Delta \bm{\lambda} \end{bmatrix} &= - h(\bold{x}, \bm{\lambda}) \\ \end{aligned}$$

これらをまとめて行列で表すと式 $(12)$ になります。再掲しておきます。

$$\begin{bmatrix} \bold{K} & -\nabla C^{T}(\bold{x}_i) \\ \nabla C(\bold{x}_i) & \tilde{\alpha} \end{bmatrix} \begin{bmatrix} \Delta \bold{x} \\ \Delta \bm{\lambda} \end{bmatrix} = - \begin{bmatrix} g(\bold{x}_i, \bm{\lambda}_i) \\ h(\bold{x}_i, \bm{\lambda}_i) \end{bmatrix} \tag{12}$$

ニュートン法は傾きの「方向」に $\Delta \bold{x}$ だけ繰り返し近づけていき、解を得る方法でした。式 $(10), (11)$ をテイラー展開をし、傾き方向への $\Delta \bold{x}$ と $\Delta \bm{\lambda}$ の式を立てました。

この方程式を解き、 $\Delta \bold{x}, \Delta \bm{\lambda}$ を求められれば、次の式 $(13)$ $(14)$ によって、 $\bold{x}$ と $\lambda$ を更新することができます。これを繰り返して行います。そして徐々に解に近づけていきます。(一応補足： $\bold{x}_i$ の $i$ はイテレーションのインデックスです)

$$\bm{\lambda}_{i+1} = \bm{\lambda}_{i} + \Delta \bm{\lambda} \tag{13}$$

$$\bold{x}_{i+1} = \bold{x}_{i} + \Delta \bold{x} \tag{14}$$

なお、論文中にも記述がありますが、ヘッセ行列(Hessian terms)を近似で除外しており準ニュートン法とみなせると書かれています。ニュートン法はヘッセ項という偏微分からなる行列を計算するらしいのですが、大変なので様々な方法で近似して計算するらしくそれを準ニュートン法と呼ぶらしいです。ヘッセ行列や詳細なニュートン法/準ニュートン法について今回はあまり深追いをしませんが、いずれは理解を深めてみたいと思います。

実際に解き始めていきたいところですが、その前に式 $(12)$ をいくつか変更して式 $(15)$ にしています。

$$\bold{K} \approx \bold{M}$$

$$g(\bold{x}_i, \bm{\lambda}_i) = 0$$

$$\begin{bmatrix} \bold{M} & -\nabla C^{T}(\bold{x}_i) \\ \nabla C(\bold{x}_i) & \tilde{\alpha} \end{bmatrix} \begin{bmatrix} \Delta \bold{x} \\ \Delta \bm{\lambda} \end{bmatrix} = - \begin{bmatrix} 0 \\ h(\bold{x}_i, \bm{\lambda}_i) \end{bmatrix} \tag{15}$$

We now introduce two approximations that simplify the implementation of our method and allow us to make a connection back to PBD. First, we use the approximation that $K \approx M$. This omits the geometric stiffness and constraint Hessian terms, and introduces a local error on the order of $O(\Delta t^2)$ .

Next, we assume that $g(\bold{x}_i, \bm{\lambda}_i) = 0$ . This assumption is justified by noting that it is trivially true for the first Newton iteration when initialized with $\bold{x}_0 = \tilde{\bold{x}}$ and $\bm{\lambda}_0 = 0$ . In addition, if the constraint gradients change slowly then it will remain small, and will go to zero when they are constant.

私たちの手法の実装を単純にし、PBDに帰着させるために、2つの近似を導入した。まずは $K \approx M$ の近似をする。これにより剛性と制約ヘッセ項を除外し、 $O(\Delta t^2)$ の局所誤差となる。

次に $g(\bold{x}_i, \bm{\lambda}_i) = 0$ と仮定する。この仮定は次のことに注意することで正当化される。それは $\bold{x}_0 = \tilde{\bold{x}}$ と $\bm{\lambda}_0 = 0$ で初期化し、ニュートン法の初回イテレーションを行うことで自明に成り立つということ。さらに、制約の勾配がゆっくり変化するならば、この値 $g(\bold{x}_i, \bm{\lambda}_i)$ は小さく保たれ、勾配が一定の場合にはゼロに収束する。

ここも理解が怪しいです。 $K \approx M$ に関しては $\bold{K} = \frac{\partial g(\bold{x}, \bm{\lambda})}{\partial \bold{x}}$ を計算すると $\bold{M}$ と剛性と制約ヘッセ項とやらが出てきて、剛性と制約ヘッセ項を無視して $\bold{M}$ だけとみなす、ということなのでしょうか？ヘッセ項については先ほど触れましたが、式変形を試みたもののよく分からなかったです。

次に $g(\bold{x}_i, \bm{\lambda}_i) = 0$ についてですが、こちらも理解があやしいです。式 $(8)$ にて、初回 $\bold{x}_0 = \tilde{\bold{x}}$ と $\bm{\lambda}_0 = 0$ とすると、第1項も第2項も $0$ の積になって、 $0$ になるということでしょうか？ただ、 $g(\bold{x}_i, \bm{\lambda}_i)$ が出てくるのは式 $(12)$ ですし、まだしっかりと咀嚼できていません。

$$\bold{M}(\bold{x}^{n+1}-\bold{\tilde{x}}) - \nabla C(\bold{x}^{n+1})^{T} \bm{\lambda}^{n+1} = 0 \tag{8}$$

近似については理解があやしいですが、ひとまず近似によって式 $(15)$ を得たとして進めたいと思います。

$$\begin{bmatrix} \bold{M} & -\nabla C^{T}(\bold{x}_i) \\ \nabla C(\bold{x}_i) & \tilde{\alpha} \end{bmatrix} \begin{bmatrix} \Delta \bold{x} \\ \Delta \bm{\lambda} \end{bmatrix} = - \begin{bmatrix} 0 \\ h(\bold{x}_i, \bm{\lambda}_i) \end{bmatrix} \tag{15}$$

4.5 実際に解く！

近似をしたことでかなりシンプルになりました。式 $(15)$ から $\Delta \bold{x}$ と $\Delta \bm{\lambda}$ を計算しましょう。まずは $\Delta \bm{\lambda}$ についてです。式 $(15)$ から $\Delta \bm{\lambda}$ について式を立てたのが式 $(16)$ です。

$$\begin{bmatrix} \nabla C(\bold{x}_i) \bold{M}^{-1} \nabla C(\bold{x}_i)^{T} + \tilde{\alpha} \end{bmatrix} \Delta \bm{\lambda} = -C(\bold{x}_i) - \tilde{\alpha} \bm{\lambda}_i. \tag{16}$$

この式には $\Delta \bold{x}$ が含まれていません！！変数は $\Delta \bm{\lambda}$ だけですので、そのまま解くことができます！

$$\Delta \bm{\lambda} = \frac { -C(\bold{x}_i) - \tilde{\alpha} \bm{\lambda}_i } { \nabla C(\bold{x}_i) \bold{M}^{-1} \nabla C(\bold{x}_i)^{T} + \tilde{\alpha} }$$

この式を得るにはシューア補行列(the Schur complement)という数学テクニックを用いています。

https://ja.wikipedia.org/wiki/シューア補行列

$$Matrix := \begin{bmatrix} A & B\\ C & D \end{bmatrix}$$

このようなブロック行列にて $A$ が正則行列であるとき次の式が成り立ちます。

$$Matrix := D - CA^{-1}B$$

よって次のように $\Delta \bold{x}$ を含まずに $\Delta \bm{\lambda}$ だけの式を立てることができます。

$$Matrix \begin{bmatrix} \Delta \bold{x} \\ \Delta \bm{\lambda} \end{bmatrix} = - \begin{bmatrix} 0 \\ h(\bold{x}_i, \bm{\lambda}_i) \end{bmatrix} \tag{15}$$

$$\begin{aligned} Matrix \Delta \bm{\lambda} &= -h(\bold{x}_i, \bm{\lambda}_i)\\ [D - CA^{-1}B] \Delta \bm{\lambda} &= -h(\bold{x}_i, \bm{\lambda}_i)\\ [ (\tilde{\alpha}) - (\nabla C(\bold{x}_i)) (\bold{M}^{-1}) (-\nabla C(\bold{x}_i)^{T}) ] \Delta \bm{\lambda} &= -h(\bold{x}_i, \bm{\lambda}_i)\\ \begin{bmatrix} \nabla C(\bold{x}_i) \bold{M}^{-1} \nabla C(\bold{x}_i)^{T} + \tilde{\alpha} \end{bmatrix} \Delta \bm{\lambda} &= -h(\bold{x}_i, \bm{\lambda}_i)\\ \begin{bmatrix} \nabla C(\bold{x}_i) \bold{M}^{-1} \nabla C(\bold{x}_i)^{T} + \tilde{\alpha} \end{bmatrix} \Delta \bm{\lambda} &= -C(\bold{x}_i) - \tilde{\alpha} \bm{\lambda}_i \end{aligned}$$

これで式 $(16)$ が得られました。

あとは $\Delta \bold{x}$ について解くだけです。 $\Delta \bm{\lambda}$ は計算できたので、こちらにはに $\Delta \bm{\lambda}$ を含んでいても解くことができます。なので愚直に式 $(15)$ から $\Delta \bold{x}$ の式を作ります。それが式 $(17)$ です。

$$\Delta \bold{x} = \bold{M}^{-1} \nabla C(\bold{x}_i)^{T} \Delta \bm{\lambda}. \tag{17}$$

アルゴリズムには式 $(18)$ が示されていましたが、これは単に $\Delta \bm{\lambda}$ の式 $(16)$ を各制約に対して書き直したものです。一応記載しておきますが、形はほぼ式 $(16)$ です。

$$\Delta \bm{\lambda}_j = \frac { -C_j(\bold{x}_i) - \tilde{\alpha}_j \bm{\lambda}_{ij} } { \nabla C_j(\bold{x}_i) \bold{M}^{-1} \nabla C_j(\bold{x}_i)^{T} + \tilde{\alpha}_j }. \tag{18}$$

かなり長くなりましたが以上です！！！！

■ 剛性について

冒頭でPBDの課題について考察しました。そこでXPBDの剛性の扱いについて着目しながら読むと言っていたので最後に触れておきます。

XPBDでは、PBDのように無理やり修正距離を $k$ 倍するのではなく、運動方程式の中に組み込まれて解いています。よって、本来の物理的な剛性として計算され、イテレーション回数に変な依存をしていないのではないかと思います。

5. プログラム

全体のアルゴリズムを再掲します。

引用：Macklin, Miles, Matthias Müller, and Nuttapong Chentanez. "XPBD: position-based simulation of compliant constrained dynamics." Proceedings of the 9th International Conference on Motion in Games. 2016.

以下が実装してみたUnityのコードの抜粋です。極力上記のアルゴリズムと一致するように書いてみました。

void Simulate(float dt)
{
	// x~ = x + Δt v + Δt^2 M^-1 f_ext(x)
	foreach (var (_, p) in _particles)
	{
		// (1): predict position
		var xTilda = p.x + dt * p.v;

		// (3): initialize solve;
		p.xi = xTilda;
	}

	foreach (var c in _constraints)
	{
		// (4): initialize multipliers
		c.λ = 0;
		c.α = _parameter.flexibility;
	}

	// (5)~(13): while
	int i = 0;
	while (i < _parameter.iterations)
	{
		// (6)~(11): for all
		foreach (var c in _constraints)
		{
			// (7): compute Δλ using Eq (18)
			var Δλ = c.ComputeΔλ(dt);
			// (8): compute Δx using Eq (17)
			var Δx = c.ComputeΔx(Δλ);

			// (9): update λ
			c.λ = c.λ + Δλ;
			// (10): update x
			c.p1.xi = c.p1.xi + c.p1.w * Δx;
			c.p2.xi = c.p2.xi - c.p2.w * Δx;
		}
		// (12)
		i = i + 1;
	}

	foreach (var (_, p) in _particles)
	{
		if (p.isFixed) { continue; }
		// (16): update velocity
		p.v = (p.xi - p.x) / dt + _parameter.gravity * dt;
		// (15): update position
		p.x = p.xi;
	}
}

以下は制約ごとに計算している式 $(17)$ $(18)$ です。

class Constraint
{
	// λ = -α~^{-1} C(x) でCに対応
	public float λ;
	public float α;

	public readonly Particle p1;
	public readonly Particle p2;
	public readonly float d;

	public Constraint(Particle p1, Particle p2)
	{
		this.p1 = p1;
		this.p2 = p2;
		d = (p2.x - p1.x).magnitude;
	}

	// Eq (18)
	public float ComputeΔλ(float dt)
	{
		var vector = p2.xi - p1.xi;
		var distance = vector.magnitude;
		var C = distance - d;
		var αTilda = α / (dt * dt);
		var ΔC = vector / distance;
		float invM = p1.w + p2.w;
		return (C - αTilda * λ) / (Vector3.Dot(ΔC, invM * ΔC) + αTilda);
	}

	// Eq (17)
	public Vector3 ComputeΔx(float Δλ)
	{
		var ΔC = (p2.xi - p1.xi).normalized;
		return ΔC * Δλ;
	}
}

5.1. サンプルプロジェクト

動作するUnityプロジェクトはGithubで公開しています。また、UE5とGodotで動作するサンプルも公開しています。

https://github.com/ner-develop/PositionBasedDynamics

https://github.com/ner-develop/PositionBasedDynamicsForUE

https://github.com/ner-develop/PositionBasedDynamicsForGodot

6. さいごに

ところどころまだ理解が浅いところもありますが、どういう手法なのか理解が深まった気がします。一方でヤコビ行列やヘッセ行列、ニュートン法/準ニュートン法などさらに学ぶ必要がありそうなワードがいくつも出てきました。

論文を読んでみるというのはその分野に関する知識がかなり必要だと感じたので、これからも気になる論文を読んで精進していきたいです。PBDの論文読みとは別に、XPBDだけでも実装以外の論文を読み解く部分で1ヵ月ぐらい数式やら英語とにらめっこしていた気がします。数値解析や数理最適(?)などしっかりと触れてこなかった分野を基礎から学びたくなりました。

記事内の指摘や、アドバイス、この分野に関するおススメ書籍や論文などあれば、コメントなどで教えていただけると喜びます！！