📖

[Unity] オイラー陽解法から始める物理シミュ入門

2022/12/15に公開

Unity

物理シミュレーション

tech

はじめに

Unity始めたばかり！という学生さんにも分かるように丁寧に書くよう心掛けました。

前提として 6. プログラムを実装 では実際に物理シミュレーションを試すためにUnityを使ったプログラミングの基本的な知識が必要です。しかし、前半はUnityが分からなくても読めるのではないかと思います。なお、バージョンは Unity2021.3.14f1 を使っています。記事の内容ではバージョン依存はあまりないと思います。

(間違いなどあればご指摘いただけると助かります)

1. 概要

一番簡単で基本らしい 「オイラー陽解法」 をUnityで実装してみる
意味も用法も分からなかった教科書のテイラー展開の実用方法が分かる
「得たい物理の動き」の運動方程式が分かれば、ランタイムでシミュレーション計算して動かせる

いきなり運動方程式と言われても頭がフリーズする人は私を含めて結構多いと思います。
記憶が定かではないですが、高校の物理でやった $F = ma$ です。

「得たい物理の動き」の運動方程式が分かれば

と書いた通り、運動方程式は既に世にある式を用いるので、あまり気負わないでください。あくまで 「道具として物理シミュレーションをする方法」 を説明したいと思います。

しかし、ただ道具としての使い方を説明するだけでなく、その際に用いられるテイラー展開などがどう使われるのか、その数式としての意味について解説し、物理シミュレーションを分かりやすく書ければと思います。

例として実装する振り子

2. 題材とする物理

運動方程式を用いて、その運動の物理シミュレーションをしていきます。
ではまず題材となりそうな運動方程式を探してきます。

振り子の運動方程式 は以下です。これを用いて物理シミュレーションをしていきましょう。

F = ma = -mg \sin \theta \fallingdotseq - \frac{mg}{l}x

ただ、すぐには使わないので振り子の物理シミュレーションをするとだけ念頭において、ひとまず式は忘れて大丈夫です。

3. 少し未来の値を計算する

天気予報だったり、弾道予測だったり、シミュレーションによって未来の値を予測しますね。
今回は、現在時間 $t$ の情報から少し未来の時間 $t + \Delta t$ の情報を計算し、未来の振り子の動きをシミュレーションをしたいわけです。

なお、 $\Delta t$ は時間 $t$ の変化量・差分です。数字が $1 \to 4$ と変われば変化量は $3$ です。 $\Delta t$ という表記を用いて、未来の時間は「現在の時間に少し時間が経過したもの」と書いているだけです。

未来の時間 = 現在時間t + 経過時間\Delta t

さて、未来予知の力を会得してないけど、どうやって未来 $t+\Delta t$ の値を知るの？？？？

昔の数学の天才たちが、未来は分からないけれど特定条件下であれば未来の値が近似によって得られる方法を編み出してくれています。

冒頭で名前を出していますが、それが天才テイラーさんの名を冠した テイラー展開 です。

4. テイラー展開

関数はそのテイラー級数の有限個の項を用いて近似することができる。

点 a を含む実数の開区間 I ⊆ R 上で無限階微分可能な関数 f ∈ C∞(I) が与えられたとき、べき級数
$\sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{k!}(x-a)^{k}$
を関数 f の点 a まわりのテイラー級数という。

...どういうこと？

4.1 そもそも関数 $f(x)$ って？

表記について、少しおさらいをしておきましょう。
$f(x)$ は、なんらかの値 $x$ を渡したときに手に入る値を表しています。関数FunctionのFを取って一般的に $f(x)$ と表記します。
仮に $f(x) = x + 1$ であれば、 $x=1$ を渡せば $f(1) = 1 + 1 = 2$ となります。

プログラムの関数と同じですね。

int f(int x)
{
	return x + 1;
}

4.2 テイラー級数って？

もし数式として関数 $f(x)$ で表現できれば、好きな $x$ を入れることで値が分かるので、未来の値も分かります。高校物理で放物線などを数式で表現して、 $t$ 秒のときの高さを求めたりました。

ですが、複雑な現実の物理においてリアルタイムで速度や力が変わってくる場合には単一の数式で計算することが難しい場合があります。

つまりは 「万能な $f(x)$ なんて分からない！」 のです。

ですが、 $f(x)$ が分からずとも、 ある条件下ではあるものの、その $f(x)$ を近似 し、 $x$ を与えたらそれっぽい値を出してくれる手法を数学の天才が編み出してくれたものがテイラー展開です。

関数はそのテイラー級数の有限個の項を用いて近似することができる。

そして、そのそれっぽい $f(x)$ は以下の数式で近似され得ることができます。

\sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{k!}(x-a)^{k}

魔法のように聞こえますが、まったく未知の $f(x)$ がなんでも分かるというわけではありません。上記の式にあるように $f(x)$ の $n$ 回微分 $f^{(n)}(x)$ が必要だったり、予測できる未来が狭かったり、いろいろ条件はあります。また、ジグザグに不規則なものは微分ができないなどの理由で求められません。

ちなみに上記の式を「テイラー級数」と呼びますが、「級数」というのは単に $A+B+C+D+...$ とたくさん足して求められる数のことです。 $\sum$ を使って表しています。こわもてな記号ですが簡単です。

例は以下です。「 $n$ に $0$ から $5$ を入れて足し合わせた」という式になります。

\sum_{n=0}^{5}n = 0 + 1 + 2 + 3 + 4 + 5

このように、 欲しい $f(x)$ を上述のテイラー級数に展開することをテイラー展開 と呼びます。

4.3 すごい式は分かったが...分からない

もう頭がパンクしそうですが、一言で言えば 「 $x$ を渡すと、正しくはないがそれっぽい近似値が手に入る数式がある」 ということが分かりました。

とはいえ、結局はその数式がよく分からない...。ゆっくり見ていきましょう。

$\sum$ で短く略されてる式を開いてみます。式変形の流れが分かりやすいように細かく書いていきます。

\begin{aligned} f(x) &\fallingdotseq \sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{k!}(x-a)^{k} \\ &= \frac{f^{0}(a)}{0!}(x-a)^{0} + \frac{f^{1}(a)}{1!}(x-a)^{1} + \frac{f^{2}(a)}{2!}(x-a)^{2} + \cdots \\ &= \frac{f(a)}{1}1 + \frac{f'(a)}{1}(x-a) + \frac{f''(a)}{1\times2}(x-a)^{2} + \cdots \\ &= f(a) + f'(a)(x-a) + \frac{f''(a)}{2}(x-a)^{2} + \cdots \end{aligned}

なお、テイラー級数は無限までたくさん足せばとても精度が高くなります。しかし、リアルタイムで計算するには現実的ではないので、今回は精度を犠牲に簡単さを取り、第2項までのとても簡素なものを扱います。

f(x) \fallingdotseq f(a) + f'(a)(x-a)

急にスリムになって寂しくなりました。でも見やすくなりましたね。続きを見ていきましょう。

4.4 ちょっと分かりやすい式になった...分かるかも

f(x) \fallingdotseq f(a) + f'(a)(x-a)

$a$ が謎ですね。まずはテイラー展開のこの $a$ について説明します。

この $a$ はテイラー展開するときに決める定数です。ポップな感じで図示してみました。テイラー展開では、 $a$ を決めて、 そのaの周辺でのみ $f(x)$ を知ることができます。これが 大事な条件 です。好きな未来を知ることはできず、すぐ近くの未来・過去しか知ることができないのです。

$\Delta x = |x - a|$ の範囲がとても小さく、限りなく0に近い時、 $f(x)$ の近似値を得ることができます。上図のかなり狭い青枠の範囲のみです。

\begin{aligned} \Delta x &= x - a \fallingdotseq 0 \\ x &\fallingdotseq a \end{aligned}

ほぼほぼ $x = a$ のような時に限られています。その範囲以外は精度が保証されません。

ただし、テイラー級数の項が多ければその限りではありません。Wikipedia(テイラー展開)で項の数によって、どのぐらいの範囲で、どのぐらい精度が変わるか見れるのでぜひ見てみてください。

以上がテイラー展開の $a$ についての説明です。 $a$ について分かったところで、数式を見ていきましょう。

4.5 やっと未来の値を手に入れる

$\Delta x = x - a$ が限りなく0に近いということを念頭に、数式を置き換えておきましょう。

\begin{aligned} f(x) &\fallingdotseq f(a) + f'(a)(x-a) \\ &\fallingdotseq f(a) + f'(a)\Delta x \end{aligned}

$f(x)$ が手に入りました。では未来の値を手に入れていきます。未来の値は限りなく0に近い $\Delta x$ の範囲で手に入れることができます。なので、関数 $f(x)$ の中に $\Delta x$ だけプラスして少し未来の値を手に入れてみます。

\begin{aligned} f(x+\Delta x) &\fallingdotseq f(a+\Delta x) + f'(a+\Delta x)\Delta x \end{aligned}

式中の $a + \Delta x$ ですが、これは $\Delta x = x - a$ を式変形すれば $x$ になります。

\begin{aligned} \Delta x = x - a \\ \Delta x + a = x \end{aligned}

では、これで式中の $a + \Delta x$ を置き換えてみましょう。

\begin{aligned} f(x+\Delta x) &\fallingdotseq f(a+\Delta x) + f'(a+\Delta x)\Delta x \\ &\fallingdotseq f(x) + f'(x)\Delta x \end{aligned}

とても分かりやすい式になりましたね！！

\begin{aligned} f(x+\Delta x) &\fallingdotseq f(x) + f'(x)\Delta x \end{aligned}

つまり、 $\Delta x$ だけ未来の値は 「現在の値 + 現在の微分値 × $\Delta x$ 」 で求められます。

簡単な数式 $f(x) = x^2$ で考えてみると分かりやすいかと思います。下図に $f(x) = x^2$ の拡大図を示しました。ある $a$ での微分値 $f'(a)$ は $a$ における傾きになります。 $\Delta x$ のすごく小さい範囲を見ると、 「現在の値 + 現在の微分値 × $\Delta x$ 」 が当てはまっていそうです。

\begin{aligned} f(a+\Delta x) &\fallingdotseq f(a) + f'(a)\Delta x \\ &\fallingdotseq f(a) + \frac{\Delta y}{\Delta x}\Delta x \\ &\fallingdotseq f(a) + \Delta y \end{aligned}

$f(x) = x^2$ グラフの拡大図

4.6 テイラー展開のまとめ

少し先の未来の値を近似式によって計算できる
$f(x)$ 自体は分からなくても、ある時点 $a$ における値 $f(a)$ とその微分 $f'(a)$ が分かればいい

5. 振り子の動きをシミュレーションしよう

やっと本題です。長かったですが、少し先の未来の値をテイラー展開を使って計算する雰囲気が掴めたでしょうか。近似式の $x$ を時間 $t$ にリネームして再掲します。

f(t+\Delta t) \fallingdotseq f(t) + f'(t)\Delta t

5.1 振り子の座標を計算する

続いて、振り子の動きを思い出しておきましょう。

振り子の座標を動かしたいので、座標について考えます。 $\Delta t$ だけ経過した未来の座標を計算をしたいです。なお、座標だと分かりやすいように $f(t)$ はPositionのPを取って $p(t)$ と置き換えておきます。

p(t+\Delta t) \fallingdotseq p(t) + p'(t)\Delta t

未来の座標p(t+\Delta t) = 現在の座標p(t) + 座標の時間微分p'(t) \times \Delta t

ですね。座標の時間微分 $p'(t)$ とはなんでしょうか。(座標の時間微分だと語弊がありそうなので、移動座標の時間微分と言うべきかもしれません)

そもそも微分とはなんだったでしょうか。(Wikipedia(微分))

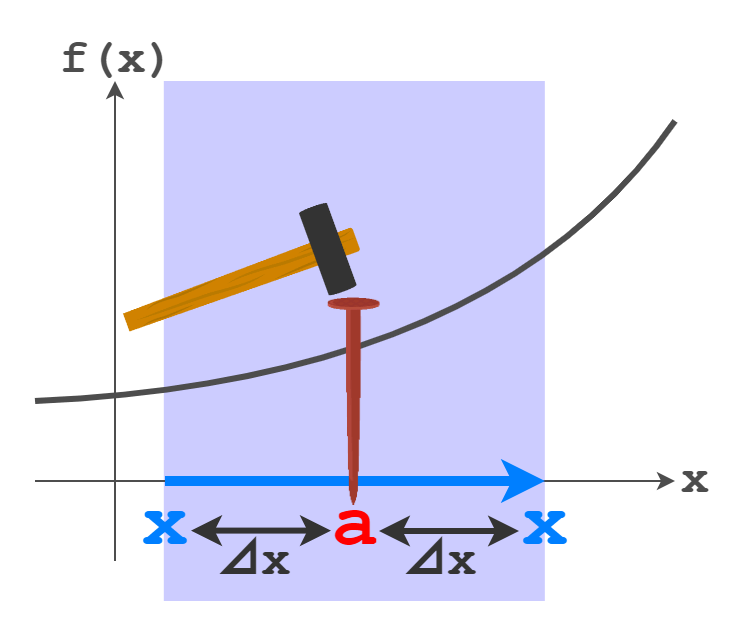
下図のように、 $\Delta x$ だけ進んだら $\Delta y$ がどれだけになるかという2点間を見た時の $f(x)$ の変化量です。ただし、 $\Delta x$ を限りなく0に近づけた極限を取り、2点間ではなく実質1点における $\Delta t$ 経過後の $f(x)$ の変化量を求めるものです。

つまり、座標の時間微分とは 「極短い時間 $\Delta t$ でどれだけ座標が移動するか」 です。言ってしまえば速度です。速度の単位は $m/s$ で分母に時間、分子に距離となっており、微分の $\lim_{\Delta t \to 0}\frac{\Delta position}{\Delta t}$ とも単位としては一致します。

よって、式は次のようになります。なお、時刻tにおける速度はVelocityのVをとって $v(t)$ と表記しておきます。

未来の座標p(t+\Delta t) = 現在の座標p(t) + 現在の速度v(t) \times \Delta t

...これは。見慣れている方もいそうです。速度が一定のときの等速直線運動をプログラムで書くときと同じですね。テイラー展開から始まったため難しそうに感じましたが普段から書いている座標計算です。

ただ、振り子の速度が分からない上に、振り子は等速直線運動ではないのでまだ計算することはできません。
しかし、あとは速度さえ分かれば計算ができます。

5.2 振り子の速度を計算する

ここでも同様にテイラー展開に頼ります。

v(t+\Delta t) \fallingdotseq v(t) + v'(t)\Delta t

未来の速度v(t+\Delta t) = 現在の速度v(t) + 速度の時間微分v'(t) \times \Delta t

現在の速度 $v(t)$ はよしとして、また微分をなんとかしなければいけません。

速度の時間微分 $v'(t)$ とはなんでしょうか？これも理解すれば簡単な話です。時間微分であれば、 極短い時間 $\Delta t$ にどれだけ速度 $v(t)$ が変化したか という変化量が速度の時間微分です。

そう、加速度です！！また単位を見てみましょう。加速度の単位は $m/s^2$ です。

\begin{aligned} v'(t) &= \lim_{\Delta t \to 0} \frac{\Delta v}{\Delta t} \\ &= \lim_{\Delta t \to 0} \Delta v \frac{1}{\Delta t} \\ &= \lim_{\Delta t \to 0} (\frac{\Delta position}{\Delta t}) \frac{1}{\Delta t} \\ &= \lim_{\Delta t \to 0} \frac{\Delta position}{\Delta t^2} \\ \end{aligned}

となり、速度の時間微分も $距離 / 時間^2$ となっています。

よって、加速度さえわかればテイラー展開を使って未来の速度が計算できます。

5.3 振り子の加速度を計算する

ここでもまたテイラー展開...だと終わりが見えないですね。もう使わずとも実は手に入ります。 振り子の運動方程式 を思い出してみましょう。

F = ma = -mg \sin \theta \fallingdotseq - \frac{mg}{l}x

ここでの $a$ は加速度です。式変形して $a$ を求めましょう。

\begin{aligned} ma &\fallingdotseq - \frac{mg}{l}x \\ a &\fallingdotseq - \frac{g}{l}x \end{aligned}

現在の座標: $x$ (座標と言っていますが運動方程式にある円弧の長さのこと)
重力加速度の大きさ: $g$
糸の長さ: $l$

これだけで加速度が求められます。そう、最初に出てきた運動方程式 $F=ma$ は加速度 $a$ を求めるのに使うことができるのです。
これでやっと振り子の座標がシミュレーションで計算できそうです。

6. プログラムを実装

6.1 ひな形

順番にコードに落とし込んでいきましょう。まずはひな形を用意しておきましょう。

計算は Time.deltaTime が固定で十分小さいことが保証されている FixedUpdate() で行います。 Update() で Time.deltaTime を取ると、テイラー展開の条件だった $\Delta t$ が限りなく0に近いこと が保証されません。仮に1fpsだった場合、 Time.deltaTime の値は $1$ になってしまいますね。

Update() で計算することもできますが、経過時間分だけ固定 $\Delta t$ で while を使って1frameで数回のシミュレーションを回す必要があります。コードが増えるので、今回は素直に FixedUpdate() を使います。

public class Pendulum : MonoBehaviour
{
	void Start()
	{
	}
	
	void FixedUpdate()
	{
	}
}

6.2 加速度を計算する

加速度、速度、座標の順で計算していけばよいですね。では、まずは加速度 $a$ を計算していきましょう。
加速度は

a \fallingdotseq - \frac{g}{l}x

でした。

public class Pendulum : MonoBehaviour
{
	// t+dt秒の計算をするためにt秒の情報が必要なので、取っておくための変数
	float _x;
	
	void Start()
	{
		// 初期位置をいれておく。開始時の振り子の円弧の長さ。
		_x = 1;
	}
	
	void FixedUpdate()
	{
		// [説明変数] 定数
		float dt = Time.deltaTime;
		float g = Physics.gravity.magnitude;
		float l = 5;
		
		// [説明変数] 現在の値
		float x_t = _x;
		
		// 加速度(速度の時間微分)
		float a = -g / l * x_t;
	}
}

x_t は更新されておらず初期値のままなので、加速度も固定のままです。しかし、最終的に x_t が更新され始めれば、加速度 $a$ も変化していきます。

加速度 $a$ の計算自体は数式のまま1行でとても簡単ですね。

6.3 速度を計算する

加速度 $a$ が計算できたので、続いて速度 $v(t+\Delta t)$ を計算していきます。

v(t+\Delta t) \fallingdotseq v(t) + a\Delta t

public class Pendulum : MonoBehaviour
{
	// t+dt秒の計算をするためにt秒の情報が必要なので、取っておくための変数
	float _x;
	float _v; // <===== NEW
	
	void Start()
	{
		// 初期位置をいれておく。開始時の振り子の円弧の長さ。
		_x = 1;
	}
	
	void FixedUpdate()
	{
		// [説明変数] 定数
		float dt = Time.deltaTime;
		float g = Physics.gravity.magnitude;
		float l = 5;
		
		// [説明変数] 現在の値
		float x_t = _x;
		float v_t = _v; // <===== NEW
		
		// 加速度(速度の時間微分)
		float a = -g / l * x_t;
		
		// dt秒先の速度を計算
		_v = v_t + a * dt; // <===== NEW
	}
}

これまた簡単です。でもまだ座標が更新されていないので正しくないので注意です。次は座標を更新していきましょう。

6.4 座標...、振り子の円弧の長さ $x$ を計算する

やっと最後です！！ここまでくると次の座標 $p(t+\Delta t)$ も簡単そうですね。

p(t+\Delta t) \fallingdotseq p(t) + p'(t)\Delta t

ただ、今回は 振り子の円弧の長さx について考えているので、 $x(t+\Delta t)$ と書き直しておきます。ただのリネームで深い意味はありません。

x(t+\Delta t) \fallingdotseq x(t) + v(t)\Delta t

public class Pendulum : MonoBehaviour
{
	// t+dt秒の計算をするためにt秒の情報が必要なので、取っておくための変数
	float _x;
	float _v;
	
	void Start()
	{
		// 初期位置をいれておく。開始時の振り子の円弧の長さ。
		_x = 1;
	}
	
	void FixedUpdate()
	{
		// [説明変数] 定数
		float dt = Time.deltaTime;
		float g = Physics.gravity.magnitude;
		float l = 5;
		
		// [説明変数] 現在の値
		float x_t = _x;
		float v_t = _v;
		
		// 加速度(速度の時間微分)
		float a = -g / l * x_t;
		
		// dt秒先の速度を計算
		_v = v_t + a * dt;
		
		// dt秒先の座標を計算
		_x = x_t + v_t * dt; // <===== NEW
	}
}

また一行追加だけです。これで振り子の円弧の長さ $x$ が時間経過によって変動していきます！

7. Unityでシミュレーションを可視化

7.1 Vector3のワールド座標を計算する

実際に球のGameObjectを動かすにはワールド座標 $(x, y, z)$ が必要です。
得られた振り子の円弧の長さ $x$ からワールド座標を計算して、視覚的にシミュレーション結果を見ていきましょう。(細かいですが、便宜的に「長さ」と言っていますが、長さは量であって負の値を持ちません。便宜上、距離のような意味合いで言っており、マイナスの場合は逆方向に振り子が揺れる想定で話しています。)

いろいろ手段はありそうですが、運動方程式に $sin\theta$ がありました。

F = ma = -mg \sin \theta \fallingdotseq - \frac{mg}{l}x

この $sin\theta$ から $\theta$ を計算し、球の初期位置から $\theta$ だけ回転ささせて計算することにします。

回転はクォータニオンを使います。Quaternion.AngleAxis() を使うことで軸を指定して、好きな角度だけ回転するようなクォータニオンを手に入れられます。なので、振り子の支点を軸として $\theta$ を渡して回転させます。

物理シミュレーションで得た 振り子の円弧の長さ $x$ の確認のためのコードなので、申し訳ないですがクォータニオンとは何かなどの説明は省かせていただきます。

また、非常に申し訳ないですが、 $sin\theta$ から $\theta$ を計算する方法についても別の数学の知識が必要になるので本記事では省かせていただきます。

必要であれば追記するか、別記事に補足として書きたいと思います。

Vector3 CalcBallPosition(float x, float l)
{
	// 円弧の長さが分かっても座標が分からないので、運動方程式にあったθを求めて座標を計算する
	// F = -m * g * sinΘ ≒ -m * g / l * x
	// sinΘ = x / l
	// Θ = arcsin(x / l)
	float theta = Mathf.Asin(_x / l) * Mathf.Rad2Deg;

	// クォータニオンを用いてθだけ初期位置から回転させる
	var basePosition = l * Vector3.down;
	var swingingPosition = Quaternion.AngleAxis(theta, transform.forward) * basePosition;
	return swingingPosition;
}

7.2 可視化する

先ほど定義したメソッドで 振り子の円弧の長さ $x$ から座標を計算します。
デフォルトの球体のGameObjectの座標をこれで更新します。

また、振り子なので紐が欲しいですね。自分で動的Mesh生成してもよいですが、Unityには LineRenderer というコンポーネントがあり、今回はこれで十分なので使わせてもらいます。

それらを加えた最終的なコードは以下になります。

using UnityEngine;

public class Pendulum : MonoBehaviour
{
	[Header("Components")]
	// 振り子の球
	[SerializeField] Transform _ball;
	// 振り子の紐
	[SerializeField] LineRenderer _line;
	
	[Header("Parameters")]
	// 振り子の紐の長さ
	[SerializeField] float _length = 5;

	// t+dt秒の計算をするためにt秒の情報が必要なので、取っておくための変数
	float _x;
	float _v;

	void Start()
	{
		// 初期位置をいれておく。開始時の振り子の円弧の長さ。
		_x = 1;
	}

	void FixedUpdate()
	{
		// [説明変数] 定数
		float dt = Time.deltaTime;
		float g = Physics.gravity.magnitude;
		float l = _length;
		
		// [説明変数] 現在の値
		float v_t = _v;
		float x_t = _x;
		
		// 加速度(速度の時間微分)
		float a = -g / l * x_t;

		// dt秒先の速度を計算
		_v = v_t + a * dt;

		// dt秒先の座標を計算
		_x = x_t + v_t * dt;

		var swingingPosition = CalcBallPosition(_x, l);
		_ball.localPosition = swingingPosition;

		var lineRootPosition = transform.position;
		_line.SetPositions(new []{lineRootPosition, lineRootPosition + swingingPosition});
	}

	Vector3 CalcBallPosition(float x, float l)
	{
		// 円弧の長さが分かっても座標が分からないので、運動方程式にあったθを求めて座標を計算する
		// F = -m * g * sinΘ ≒ -m * g / l * x
		// sinΘ = x / l
		// Θ = arcsin(x / l)
		float theta = Mathf.Asin(_x / l) * Mathf.Rad2Deg;

		// クォータニオンを用いてθだけ初期位置から回転させる
		var basePosition = l * Vector3.down;
		var swingingPosition = Quaternion.AngleAxis(theta, transform.forward) * basePosition;
		return swingingPosition;
	}
}

実際に動かしてみた様子

8. まとめ

テイラー展開によって、ある $a$ 付近なら未来の値が予測できる
テイラー展開によって、毎フレームで直近の座標を予測し、物理シミュレーションをした

今回はテイラー展開の $1$ 回微分までの項で近似しました。これには名前があり オイラー陽解法 と呼びます。しかし、とても簡単な分だけ問題もあり精度がよくないです。今回作ったプログラムも最初はいいのですが、精度のずれが蓄積して徐々にあらぶってきます。

シンプレクティック法により、簡単な変更で精度が改善したりします。既に文章量が多いので割愛しますが、ほんの少し変更を加えるだけなのでもしかしたら追記するかもしれません。他にも改良オイラー陽解法だったり、他の方法などもあります。

おわりに

今回は振り子のシミュレーションをしました。減速するバネの運動方程式もあるので、衝突時の力から加速度を計算してCubeのScaleを動かしてみると、バウンドする気持ちいい物理的なアニメーションが作れるのではないかと思います。

終盤では、説明を省いてしまったものもいくつかありますが、本題の物理シミュレーション以外で話が膨らむと理解のカロリーが高くなるかと思い割愛させていただきました。

まだ自分自身も勉強中ですので、他の手法などについてもメモ代わりにまた学びながら書いていこうと思います。