点識別可能性と可換図式

この記事では，点識別可能性について，可換図式を使って分かりやすく定義します．

点識別可能とは

点識別可能性の説明

計量経済学には点識別という概念があります．ざっくりいうと，観測可能な変数の分布が分かったとしても，知りたいtarget parameterを一意に特定できない場合，そのtarget parameterは点識別不可能といいます．

詳しくは以下を参照ください．
計量経済学における識別問題について
The Identification zoo

点識別可能性の定義

上記の２つのページの定義は（表面上）若干違うのですが，このページではIdentification zooの定義に従います．

• モデルの集合$MM$
  • DGPとして想定している分布の集合．
• 観測可能な分布について
  • モデルから観測可能な分布への写像$Π:M→Π(M)\Pi: M \to \Pi(M)$
    • モデルが定まれば一意に定まる分布．
  • 観測可能な分布の集合 $Φ=Π(M)\Phi = \Pi(M)$
• target parameterについて
  • モデルからtarget parameterへの写像$Δ:M→Δ(M)\Delta: M \to \Delta(M)$
    • モデルが定まれば一意に定まる値．この値を求めることが目標．
  • target parameterの集合 $Θ=Δ(M)\Theta = \Delta(M)$
• structure $s(ϕ,θ)s(\phi, \theta)$について
  • $s(ϕ,θ)={m∈M:Π(m)=ϕ,Δ(m)=θ}s(\phi, \theta) = \{m \in M: \Pi(m) = \phi, \Delta(m) = \theta \}$
  • つまり，実験者からは$ϕ\phi$として観測され，なおかつ，target parameterが$θ\theta$となる母集団の分布の集合．
• $θ\theta$と$θ′\theta '$が観測同値　$⇔\Leftrightarrow$ $s(ϕ,θ)s(\phi, \theta)$と$s(ϕ,θ′)s(\phi, \theta ')$がともに空ではないような$ϕ\phi$が存在する．
• target parameter $θ\theta$が識別可能 $⇔\Leftrightarrow$ $θ\theta$と$θ′\theta '$が観測同値であれば，$θ=θ′\theta = \theta '$である
  • 要は，実験者からは$ϕ\phi$として観測されるような母集団分布に対しては，同じtarget parameterの値になりますよ，ということ

点識別と可換図式について

点識別の図示

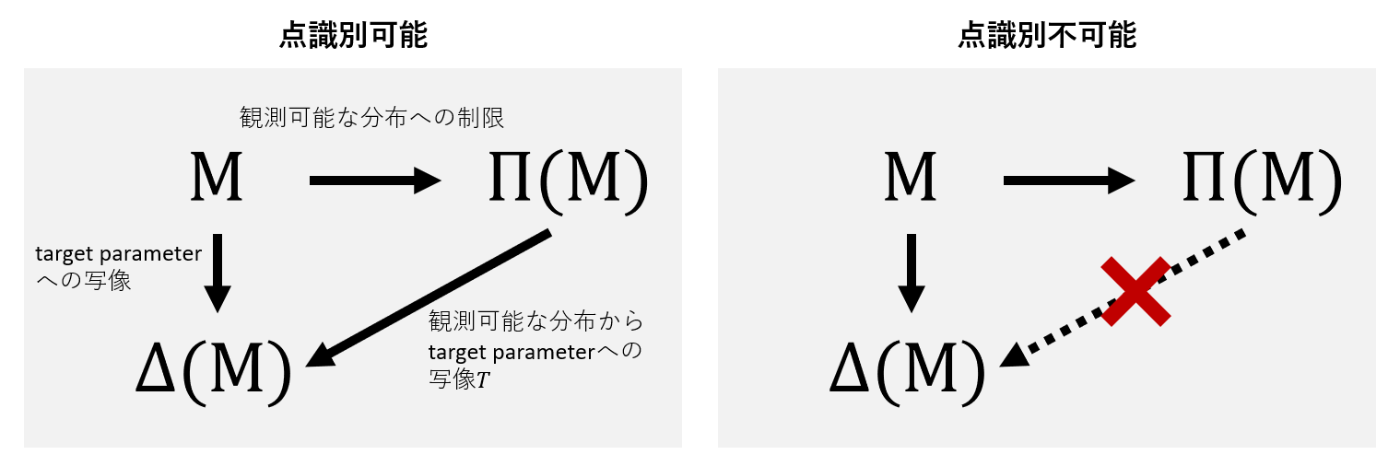
$θ\theta$は識別可能ということは，上のような可換図式が書けるということです．このページで言いたいことはこれだけです．

図示の証明

上記の図を言葉で表現すると以下のようになります．

$θ\theta$は識別可能 $⇔\Leftrightarrow$ 今，$∃T\exist T$が存在して，$Δ(m)=T(Π(m))\Delta(m) = T(\Pi(m))$が存在する

$⇒\Rightarrow$について

背理法を用いる．つまり，ある$θ≠θ′\theta \neq \theta'$について，$s(ϕ,θ)≠∅∧s(ϕ,θ′)≠∅s(\phi, \theta) \neq \emptyset \land s(\phi, \theta ') \neq \emptyset$となる$ϕ\phi$が存在すると仮定する。

この仮定のもとで，$m∈s(ϕ,θ),m′∈s(ϕ,θ′)m \in s(\phi, \theta), m' \in s(\phi, \theta ')$をとることができる．定義より，

• $Δ(m)=θ≠θ′=Δ(m′)\Delta(m) = \theta \neq \theta ' = \Delta(m')$だが，
• $θ=Δ(m)=T(Π(m))=T(ϕ)=T(Π(m′))=Δ(m′)θ′\theta = \Delta(m) = T(\Pi(m)) = T(\phi) = T(\Pi(m')) = \Delta(m') \theta '$なので矛盾．

$⇐\Leftarrow$について

$∀ϕ∈Π(M)\forall \phi \in \Pi(M)$について，$Mϕ={m∣Π(m)=ϕ}M_{\phi} = \{m | \Pi(m) = \phi \}$と定義する．なお，$M(ϕ)M_(\phi)$は空ではない．このとき，$∀m∈Mϕ\forall m \in M_{\phi}$について，$Δ(m)=θϕ\Delta(m) = \theta_{\phi}$（$mm$によらない定数）であれば，$TT$をそのように構築すればよい．

今，ある$ϕ\phi$について，$m≠m′m \neq m'$が存在して，$Δ(m)≠Δ(m′)\Delta(m) \neq \Delta(m')$とする．この時， $s(ϕ,δ(m))≠∅∧s(ϕ,δ(m′))≠∅s(\phi, \delta(m)) \neq \emptyset \land s(\phi, \delta(m')) \neq \emptyset$なので識別可能に矛盾．