[Rust] 自動微分で解く制御問題

今までスクラップで書きためてきた制御問題への自動微分の応用ですが、静的なプロットばかりで面白くないので、リアルタイムシミュレーションを含むインタラクティブな GUI を作りました。

https://github.com/msakuta/rustrol

もちろんブラウザ上で直接動かすことも可能です。

https://msakuta.github.io/rustrol/

デモの一覧

このアプリケーションでは4種類のデモが選べます。右側のパネルで切り替え、またそれぞれのデモのパラメータ調整ができます。

Lunar Lander

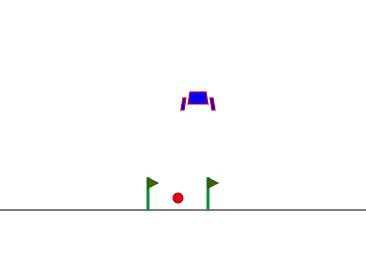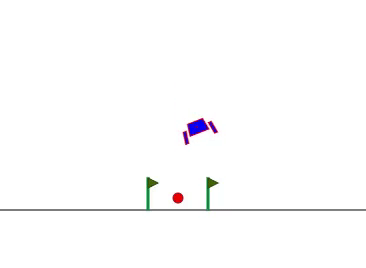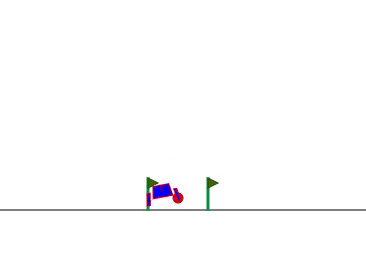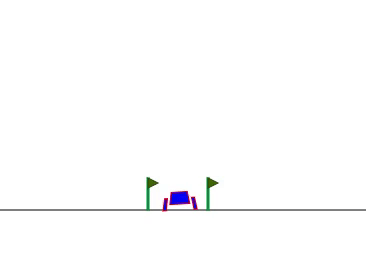
元々は Python で強化学習の実験用プラットフォーム gym (今は gymnasium という名前になっていますが)で登場した問題で、月面着陸船を限られたロケットの向きと推力で静かに着陸させるというものです。

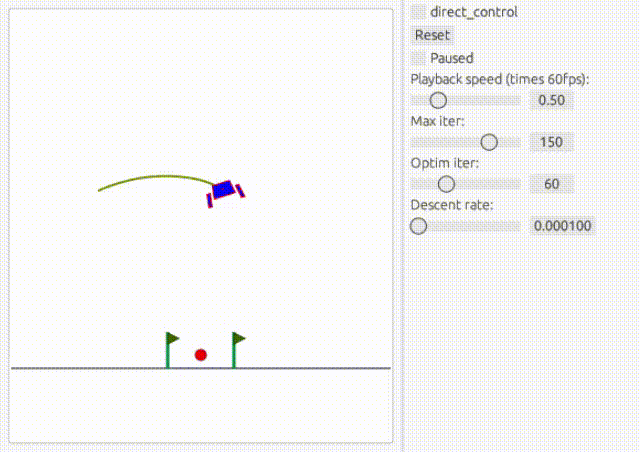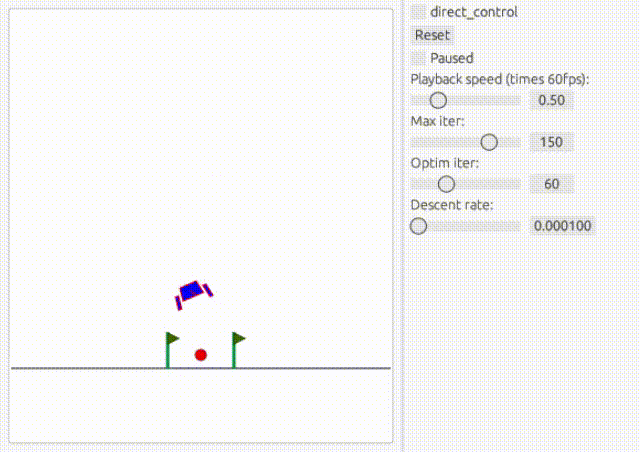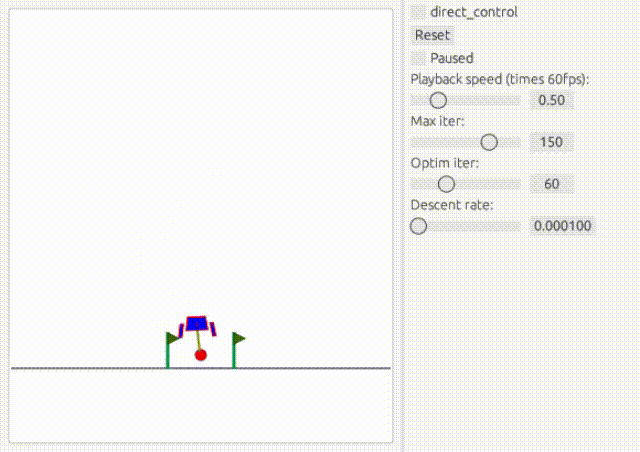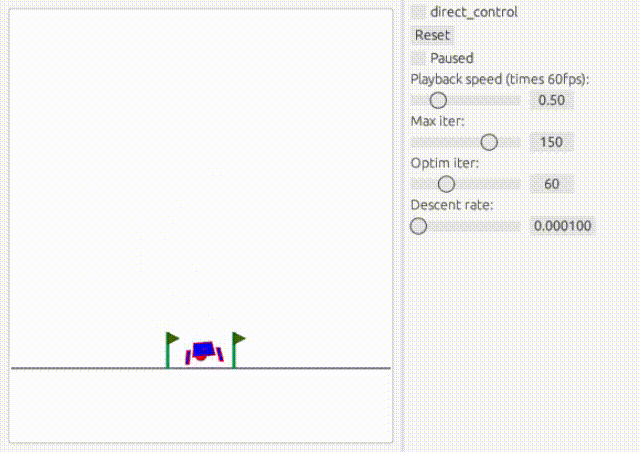
着陸直前はおとなしいですが、前半はあまり乗り心地がよくなさそうです。傾きは大きくなりすぎないように損失関数に傾きの２乗を入れているのですが、なぜか左右に激しく揺れるようで、理由はよくわかりません。

gymnasium のアニメーションではランダムな挙動が初期値として示されています。これを学習させて着陸させるというのがお題です。

ここでは強化学習は使わず、目的地との距離を損失関数とした単純なモデル予測制御 (MPC)^[1]を行います。損失関数から元の制御信号の微分を rustograd の自動微分で求め、再急降下法で最適な入力信号を逐次求めていきます。

この方法の利点は、事前の学習が必要なく、モデルからのシミュレーションと損失関数の定義さえあればそれなりの挙動を示すことです。また、モデルが不完全だったり誤差や観測ノイズが乗っていたとしても、逐次的にそれなりの解に近づいてくれるので、機械学習ベースのアルゴリズムのように過学習を心配することなく、より外乱に強い傾向にあります。

モデル予測制御、あるいは微分係数を使った最適化アルゴリズム全体に共通する弱点としては、初期値によって局所解に陥ってしまう可能性があります。

手動制御

なお、 WASD キーを使った手動制御モードも付けてみました。人間の手で目的地に静かに着陸させるのは相当難しいです。

ミサイル

次のサンプルは、空中の移動体に自機を制御して当てるという問題です。要するに対空ミサイルです。重力下にあるので自機は常に下方向の加速度を受けます。また空気抵抗があり、速度に比例して抵抗が大きくなっていきます。ロケットの加速は自機の向きにしかできず、ロケットの姿勢は変更するのに時間がかかります。このような様々な力のかかるモデルであっても、自動微分を使えばすべてを考慮して勾配を求めることができます。

Moon Lander とのもう一つの違いは、目標も同時に動いていることです。このため最適化プロセスでは予測した各瞬間の目標と自機の距離を求め、その最小値を最小化します。ここでのミソは複数のタイムステップの中での最小値を求めるということです。これが微分可能かというと一見難しそうですが、 rustograd では任意の2変数関数をユーザが定義できるので、次のような "min" 演算を計算グラフのノードとして定義すれば可能です。

pub(crate) struct MinOp;

impl rustograd::BinaryFn<f64> for MinOp {
    fn name(&self) -> String {
        "min".to_string()
    }

    fn f(&self, lhs: f64, rhs: f64) -> f64 {
        lhs.min(rhs)
    }

    fn t(&self, data: f64) -> (f64, f64) {
        (data, data)
    }

    fn grad(&self, lhs: f64, rhs: f64) -> (f64, f64) {
        if lhs < rhs {
            (1., 0.)
        } else {
            (0., 1.)
        }
    }
}

次のアニメーションではランダムに自機の初期位置と速度を変化させて頑健性をチェックしています。

これも一応手動制御の機能を付けたのですが、人間が操作して当てるのは難しすぎて不可能に近いです。難しい原因の一つはキーボード操作でアナログ入力ができないことなので、ジョイスティックか何かを使えばましになるかもしれません。

軌道力学

次のサンプルは、惑星の周りを回る人工衛星の制御問題です。
これは厳密にはモデル予測制御ではなく、目的の天体(他の衛星)とランデブーするための初期速度を求めるという問題です。

次のアニメーションでは、黒い線の円が重力原となる天体(地球など)で、緑の丸が目標天体、青い線が速度の初期値が辿る軌跡、黄土色の線が最適化後の速度が辿る軌跡、紫色の線は目標天体の辿る軌跡、紫色の小さな円は目標と自機の距離が最小になる瞬間です。

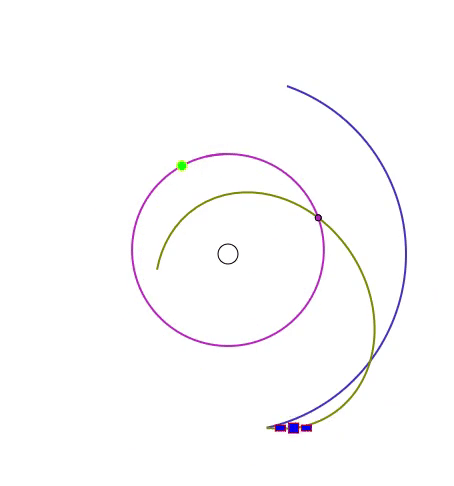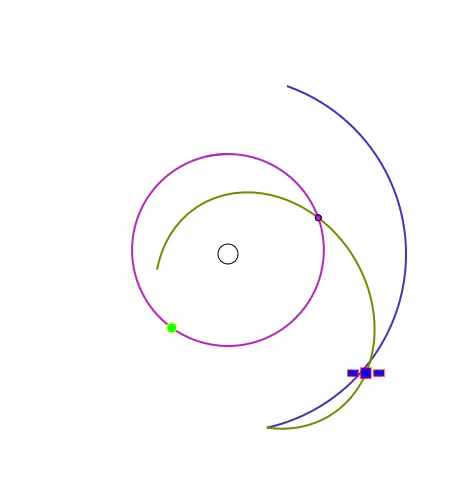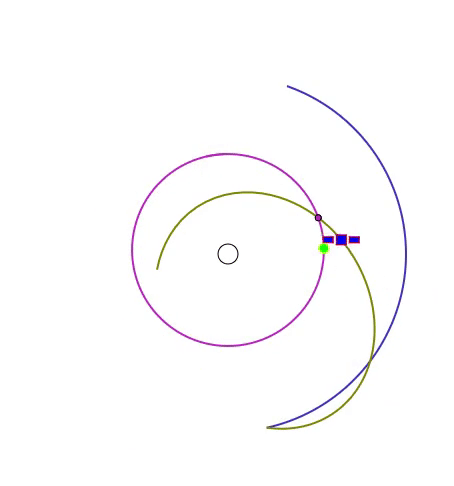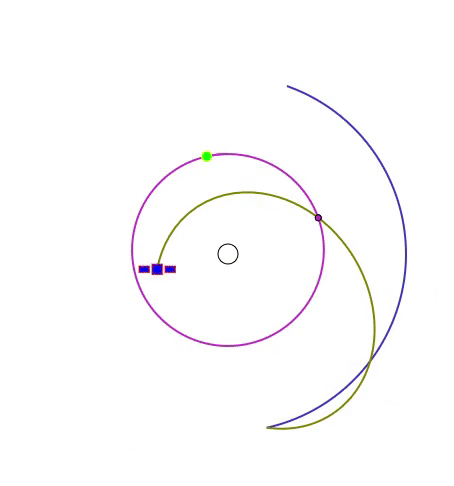
この問題は、今までの2つの問題と異なり、重力場が一様ではないという特徴があります。このため運動方程式のソルバーには2次の Runge-Kutta 法を用いています。

$$\begin{align*} \Delta v_1 &= h f(x) \\ \Delta x_1 &= h v(t) \\ \Delta v_2 &= h f(x + \Delta x_1 / 2) \\ \Delta x_2 &= h (v + \Delta v_1 / 2) \\ v(t+h) &= v(t) + \Delta v_2 \\ x(t+h) &= x(t) + \Delta x_2 \end{align*}$$

ここで $x$ は物体の位置、 $y$ はその速度、 $\Delta$ はシミュレーションステップ間の差分です。 $h$ は離散化時間の差分ですが、ここでは自動微分の式を単純化するために 1 にしています。一つのステップでこれだけの計算があると、全体の式の微分は極めて複雑になります。とても手で計算しようとは思えません。

この問題に関しては、再急降下法で解けるときと解けないときがあります。特に、自機と目標の距離が開始時点で最短である場合、微分係数がゼロになるため、最適解への探索が進みません。このような場合は多数の固定した初期値から最適化を適用し、解空間を探索する必要があります。 rustrol では 3 x 3 のグリッド上の初期値で探索を行い、損失が最も少ないものを採用しています。

三体問題

ニュートンの運動方程式は3体以上の天体が関わると解析的な解を得るのが非常に難しいことが知られています。式で表すのが難しいだけではなく、カオス性があるのがやっかいです。カオス性とは、初期値の非常に小さな差が時間とともに拡大していき、長時間の予測が難しくなる性質です。いわゆるバタフライ効果のような性質です。

このような問題でも、自動微分で目的の軌道に近づくことはできるはずです。ここでは、月からの距離が一定の場合に損失をゼロとし、そこからの差の二乗を損失関数として最適化してみます。理想的には月の周りを安定的に回ってほしいところですが…

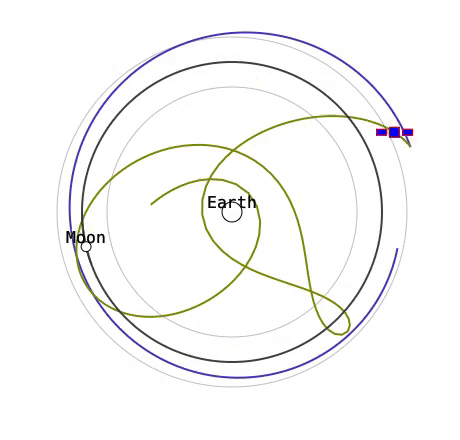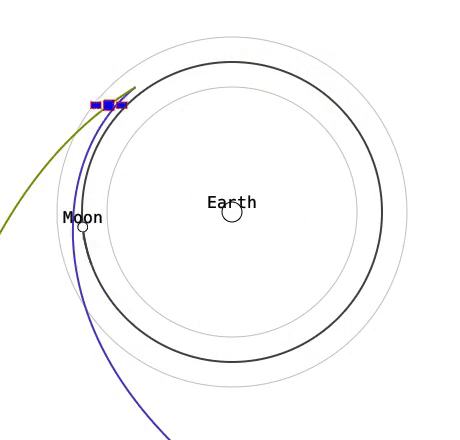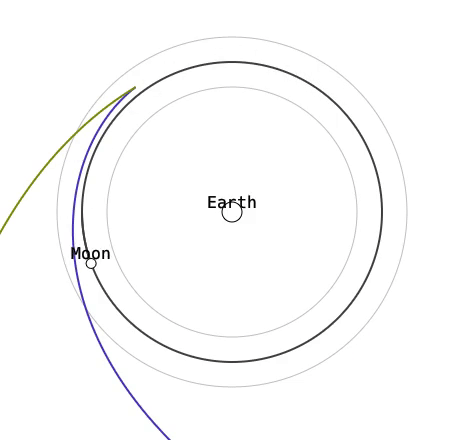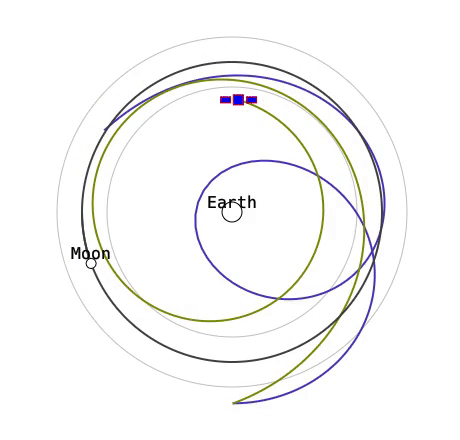
どうやら自動微分でも安定した軌道を発見するのは難しいようです。これにはいくつか理由が考えられます。一つにはカオス性により初期値への解の感度が高すぎて、ちょっと損失関数の勾配を下ろうとしただけで大きくオーバーシュートしてしまうということがあります。そもそも Runge-Kutta 法のステップが大きいためシミュレーション自体が誤差を持ち、特に重力原に近い時に不正確な予測になってしまうということもあります。しかし、あまり時間のステップを小さくすると全体の式が大きくなりメモリ使用量と計算時間に影響します。ここら辺はメモリ使用量を抑える手法がこちらのチュートリアルの最後に触れられており、改善の余地はありそうです。

また、この問題では人口衛星の初期速度のみがコントロールできるとしているのでかなり厳しい制約です。実際にはアクティブに軌道を維持するモデル予測制御のような方法が適しているでしょう。

[2023/10/28 追記] 力学車両モデル

Kinematic Bicycle Model というのは、車両の挙動をモデル化する時よく用いられる数学的モデルです。 Google ではトップにヒットするこの記事が参考になります。

Bicycle という名の通り、自転車のように2輪のモデルで、前輪がステアリングを制御します。回転中心が重心でないのと、前後に動かずにその場で旋回することができないので、滑らかでない経路を正確に辿ることは一般的にはできません。このようなモデルは non-holonomic と呼ばれます。このモデルのシミュレーションについては、上記リンク先で解法が説明されているのでここでは繰り返しません。

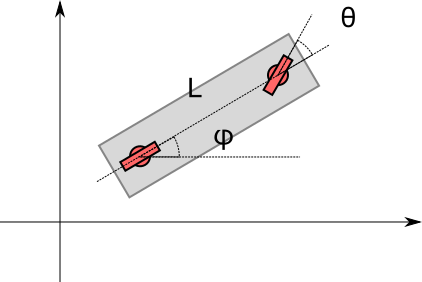
実際の車両は4輪が多いですから、2輪車はあくまでも近似に過ぎませんが、実際の4輪のモデルは必要以上に複雑なのであまり使われません(差動ギアの挙動など正確にモデル化しないとスリップしてしまいます)。

このようなモデルでは、与えられた経路を正確に辿ることはできなくても、できるだけ近い経路を辿るという目的を損失関数に定式化すればモデル予測制御と自動微分でそれなりの解を得ることができます。

脚注

1. これが厳密なモデル予測制御の定義に合致するかどうかはよくわかりません。モデル予測制御のパッケージは通常制約付き最適化ができるソルバーを備えていますが、我々が持っているのは単純な再急降下法と入力信号のボックス制約であり、機能的にはかなり単純なものです。しかし、モデルを立て、それに基づいて予測し、制御を行うという意味ではモデル予測制御と言えると思います。