なぜAAテストにおけるp値は一様分布になるのか？

WEB業界では，ABテストの前にAAテストを行うことがよくあります．これはABテストのランダム化する部分やログを取得する部分，検定時の因果効果の分散の計算方法などが正しいかどうかを確認するためです．

もしABテストの結果が妥当であるための条件が全て満たされている場合は，AAテストにおけるp値(p-value)は一様に分布します．つまり，AAテストを何度も繰り返し行い，その都度，観測されるp値をプロットすると一様分布になるはずです．

もしp値が一様に分布していないと，何かがおかしいということです．そのときは原因の究明が必要になりますが，どこがおかしいかまでは教えてくれないので試行錯誤しなければいけません．

今回は，AAテストでのp値が一様に分布することを説明（かなり大雑把です）し，シミュレーションを通じて，それを確かめます．また単純な分散計算が不適切な場合にp値が一様分布にならないケースもシミュレーションで見ていきます．

p値が一様に分布する理由

話を具体的にするために，あるショッピングサイトのトップページの商品の推薦アルゴリズムのABテストを行う状況を考えます．推薦した商品のインプレッションに対してクリックして商品ページに飛んだかどうかのログをとっているとします．指標としては，全体のクリック率，つまり，(総クリック数) / (総インプレッション数)を考えます．

グループAのインプレッション$i$に対して，$X_i$をクリックしたかどうかの確率変数とします．またグループBのインプレッション$i$に対して，$Y_i$をクリックしたかどうかの確率変数とします．またグループA, Bのインプレッション数を$n, m$とします．$X_i$が従う分布の期待値を$\mu_A$，分散を$\sigma^2_A$，$Y_i$が従う分布の期待値を$\mu_B$，分散を$\sigma^2_B$とします．

ここで注意しなければいけないのは，各インプレッションは独立ではないということです．これは同じユーザーが複数のインプレッションを生み出すことがあるからです．同じユーザーからの複数のインプレッションは，その後クリックにつながりやすさは相関があるはずです．

以下の仮説を立ててt検定を行うことを考えます．

$$H_0: \mu_A = \mu_B \\ H_1: \mu_A > \mu_B$$

ここで，各グループの平均は以下のように計算できます．

$$\bar{X} = \frac1n \sum_{i=1}^n X_i \\ \bar{Y} = \frac1n \sum_{i=1}^n Y_i.$$

$\bar{X}$も$\bar{Y}$も中心極限定理(Central Limit Theorem)により，それぞれ平均$\mu_A$，$\mu_B$の正規分布に従います．独立でない確率変数ですが，同じユーザーの複数のインプレッションを足し合わせて1つの確率変数にしてあげれば独立した確率変数の列と見なせます．

その差は$\bar{X} - \bar{Y}$となります．正規分布同士の差は正規分布に従うので，$\bar{X} - \bar{Y}$も平均$\mu_A - \mu_B$の正規分布に従います．またこの正規分布の分散を$\sigma^2_{\bar{X} - \bar{Y}}$とします．

AAテストにおいて，$X_i$も$Y_i$も同じ分布に従うはずなので$\mu_A = \mu_B$が成り立ちます．このとき，$n$と$m$が十分大きいときは，近似的に

$$\frac{\bar{X} - \bar{Y}}{\widehat{\sigma}_{\bar{X} - \bar{Y}}} \sim \mathcal{N}(0, 1)$$

となります．ここで$\widehat{\sigma}_{\bar{X} - \bar{Y}}$は適当な分散$\sigma_{\bar{X} - \bar{Y}}$の推定量です．(もちろんこの分散の計算方法が大事なのですが一旦置いておきます）

この検定統計量を$T(x_1, \dots, x_n, y_1, \dots, y_m)$とおいて，実際の観測データを$\{x_i\}_{i=1}^n$，$\{y_i\}_{i=1}^m$だとすれば，p値は観測されたデータより極端な例が起こる確率で，以下のように書けます．

$$\Pr\Big(T(X_1, \dots, X_n, Y_1 \dots, Y_m) > T(x_1, \dots, x_n, y_1, \dots, y_m)|\mu_A = \mu_B \Big),$$

$X_i$も$Y_i$も同じ期待値を持つ条件のもと（＝帰無仮説が正しいもと）での条件付き確率となります．

ということで，p値の確率の中身の不等式は，観測データも確率変数と見なせば，どちらも標準正規分布(standard normal distribution)に従うので，p値は独立した２つの標準正規分布$Z_1, Z_2$を用いて，$\Pr(Z_1 > Z_2)$と書けます．すると，

$$\Pr(Z_1 > Z_2) = 1 - \Phi_{Z_1}(Z_2).$$

ただし，$\Phi$は標準正規分布$Z_1$の累積密度関数(Cumulative distribution function)です．

ある累積密度関数$F$に従う確率変数$W$を$F$で変換した確率変数$F(W)$は$[0,1]$の一様分布に従うので，$\Phi_{Z_1}(Z_2)$は$[0,1]$の一様分布に従います．よって$1 - \Phi_{Z_1}(Z_2)$も$[0,1]$の一様分布に従います．

したがって，AAテストにおいてp値は一様に分布します．

シミュレーション

この章ではシミュレーションで仮定が正しい場合にp値が一様に分布し，分散の計算が間違っている場合はp値は一様分布に従わないことを確認します．まず上の例での状況を再現するために以下のようにデータを生成します．

• 各ユーザー$u$のインプレッション数$n_u$は対数一様分布に従って生成(整数化し絶対値を取る)
• 各ユーザー$u$のクリック率$p_u$をベータ分布から生成
• 各ユーザーのクリック数を二項分布$\text{Bin}(n_u, p_u)$から生成

ベータ分布のパラメタは全体のクリック率から算出します．

# required packages
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt

# setting
view_sigma = 1.0
global_click_rate = 0.2
beta = 50.0 # Parameter for beta dist.
n = 300 # The number of users in group A 
m = 200 # The number of users in group B

def generate_click_data(n, m, view_sigma, global_click_rate, beta):
    alpha = global_click_rate * beta / (1 - global_click_rate) # Parameter for beta dist.

    # generate impression data
    imps_a = np.abs(np.random.lognormal(mean=1.0, sigma=view_sigma, size=n).astype(int))
    imps_b = np.abs(np.random.lognormal(mean=1.0, sigma=view_sigma, size=m).astype(int))

    # generate click data
    user_click_rates_a = stats.beta(alpha, beta).rvs(n)
    user_click_rates_b = stats.beta(alpha, beta).rvs(m)
    clicks_a = stats.binom(n=imps_a, p=user_click_rates_a).rvs()
    clicks_b = stats.binom(n=imps_b, p=user_click_rates_b).rvs()
    
    return (imps_a, clicks_a, imps_b, clicks_b)

これで同じ分布から生成されたクリックログ2つを生成する関数が定義できました．この関数を用いて，AAテストを行います．

まずはt統計量を算出する際の分散の計算方法を間違えたとします．i.i.d.のサンプルが得られた場合に2標本のt検定でよく使われる分散の計算方法を用いてしまった場合，各インプレッションは独立ではないので分散の推定がうまくいきません．そのため，最終的な正規分布の分散は1ではなくなります．よってp値は一様分布にはならないことが期待されます．それを確かめます．

def cal_wrong_se(ctr_a, clicks_a, ctr_b, clicks_b):
    n_a = clicks_a.shape[0]
    n_b = clicks_b.shape[0]
    s2_a = ((clicks_a - ctr_a) ** 2).sum()
    s2_b = ((clicks_b - ctr_b) ** 2).sum()
    s2 = ((n_a - 1) * s2_a + (n_b - 1) * s2_b) / (n_a + n_b - 2)
    return np.sqrt(s2 * (1/n_a + 1/n_b))
        
n_aa_tests = 1000
p_vals = []
for _ in range(n_aa_tests):
    imps_a, clicks_a, imps_b, clicks_b = generate_click_data(n, m, view_sigma, global_click_rate, beta)
    ctr_a = clicks_a.sum() / imps_a.sum()
    ctr_b = clicks_b.sum() / imps_b.sum()
    se_ab = cal_wrong_se(ctr_a, clicks_a, ctr_b, clicks_b)
    t_stat = (ctr_a - ctr_b) / se_ab
    p_val = 1 - stats.norm.cdf(t_stat)
    p_vals.append(p_val)
    
# plot p value distribution
fig, ax = plt.subplots()
ax.hist(p_vals, bins=np.arange(0, 1, 0.1))
ax.set_title("distribution for p-values. Wrong Variance Estimation")
ax.set_xlabel("p-value")
ax.set_ylabel("counts")

p値が0.5あたりに分布しているので，分散を過大評価してしまっていることがわかります．

次にブートストラップ法を用いて正しく分散を推定した場合を見てみます．

def cal_se_with_bootstrap(imps_a, clicks_a, imps_b, clicks_b, B=1000):
    diffs = []
    n = imps_a.shape[0]
    m = imps_b.shape[0]
    for _ in range(B):
        chosen_idx_a = np.random.choice(np.arange(n), size=n, replace=True)
        chosen_idx_b = np.random.choice(np.arange(m), size=m, replace=True)
        ctr_a = clicks_a[chosen_idx_a].sum() / imps_a[chosen_idx_a].sum()
        ctr_b = clicks_b[chosen_idx_b].sum() / imps_b[chosen_idx_b].sum()
        diff = ctr_a - ctr_b
        diffs.append(diff)
    return np.std(diffs)

n_aa_tests = 1000
p_vals = []
for _ in range(n_aa_tests):
    imps_a, clicks_a, imps_b, clicks_b = generate_click_data(n, m, view_sigma, global_click_rate, beta)
    ctr_a = clicks_a.sum() / imps_a.sum()
    ctr_b = clicks_b.sum() / imps_b.sum()
    se_ab = cal_se_with_bootstrap(imps_a, clicks_a, imps_b, clicks_b)
    t_stat = (ctr_a - ctr_b) / se_ab
    p_val = 1 - stats.norm.cdf(t_stat)
    p_vals.append(p_val)

# plot p value distribution
fig, ax = plt.subplots()
ax.hist(p_vals, bins=np.arange(0, 1, 0.1))
ax.set_title("distribution for p-values. Boostrap Variance Estimation")
ax.set_xlabel("p-value")
ax.set_ylabel("counts")

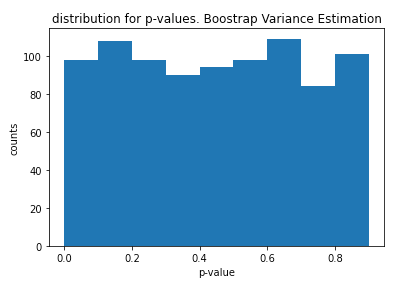
p値が一様に分布していることがわかります．

このように独立の仮定が必要な計算式を用いてしまった場合などのチェックにも使えます．他にも例えば，片方のグループのスマートフォンのログだけ欠損してしまった場合など基盤のバグなどにも応用ができます．もちろんAAテストを行ってp値が一様に分布したからといって，100%信頼できる結果が得られるとは限りませんが，Sanity checkとしては機能すると思います．

間違いなどを見つけた場合，ぜひ教えていただけると幸いです．

リファレンス

[1] Kohavi, Ron, et al. "Trustworthy online controlled experiments: Five puzzling outcomes explained." Proceedings of the 18th ACM SIGKDD international conference on Knowledge discovery and data mining. 2012.

[2] Kohavi, Ron, Diane Tang, and Ya Xu. Trustworthy online controlled experiments: A practical guide to a/b testing. Cambridge University Press, 2020.