より良い意思決定がしたいので、under-powered なテストを避けるためのABテスト設計方法を調べた
n週連続推薦システム系論文読んだシリーズ 37 週目の記事になります:)
ちなみに36週目は 言語モデルと知識グラフを良い感じにalignして、knowledge-awareなニュース埋め込み表現を作る推薦手法DKNの論文を読んだ でした!
(一応、推薦システムもオンライン実験するので許してください!:pray:)
はじめに:
- 本資料は、以下の参考資料を元にunder-powered なテストを避ける為のABテストの設計方法について調べ、自分なりの解釈・理解をまとめたものです:)
- 下記の参考文献たちと出会ったきっかけ :pray: Work In ProgressさんのPodcast配信 #145 Netflixから学ぶA/Bテストで間違った意思決定をしないためのプラクティス
- NetflixさんのABテストに関するブログ連載
- X(旧Twitter)さんのABテストのサンプルサイズに関するブログ
- web上でのコントロール実験に関するpracticeをまとめた論文
- 下記の参考文献たちと出会ったきっかけ :pray: Work In ProgressさんのPodcast配信 #145 Netflixから学ぶA/Bテストで間違った意思決定をしないためのプラクティス
- 上記の文献ではABテストを経てより良い意思決定のための工夫として様々紹介されています。
- 本資料は、より良い意思決定のために意識すべきことの1つとして、under-powered なテストを避ける為の設計方法に焦点を当て、推薦システムを題材とした架空のABテストを想定しながら手順を整理します。
- もし理解の誤りや気になる点などあれば、カジュアルに絵文字をつけてコメントしていただけると喜びます...!:thinking:
under-poweredなテストとは??
ABテストにおける二種類の不確実性
- ABテストで得られる観測結果は、確率変数(=確率的に変動する値)なので、結果には不確実性がある。
- (ex. 公平なコインを100回投げた時の表の出る回数は、必ずしも100回中50回とは限らないよね...!)
- ABテストによる意思決定には、大きく2種類の不確実性がある:
- Type I error: false positive
- 本当は施策に効果がないのに、効果があると判定しちゃう。
- Type II error: false negative
- 本当は施策に効果があるのに、効果がないと判定しちゃう。
- Type I error: false positive
- under-poweredなテストは、Type II errorのリスクが高くなっちゃってるテストのこと。
under-poweredなテストとは??
- under-poweredなテスト = 検出したい真の効果の大きさに対して、検出力(power, 指定した大きさの効果を正しく検出できる確率)が小さくなってしまっているテスト。
- under-poweredなテストだと... 本当は施策に効果があるのに効果がないと判定されてしまうリスク(i.e. false negativeの確率)が高くなってしまう。
- -> under-poweredなテストを避ける為に、いい感じにABテストを設計する必要があるよね...!
- (なんとなく、ABテストでより良い意思決定をするための前提条件というか、必要条件なのかなという認識になりました...!たぶん十分条件ではない:thinking:)
(自分の理解)under-poweredなテストを避けるためになにを設計できる?
- under-poweredなテストを避けるために、我々がABテスト開始前に設計できるのは、ざっくり以下の要素っぽい:
- significance level(有意水準):
- 慣例では5%が採用される事が多い。domainによっては異なるのかも。
- (Netflixさんのブログではacceptable false positive rateとも表現されてて、個人的にはこっちの方が直感的で意味がわかりやすくて好きぇ~:thinking:)
-
postulated effect size(仮定された効果量):
- 仮定された施策の効果の大きさ。検出力の値はABテストを経て検出したい効果量に依存するので、事前に設定しておく必要がある。
- (これを指定しなくてもp値は算出できて、有意か否かの判定ができてしまうから罠だ...!:thinking:)
-
sample size(サンプルサイズ):
- ABテストで収集すべき実験単位のサンプル数(実験単位がユーザの場合はユーザ数)。
- ざっくりサンプルサイズを増やしたら、小さい差を検出しやすくなって、検出力は上がる。
-
metricの変動性:
- metricの変動性(分散)によって、他の全ての条件が同じでも検出力が異なる。metricの変動性が大きく不安定であるほど、実験の不確実性が高くなる。
- 評価に使用するmetricの選び方だったり、metricの変動性を抑える工夫が可能。
- significance level(有意水準):
推薦システムの架空のABテストを例に、under-poweredなテストを避けつつ設計してみるぞ!
(ここで強引に推薦システムにからめてみました...!:pray:)
架空のABテストシナリオ
- 架空のABテストシナリオ:
- ECサイトのメイン画面の「おすすめセクション」内では、人気商品を表示している。**現在のconversion rateは5%(0.05)**である。(controll)
- 各ユーザの既存の嗜好と合致した商品を表示できれば、ユーザが好きな商品に出会える機会が増えユーザ体験が向上するのではという仮説を立て、機械学習モデルによるパーソナライズ施策を実装した(treatment)。
- 施策の有効性を判断(意思決定)するために、ABテストを実施することにした。
- ABテストの設定:
-
OECとしてconversion rateを採用する。(今回はbinary metricsを採用してみた! non-binary metricsを採用するケースも後半で試してみる:thinking:)
- ちなみに**OEC(Overall Evaluation Criterion)**とは? 実験を経て改善させたい目的となる定量的な指標 (i.e. netflixさんの資料における primary decision metric?:thinking:)
- 施策によってOECを+5%改善することを期待する。
- variantは2つ(controlとtreatment)。各variantには同じサンプルサイズを割り当てる。
- 有意水準(i.e. acceptable false positive rate)=5%。(今回は特に慣例から外れる理由はなさそうなので:thinking:)
-
OECとしてconversion rateを採用する。(今回はbinary metricsを採用してみた! non-binary metricsを採用するケースも後半で試してみる:thinking:)
基本的には、有意水準、評価するmetric、仮定された効果量を決めた上で、under-poweredなテストにならないような良さげなサンプルサイズの導出を試みます...!
(ちなみに) 評価するmetric: binary metricかnon-binary metricか
今回はABテストの統計的仮説検定で評価するmetricとして、binary metricsであるconversion rateを採用してみた。(後半で少しnon-binary metrics ver.もやってみる)
- binary metrics:
- 例えば、conversion rateは、ユーザが閲覧した商品を購入するか、しないかのbinary metricと言える。
- 他の例: CTR、プッシュ通知の開封率、解約率、etc...。
- binary metricsの場合、ABテストの設計時にmetricの変動性(分散)を指定する必要はない。(期待値から分散が導出できるので...!)
- non-binary metrics:
- 例えば、ユーザ一人当たりのconversion金額は、non-binary metricと言える。
- 他の例: ユーザの滞在時間、サーバーのlatency、開封数、解約数、etc...。
- non-binary metricsの場合、ABテストの設計時にmetricの変動性(分散)も指定する必要がある。(どうやら分散を標本データから仮定する方法が、t検定的なアプローチっぽい?:thinking:)
サンプルサイズの導出作戦
さて、under-poweredなテストにならないような理想的なサンプルサイズの導出を試みます。作戦の手順は以下です:
-
- null distribution(帰無分布)を描画する。
- 帰無仮説(=施策に効果がないという仮説)が正しい場合に得られる観測値の確率分布(=null distribution)を描画する。i.e. 確率分布関数を描画する。
-
- rejection region(棄却域)を描画する。
- 設定した有意水準(i.e. acceptable false positive rate)に基づき、null distribution上にrejectin region(棄却域)を描画する。
-
- alternative distribution(対立分布)を描画する。
- 仮定した効果量に基づき、対立仮説が正しい場合に得られる観測値の確率分布(=alternative distribution)を描画する。
-
- 検出力を計算する。
- null distribution, rejection region, alternative distributionが決まれば、検出力が決まる。
-
- 検出力が0.8になるようなサンプルサイズ
n
- 検出力が0.8になるようなサンプルサイズ
(ちなみに、今回はt検定やz検定のような特定の統計的仮説検定のフレームワークは特に意識せず、null distributionとalternative distributionを導出することで、検出力や良さげなサンプルサイズなどを計算してみます...!)
手順1: null distribution(帰無分布)を描画する。
- 帰無仮説: control群とtreatment群で、真のconversion rateには差がない。
(i.e. control群の真のconversion rate = treatment群の真のconversion rate = 5%) - → controll群のconversionも、treatment群のconversionも、期待値5%(p=0.05)のベルヌーイ分布に従うbinaryの確率変数である。
- → サンプル数
n \bar{x}_{cont}, \bar{x}_{treat} p p(1-p)/n - null distributionを、両者の標本平均の差 (確率変数
X = \bar{x}_{treat} - \bar{x}_{cont} - → 期待値
p_{treat} - p_{cont} = 0 p(1-p)/n + p(1-p)/n = 2p(1-p)/n - → null distributionは、期待値0、分散
2 * 0.05 (1-0.05)/n
- → 期待値
- 数式にすると以下のような感じ:
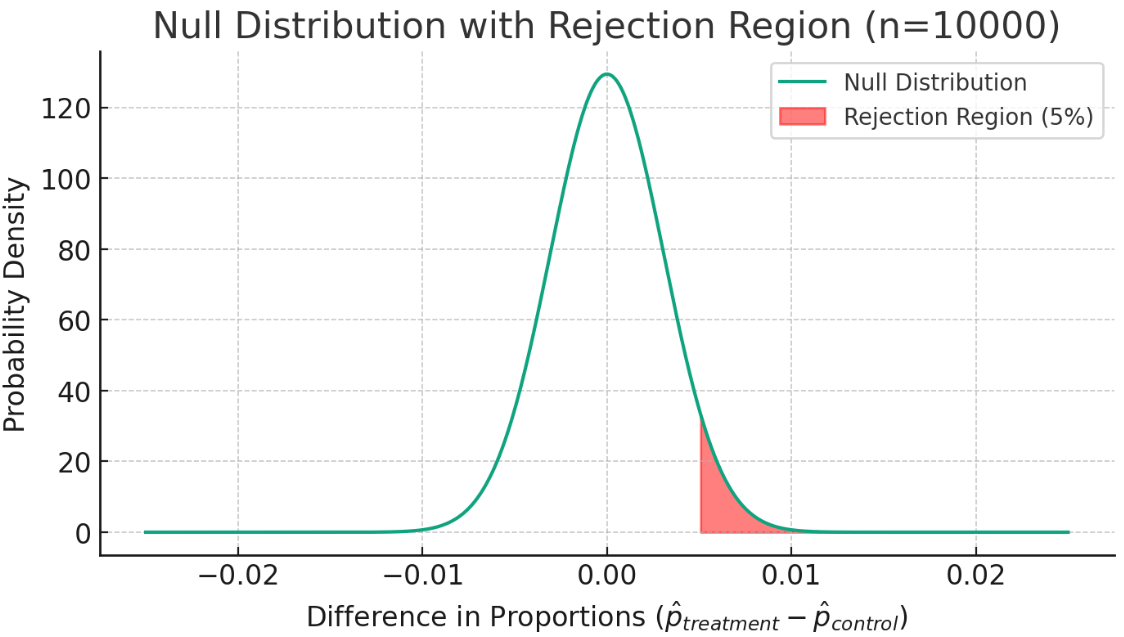
以下の図は、n=10000の場合のnull distributionを描画したもの。

手順2: rejection region(棄却域)を描画する。
有意水準(accetable false positive rate) = 5% の条件をもとに、null distributionにおいて、rejection region(棄却域)を算出する。
-
rejection region(棄却域) = null distributionにおいて確率質量の累積値が有意水準を超えないような、最も発生しづらい観測結果の値域。観測結果がこの値域に含まれることと、p値が有意水準よりも小さくなることは同義。
- -> 今回の場合は片側検定を想定するので、null distributionの95%値よりも右側にrejection regionが描画される感じ...!:thinking:
- -> 具体的には、null distributionの累積質量関数を
cmf(\cdot) cmf(x) < 1.0 - 0.05 x - (ちなみに、rejection regionの境界値をcritical valueと呼ぶ。今回の場合は
cmf(x) = 1.0 - 0.05 x
以下の図は、n=100の場合のnull distributionにおけるrejection regionを描画したもの。(
手順3: alternative distribution(対立分布)を描画する。
- 対立仮説: control群の真のconversion rate = 5%、treatment群の真のconversion rate = 5%×(1 + 0.05) = 5.25% (OEC+5%の改善を目指すので...!)
- -> controll群のconversionは期待値
p_{cont} = 0.05 p_{treat} = 0.0525 - -> サンプル数
n - control群:
P(\bar{x}_{cont}|p_{cont}=0.05) = Norm(0.05, 0.05(1-0.05)/n) - treatment群:
P(\bar{x}_{treat}|p_{treat}=0.0525) = Norm(0.0525, 0.0525(1-0.0525)/n)
- control群:
- null distributionと同様に、alternative distributionを両者の標本平均の差(確率変数
X = \bar{x}_{treat} - \bar{x}_{cont}
以下の図は、n=10000の場合のalternative distributionを描画したもの。

手順4: 検出力を計算する。
-
検出力 = alternative distributionのうち、rejection regionに含まれる確率質量の割合。(i.e. 対立仮説が正しい場合に帰無仮説を正しく棄却できる確率 = 期待した効果量で条件づけた場合のtrue positiveの確率...!)
- 今回の場合は数式で表すときっとこんな感じ...!
- 視覚的には...
- 検出力の大きさ = (alternative distributionの中の青エリアの面積) / (alternative distribution全体の面積)
- (縦軸の値は確率密度なので、面積は質量になるので...!:thinking:)
- 検出力の大きさ = (alternative distributionの中の青エリアの面積) / (alternative distribution全体の面積)

- (なるほど...!alternative distributionを仮定しないと、すなわち検出したいeffect sizeを仮定しないと、検出力は計算できないのか...!:thinking: p値やrejection regionは仮定しなくても計算できるけど...! 逆にp値の計算には観測結果が必要だけど、検出力の計算には不要:thinking:)
ちなみにサンプルサイズ
手順5: 検出力が0.8になるようなサンプルサイズ n
手順1~4を踏まえると、検出力は、null distributionとalternative distributionの形、およびrejection regionによって一意に定まる。
- 2つの確率分布のパラメータは、metricで仮定する効果量 (
p_{treatment}-p_{controll} n - → 検出力は、有意水準、metricで仮定する効果量、サンプルサイズの関数で表せそう。(non-binary metricの場合は、metricの変動性(分散)も関数に含まれるはず...!:thinking:)
どうしたら検出力が上がりそうか考えてみる。
alternative distributionのより多くのエリアがrejection regionに含まれるようにするには...??
-
- 有意水準を高くする(i.e. acceptable false positive rateを高くする)
- → null distributionのrejection regionが広くなる。
-
- 仮定する効果量を大きくする
- → alternative distributionの峰が右側に移動する。
- 仮定する(i.e. 検出したい)効果量をより大きく設定するには、効果的な施策を作る必要があるよね...!:thinking:
-
- サンプルサイズを大きくする
- → null distributionとalternative distributionの分散が小さくなる。
-
- metricの変動性(分散)を小さくする
- → null distributionとalternative distributionの分散が小さくなる。
とりあえず指定した条件における検出力を算出できるようになったので、あとは全探索的なアプローチで、良さげなサンプルサイズ
(ちなみに) サンプルサイズの公式
ちなみにpractice論文及びXさんのブログでは、有意水準5%、検出力80%における最小サンプルサイズの公式として、以下が紹介されてた。(powerの式から式変形を色々頑張ったらたどり着きそう...??:thinking:)
ここで、
-
n -
\sigma - (たぶんnull distributionとalternative distributionで同じ標準偏差を仮定してる感じ...!)
-
\Delta
(ちなみに) minimal detectable effectの考え方
- Xさんのブログ内では、Minimal Detectable Effectの概念が紹介されていた。
- 検出力は、有意水準、metricで仮定する効果量、サンプルサイズ、metricの変動性の関数で表せる。
- → 式変形したら、検出力80%で検出できる最小の効果量を求めることができる。
- → この最小の効果量を、検出力80%のMinimal Detectable Effect(検出可能な最小効果)、すなわち0.8MDEと呼ぶ。
- 0.8MDEの値が検出したい効果量よりも小さくなるように他の条件を調整しよう、みたいな考え方...!(まあ結局やることは同じなんだけど)
OECの選択と必要なサンプルサイズについて
OECの変動性がサンプルサイズに与える影響
- practice論文では、OECとしてconversion rateと収益(revenue)をそれぞれ採用した例を紹介していました。
- 以下のシナリオ:
- ECサイトにて、既存ではだいたいユーザのうちの5%が購入にいたる。
- 購入するユーザは平均75ドルほど使うので、一人当たり収益は平均3.75ドル(ユーザのうち95%は0ドルなので)
- 一人当たり収益の標準偏差は30ドルとする。
- (一人当たり収益が従う分布は、正規分布ではないよね。でも結局、標本平均は正規分布に従うと近似できるから、期待値と標準偏差がわかってれば、null distributionやalternative distributionを仮定できてOKか...!:thinking:)
- 有意水準5%のABテストで、OECの5%の改善を検出したいとする。必要なサンプルサイズは...
- OEC=conversion rate (binary metric)の場合:
n = 16 \times \frac{0.05 \times (1-0.05)}{0.05 \times 0.05}^2 \approx 122,000人
- OEC=収益 (non-binary metric) の場合:
n = 16 \times \frac{30^2}{(3.75 \times 0.05)}^2 \approx 409000人
- OEC=conversion rate (binary metric)の場合:
- →収益ではなくconversion rateをOECとして使用することで、実験に必要なサンプルサイズを1/3に減らせる。つまり、OEC=収益では6週間かかる実験が、OEC=conversion rateでは2週間に短縮できる。(or 実験に割り当てるユーザ割合を減らせる...!)
- 従って、変動性の低いOECを検討することは検討の余地がある...!。
- OECは事前に決定すべきことに注意...!
- false positiveのリスクが高くなるので...!(familywise type I error)
- (複数のOECで何回も統計的仮説検定しちゃうと、多重検定になるから??:thinking:)
Trigger analysisとサンプルサイズの話
- Trigger Analysis = 施策の影響を受けないユーザのフィルタリングし、施策の影響を受けた(i.e. Triggerされた)ユーザだけを分析対象とすること。
ex.) チェックアウト(ECサイトにおける決済)プロセスに変更を加えて、conversion rateをOECとする場合:
- (感覚的にも、全ユーザをvariantに割り当てたとしても、実際にはチェックアウトプロセスを開始したユーザのみを分析する必要がありそうだよね:thinking:)
- 10%のユーザがチェックアウトを開始し、そのうちの50%のユーザがチェックアウトを完了すると仮定する。
- OEC=conversin rateとして、OEC+5%の改善を検出したいとする。必要なサンプルサイズは...
- 全ユーザで分析する場合:
- 前述の例と条件が同じなので、サンプルサイズは122,000人必要。
- Triggerされたユーザのみで分析する場合:
- OECの平均が0.5, 標準偏差が0.5×(1-0.5)になる。
- ->
16 \times \frac{0.5 \times (1-0.5)}{0.5 \times 0.05}^2 \approx 6400 - チェックアウトを開始しないユーザが90%なので、全体で必要なサンプルサイズは6400/0.1=64000人。(サンプルサイズを1/2に減らせた...!)
- 全ユーザで分析する場合:
- → Trigger AnalysisによってOECの標準偏差を小さくできると、検出力80%を得るために必要なサンプルサイズを減らせる。
- (特にbinary metricの場合、trigger analysisによって逆にOECの変動性があがっちゃうケースもあるのかも...? 例えばフィルタリングする前はp=0.5で、フィルタリングしたらp=0.8である場合とか...!:thinking:)
- (OECの選択と同様に、Trigger Analysisするか否かも基本的に事前に決めたほうがよさそう...!というか、OECの選択の一部といえるかも:thinking:)
適切なサンプルサイズを認識 & 最小限のサンプルサイズで実験する価値:
サンプルサイズめっちゃ増やしたらいいのでは??って話
-
サンプルサイズを増やしたら検出力あがるんなら、サンプルサイズを増やせるだけ増やしたらいいのでは??
- -> サンプルサイズを無限にできれば、どんなに微小な効果量でも、どんなに変動性が大きいOECを採用しても、under-poweredなテストを回避して高いtrue posive確率で有意だと判断できるじゃん...!
-
「どんなに微小な効果量でも、高い確率で検出できる」ことは、統計的に有意な結果を得ることができるという意味では確かに正しい。
- ただし統計的に有意な結果を得ることができたからといって、それが実務における意思決定の観点で有用な結果であるとは限らない。
(- サンプルサイズをめっちゃ増やしたら、統計的に有意だと判断された際にその効果量が無意味なほど微小である可能性がどんどん高くなる...!:thinking:)
- ただし統計的に有意な結果を得ることができたからといって、それが実務における意思決定の観点で有用な結果であるとは限らない。
-
netflixさんブログでは、reasonable(合理的)でmeaningful(意味のある)な効果量を検出するために、適切なサンプルサイズを認識することが重要だと紹介されてた。
- ex.) ある施策によってOECが0.001%改善することを検出できたとしても、それは合理的かつ意味のある改善なのか...? (サンプルサイズをめっちゃ増やしたら0.001%の差でも有意って判定される可能性が高くなるし...!:thinking:)
-
reasonableについて:
- プロダクト改善やビジネスにおいてOECがどれだけ改善される事が合理的かは判断が難しい。ドメイン知識や過去の実績を踏まえて判断する必要がある。
- あるOECの0.001%の改善が、プロダクト全体のKPIの改善に想定外に大きく寄与する可能性も0ではない。
- プロダクト改善やビジネスにおいてOECがどれだけ改善される事が合理的かは判断が難しい。ドメイン知識や過去の実績を踏まえて判断する必要がある。
-
meaningfulについて:
- 何がmeaningfulかは、実験の影響範囲(ユーザ体験, latency, バックエンドシステムの技術的なパフォーマンス, etc.)や、treatmentの労力やコストによって異なる。
- ex.OECの0.1%の改善によるビジネス上の利益よりも施策を導入&運用するコストが大きい場合、OECの0.01%の変化を高い確率で検出できるようなABテストを設計&実施する意味はない。
- → そのようなサイズの効果を正しく検出できても、意思決定に意味のある(meaningfulな)変化ではないから...!
-
(思ったことメモ)
- 統計的仮説検定って結局binaryの結果 (=有意な差があると言えるか言えないか) しか出力しないから、仮に合理的で意味のある効果量に対して検出力0.8という設定で実験して、有意な結果が得られたとしても、本当は検出力0.1くらいの微小な効果量での1/10のtrue positiveを引いた可能性もあるんだよな~:thinking:
- 検出力(true positiveの確率) 0.8 って効果量で条件づけた確率だから、有意だった時に、単純に「80%の確率でこの施策の効果量はxxxです!」って判断できる訳では無いよな...! :thinking:
- だから「under-poweredな実験を避けるように設計する」ことは、良い意思決定をするための必要条件の1つだけど十分条件ではなくて、それ以外にも色々な要素を踏まえた上で意思決定をする必要がありそう...!:thinking:(secondary metricsも見よう! みたいな話とか...!参考資料に色々書いてあった!)
適切なサンプルサイズを認識 & 最小限のサンプルサイズで実験する価値:
-
- 施策のリスクの影響範囲を最小限に抑えられる:
- 施策(ex. 新機能)にはリスクが伴う。ユーザ体験の思わぬ悪化とか。
- より良い意思決定ができる可能性が高い & リスクを抑えた最小限のサンプルサイズでテストを実施できたら嬉しい...!
-
- ユーザが同時に複数の実験に割り当てられる機会を減らせる:
- 複数の実験間の相互作用みたいなことを考慮して、効果を推論するのは難しいらしい。
- その相互作用の発生を抑える観点から、施策の影響を測定するのに1%のトラフィックで十分であれば、1%のみを使用する方が望ましい。
-
- 1日あたりのTrafficからABテスト実施期間を決定できる:
- 逆に、適切なサンプルサイズを認識できていない場合、いつまでABテストを実施すればいいのかわからない...!
- 仮にABテストの観測データを使って統計的検定を行い、有意だと判断されなかった場合、その理由が「施策の効果が期待よりも小さかったから」なのか、「サンプルサイズが足りなかったから」なのかを区別する事ができない!
- → その結果、以下の悪影響がありそう。
- ABテスト期間を延長しながら何度か検定を繰り返してしまい、false positiveのリスクが高くなる
- サンプルサイズを過剰に増やしてしまい、not reasonable or not meaningfulな差に対して有意だと判定してしまうリスクが高くなる。
- 次の施策や開発に取り掛かるタイミングが遅れ、開発リソースの無駄遣いにつながる...!
終わりに
- より良い意思決定がしたいと思って、netflixさんやtwitterさんのテックブログや、practiceをまとめた論文を読んだよ!
- より良い意思決定をするために意識すべきことの内の1つ「under-poweredなABテストを避けること」のために、事前に設計できる要素を整理し理解をまとめたよ!
- 推薦システムのABテストを例に、最小サンプルサイズnの導出手順をまとめたよ!
- null distribution → rejection region → alternative distribution → power → n の手順で導出できそうだよ!
- OECの選択とサンプルサイズの関連:
- 必要なサンプルサイズを小さくすることができるので、OECの変動性を小さくする工夫には検討する価値があるよ!
- 適切なサンプルサイズを認識 & 最小限のサンプルサイズで実験する価値:
- サンプルサイズをめっちゃ増やせば検出力あがっていいんじゃないの??
- -> 意思決定する上で価値の無い差を有意と判定してしまうリスクがめっちゃ上がっちゃうよ!
- 適切なサンプルサイズを認識し、最小限のサンプルサイズで実験する事には色々価値があるよ!
- 逆に、適切なサンプルサイズを認識できていない場合、色々と不利益を被りそうだよ!
- サンプルサイズをめっちゃ増やせば検出力あがっていいんじゃないの??
- 思った事:
- 統計的仮説検定って結局binaryの結果(=有意な差があると言えるか言えないか)しか返さないから、良い感じにサンプルサイズとか設計できたとしても不確実性は避けられないよ!
- だから「under-poweredな実験を避けるように設計する」ことは、良い意思決定をするための必要条件の1つだけど十分条件ではなくて、それ以外にも色々な要素を踏まえた上で意思決定をする必要がありそうだよ! (secondary metricsも見よう、みたいな話とか...!参考資料に色々書いてあった!)
最後まで読んでいただきありがとうございました!
もし気になった点や自分の理解に誤ってる点などあれば、ぜひカジュアルに絵文字をつけてコメントいただけるとめちゃめちゃ喜びます:)
参考文献:
- 下記の参考文献を見つけたきっかけWork In ProgressさんのPodcast配信
- NetflixさんのABテストに関するブログ連載
- X(旧Twitter)さんのABテストのサンプルサイズに関するブログ
- web上でのコントロール実験に関するpracticeをまとめた論文
(おまけ)検出力が0.8になるようなサンプルサイズ n
最後に、実際にunder-poweredな実験を避ける為の良さげなサンプルサイズを、実際に算出を試みようと思います。
公式の導出過程は追えていないので、特定の条件の検出力を算出する処理を実装した上で、検出力が0.8を超えるようなサンプルサイズを全探索的に算出を試みます...!
検出力を算出する関数を用意
まずは特定の条件での検出力を算出する関数を実装します。
関数signature (i.e. 観察可能な振る舞い?) は以下のような感じにしてみます。
def calculate_statistical_power(
null_distribution: ProbabilityDistribution,
alternative_distribution: ProbabilityDistribution,
acceptable_false_positive_rate: float = 0.05,
alternative_hypothesis_type: AlternativeHypothesisType = AlternativeHypothesisType.GREATER_THAN,
) -> float:
pass
引数としてnull distribution、alternative distribution、有意水準、検定のタイプ(片側検定とか!)を受け取り、検出力を返します。
単体テストは以下のような感じにしてみます。
def test_calculate_statistical_power() -> None:
# Arrange:
## コインが公平じゃなくて、表が64%くらい出やすい不公平コインなんじゃないか、みたいなテストを想定してます(netflixさんのブログの例)
n = 100
null_distribution = ProbabilityDistribution(
mean=0.5,
std=np.sqrt(0.5 * (1 - 0.5) / n),
)
alternative_distribution = ProbabilityDistribution(
mean=0.64,
std=np.sqrt(0.64 * (1 - 0.64) / n),
)
acceptable_false_positive_rate = 0.05
alternative_type = AlternativeHypothesisType.GREATER_THAN
# Act
actual_statistical_power = calculate_statistical_power(
null_distribution,
alternative_distribution,
acceptable_false_positive_rate,
alternative_type,
)
# Assert
expected_statistical_power = 0.886 # この解答は、とりあえずchat gptに聞きました!
assert np.isclose(actual_statistical_power, expected_statistical_power, atol=0.01)
このテストが通ることを目指し、実装の詳細を以下のように書いてみました。
from alternative_hypothesis_type import AlternativeHypothesisType
from normal_distribution import ProbabilityDistribution
from typing import Optional
def calculate_statistical_power(
null_distribution: ProbabilityDistribution,
alternative_distribution: ProbabilityDistribution,
acceptable_false_positive_rate: float = 0.05,
alternative_hypothesis_type: AlternativeHypothesisType = AlternativeHypothesisType.GREATER_THAN,
) -> float:
left_critical_value, right_critical_value = get_rejection_region(
null_distribution, acceptable_false_positive_rate, alternative_hypothesis_type
)
# 対立分布のうちrejection regionに含まれる部分の面積を算出
true_positive_area = 0
if left_critical_value:
true_positive_area += alternative_distribution.cdf(left_critical_value)
if right_critical_value:
true_positive_area += 1 - alternative_distribution.cdf(right_critical_value)
return true_positive_area / 1
def get_rejection_region(
null_distribution: ProbabilityDistribution,
acceptable_false_positive_rate: float,
alternative_type: AlternativeHypothesisType,
) -> tuple[Optional[float], Optional[float]]:
"""critical valueのタプルを返す
- 片側検定の場合は片方のみの値が入る
"""
assert 0 < acceptable_false_positive_rate < 1
has_left_rejection_region = alternative_type.has_left_rejection_region
has_right_rejection_region = alternative_type.has_right_rejection_region
if has_left_rejection_region and has_right_rejection_region:
return (
null_distribution.ppf(acceptable_false_positive_rate / 2),
null_distribution.ppf(1 - acceptable_false_positive_rate / 2),
)
if has_left_rejection_region:
return (null_distribution.ppf(acceptable_false_positive_rate), None)
return (None, null_distribution.ppf(1 - acceptable_false_positive_rate))
テストが通るようになったので次へ行きます!
検出力が0.8になるようなサンプルサイズ n
まず、以下のような単体テストを用意します。
今回は、OECとしてbinary metricを使用することを前提とした DesirableSampleSizeSimulatorWithBinaryMetricクラスを用意しました。(クラスにする必要はなかったかな~と迷いつつ...)
テストケースはpractice論文のsection 3.2の例の値を使ってみました。
def test_desirable_sample_size_calculation_with_binary_metric() -> None:
# Arrange
significance_level = 0.05 # i.e. acceptable false positive rate
desirable_power = 0.8
## practice論文のsectin 3.2の例の値を使う
control_metric_mean = 0.05
treatment_metric_mean = control_metric_mean * (1 + 0.05) # OEC5%の改善を仮定
sut = DesirableSampleSizeSimulatorWithBinaryMetric(
significance_level,
desirable_power,
)
# Act
desirable_sample_size_actual = sut.calculate(
control_metric_mean,
treatment_metric_mean,
)
# Assert
expected = 121599 # 公式より 16 * (0.05 *(1-0.05))/(0.05 * 0.05)^2
assert expected - 1000 <= desirable_sample_size_actual <= expected + 1000
単体テストがpassすることを目指し、以下のような実装を試みました。
import numpy as np
from alternative_hypothesis_type import AlternativeHypothesisType
from normal_distribution import ProbabilityDistribution
from statistical_power_calculation import calculate_statistical_power
class DesirableSampleSizeSimulatorWithBinaryMetric:
def __init__(
self,
significance_level: float = 0.05,
desirable_power: float = 0.8,
alternative_type: AlternativeHypothesisType = AlternativeHypothesisType.GREATER_THAN,
) -> None:
self.significance_level = significance_level
self.desirable_power = desirable_power
self.alternative_type = alternative_type
def calculate(
self,
control_metric_mean: float,
treatment_metric_mean: float,
) -> int:
for sample_size in range(100, 10**10, 100):
null_dist = self._create_null_distribution(control_metric_mean, sample_size)
alternative_dist = self._create_alternative_distribution(
control_metric_mean,
treatment_metric_mean,
sample_size,
)
power = calculate_statistical_power(
null_dist,
alternative_dist,
self.significance_level,
self.alternative_type,
)
if power >= self.desirable_power:
return sample_size
else:
raise ValueError("The desirable sample size is not found. expected effect size is too small.")
def _create_null_distribution(
self,
control_metric_mean: float,
n: int,
) -> ProbabilityDistribution:
null_mean = control_metric_mean - control_metric_mean
null_std = np.sqrt(2 * control_metric_mean * (1 - control_metric_mean) / n)
return ProbabilityDistribution(null_mean, null_std)
def _create_alternative_distribution(
self,
control_metric_mean: float,
treatment_metric_mean: float,
n: int,
) -> ProbabilityDistribution:
alternative_mean = treatment_metric_mean - control_metric_mean
alternative_std = np.sqrt(
treatment_metric_mean * (1 - treatment_metric_mean) / n
+ control_metric_mean * (1 - control_metric_mean) / n
)
return ProbabilityDistribution(alternative_mean, alternative_std)
しかし実はこの実装では、サンプルサイズの公式と一致するような出力を得る事ができませんでした...。:sob:
同様に、non-binary metric版もテストと実装を追加してみたのですが、結果も同様でやや過小な値になってしまいました...。うーん。
オーダー感とか、binary metricとnon-binary metricの大小関係は整合してるんだけど、やや過小な値 (公式の値の3/4くらい??) になってしまうな...:thinking:
- binary metricの方:
- 公式から算出した値: 121599
- 実装から算出した値: 94800
- non-binary metricの方:
- 公式から算出した値: 409600
- 実装から算出した値: 316600
null distributionとalternative distributionが得られた後の検出力の算出処理自体は問題なさそうなので、null distributionとalternative distributionの作り方に違いはありそう?...!:thinking:
(少なくとも公式では、controlとtreatmentに同じ標準偏差を仮定してるし...! でもnon-binary metricの方は、こっちの実装でもcontrolとtreatmentに同じ標準偏差を仮定してるんだよなぁ...:thinking:)
% pytest test_desirable_sample_size_calculation.py
...
========================================================== short test summary info ==========================================================
FAILED test_desirable_sample_size_calculation.py::test_desirable_sample_size_calculation_with_binary_metric - assert (121599 - 1000) <= 94800
FAILED test_desirable_sample_size_calculation.py::test_desirable_sample_size_calculation_with_non_binary_metric - assert (409600 - 1000) <= 316600
============================================================ 2 failed in 10.84s =============================================================
ちなみに、以下はnon-binary metric ver.の単体テストと実装です。
単体テスト:
def test_desirable_sample_size_calculation_with_non_binary_metric() -> None:
# Arrange
significance_level = 0.05
desirable_power = 0.8
## practice論文のsectin 3.2の例に従い、OECを一人当たり収益とする
control_metric_mean = 3.75 # 一人あたり平均3.75ドル
metric_variance = 30**2 # OECの変動性=標準偏差30ドル
treatment_metric_mean = control_metric_mean * (1 + 0.05) # OECの5%の増加を仮定
sut = DesirableSampleSizeSimulatorWithNonBinaryMetric(
significance_level,
desirable_power,
)
# Act
desirable_sample_size_actual = sut.calculate(
control_metric_mean,
treatment_metric_mean,
metric_variance,
)
# Assert
expected = 409600 # 公式より 16 * (30)^2/(3.75 * 0.05)^2
assert expected - 1000 <= desirable_sample_size_actual <= expected + 1000
実装:
class DesirableSampleSizeSimulatorWithNonBinaryMetric:
def __init__(
self,
significance_level: float = 0.05,
desirable_power: float = 0.8,
) -> None:
self.significance_level = significance_level
self.desirable_power = desirable_power
def calculate(
self,
control_metric_mean: float,
treatment_metric_mean: float,
metric_variance: float,
) -> int:
for sample_size in range(100, 10**10, 100):
null_dist = self._create_null_distribution(
control_metric_mean,
metric_variance,
sample_size,
)
alternative_dist = self._create_alternative_distribution(
control_metric_mean,
treatment_metric_mean,
metric_variance,
sample_size,
)
power = calculate_statistical_power(
null_dist,
alternative_dist,
self.significance_level,
AlternativeHypothesisType.GREATER_THAN,
)
if power >= self.desirable_power:
return sample_size
else:
raise ValueError("The desirable sample size is not found. Please re-design the experiment.")
def _create_null_distribution(
self,
control_metric_mean: float,
metric_variance: float,
n: int,
) -> ProbabilityDistribution:
null_mean = control_metric_mean - control_metric_mean
null_std = np.sqrt(2 * metric_variance / n)
return ProbabilityDistribution(null_mean, null_std)
def _create_alternative_distribution(
self,
control_metric_mean: float,
treatment_metric_mean: float,
metric_variance: float,
n: int,
) -> ProbabilityDistribution:
alternative_mean = treatment_metric_mean - control_metric_mean
alternative_std = np.sqrt(2 * metric_variance / n)
return ProbabilityDistribution(alternative_mean, alternative_std)
Discussion