Zenn
😊

Twitterの2-stage推薦の2段階目(candidate ranking)で使われてるっぽいMaskNetの論文を読んだ

2024/01/30に公開
Twitter
#
推薦システム
#
論文要約
#
recommendation
#
maskblock
tech

MaskNet: Introducing Feature-Wise Multiplication to CTR Ranking Models by Instance-Guided Mask

published date: 26 June 2021,
authors: Zhiqiang Wang, Qingyun She, Junlin Zhang
url(paper): https://arxiv.org/abs/2102.07619
(勉強会発表者: morinota)

n週連続推薦システム系論文読んだシリーズ 35 週目の記事になります。
ちなみに34週目は 2種のattentionを用いたニュース推薦タスク用のコンテンツベース手法 NRMS の論文を読んだ! でした!

(特に記載がない限り、各画像は元論文から引用してます:pray:)

どんなもの?

  • きっかけ: 2-stage推薦の2段階目(candidate ranking stage)って、みんなどんなモデルを採用してるんだろうと思った...!
  • twitterの2-stage推薦システム内のrankerモデル(i.e. 2-stage推薦の2ステップ目で使われてるやつ!)として使われているらしい MaskNet の論文。(参考: Heavy Ranker)
  • 特徴量間の相互作用を効果的にモデル化するために、深層学習に基づくCTR予測モデルを拡張するMaskBlockというComponentを提案してる。
    • rankerモデルという用途だけど、結局2値分類タスクとして定式化してる感じ。

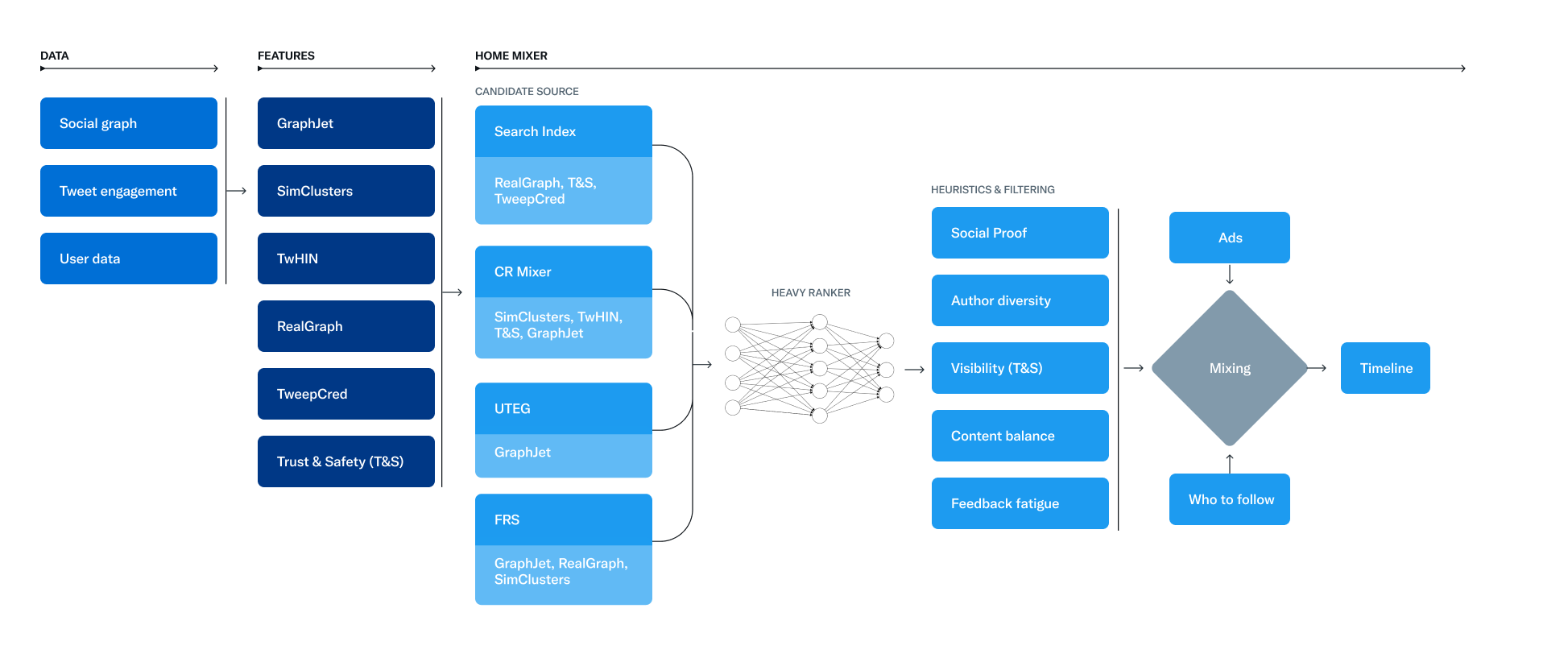
(twitterのリポジトリより引用。上図のheavy rankerの部分でMaskNetを採用してるっぽい)

先行研究と比べて何がすごい？

  • CTR予測タスクは、パーソナライズされた広告配信や推薦システムにおいて重要(主にrankerモデルとしての用途)
    • CTR予測タスクでは、特徴量間の相互作用を効果的にモデル化することが重要な要素らしい。
  • 既存研究:
    • 多くのDNNランキングモデルでは、浅いMLP(Multi Layer Perceptron)層を使って、特徴量間の相互作用を暗黙的にモデル化してる。
      • ex.) FNN(Factorization-machine supported Neural Network), AFM(Attentional Factorization Machine), W&D(Wide & Deep), DeepFM, xDeepFM, etc.
    • -> しかし、複雑な特徴量間の相互作用を捉える上で、feed-forward networkによるadditiveなモデル化だけでは非効率。(Alex Beutel et.al [2])
      • というのも、MLP層は理論的にはあらゆる関数を近似できるが、dot product的な情報を高い精度で学習するには多くの学習データと大きなモデル容量が必要になるから。(らしい...)
    • MLP層以外の手法を使って、additive(加法的)だけでなくmultiplicative(乗法的)に相互作用を捉える手法が提案されてきてる。
  • 本論文のモチベーションは、「DNNランキングモデル(i.e. CTR予測モデル)に特定の乗算演算(multiplicative operation)を導入することで、複雑な特徴量間の相互作用を効率的に捉えられるように改善できないか?」という感じ。
    • 本論文では、feed-forward層に基づくDNNモデルを additive & multiplicativeな特徴量間の相互作用を捉えられるように拡張できるような、MaskBlockという新しいモジュールを提案。
    • またMaskBlockからなるDNNモデルアーキテクチャとして、2種類のMaskNetモデルを提案してる。

技術や手法の肝は？

Instance-Guided Maskについて

MaskBlockの重要な構成要素である Instance Guided Mask についてまとめる。

  • instance-guided maskの役割:
    • 特徴量埋め込み層から出力された全特徴量の情報(=特徴量ベクトル。論文内ではこれをinstanceと定義してる)を活用し、情報量の多い要素を動的に強調すること。
    • また、このcomponentによってDNNランキングモデルに乗算演算を導入している。
  • instance-guided maskの構成(図1)
    • 2つのfully connected(FC)層。
      • 第1FC層は"aggregation layer"。
      • 第2FC層は"projection layer"。

  • instance-guided maskの入力:
    • 特徴量埋め込み層からの出力値(数式にすると以下)
      • ここで、fは特徴量の数、dは特徴量埋め込みの次元数。
      • \mathbf{e}_i \in \mathbb{R}^{k} は1つの特徴量 \mathbf{x}_i に対応する埋め込み表現。
V_{emb} = concat(\mathbf{e}_1, \mathbf{e}_2, \cdots, \mathbf{e}_i, \cdots, \mathbf{e}_{f}) \tag{4}
  • instance-guided maskの振る舞い:
    • 数式に表すと以下。
      • ここで、V_{emb} \in \mathbb{R}^{m = f \times k} は入力インスタンスの埋め込みベクトル。
      • 添字 dは、d番目のinstance-guided maskであることを表す。
      • t と z はそれぞれaggregation layerとprojection layerの出力次元数。
      • W_{d1} \in \mathbb{R}^{t \times m}, W_{d2} \in \mathbb{R}^{z \times t} は、instance-guidedマスクにおけるaggregation layerとprojection layerのパラメータ(投影行列)。同様に \beta_{d1} \in \mathbb{R}^{t}, \beta_{d2} \in \mathbb{R}^{z} は2つのFC層のパラメータ(バイアス項)。
V_{mask} = W_{d2}(Relu(W_{d1} V_{emb} + \beta_{d1})) + \beta_{d2} \tag{5}

  • instance-guided maskのハイパーパラメータ:

    • reduction ratio(縮小率) r:
      • projection layerの出力次元数(i.e. instance-guided maskの出力次元数) z は、後続の特徴量埋め込み層や隠れ層の次元数に合わせて決定される。
      • なのでこの値は、aggregation layerの出力次元数 t をprojection layerと比べてどれくらい大きくするかを決めるために指定する。

  • instance-guided maskの出力値はどう使われる?

    • 後続の特徴量埋め込み層やFFNの隠れ層の出力と組み合わされる。

  • 具体的には、出力値は、後続の特徴量埋め込み層やFFNの隠れ層の出力に対して、アダマール積(element-wise product)による乗算演算を行う。(ここで乗算演算!!)

    • 数式にすると以下:
      • V_{emb} は埋め込み層の出力、V_{hidden} はDNNモデルにおけるFFNの隠れ層の出力
V_{maskedEMB} = V_{mask} \odot V_{emb} \\ V_{maskedHID} = V_{mask} \odot V_{hidden} \tag{6}
  • instance-guided maskの採用による利点:
      1. maskの出力値と、後続の特徴量埋め込み層やFFNの隠れ層の出力とのアダマール積によって、DNNランキングモデル内に統一的な方法で乗算演算が追加される。
      1. instance-guided maskによって得られるbit-wise(特徴量ベクトルにおけるelement-wiseって言っても同義なのかな??:thinking:)のattention的な役割によって、特徴量埋め込み層とFFNにおけるノイズの影響を弱め、DNNランキングモデルにおける有益な信号を強調できる。

MaskBlockについて

本論文では、feed-forward層に基づくDNNモデルを additive & multiplicativeな特徴量間の相互作用を捉えられるように拡張できるような、MaskBlockという新しいモジュールを提案してる。

MaskBlockの主要なcomponentsは以下の3つ:

  • instance-guided mask (これが肝...!)
  • feed-forward hidden layer
  • layer normalization

DNNモデルにおける特徴量埋め込み層やFFN層を、MaskBlockを使って拡張することを想定している。
MaskBlockの使い所は、入力データの違いに応じて2種類に分けられる:

  • MaskBlock on Feature Embedding(図2): 特徴量埋め込み層に対してMaskBlockをくっつけて拡張する。
  • MaskBlock on MaskBlock(図3): 前のMaskBlockの出力を次のMaskBlockの入力として使う。

Layer Normalizationについてメモ

  • MaskBlock内では、instance-guided maskの適用前に**レイヤー正規化(Layer Norm、LN)**を行ってる。
  • 正規化(normalization):
    • 信号がネットワークを伝搬する際に平均値がゼロで分散が単位(=1.0)となるようにし、"covariate(共変量) shift"を減らすことを目的とする。
  • レイヤー正規化(Layer Norm、LN):
    • 入力されたベクトル表現 \mathbf{x} = (x_1, x_2,\cdots, x_{H}) に対して、以下数式のように再中心化(re-centering) & **再スケーリング(re-scaling)**する。
\mathbf{h} = g \odot N(\mathbf{x}) + \mathbf{b} , N(\mathbf{x}) = \frac{\mathbf{x} - \mu}{\delta} \\ \mu = \frac{1}{H} \sum_{i=1}^{H} x_{i} , \delta = \sqrt{\frac{1}{H} \sum_{i=1}^{H} (x_{i} - \mu)^2} \tag{8}

  • ここで、

    • \mathbf{h} はLayerNorm層の出力。
    • \odot はアダマール積。
    • \mu と \delta は入力の平均と標準偏差。
    • バイアス \mathbf{b} とゲイン \mathbf{g} は次元H のパラメータベクトル。
    • (なるほど、LayerNorm層は、入力ベクトルを正規化したあとで線形変換してるのか...!:thinking:)

  • MaskBlockにおけるレイヤー正規化の使い所:

    • 特徴量埋め込み層におけるMaskBlock活用の場合は、式(9)
      • 各特徴量の埋め込み \mathbf{e}_{i} を1つの層とみなしてレイヤー正規化している。
    • DNNモデルのFFN層におけるMaskBlock活用の場合は、式(10)
      • 非線形操作(活性化関数の適用)の前に、レイヤー正規化する。(活性化関数の後にレイヤー正規化することも可能だが、活性化関数の前にレイヤー正規化する方が実験で良かったらしい)
LN_{EMB}(V_{emb}) = concat(LN(\mathbf{e}_1), LN(\mathbf{e}_2),\cdots, LN(\mathbf{e}_{f})) \tag{9}
LN_{HID}(V_{hidden}) = ReLU(LN(W_{i} X)) \tag{10}

MaskBlock on Feature Embedding (特徴量埋め込みをMaskBlockの入力として使うパターン)

  • MaskBlock on Feature Embeddingでは、特徴量埋め込み V_{emb} が唯一の入力値。
  • まず、V_{emb} に対してレイヤー正規化を行う。
  • 続いて、instance-guidedマスクを利用して、V_{emb} の情報量の多い要素をアダマール積で強調する。
    • 数式で表すと以下。V_{maskedEMB} はマスクされた特徴量埋め込み。
    • (instance-guidedマスク V_{mask} を得る為の入力値も、特徴量埋め込み V_{emb} である点に注意。)
V_{maskedEMB} = V_{mask} \odot LN\_EMB(V_{emb}) \tag{11}
  • 最後に、V_{maskedEMB} をFFN層(隠れ層1つ) -> レイヤー正規化 -> 活性化関数に渡して、MaskBlock on Feature Embeddingの出力を得る。
    • 数式で表すと以下。
      • ここで、W_{i} \in \mathbb{R}^{q \times n} は i 番目のMaskBlockにおけるfeed-forward層のパラメータ(=投影行列)、n はV_{maskedEMB} のサイズ、q はFFN層のニューラル数の大きさ(=V_{output} の次元数...??)を表す。
V_{output} = LN_{HID}(W_{i} V_{maskedEMB}) \\ = ReLU(LN(W_i V_{maskedEMB})) \tag{12}

MaskBlock on MaskBlock (前のMaskBlockの出力を次のMaskBlockの入力として使うパターン)

  • このパターンのMaskBlockの入力は、前のMaskBlockの出力 V_{output}^{p} と、特徴量埋め込み V_{emb} の2種類。
    • (instance-guided maskの入力が常に特徴量埋め込み V_{emb} である点に注意。)
  • まず、前のMaskBlockの出力 V_{output}^{p} に対して、instance-guidedマスクの出力とアダマール積を取る。
    • 数式だと以下。
V_{maskedHID} = V_{mask} \odot V_{output}^{p} \tag{13}
  • 続いて、V_{maskedHID} をFFN層(隠れ層1つ) -> レイヤー正規化 -> 活性化関数に渡して、MaskBlock on MaskBlockの出力を得る。
    • 数式で表すと以下。
V_{output} = LN\_HID(W_{i} V_{maskedHID}) \\ = ReLU(LN(W_{i} (V_{mask} \odot V_{output}^{p}))) \tag{14}

二種類のMaskNetモデル

  • MaskBlockをもとに、様々な構成で新しいランキングモデルを設計することができる。MaskBlockで構成されるランクモデルを、本論文ではMaskNetと呼ぶ。
  • 本論文では、MaskBlockを基本構成要素として、2つのMaskNetモデルを提案してる: Serial MaskNet, Parallel MaskNet

Serial MaskNet

  • Serial MaskNet(図4左):
    • (serial=連続, 直列 等の意味:thinking:)
    • MaskBlockを次々に積み重ねて(stackして)ランキングシステムを構築する。
    • 最初のブロックはMaskBlock on Feature Embeddingを使い、以降のブロックはMaskBlock on MaskBlockを使う。
    • prediction層は、最後のMaskBlockの出力ベクトルを入力として受け取る。
    • このモデルでは、全てのMaskBlockにおけるinstance-guided maskの入力は全て特徴量埋め込み層 V_{emb} から渡されるため、Serial MaskNetモデルは各タイムステップで入力を共有するRNNモデルのように見える。(なるへそ...!:thinking:)

Parallel MaskNet

  • Parallel MaskNet(図4右):
    • 特徴量埋め込み層上に、MaskBlocks on feature embedding を複数並列に配置してランキングシステムを構築する。
    • 各MaskBlockの入力は、この構成では共有した特徴量埋め込み V_{emb} のみである。(各MaskedBlockには同じ入力が渡される:thinking:)
    • 各MaskBlockの出力は、prediction層に渡される前にconcatされる。
      • 数式で表すと以下。
        • ここで、V_{output}^{i} は i 番目のMaskBlockの出力。
        • u はMaskBlockの総数、i は i 番目のMaskBlockを表す。
        • q はMaskBlockのFFN層のニューラル数(=出力される埋め込みの次元数:thinking:)
        • (じゃあ V_{merge} \in \mathbb{R}^{uq} になるのかな:thinking:)
V_{merge} = concat(V^{1}_{output}, V^{2}_{output}, \cdots, V^{i}_{output}, \cdots, V^{u}_{output}) \tag{15}
  • 各MaskBlockが捉えた特徴量間の相互作用を更に統合するために、V_{merge} を複数のFFN層に渡す。
    • 数式で表すと以下。
      • H_0 = V_{merge} はFFN層に投入される。(活性化関数がReLUの何層かのfully-connectedのfeed-forward層か。線形変換 ->非線形変換を層の数分繰り返すやつ:thinking:)
      • ここで、l はFFNの深さ。W_{l} \in \mathbb{R}^{q \times q}, \beta_{l} \in \mathbb{R}^{q} は l 番目のFFN層のパラメータ(=投影行列とバイアス項)。
H_{l} = ReLU(W_{l} H_{l-1} + \beta_{l}) \tag{16}
  • 最終的に、FFN層の出力 H_{l} をprediction層に渡して、Parallel MaskNetの出力を得る。

prediction層について

\hat{y} = \delta(w_0 + \sum_{i=1}^{n} w_{i} x_{i}) \tag{17}
  • ここで、
    • \hat{y} \in (0, 1) はCTRの予測値。
    • \delta はsigmoid関数。
    • n は最後のMaskBlockの出力(SerMaskNetの場合) or FFN層の出力(ParaMaskNetの場合)の次元数。
    • x_i は入力の各要素、w_{i} は各要素に対する重み。
    • (最終的な出力をスカラーにしたいからこの層なのね。結局はこれもFFN層:thinking:)

学習方法

  • CTR予測タスクにおいて、損失関数は対数損失(i.e binary cross entropy)を使う。
    • (ランキングモデルといいながらも、結局は2値分類タスクとして定式化してるのか。point-wiseの損失関数でも十分なのかもなぁ、わざわざpair-wiseとかlist-wiseな損失関数を使わなくても...!:thinking:)
\mathcal{L} = - \frac{1}{N} \sum_{i=1}^{N}{ y_i log(\hat{y}_{i}) + (1 - y_i) } \tag{18}

  • ここで、

    • N は学習exampleの数。(=mini-batch1つあたりのtraining exampleの数)
    • y_i は i 番目のexampleの正解ラベル。(click or not click)
    • \hat{y}_{i} は i 番目のexampleの予測CTR値。

  • 実際には正則化項を追加して、以下の損失関数を最適化する。

    • ここで、\lambda は正則化項の強さを決めるハイパーパラメータ。
    • \Theta はモデルのパラメータ集合(特徴量埋め込み行列、instance-guided mask行列、MaskBlockのFFN層、prediction層のパラメータを含む)
L = \mathcal{L} + \lambda ||\Theta|| \tag{19}

どうやって有効だと検証した?

以下の4つのresearch questionsへの回答を目的として、オフライン実験してる。

  • RQ1: MaskBlockに基づく提案手法 MaskNet は、既存のdeep learningベースのCTR予測モデルよりも予測性能が高いか?
  • RQ2: MaskBlockアーキテクチャにおける各Componentsの有効性は? 効果的なランキングシステムを構築するために必要なのか??
  • RQ3: MaskNetのハイパーパラメータはどのように予測性能に影響するか?
  • RQ4: MaskBlock内のInstance-Guided Maskは、入力データに応じて重要な要素を強調できているのか??(i.e. 想定通りに機能してくれているか?)

以下は、オフライン実験の設定:

  • 使用するデータセット達:
    • Criteoデータセット:
      • ユーザへの広告表示とクリックフィードバックからなるデータセット。
    • Malwareデータセット:
      • MicrosoftのMalware予測で公開されたKaggleコンペのデータセット。CTR予測タスクと同様に2値分類タスクとして定式化できるため採用した。
    • Avazuデータセット:
      • Criteo同様に、ユーザへの広告表示とクリックフィードバックからなるデータセット。
  • 学習 & テスト用データの分割方法:
    • training, validation, testの割合は8:1:1で、ランダムにインスタンスを分割した。
    • (時系列に沿ってデータを分割した方が良さそう...!:thinking:)
  • オフライン評価指標:
      1. AUC (そうか、CTR予測タスクだから、必ずしもランキング指標じゃなくてもいいのか:thinking:)
      1. 「RelaImp」= ベースラインモデルに対する相対的なAUCの改善度合い。
      • (数式中の0.5という数値は、random strategyによるAUCの理論値を意味する。)
RelaImp = \frac{AUC(Measured Model) - 0.5}{AUC(Base model) - 0.5} - 1 \tag{20}
  • ベースラインモデル:
    • 既存のdeep learningベースのCTR予測モデル達(FM, DNN, DeepFM, Deep&Cross Network(DCN), xDeepFM, AutoInt Model)
  • 実装の詳細:
    • バッチサイズ=1024, Adam optimizer, learning rate=0.001
    • 全てのモデルでfield embeddingの次元数を10に固定。
    • DNN部分を持つモデルでは、隠れ層の深さを3に固定。1層辺りのニューロン数を400に固定。活性化関数は全てReLUで固定。
    • MaskBlockのハイパーパラメータ:
      • Instance-Guided Maskのreduction ratio(縮小率)を2に固定。

議論はある？

オフライン性能の比較

  • 結果(表2)からわかったこと:
    • (1) Serial MaskNetとParallel MaskNetともに、3つのデータセットでベースラインモデルよりも高い性能を示した。
      • MaskBlockによってDNNモデルに乗算演算を導入したことで、特徴量間の相互作用を効率的に捉えられるようになったから??
    • (2) Serial MaskNetとParallel MaskNetの比較に関して、同程度の性能を示した。
      • MaskBlockが、表現力の高いランキングモデルの構成するために重要なコンポーネントだから??

abration studyによるMaskブロックの各componentsの有効性評価

  • MaskBlockの各componentsの効果を理解するために、MaskBlockの主要componentsであるmask module, レイヤー正規化(LN)、feed forward層(FFN)の有無を変化させたモデルを作成し、オフライン評価を行った。
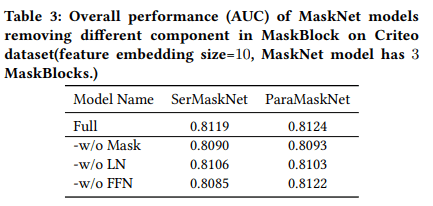
  • 結果(表3)からわかったこと:
    • (1) instance-guided maskとレイヤー正規化のどちらかを削除するとモデルの性能が低下した
      • -> 両componentsはMaskBlockの有効性を高めるために重要な役割を果たしている。
    • (2) feed forward層を削除すると、パラレルモデルでは大きな影響はないが、シリアルモデルでは性能が劇的に低下した。

MaskNetの各ハイパーパラメータの影響評価

  • 1つのハイパーパラメータを変更し、他の設定を維持したまま実験を行った。
  • 特徴量埋め込みの次元数の影響:
    • 次元数を大きくしていくと性能が向上するが、次元数が大きくなりすぎると性能が低下するらしい。
  • MaskBlock数の影響:
    • MaskNetの両モデルについて、MaskBlockを1ブロックから9ブロックまで積み上げる実験を行った。
    • Serial MaskNetでは、5個以上になるまでは性能が向上した。
    • Parallel MaskNetでは、9個にかけて継続的に性能が向上した。
  • instance-guided maskのreduction ratio(縮小率)の影響:
    • instance-guided maskのreduction ratio(縮小率)の影響を探るため、redution ratioを1 ~ 5になるようにaggregate layerの出力次元数を変化させた。
    • reduction ratioはモデルの性能にほとんど影響しなかった。
      • 実際のアプリケーションにおいて計算資源を節約するために、redution ratioを小さくできる可能性。

次に読むべき論文は？

  • うーん、本論文とは全然関係ないけどknowledge-graphとかに関する論文を1つくらい読んでおきたいなぁ...。

Discussion