RustのcandleでMLを勉強する

mochineko

前提とモチベーション

ML の基礎をコードを書いて動かしてちゃんと理解したい
具体的には Torch が自分で使えるくらい
ML、DL の基礎理論や線形代数などの数学の知識はある
Torch その他の ML ライブラリはほとんど触ったことがない
Rust が好き（Python 触るの避けたい）
Hugging Face が開発中の Rust 製 ML ライブラリの candle がサンプルが豊富で面白そう
- Whisper、DINOv2、BERT、 Llama2、Stable-Diffusion、MusicGen など最近のモデルも盛りだくさん
candle は torch Inspired だが、tch-rs と違って Pure Rust で実装されている模様
candle を触りながら ML / DL の基礎を理解し直したい
ただし candle はまだバージョンも切られておらず開発中のステータスなことを留意しておく
- ONNX のサポートがなさそう

mochineko

セットアップ

インストール方法は下記

基本 crate の add をするだけで良いが、CUDA を利用する場合は環境のセットアップが必要。

今回は Docker 環境を nvidia/cuda Image ベースで構築している。

feature flags で下記を有効にしておく・

"cuda"
"cudnn"

"mkl" は Intel CPU、"accelerate" は Apple CPU のスピードアップらしいが GPU 前提なのでいったん追加しないでおく。

mochineko

Hello world の動作確認

まずは公式ドキュメントの Hello world を動かしてみる。

タイトルにはなぜか MNIST の文字が入っているが、シンプルな Neural Network の実装しかない。

一番最初のサンプルコードを写経する。

オリジナルのコードをそのまま動かしてみると実行時にエラーが出る。

Error: WithBacktrace { inner: Cuda(MatMulNonContiguous { lhs_stride: [0, 0], rhs_stride: [0, 0],  ...

MatMulNonContiguous のエラーは、ChatGPT さん曰く Tensor のメモリの並びが不連続の場合に出るエラーらしい。

その原因が CUDA のバージョンなのか何かの設定なのか分からないが、対処自体はシンプルで、Tensorの演算をする際に Tensor.contiguous() を叩いてあげれば良い模様。

ただ、candle-nn の Ready-made な Neural Network を使ったサンプルでも同様のエラーを起こすので、根本的な対応が必要かもしれない。

少なくとも現時点では Issues に関連しそうなものはなさそう。

環境要因の可能性も高そうだが、余裕があれば Issue 立てたほうがいいかも。

mochineko

Linear layer の理解

Hello world の Linear layer のサンプルを写経する。

Lienar layer が何かは下記にまとまっているが、最も基本的な Neural Network の構造。

具体的なコードから何をしているのか理解する。

struct Linear {
    weight: Tensor,
    bias: Tensor,
}

impl Linear {
    fn forward(&self, x: &Tensor) -> Result<Tensor> {
        let x = x.contiguous()?.matmul(&self.weight.contiguous()?)?;
        x.broadcast_add(&self.bias)
    }
}

struct Model {
    first: Linear,
    second: Linear,
}

impl Model {
    fn forward(&self, image: &Tensor) -> Result<Tensor> {
        let x = self.first.forward(image)?;
        let x = x.relu()?;
        self.second.forward(&x)
    }
}

Model は Linear を二つ重ねた構造になっていることが分かる。

let x = self.first.forward(image)?; で一つ目の Linear Layer に通して、 let x = x.relu()?; で ReLU の活性化関数をかけて、self.second.forward(&x) で二つ目の Linear Layer に通している。

Linear Layer の処理は、let x = x.contiguous()?.matmul(&self.weight.contiguous()?)?; で matmul つまり行列の掛け算をして入力値に weight をかけ、x.broadcast_add(&self.bias) で bias（つまり offset）を加えている。

このパラメータ weight と bias を最適化するのが DL の学習という認識。

mochineko

MNIST

CNN（Convolutional Neural Network）の理解のために MNIST を動かしてみる。

CNN の内容は下記を参照する。

CNN 以外のモデルなど不要な部分を取り除いて整理する。

データセットは candle_datasets crate から取得できる。

let dataset = candle_datasets::vision::mnist::load()?;

データセットから Train で使うデータセットと、 Test で使うデータセットをそれぞれ取得する。

// Train dataset
    let train_labels = dateset.train_labels;
    let train_images = dateset
        .train_images
        .to_device(&device)?;
    let train_labels = train_labels
        .to_dtype(DType::U32)?
        .to_device(&device)?;

// Test dataset
    let test_images = dateset
        .test_images
        .to_device(&device)?;
    let test_labels = dateset
        .test_labels
        .to_dtype(DType::U32)?
        .to_device(&device)?;

.to_device(&device) はおそらくデータを GPU にコピーしている処理。

モデルの用意をする。

 // Model
    let mut var_map = VarMap::new();
    let var_builder_args =
        VarBuilder::from_varmap(&var_map, DType::F32, &device);
    let model = ConvolutionalNetwork::new(var_builder_args.clone())?;
    if let Some(load) = &args.load {
        println!("loading weights from {load}");
        var_map.load(load)?
    }

モデルの構造を詳しく見てみる、まずはパラメータ。

#[derive(Debug)]
struct ConvolutionalNetwork {
    conv1: Conv2d,
    conv2: Conv2d,
    fc1: Linear,
    fc2: Linear,
}

impl Model for ConvolutionalNetwork {
    fn new(vs: VarBuilder) -> Result<Self> {
        let conv1 = candle_nn::conv2d(
            1,
            32,
            5,
            Default::default(),
            vs.pp("c1"),
        )?;
        let conv2 = candle_nn::conv2d(
            32,
            64,
            5,
            Default::default(),
            vs.pp("c2"),
        )?;
        let fc1 = candle_nn::linear(1024, 1024, vs.pp("fc1"))?;
        let fc2 = candle_nn::linear(1024, LABELS, vs.pp("fc2"))?;
        Ok(Self {
            conv1,
            conv2,
            fc1,
            fc2,
        })
    }
}

conv1 の設定は下記。

in_channels = 1
out_channels = 32
kernel_size = 5

conv2 の設定は下記。

in_channels = 32
out_channels = 64
kernel_size = 5

fc1 の設定は下記。

in_dim = 1024
out_dim = 1024

fc2 の設定は下記。

in_dim = 1024
out_dim = 10（ラベル数）

fc2 を最後に適用するので出力データは 10 次元（＝ラベル数）。

二次元の CNN Layer conv2d が二種類、Linear Layer Linear が二種類で構成されている。

impl Model for ConvolutionalNetwork {
     fn forward(
        &self,
        xs: &Tensor,
    ) -> Result<Tensor> {
        let (batch_size, _image_dimension) = xs.dims2()?;
        xs.reshape((batch_size, 1, 28, 28))?
            .apply(&self.conv1)?
            .max_pool2d(2)?
            .apply(&self.conv2)?
            .max_pool2d(2)?
            .flatten_from(1)?
            .apply(&self.fc1)?
            .relu()?
            .apply(&self.fc2)
    }
}

forward() の実装を詳しく追ってみる。

xs.reshape((batch_size, 1, 28, 28))?: 四次元の Tensor、28 * 28 のグレースケールの画像に整形
.apply(&self.conv1): 一つ目の CNN Layer の適用
.max_pool2d(2): 一つ目の Pooling Layer の適用をして圧縮
.apply(&self.conv2): 二つ目の CNN Layer の適用
.max_pool2d(2): 二つ目の Pooling Layer の適用をして圧縮
.flatten_from(1): 一次元のベクトルに平坦化
.apply(&self.fc1): 一つ目の Linear Layer の適用
.relu(): ReLU 活性化関数の適用
.apply(&self.fc2): 二つ目の Linear Layer の適用

参考記事でも紹介されている典型的な CNN の構造で、コードでの対応を確認できた。

次にこの CNN を使った学習のコードを見てみる。

まずは最適化アルゴリズム optimizer の部分。

    // Optimizer
    let adamw_params = candle_nn::ParamsAdamW {
        lr: args.learning_rate,
        ..Default::default()
    };
    let mut optimizer =
        candle_nn::AdamW::new(var_map.all_vars(), adamw_params)?;

具体的なアルゴリズムはデファクトスタンダードの Adam を使用している。

最適化アルゴリズムの説明は下記を参照。

epoch を回して学習する部分の Train phase を見てみる。

        let mut sum_loss = 0f32;
        batch_indices.shuffle(&mut thread_rng());

        // Train phase
        for batch_index in batch_indices.iter() {
            let train_images =
                train_images.narrow(0, batch_index * BSIZE, BSIZE)?;
            let train_labels =
                train_labels.narrow(0, batch_index * BSIZE, BSIZE)?;
            let logits = model.forward(&train_images)?;
            let log_softmax = ops::log_softmax(&logits, D::Minus1)?;
            let loss = loss::nll(&log_softmax, &train_labels)?;
            optimizer.backward_step(&loss)?;
            sum_loss += loss.to_vec0::<f32>()?;
        }
        let avg_loss = sum_loss / batches as f32;

まず batch_indices.shuffle(&mut thread_rng()); でバッチ処理のインデックスをシャッフルして順番がランダムになるようにしている。

let logits = model.forward(&train_images)?; で CNN に画像データを通しているが、logit というのは NN の生の出力値のことらしい。

let log_softmax = ops::log_softmax(&logits, D::Minus1)?; は活性化関数として log (Softmax) を使用している。

let loss = loss::nll(&log_softmax, &train_labels)?; で NLL Loss を計算している。

やっていることは Cross Entropy Loss と同等らしい。

loss が計算できたら optimizer.backward_step(&loss)?; で Backpropagation に通して現在のパラメータでの loss の結果を元にモデルのパラメータを更新する。

optimizer を通して model のパラメータが更新されている？（内部の挙動ちゃんと確認したい）

Test phase ではテスト用のデータを実際に通してみて正答率を計算する。

        // Test phase
        let test_logits = model.forward(&test_images)?;
        let sum_ok = test_logits
            .argmax(D::Minus1)?
            .eq(&test_labels)?
            .to_dtype(DType::F32)?
            .sum_all()?
            .to_scalar::<f32>()?;
        let test_accuracy = sum_ok / test_labels.dims1()? as f32;

.argmax(D::Minus1) は test_logitsが各ラベルの評価値になっているので、その中から最大のラベルを取り出している操作。

これで CNN の学習の具体的な実行内容がコードで理解できた。

mochineko

Linear
CNN

の次は RNN か Transformer のサンプルを見たいところだが、candle-transformers の中身は空で candle-nn にも実装がなさそう。

RNN は candle-nn に実装があるがサンプルコードがどこにあるのかわからない。

すると candle-examples から次に触る比較的シンプルなものを選びたい。

Whisper: speech recognition model.
LLaMA and LLaMA-v2: general LLM.
Falcon: general LLM.
Bert: useful for sentence embeddings.
StarCoder: LLM specialized to code generation.
Stable Diffusion: text to image generative model, support for the 1.5, 2.1, and SDXL 1.0 versions.
DINOv2: computer vision model trained using self-supervision (can be used for imagenet classification, depth evaluation, segmentation).
Quantized LLaMA: quantized version of the LLaMA model using the same quantization techniques as llama.cpp.
yolo-v3 and yolo-v8: object detection and pose estimation models.

yolo-v3、Falcon あたりがシンプルで触りやすそう。

mochineko

YOLO v3 / v8

思っていたよりちゃんとしたアーキテクチャなので流石に全部追うのは時間の無駄か。

CNN も一応理解はできてはいるので、動作確認だけしてみたい。

mochineko

やっぱりテキスト系の Transformer ベースモデルが触りたいので、LLaMA の実装を見ることにする。

Transformer の解説を見ながらどの部分のコードを読むか当たりをつける。

内部で使われている flash-attn というのは flash-attention という最適化された Attention の実装らしい。

LLaMA のモデルの全体像の実装は下記。

pub struct Llama {
    wte: Embedding,
    blocks: Vec<Block>,
    ln_f: RmsNorm,
    lm_head: Linear,
}

impl Llama {
    pub fn forward(&self, x: &Tensor, index_pos: usize) -> Result<Tensor> {
        let (_b_sz, seq_len) = x.dims2()?;
        let mut x = self.wte.forward(x)?;
        for (block_idx, block) in self.blocks.iter().enumerate() {
            x = block.forward(&x, index_pos, block_idx)?;
        }
        let x = self.ln_f.forward(&x)?;
        let x = x.i((.., seq_len - 1, ..))?;
        let logits = self.lm_head.forward(&x)?;
        logits.to_dtype(DType::F32)
    }

    ...
}

見慣れない単語があるので LLaMA の解説を見る。

https://toukei-lab.com/llama

RmsNorm は RMS(Root Mean Square) Normalization のことらしい。

apply_rotary_emb は相対的な Positional Encoding のことらしい。

Embedding は candle_nn に実装があるが、ちゃんと理解できてないので調べる。

mochineko

Embedding Layer をちゃんと理解する。

forward で何をしているのかを理解する。

impl crate::Module for Embedding {
    fn forward(&self, indexes: &Tensor) -> Result<Tensor> {
        let mut final_dims = indexes.dims().to_vec();
        final_dims.push(self.hidden_size);
        let indexes = indexes.flatten_all()?;
        let values = self.embeddings.index_select(&indexes, 0)?;
        let values = values.reshape(final_dims)?;
        Ok(values)
    }
}

let mut final_dims = indexes.dims().to_vec(); は、入力の indexes （indices ではない？）の次元数を計算している。

final_dims.push(self.hidden_size); は hidden_size の次元を加えていることになる。

hidden_size は Embedding のベクトルの次元数。

let indexes = indexes.flatten_all()?; で一次元に並べて、 let values = self.embeddings.index_select(&indexes, 0)? で値を取り出して、 let values = values.reshape(final_dims)?; で再度 Tensor の形に戻している。

例えばテキストを Embedding に変換する例だと、入力の indexes は Tokenizer でトークン化（hidden_size の Dictionary の対応するインデックスに変換する）されたテキストの配列に対応する。

そのトークンの配列を内部のベクトル表現の配列に変換し、Tensor として出力する。

mochineko

Block が Transformer 内のブロック構造の実装になっているので詳しく見てみる。

struct Block {
    rms_1: RmsNorm,
    attn: CausalSelfAttention,
    rms_2: RmsNorm,
    mlp: Mlp,
    span: tracing::Span,
}

impl Block {
    fn forward(&self, x: &Tensor, index_pos: usize, block_idx: usize) -> Result<Tensor> {
        let _enter = self.span.enter();
        let residual = x;
        let x = self.rms_1.forward(x)?;
        let x = (self.attn.forward(&x, index_pos, block_idx)? + residual)?;
        let residual = &x;
        let x = (self.mlp.forward(&self.rms_2.forward(&x)?)? + residual)?;
        Ok(x)
    }

    ...
}

let residual = x; で入力の Tensor を保持している。

let x = self.rms_1.forward(x)?; で RMS の正則化をかけている。

self.attn.forward(&x, index_pos, block_idx)? で Causal Self Attention に通している。（要確認）

let x = (self.attn.forward(&x, index_pos, block_idx)? + residual)?; で Attention の結果と元の入力を足している。（Residual Connection）

&self.rms_2.forward(&x)? で二回目の RMS正則化をかけている。

self.mlp.forward(&self.rms_2.forward(&x)?)? で MLP（Muti-layer perceptron）にかけている。（要確認）

let x = (self.mlp.forward(&self.rms_2.forward(&x)?)? + residual)?; で MLP の結果を再度 Residual Connection している。

↓

有名なあの図の入力から Add & Norm に伸びている矢印が Residual Connection で、Norm の処理が LLaMA だと RMS Norm で、コアの部分が Attention になっている、という理解。

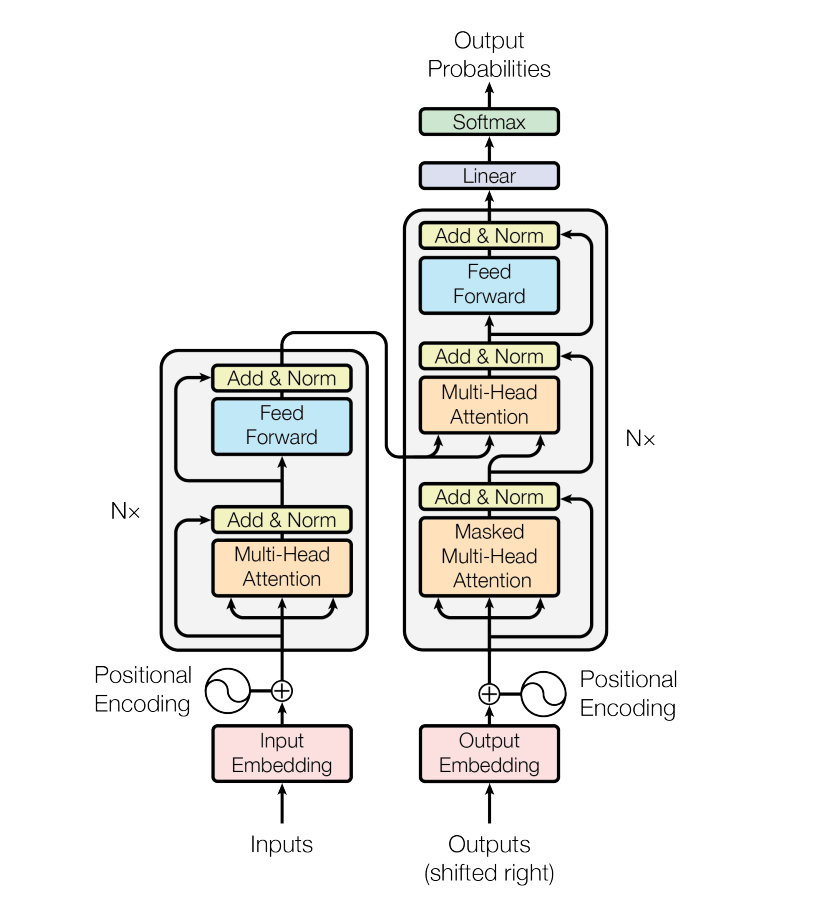
Causal Self Attention と NLP がまだちゃんと理解できていないので詳しく見てみる。

mochineko

MLP は図で言う Feed Foward の部分に対応する模様。

厳密には定義は違うみたいだが。

https://hayashibe.jp/note/ml/dl/ffnn

struct Mlp {
    c_fc1: Linear,
    c_fc2: Linear,
    c_proj: Linear,
    span: tracing::Span,
}

impl Mlp {
    fn forward(&self, x: &Tensor) -> Result<Tensor> {
        let _enter = self.span.enter();
        let x = (candle_nn::ops::silu(&self.c_fc1.forward(x)?)? * self.c_fc2.forward(x)?)?;
        self.c_proj.forward(&x)
    }

   ...
}

struct の定義から三つの Linear Layer で構成されている。

forward では &self.c_fc1.forward(x)? で c_fc1 の Linear Layer に通して SiLU（Sigmoid Linear Unit）に通した結果と、self.c_fc2.forward(x)? で c_fc2 の Linear Layer に通した結果とを掛け算している。

この掛け算は行列の掛け算ではなく要素同士の掛け算（Element-wise Multiplication）らしい。

最後に self.c_proj.forward(&x) で Down Projection Layer に通して次元を落としている。

この MLP の具体的な特性までは理解できていないが、構造としてはシンプルなので把握はできた。

mochineko

Attention を見る前に忘れていた Positional Encoding の部分を確認しておく。

impl CausalSelfAttention {
    fn apply_rotary_emb(&self, x: &Tensor, index_pos: usize) -> Result<Tensor> {
        let _enter = self.span_rot.enter();
        let (b_sz, _, seq_len, hidden_size) = x.dims4()?;
        let cos = self.cache.cos.narrow(0, index_pos, seq_len)?;
        let sin = self.cache.sin.narrow(0, index_pos, seq_len)?;
        let cos = cos.broadcast_as((b_sz, 1, seq_len, hidden_size))?;
        let sin = sin.broadcast_as((b_sz, 1, seq_len, hidden_size))?;
        let x1 = x.narrow(D::Minus1, 0, hidden_size / 2)?;
        let x2 = x.narrow(D::Minus1, hidden_size / 2, hidden_size / 2)?;
        let rotate_x = Tensor::cat(&[&x2.neg()?, &x1], D::Minus1)?;
        let rope = (x.broadcast_mul(&cos)? + rotate_x.broadcast_mul(&sin)?)?;
        Ok(rope)
    }
    ...
}

入力の Embedding に対して、Rotary Positional Embedding を適用している。

つまりテキストの相対位置の情報を埋め込んで、位置（時系列）の情報を学習して反応するようにしている。

具体的に使用している箇所を見ると、どうやら入力のテキストではなく Attention の内部で Query、Key、Value それぞれに Rotary Positional Embedding を適用しているよう。

        let q = self.apply_rotary_emb(&q, index_pos)?;
        let mut k = self.apply_rotary_emb(&k, index_pos)?;

一度だけ適用するより時系列の影響が強くなりそうな雰囲気は感じるが、ちゃんと理解できてはいない。

mochineko

いよいよ Attention の本体を見ていく。

長いのでまずは struct 部分から。

struct CausalSelfAttention {
    q_proj: Linear,
    k_proj: Linear,
    v_proj: Linear,
    o_proj: Linear,
    num_attention_heads: usize,
    num_key_value_heads: usize,
    head_dim: usize,
    cache: Cache,
    use_flash_attn: bool,
    span: tracing::Span,
    span_rot: tracing::Span,
}

q_proj: Linear
k_proj: Linear
v_proj: Linear
o_proj: Linear

の四つは Attention 構造の Query、Key、Value、Output を取り出す Linear Layer。

forward の処理を見てみる。

impl CausalSelfAttention {
    ...

    fn forward(&self, x: &Tensor, index_pos: usize, block_idx: usize) -> Result<Tensor> {
        let _enter = self.span.enter();
        let (b_sz, seq_len, hidden_size) = x.dims3()?;
        let q = self.q_proj.forward(x)?;
        let k = self.k_proj.forward(x)?;
        let v = self.v_proj.forward(x)?;

        let q = q
            .reshape((b_sz, seq_len, self.num_attention_heads, self.head_dim))?
            .transpose(1, 2)?;
        let k = k
            .reshape((b_sz, seq_len, self.num_key_value_heads, self.head_dim))?
            .transpose(1, 2)?;
        let mut v = v
            .reshape((b_sz, seq_len, self.num_key_value_heads, self.head_dim))?
            .transpose(1, 2)?;

        let q = self.apply_rotary_emb(&q, index_pos)?;
        let mut k = self.apply_rotary_emb(&k, index_pos)?;

        if self.cache.use_kv_cache {
            let mut cache = self.cache.kvs.lock().unwrap();
            if let Some((cache_k, cache_v)) = &cache[block_idx] {
                k = Tensor::cat(&[cache_k, &k], 2)?.contiguous()?;
                v = Tensor::cat(&[cache_v, &v], 2)?.contiguous()?;
                let k_seq_len = k.dims()[1];
                if k_seq_len > MAX_SEQ_LEN {
                    k = k
                        .narrow(D::Minus1, k_seq_len - MAX_SEQ_LEN, MAX_SEQ_LEN)?
                        .contiguous()?
                }
                let v_seq_len = v.dims()[1];
                if v_seq_len > 2 * MAX_SEQ_LEN {
                    v = v
                        .narrow(D::Minus1, v_seq_len - MAX_SEQ_LEN, MAX_SEQ_LEN)?
                        .contiguous()?
                }
            }
            cache[block_idx] = Some((k.clone(), v.clone()))
        }

        let k = self.repeat_kv(k)?;
        let v = self.repeat_kv(v)?;

        let y = if self.use_flash_attn {
            // flash-attn expects (b_sz, seq_len, nheads, head_dim)
            let q = q.transpose(1, 2)?;
            let k = k.transpose(1, 2)?;
            let v = v.transpose(1, 2)?;
            let softmax_scale = 1f32 / (self.head_dim as f32).sqrt();
            flash_attn(&q, &k, &v, softmax_scale, seq_len > 1)?.transpose(1, 2)?
        } else {
            let in_dtype = q.dtype();
            let q = q.to_dtype(DType::F32)?;
            let k = k.to_dtype(DType::F32)?;
            let v = v.to_dtype(DType::F32)?;
            let att = (q.matmul(&k.t()?)? / (self.head_dim as f64).sqrt())?;
            let mask = self.cache.mask(seq_len)?.broadcast_as(att.shape())?;
            let att = masked_fill(&att, &mask, f32::NEG_INFINITY)?;
            let att = candle_nn::ops::softmax(&att, D::Minus1)?;
            // Convert to contiguous as matmul doesn't support strided vs for now.
            att.matmul(&v.contiguous()?)?.to_dtype(in_dtype)?
        };
        let y = y.transpose(1, 2)?.reshape(&[b_sz, seq_len, hidden_size])?;
        let y = self.o_proj.forward(&y)?;
        Ok(y)
    }
    ...
}

let v = self.repeat_kv(v)?; までの前半部分は大雑把に言えば Query、Key、Value をそれぞれ計算しているだけ。

前述した Rotary Positional Embedding も適用している。

キャッシュを使って計算コストを削減したり、Tensor の形を整えたりもしている。

Attention の具体の実装は flash-attention を使うかの分岐が入っているが、いったん愚直な実装の方を見てみる。

            let att = (q.matmul(&k.t()?)? / (self.head_dim as f64).sqrt())?;
            let mask = self.cache.mask(seq_len)?.broadcast_as(att.shape())?;
            let att = masked_fill(&att, &mask, f32::NEG_INFINITY)?;
            let att = candle_nn::ops::softmax(&att, D::Minus1)?;
            // Convert to contiguous as matmul doesn't support strided vs for now.
            att.matmul(&v.contiguous()?)?.to_dtype(in_dtype)?

let att = (q.matmul(&k.t()?)? / (self.head_dim as f64).sqrt())?; で Query と Key の matmal（＝内積）を計算して次元数でスケーリングしている。

let mask = self.cache.mask(seq_len)?.broadcast_as(att.shape())?; と let att = masked_fill(&att, &mask, f32::NEG_INFINITY)?; で未来の情報などのマスクを-∞で適用している。

let att = candle_nn::ops::softmax(&att, D::Minus1)?; で Softmax 関数を適用している。

最後に att.matmul(&v.contiguous()?)?.to_dtype(in_dtype)? で Softmax の結果と Value の内積を計算している。

こうしてみるとよく見るあの数式

Attention(Q, K, V ) = softmax\Bigl(\frac{QK^T}{\sqrt{d_k}}\Bigr)V

で Query と Key の内積を $\sqrt{d_k}$ でスケーリングして Softmax したものと Value との内積を取る、という操作がちゃんとコードと対応して理解できる。

mochineko

ここまでで LLaMA の構造のパーツが一通り理解できたはずなので、改めて全体の流れを確認してみる。

あと改めて Attention is all you need の論文の解説も読み返したい。

mochineko

LLaMA の内部処理の流れを整理する。

入力テキストを Tokenizer でトークンの配列にエンコードする

let mut tokens = tokenizer
    .encode(prompt, true)
    .map_err(E::msg)?
    .get_ids()
    .to_vec();

トークンの配列を Embedding Layer（Word Token Embedding、Sentence Embedding）に渡してトークンを Embedding（トークンのベクトル表現）の配列、つまり Tensor に変換する

let mut x = self.wte.forward(x)?;

Transformer のいくつかの Block に通す

for (block_idx, block) in self.blocks.iter().enumerate() {
    x = block.forward(&x, index_pos, block_idx)?;
}

Transformer の結果を RMS Norm で正規化し、全結合 Layer に通して結果を返す

let x = self.ln_f.forward(&x)?;
let x = x.i((.., seq_len - 1, ..))?;
let logits = self.lm_head.forward(&x)?;

Block の内部処理も確認する。

RMS Norm で正規化して Attention を適用する
Residual Connection を適用する
RMS Norm で正規化して MLP（Feed Forward）を適用する
Residual Connection を適用する

let residual = x;
let x = self.rms_1.forward(x)?;
let x = (self.attn.forward(&x, index_pos, block_idx)? + residual)?;
let residual = &x;
let x = (self.mlp.forward(&self.rms_2.forward(&x)?)? + residual)?;

Attention の内部処理も確認する。

入力 Tensor に Linear Layer を通して Query、Key、Value を計算し、それぞれに Rotary Positional Embedding で位置情報を埋め込む

        let q = self.q_proj.forward(x)?;
        let k = self.k_proj.forward(x)?;
        let v = self.v_proj.forward(x)?;

        let q = q
            .reshape((b_sz, seq_len, self.num_attention_heads, self.head_dim))?
            .transpose(1, 2)?;
        let k = k
            .reshape((b_sz, seq_len, self.num_key_value_heads, self.head_dim))?
            .transpose(1, 2)?;
        let mut v = v
            .reshape((b_sz, seq_len, self.num_key_value_heads, self.head_dim))?
            .transpose(1, 2)?;

        let q = self.apply_rotary_emb(&q, index_pos)?;
        let mut k = self.apply_rotary_emb(&k, index_pos)?;

        if self.cache.use_kv_cache {
            let mut cache = self.cache.kvs.lock().unwrap();
            if let Some((cache_k, cache_v)) = &cache[block_idx] {
                k = Tensor::cat(&[cache_k, &k], 2)?.contiguous()?;
                v = Tensor::cat(&[cache_v, &v], 2)?.contiguous()?;
                let k_seq_len = k.dims()[1];
                if k_seq_len > MAX_SEQ_LEN {
                    k = k
                        .narrow(D::Minus1, k_seq_len - MAX_SEQ_LEN, MAX_SEQ_LEN)?
                        .contiguous()?
                }
                let v_seq_len = v.dims()[1];
                if v_seq_len > 2 * MAX_SEQ_LEN {
                    v = v
                        .narrow(D::Minus1, v_seq_len - MAX_SEQ_LEN, MAX_SEQ_LEN)?
                        .contiguous()?
                }
            }
            cache[block_idx] = Some((k.clone(), v.clone()))
        }

        let k = self.repeat_kv(k)?;
        let v = self.repeat_kv(v)?;

Query と Key（の転置）の内積を Head の次元のルートで割る

let att = (q.matmul(&k.t()?)? / (self.head_dim as f64).sqrt())?;

Mask 処理をする

let mask = self.cache.mask(seq_len)?.broadcast_as(att.shape())?;
let att = masked_fill(&att, &mask, f32::NEG_INFINITY)?;

Sofmax を適用する

let att = candle_nn::ops::softmax(&att, D::Minus1)?;

Value との内積を取る

att.matmul(&v.contiguous()?)?.to_dtype(in_dtype)?

mochineko

LLaMA で Transformer が理解できたような気がするので、Whisper や Stable Diffusion など他の Transformer（Attention）ベースのモデルも見てみたい。

mochineko

MMPose を触ってみたいがコード量多そうなので書き直すのがしんどそう。

https://github.com/open-mmlab/mmpose

mochineko

最近お世話になっている Whisper の candle 実装を追ってみる。

Whisper の解説は下記を参考にする。

pub struct Whisper {
    pub encoder: AudioEncoder,
    pub decoder: TextDecoder,
    pub config: Config,
}

Whisper は入力が音声、出力がテキストなので基本構成は AudioEncoder と TextDecoder。

推論の処理は main.rs の Decoder を追うのが良さそう。

mochineko

AudioEncoder を見ていく。

pub struct AudioEncoder {
    conv1: Conv1d,
    conv2: Conv1d,
    positional_embedding: Tensor,
    blocks: Vec<ResidualAttentionBlock>,
    ln_post: LayerNorm,
    span: tracing::Span,
    conv1_span: tracing::Span,
    conv2_span: tracing::Span,
}

Conv1d（CNN）が二つあるのはアーキテクチャ図の「2 × Conv1D」の部分に対応する。

positional_embedding は「Sinusoidal Positiona Encoding」の処理だが Sin 関数を使った Positional Encoding のことらしい。

blocks は LLaMA でも見た Attention + MLP のブロック構造からなる Transformer の部分。

ln_post は出力を正規化する Layer 。

forward の実際の処理を見てみる。

impl AudioEncoder {
    ...

    pub fn forward(&mut self, x: &Tensor, flush_kv_cache: bool) -> Result<Tensor> {
        let _enter = self.span.enter();
        let x = {
            let _enter = self.conv1_span.enter();
            self.conv1.forward(x)?.gelu()?
        };
        let x = {
            let _enter = self.conv2_span.enter();
            self.conv2.forward(&x)?.gelu()?
        };
        let x = x.transpose(1, 2)?;
        let (_bsize, seq_len, _hidden) = x.dims3()?;
        let positional_embedding = self.positional_embedding.narrow(0, 0, seq_len)?;
        let mut x = x.broadcast_add(&positional_embedding)?;
        for block in self.blocks.iter_mut() {
            x = block.forward(&x, None, None, flush_kv_cache)?
        }
        let x = self.ln_post.forward(&x)?;
        Ok(x)
    }
}

入力は Log-Mel Spectrogram なので離散的な分布 = 行列（Tensor）になる。

最初の二つの let x = ... で二つの Conv1D と GELU 活性化関数を適用している。

let mut x = x.broadcast_add(&positional_embedding)?; が Positional Encoding をしている部分。

for block in self.blocks.iter_mut() { ... } で各Block に通して、最後に let x = self.ln_post.forward(&x)?; で正規化して結果を出力する。

Encoding はアーキテクチャの通りで LLaMA で慣れている分すんなり理解できる。

やっていることとしては、Log-Mel Spectrogram の音声データを CNN + Positional Encoding + Transformer に通してその音声の特徴を抽出しているということ。

この結果を利用して次の TextDecoder でテキストを生成していく。

入力の手前の Log-Mel Spectrogram の変換周りも後で確認する。

mochineko

TextDecoder を見ていく。

pub struct TextDecoder {
    token_embedding: Embedding,
    positional_embedding: Tensor,
    blocks: Vec<ResidualAttentionBlock>,
    ln: LayerNorm,
    mask: Tensor,
    span: tracing::Span,
    span_final: tracing::Span,
}

token_embedding は生成するテキストのトークンの Embedding Layer。

positional_embedding は Learned（学習済み）Positional Encoding。

blocks は Transformer のブロック構造だが、Encoder と同じ ResidualAttentionBlock になっている。（図だとちょっと違うように見えるがなぜ？）

ln、mask も例のごとく。

forward の処理も見ていく。

impl TextDecoder {
    ...

    pub fn forward(&mut self, x: &Tensor, xa: &Tensor, flush_kv_cache: bool) -> Result<Tensor> {
        let _enter = self.span.enter();
        let last = x.dim(D::Minus1)?;
        let token_embedding = self.token_embedding.forward(x)?;
        let positional_embedding = self.positional_embedding.narrow(0, 0, last)?;
        let mut x = token_embedding.broadcast_add(&positional_embedding)?;
        for block in self.blocks.iter_mut() {
            x = block.forward(&x, Some(xa), Some(&self.mask), flush_kv_cache)?;
        }
        self.ln.forward(&x)
    }

    ...
}

x はテキストのトークン配列、xa はエンコード済みの音声の Embedding に対応しているよう。

let token_embedding = self.token_embedding.forward(x)?; でトークン配列を Embeddings の Tensor に変換する。

let mut x = token_embedding.broadcast_add(&positional_embedding)?; で Positional Encoding をする。

for block in self.blocks.iter_mut() { ... } で各 Block に通すが、よく見ると第二・第三引数が AudioEncoding と変わっているから一つの struct で両方とも対応しているよう、納得。

最後は self.ln.forward(&x) で正規化して出力している。

ResidualAttensionBlock が少し LLaMA と変わっていたり、Cross Attention が何かちゃんと理解できていないのでちゃんと確認する。

mochineko

ResidualAttentionBlock の中身を詳しく見ていく。

struct ResidualAttentionBlock {
    attn: MultiHeadAttention,
    attn_ln: LayerNorm,
    cross_attn: Option<(MultiHeadAttention, LayerNorm)>,
    mlp_linear1: Linear,
    mlp_linear2: Linear,
    mlp_ln: LayerNorm,
    span: tracing::Span,
}

attn は Self Attention、attn_ln は正規化、cross_attn は Cross Attention（同じ Multi -head attention だが何か差分はある？）、残りは MLP の構成要素。

impl ResidualAttentionBlock {
    ...

    fn forward(
        &mut self,
        x: &Tensor,
        xa: Option<&Tensor>,
        mask: Option<&Tensor>,
        flush_kv_cache: bool,
    ) -> Result<Tensor> {
        let _enter = self.span.enter();
        let attn = self
            .attn
            .forward(&self.attn_ln.forward(x)?, None, mask, flush_kv_cache)?;
        let mut x = (x + attn)?;
        if let Some((attn, ln)) = &mut self.cross_attn {
            x = (&x + attn.forward(&ln.forward(&x)?, xa, None, flush_kv_cache)?)?;
        }
        let mlp = self.mlp_linear2.forward(
            &self
                .mlp_linear1
                .forward(&self.mlp_ln.forward(&x)?)?
                .gelu()?,
        )?;
        x + mlp
    }
}

        let attn = self
            .attn
            .forward(&self.attn_ln.forward(x)?, None, mask, flush_kv_cache)?;

で正規化してから Self Attention に Mask を適用しつつ通す。

let mut x = (x + attn)?; は Residual Connection。

Decoder では x = (&x + attn.forward(&ln.forward(&x)?, xa, None, flush_kv_cache)?)?; で Cross Attention も適用している、こちらは Mask なし。

MLP は書き方は違うが LLaMA と同様。

x + mlp は Residual Connection。

Cross Attention 以外は LLaMA とあまり変わらず。

mochineko

MultiHeadAttention は長そうなのでポイントだけ見ていく。

struct MultiHeadAttention {
    query: Linear,
    key: Linear,
    value: Linear,
    out: Linear,
    n_head: usize,
    span: tracing::Span,
    softmax_span: tracing::Span,
    matmul_span: tracing::Span,
    kv_cache: Option<(Tensor, Tensor)>,
}

Query、Key、Value、Output はいつもの通り。

reshape_head で小さい Head に分割され、Output の Linear Layer で連結されるのが Multi-Head の特徴。

Query は必ず x、つまりテキストの Attention から計算されるが、let (k, v) = match xa { ... } の分岐があるので、xa の指定がある場合は Key と Value は xa から、つまり音声の Attention から計算されるのが Cross Attention の特徴。

入力は音声だけど出力がテキストと形式が異なるので、Encoder-Decoder で Cross-Attention させることで互いの影響を混ぜているという理解。

mochineko

これで Whisper モデルの内部処理はおおよそ理解できたので、あとは入出力周りの Log Mel や結果のトークン配列の変換周り、マルチタスク（Transcribe と Translate の切り替え）周りも確認しておきたい。

mochineko

main.rs の Decoder で最終的には let text = self.tokenizer.decode(&tokens, true).map_err(E::msg)?; でトークンをテキストに変換している。

Log Mel の実装は audio.rs にある。

Log Mel の具体の理解もまだなのでちゃんと確認しておく。

マルチタスクはアーキテクチャの図にあるように、テキストのトークン配列を生のテキストだけじゃなくて言語やタスクの種類などの特殊なトークンを埋め込むという仕組みのよう、理解。

mochineko

Log-Mel Spectrogram を理解する。

Mel Scale

Mel Scale の定義は下記。

m(f) = m_0 \log_{10} ( 1 + \frac{f}{f_0} )

$f / f_0 << 1$ の場合、 $log(1 + f / f_0) \approx f / f_0$ なので

m(f) \approx m_0\ \frac{f}{f_0}

と近似できるので、低周波数帯では線形、高周波数帯では Log の振る舞いをすることが分かる。

逆変換は下記。

f(m) = f_0( 10^{m/m_0} - 1 )

$m_0$ は 1000 Mel = 1000 Hz の拘束条件から決まる。

m_0 = \frac{1000}{ \log_{10} ( 1 + \frac{1000\mathrm{Hz}}{f_0} )}

一般的に用いられるパラメータは $f_0 = 700, m_0 = 2595$ 。

メル尺度は基底膜上の座標とほとんど一致します。1000メルは基底膜の1cmに相当し、臨界帯域幅は約137メルに相当します。

というのはいかにも Deep Learning っぽい。

Mel Spectrogram

Spectrum は波形 $x(t)$ のフーリエ変換 $X(f)$

X(f) = \int dt w(t) x(t) e^{−j2πft}

これに Mel Filter Bank $H_m(f)$

H_m(f) = \begin{cases} 0, & f < f(m-1) \\ \frac{f - f(m-1)}{f(m) - f(m-1)}, & f(m-1) \leq f < f(m) \\ 1, & f = f(m) \\ \frac{f(m+1) - f}{f(m+1) - f(m)}, & f(m) < f \leq f(m+1) \\ 0, & f > f(m+1) \end{cases}

をかけて積分したものが Mel Spectrogram。

S_m = \int df H_m(f) |X(f)|^2

Log-Mel Spectrogram はこれの Log をとったもの。

\text{Log-Mel}_m = \log(S_m)

$w(t)$ は Window Function。

$H_m(f)$ の中の $f(m)$ は Mel Scale の逆変換

f(m) = 700 ( 10^{m/2595} −1 )

$f = f(m)$ を中心に非対称な三角形の関数形をしている。

フーリエ変換は離散の場合はFFTで計算する。

mochineko

次は Meta の DINOv2 が Transformer ベースの CV モデルなので見てみたい。

https://dinov2.metademolab.com/

と思ったが画像データの入力方法以外は通常通りの Transformer なので詳しく見なくてもいいかも。

mochineko

長くなりそうな Stable Diffusion の実装を追ってみる。

Stable Diffusion 自体の解説は下記を参照する。

main.rs の fn run(...) を見てみると、基本的な流れは下記。

Prompt を text_embeddings に突っ込んで Embeddings に変換する
t2i ならランダムに、i2i なら元画像をベースに latents（VAE の低次元な潜在空間の Tensor）を生成する
各ステップで Sampling を実行して latents を更新していく
最終的な latents から VAE Decode で画像を生成する

Sampling のところで U-Net や Cross Attension など出てくるはずだがまだ具体的な処理をちゃんと理解できていない。

mochineko

とりあえず Text Encoder、Prompt のテキストを Embedding に変換する処理を追う。

基本的な流れは下記。

テキストを Tokenizer でトークン配列に変換
トークン配列を CLIP に通して Embeddings に変換
prompt と uncond_prompt それぞれの結果を結合

uncond_prompt は Unconditional Prompt だと思うが通常の Prompt とどう違うのか不明。

CLIP は Transformer ベースの Text Embegging モデルだが、LLaMA などと違って画像とペアで利用することを想定して設計されているという理解。

mochineko

ちょっと順番が前後してしまうが、Semantic Search の理解が怪しいことを自覚したので BERT の理解を先に進めたい。

とりあえずモデルの構成を見てみる。

pub struct BertModel {
    embeddings: BertEmbeddings,
    encoder: BertEncoder,
    pub device: Device,
    span: tracing::Span,
}

BertEmbeddings は文字通りテキストを Embeddings に変換する Layer。

BertEncoder は Embeddings を入力して Transformer に通して Embeddings を出力する Layer。

Transformer の構成は LLaMA で見たものとそう変わらなさそうなのでスキップ。

BertEmbeddings の構成は下記。

struct BertEmbeddings {
    word_embeddings: Embedding,
    position_embeddings: Option<Embedding>,
    token_type_embeddings: Embedding,
    layer_norm: LayerNorm,
    dropout: Dropout,
    span: tracing::Span,
}

word_embeddings はトークンを Embedding に変換する Layer、position_embeddings は Positional Encoding、token_type_embeddings は通常のテキストのトークンとは別に [CLS]（Classification Embedding、先頭に挿入する）、[SEP]（Separation Embegging？文章の切れ目に挿入する）という特別なトークンを Embedding に変換する Layer。

文章全体の比較をしたい場合には [CLS] トークンに対応する Embedding を使用するらしい。

ただ文章全体の比較のためだけに BERT を使うのは効率も精度も悪いので、専用に改良されたのが Sentence BERT というモデルという理解。

Semantic Search をする場合は文章全体の比較をしたいので、BERT ではなく Sentence BERT を使うと良いという理解。

Sentence BERT の改良点は [CLS] トークンではなく Pooling Layer を追加していること。

candle のサンプルだと avr-pooling、つまり平均のベクトルを文章全体のベクトルとして利用している。

mochineko

Stable Diffusion に戻って、VAE（Variational AutoEncoder）の確認をする。

参考は下記。

VAE では確率分布のパラメータを学習して確率的に潜在変数にエンコード、デコードできる。

画像そのものを Diffusion Model で生成しようとすると高解像度時の計算量が大きくなってしまうので、より低次元の潜在空間に落とす目的。

VAE の詳細はベイズ統計とかをちゃんとやってないと分からなさそう。（やってないので分からない）

candle / Stable Diffusion での実装は下記。

推論時に使う Decoder を見てみる。

struct Decoder {
    conv_in: nn::Conv2d,
    up_blocks: Vec<UpDecoderBlock2D>,
    mid_block: UNetMidBlock2D,
    conv_norm_out: nn::GroupNorm,
    conv_out: nn::Conv2d,
    #[allow(dead_code)]
    config: DecoderConfig,
}

impl Decoder {
    fn forward(&self, xs: &Tensor) -> Result<Tensor> {
        let mut xs = self.mid_block.forward(&self.conv_in.forward(xs)?, None)?;
        for up_block in self.up_blocks.iter() {
            xs = up_block.forward(&xs)?
        }
        let xs = self.conv_norm_out.forward(&xs)?;
        let xs = nn::ops::silu(&xs)?;
        self.conv_out.forward(&xs)
    }
}

順番的には下記。

conv_in （CNN）
mid_block （U-Net）
up_blocks （Resnet + Umsampling）
conv_norm_out （正規化）
nn::ops::silu （SiLU 活性化）
conv_out （CNN）

UNetMidBlock2D は下記。

pub struct UNetMidBlock2D {
    resnet: ResnetBlock2D,
    attn_resnets: Vec<(AttentionBlock, ResnetBlock2D)>,
    span: tracing::Span,
    pub config: UNetMidBlock2DConfig,
}

Resnet は Residual Network、LLaMA にも出てきた Residual Connection をするネットワーク構造。

実装は下記だが、CNN と Residual Connection の組み合わせになっているのが分かる。

問題なのは attn_renets で、AttentionBlock が入っているのが気になる。

Attention + Resnet は Transformer の Attention + MLP に似ている気がするが、VAE でも Attention を使うのはなぜなのか理解できていない。

→ VQ-VAE2 という VAE の改良版が内部で Attention を使用しているのでその流れかも。

また、VQ-VAE2ではPixelCNNにself-attentionの仕組みを取り入れたPixelSnailを参考にself-attentionの仕組みを導入します。
Topレベルの潜在変数は32×32のサイズでattentionを使ったPixelCNNを使って学習し、self-attentionを使います。
一方で、局所的な情報のみを含んでいるBottomレベルの方は、attentionを使うメリットが小さいことと、64×64とサイズが大きいのでメモリ負荷が大きいため、self-attentionは使いません。

つまり大局的な特徴を抽出するために Attention を取り入れているという理解。

もう一つ、UpDecoderBlock2D の構造も見ておく。

pub struct UpDecoderBlock2D {
    resnets: Vec<ResnetBlock2D>,
    upsampler: Option<Upsample2D>,
    span: tracing::Span,
    pub config: UpDecoderBlock2DConfig,
}

forward の実装を見ると、複数の Resnet に通した最後に Upsampling をかけているよう。

impl Module for UpDecoderBlock2D {
    fn forward(&self, xs: &Tensor) -> Result<Tensor> {
        let _enter = self.span.enter();
        let mut xs = xs.clone();
        for resnet in self.resnets.iter() {
            xs = resnet.forward(&xs, None)?
        }
        match &self.upsampler {
            Some(upsampler) => upsampler.forward(&xs, None),
            None => Ok(xs),
        }
    }
}

U-Net の Decode 部分に近い雰囲気？

総じて VAE なのに確率的な要素が見えないのはなぜ？

mochineko

U-Net とは何かも確認しておく。

オリジナルの U-Net の解説は下記。

CNN のモデルで、入出力が画像データ、U の下の部分でボトルネックになっていて、エンコード時のデータをデコード時に利用するのが特徴。

エンコード部分は次元を落とすので Pooling Layer があるが、デコード部分では逆に次元を上げるので Upsampling Layer が入っている。

Stable Diffusion では U-Net の構造を模した Resnet で構成されるブロックと Attention で構成されるブロックの構造が使われている。

candle / Stable Diffusion での実装は下記。

pub struct UNet2DConditionModel {
    conv_in: Conv2d,
    time_proj: Timesteps,
    time_embedding: TimestepEmbedding,
    down_blocks: Vec<UNetDownBlock>,
    mid_block: UNetMidBlock2DCrossAttn,
    up_blocks: Vec<UNetUpBlock>,
    conv_norm_out: nn::GroupNorm,
    conv_out: Conv2d,
    span: tracing::Span,
    config: UNet2DConditionModelConfig,
}

VAE の Decoder と似た雰囲気を感じるが、時刻の Embedding が入っていたり、UpBlock だけじゃなく DownBlock も入っている。（U-Net なので当たり前）

各 Block の構成も見ておく。

UNetDownBlock の構成は下記。

pub(crate) enum UNetDownBlock {
    Basic(DownBlock2D),
    CrossAttn(CrossAttnDownBlock2D),
}

通常の DownBlock と Cross Attention の DownBlock の二種類ある？

通常のは下記で、Resnet と Downsampler（Pooling）の組み合わせ。

pub struct DownBlock2D {
    resnets: Vec<ResnetBlock2D>,
    downsampler: Option<Downsample2D>,
    span: tracing::Span,
    pub config: DownBlock2DConfig,
}

Cross Attention 版は下記。

pub struct CrossAttnDownBlock2D {
    downblock: DownBlock2D,
    attentions: Vec<SpatialTransformer>,
    span: tracing::Span,
    pub config: CrossAttnDownBlock2DConfig,
}

SpatialTransformer は名前の通り空間的な Transformer で、Proj の in / out には Linear or CNN の　Layer が入る。

pub struct SpatialTransformer {
    norm: nn::GroupNorm,
    proj_in: Proj,
    transformer_blocks: Vec<BasicTransformerBlock>,
    proj_out: Proj,
    span: tracing::Span,
    pub config: SpatialTransformerConfig,
}

DownBlock の処理内で SpatialTransformer によって空間的な特徴を拾っている、という理解。

ところで Cross Attention は何との Cross をしているのかというと、encoder_hidden_states: Option<&Tensor>, らしい。

よーく辿ると

とあるので、Prompt のテキストの Embeddings が入ることになる。

つまり Prompt が効くのはこの Cross-Attention を取っている場合のみ。

追記: 中間層においては、常にSelf-Attention（あるふさんに教えていただきました。）

と参考記事にあるように、Down / Up Block では Cross-Attention で Prompt の Embeddings が取り入れられ、Middle Block では Self-Attention のみになるようので残りの Middle / Up も確認する。

mochineko

Middle Block の UNetMidBlock2DCrossAttn を見ていく。

pub struct UNetMidBlock2DCrossAttn {
    resnet: ResnetBlock2D,
    attn_resnets: Vec<(SpatialTransformer, ResnetBlock2D)>,
    span: tracing::Span,
    pub config: UNetMidBlock2DCrossAttnConfig,
}

CrossAttnDownBlock2D の DownBlock 部分が ResnetBlock に置き換わるだけ。

Up Block の UNetUpBlock も DownBlock 同様、Cross-Attention とそうでないもののバリエーションがある。

enum UNetUpBlock {
    Basic(UpBlock2D),
    CrossAttn(CrossAttnUpBlock2D),
}

CrossAttnUpBlock2D もほぼ Down の逆の構成で、Downsampler が Upsampler に置き換わるだけ。

pub struct CrossAttnUpBlock2D {
    pub upblock: UpBlock2D,
    pub attentions: Vec<SpatialTransformer>,
    span: tracing::Span,
    pub config: CrossAttnUpBlock2DConfig,
}

pub struct UpBlock2D {
    pub resnets: Vec<ResnetBlock2D>,
    upsampler: Option<Upsample2D>,
    span: tracing::Span,
    pub config: UpBlock2DConfig,
}

mochineko

一応時刻情報を埋め込んでいる処理も確認しておく。

Positional Encoding と同様に三角関数を使っているのが分かる。

mochineko

Stable Diffusion の U-Net のパーツの解像度は上がったので、全体の流れも確認しておく。

ソースコードのコメントのステップに従って追っていく。

座標系の調整（中心座標を調整する場合）
時刻情報を Embedding に変換
事前処理（CNN）
Down Block
Middle Block
Up Block
事後処理（Norm + SiLU + CNN）

オプションの down_block_additional_residuals mid_block_additional_residual でそれぞれの Residual に Offset を足せるようになっている。

下記の部分で DownBlock の Residual を UpBlock に反映しているのが分かる。（Residual Connection）

mochineko

main.rs に登場する scheduler の役割についても確認しておく。

DDIMScheduler とのことだが、DDIM といえば Sampling Method の一つ。

これが何をしているのか追ってみる。

pub struct DDIMScheduler {
    timesteps: Vec<usize>,
    alphas_cumprod: Vec<f64>,
    step_ratio: usize,
    init_noise_sigma: f64,
    pub config: DDIMSchedulerConfig,
}

主な関数な step と add_noise のよう。

とりあえず短い add_noise から。

impl DDIMScheduler {
    ...

    pub fn add_noise(&self, original: &Tensor, noise: Tensor, timestep: usize) -> Result<Tensor> {
        let timestep = if timestep >= self.alphas_cumprod.len() {
            timestep - 1
        } else {
            timestep
        };
        let sqrt_alpha_prod = self.alphas_cumprod[timestep].sqrt();
        let sqrt_one_minus_alpha_prod = (1.0 - self.alphas_cumprod[timestep]).sqrt();
        (original * sqrt_alpha_prod)? + (noise * sqrt_one_minus_alpha_prod)?
    }
}

時間 timestep に依存した係数を計算して、スケールさせながら元のデータ original にノイズを加えている。

要するに DIffusion Model の Forward Step の一般的な処理。

step の詳細も見ていく。

impl DDIMScheduler {
    ...

    /// Performs a backward step during inference.
    pub fn step(&self, model_output: &Tensor, timestep: usize, sample: &Tensor) -> Result<Tensor> {
        let timestep = if timestep >= self.alphas_cumprod.len() {
            timestep - 1
        } else {
            timestep
        };
        // https://github.com/huggingface/diffusers/blob/6e099e2c8ce4c4f5c7318e970a8c093dc5c7046e/src/diffusers/schedulers/scheduling_ddim.py#L195
        let prev_timestep = if timestep > self.step_ratio {
            timestep - self.step_ratio
        } else {
            0
        };

        let alpha_prod_t = self.alphas_cumprod[timestep];
        let alpha_prod_t_prev = self.alphas_cumprod[prev_timestep];
        let beta_prod_t = 1. - alpha_prod_t;
        let beta_prod_t_prev = 1. - alpha_prod_t_prev;

        let (pred_original_sample, pred_epsilon) = match self.config.prediction_type {
            PredictionType::Epsilon => {
                let pred_original_sample = ((sample - (model_output * beta_prod_t.sqrt())?)?
                    * (1. / alpha_prod_t.sqrt()))?;
                (pred_original_sample, model_output.clone())
            }
            PredictionType::VPrediction => {
                let pred_original_sample =
                    ((sample * alpha_prod_t.sqrt())? - (model_output * beta_prod_t.sqrt())?)?;
                let pred_epsilon =
                    ((model_output * alpha_prod_t.sqrt())? + (sample * beta_prod_t.sqrt())?)?;
                (pred_original_sample, pred_epsilon)
            }
            PredictionType::Sample => {
                let pred_original_sample = model_output.clone();
                let pred_epsilon = ((sample - &pred_original_sample * alpha_prod_t.sqrt())?
                    * (1. / beta_prod_t.sqrt()))?;
                (pred_original_sample, pred_epsilon)
            }
        };

        let variance = (beta_prod_t_prev / beta_prod_t) * (1. - alpha_prod_t / alpha_prod_t_prev);
        let std_dev_t = self.config.eta * variance.sqrt();

        let pred_sample_direction =
            (pred_epsilon * (1. - alpha_prod_t_prev - std_dev_t * std_dev_t).sqrt())?;
        let prev_sample =
            ((pred_original_sample * alpha_prod_t_prev.sqrt())? + pred_sample_direction)?;
        if self.config.eta > 0. {
            &prev_sample
                + Tensor::randn(
                    0f32,
                    std_dev_t as f32,
                    prev_sample.shape(),
                    prev_sample.device(),
                )?
        } else {
            Ok(prev_sample)
        }
    }
}

計算の内容はともかく、やっぱりマルコフ連鎖を理解してないせいで結局何をやっているのかが頭に入ってこない。

VAE のベイズ統計っぽい話もそうだが、やったことない数学の部分でつまづいているので軽くでも勉強しておいた方が良さそう。

mochineko

拡散モデルの基礎理論を解説している下記の書籍を読んだ。

物理の知識があるとすんなり読めた、後半の細かい数式は手を動かさないとまだ理解できていないが、基本的な仕組みや流れはおおよそ理解できた。

mochineko

基礎理論を理解したところで、改めて DDIM を見返してみる。

Scheduler というのはノイズスケジューラーで、拡散モデルの生成プロセスを管理しているところで、ノイズの加え方が方法論によって異なる。

DDIM（Denoising Diffusion Implicit Models）は DDPM（Denoising Diffusion Probabilistic Models）の改良版（正確には一般化）で、より少ないサンプリング数で高品質な生成ができるロジック。

DDIM の論文もせっかくなので読んでみる。

https://arxiv.org/pdf/2010.02502.pdf

DDIM の特徴は Non-Markovian な生成プロセスで、DDPM とは異なり (6) 式の確率の定義に $x_0$ が入っていて直前の状態だけでなく $x_0$ にも依存する点で、 $x_0$ は学習時の入力の画像に対応するもの。

DDPM で学習したモデルにそのまま DDIM を適用して生成を高速化できる。

実装の add_noise 関数は数式だと下記。

\bold{x}_{t} = \sqrt{ \bar{\alpha}_t } \bold{x}_0 + \sqrt{ \bar{\beta}_t } \bold{\epsilon} \\ \bar{ \alpha }_t = \prod_{s = 0}^{t} \alpha_s \\ \bar{\beta}_t = 1 - \bar{ \alpha }_t

これは入力 $\bold{x}_0$ に対してノイズを加える DDPM の拡散過程の定義そのもの。

step 関数の内容は数式だと下記。

\frac{ \sigma_t^2 }{ \eta } = \frac{ \bar{\beta}_{t-1} }{ \bar{\beta}_t } \left ( 1 - \frac{ \bar{\alpha}_{t-1} }{ \bar{\alpha}_t } \right ) \\ \bold{x}_{t-1} = \sqrt{ \bar{\alpha}_{t-1} } \bold{x}'_0 + \sqrt{ \bar{\beta}_{t-1} - \sigma_t^2 } \bold{e}_t + \sigma_t \bold{\epsilon}_t

$\eta$ はハイパーパラメータ、 $\bold{x}'_0$ は $\bold{x}_0$ の推論値、 $\bold{e}_t$ は $\bold{x}_t$ の方向、 $\bold{\epsilon}_t$ はガウシアンノイズ。

論文の (12) 式に対応していることが分かる。

これで DDIM の add_noise と step の意味が理解できた。

mochineko

DDIM まで理解できたところで、Stable Diffusion の全体の流れを再度確認する。

for idx in 0..num_samples { ... } は一度に複数画像を生成するループ。
let latents = match &init_latent_dist { ... } は latents の初期化。
for (timestep_index, &timestep) in timesteps.iter().enumerate() { ... } は Scheduler の timestep に沿って画像生成（Denoising）を行うループ。

生成ループ内の主な処理は下記。

3-1. let noise_pred = unet.forward(&latent_model_input, timestep as f64, &text_embeddings)?; で U-Net に通して加えるノイズを Prompt を考慮して推論する。

3-2. latents = scheduler.step(&noise_pred, timestep, &latents)?; でノイズの推論値と現在の latents を使用して Scheduler（DDIM）の生成ステップを実行し、latents を更新する。

3-3. if args.intermediary_images { ... } は途中経過の画像へのデコード処理（オプション）。

let image = vae.decode(&(&latents / 0.18215)?)?; で最終的な latents を VAE でデコードして画像を生成する。

当初より全体の流れ、処理の流れがはっきり理解できるようになった。