Zenn
📶

各種ソートアルゴリズムの比較

2023/11/11に公開
3件
Ruby
アルゴリズム
sort
tech

処理時間の比較

単位: ms

N=1000

アルゴリズム ランダム 昇順 降順 sin sin(2θ) 同値
バブルソート 140 0 194 159 148 0
選択ソート 67 66 68 67 67 67
挿入ソート 100 0 193 145 120 0
シェルソート 7 6 5 4 5 3
ヒープソート 5 5 5 5 5 1
マージソート 4 4 4 4 4 3
乱択クイックソート 3 2 3 3 3 56
ボゴソート TLE 0 TLE TLE TLE 0
スターリンソート WA 0 WA WA WA 0

N=5000

アルゴリズム ランダム 昇順 降順 sin sin(2θ) 同値
バブルソート 3464 1 4847 3987 3679 1
選択ソート 1667 1662 1681 1674 1666 1662
挿入ソート 2422 1 4859 3629 3040 1
シェルソート 47 23 34 29 33 24
ヒープソート 32 34 30 31 31 4
マージソート 25 25 22 24 23 21
乱択クイックソート 19 12 16 22 16 1351
ボゴソート TLE 1 TLE TLE TLE 1
スターリンソート WA 1 WA WA WA 1

共通の変数名やメソッドの意味

名前 意味
a ソート対象
set(i, v) a[i] = v
swap_at(i, j) a[i], a[j] = a[j], a[j]
compare(x, op, y) x.send(op, y)
compare_at(i, op, j) compare(a[i], op, a[j])

バブルソート

class BubbleSort < SortLogic::Base
  def perform
    (0...).each do |stop|
      swaped = false
      a.size.pred.downto(stop.next) do |i|
        if compare_at(i, :<, i.pred)
          swap_at(i, i.pred)
          swaped = true
        end
      end
      unless swaped
        break
      end
    end
  end
end


ﾊﾞﾌﾞﾙｿｰﾄ x ﾗﾝﾀﾞﾑ = 525 (比較: 4895, 交換: 2334, 書込: 0)

ﾊﾞﾌﾞﾙｿｰﾄ x 昇順 = 0 (比較: 99, 交換: 0, 書込: 0)

ﾊﾞﾌﾞﾙｿｰﾄ x 降順 = 742 (比較: 4950, 交換: 4950, 書込: 0)

ﾊﾞﾌﾞﾙｿｰﾄ x sin = 603 (比較: 4599, 交換: 3688, 書込: 0)

ﾊﾞﾌﾞﾙｿｰﾄ x sin(2θ) = 564 (比較: 4845, 交換: 3024, 書込: 0)

選択ソート

class SelectionSort < SortLogic::Base
  def perform
    a.each_index do |to|
      from = to
      (to.next...a.size).each do |i|
        if compare_at(i, :<, from)
          from = i
        end
      end
      swap_at(from, to)
    end
  end
end


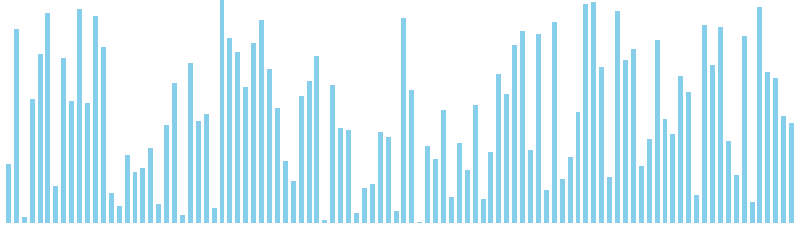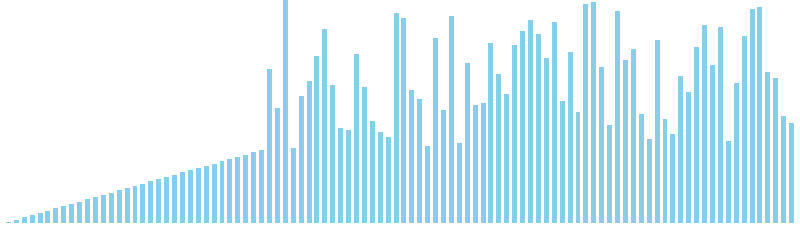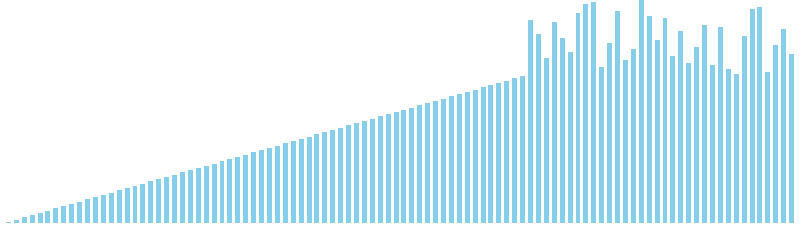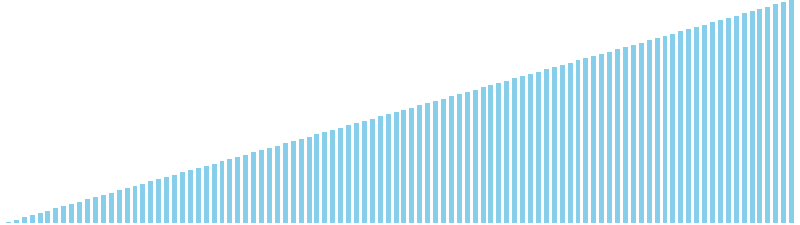
選択ｿｰﾄ x ﾗﾝﾀﾞﾑ = 256 (比較: 4950, 交換: 94, 書込: 0)

選択ｿｰﾄ x 昇順 = 254 (比較: 4950, 交換: 0, 書込: 0)

選択ｿｰﾄ x 降順 = 258 (比較: 4950, 交換: 50, 書込: 0)

選択ｿｰﾄ x sin = 258 (比較: 4950, 交換: 94, 書込: 0)

選択ｿｰﾄ x sin(2θ) = 258 (比較: 4950, 交換: 94, 書込: 0)

挿入ソート

class InsertionSort < SortLogic::Base
  def perform
    (1...a.size).each do |i|          # 左グループを徐々に大きくする
      i.downto(1) do |i|              # 左グループ内の右端から左端まで
        if compare_at(i.pred, :<=, i) # 左が自分以下なら (同値符号重要)
          break                       # おわる
        end
        swap_at(i.pred, i)            # パズドラ風に左に1つ移動する
      end
    end
  end
end


挿入ｿｰﾄ x ﾗﾝﾀﾞﾑ = 366 (比較: 2430, 交換: 2334, 書込: 0)

挿入ｿｰﾄ x 昇順 = 0 (比較: 99, 交換: 0, 書込: 0)

挿入ｿｰﾄ x 降順 = 740 (比較: 4950, 交換: 4950, 書込: 0)

挿入ｿｰﾄ x sin = 551 (比較: 3765, 交換: 3688, 書込: 0)

挿入ｿｰﾄ x sin(2θ) = 462 (比較: 3111, 交換: 3024, 書込: 0)

シェルソート

class ShellSort < SortLogic::Base
  def perform
    step = a.size / 2
    while step > 0
      (step...a.size).each do |i|
        v = a[i]
        j = i
        loop do
          if j < step
            break
          end
          k = j - step
          if compare(a[k], :<=, v)
            break
          end
          set j, a[k]
          j -= step
        end
        set j, v
      end
      step /= 2
    end
  end
end


ｼｪﾙｿｰﾄ x ﾗﾝﾀﾞﾑ = 13 (比較: 830, 交換: 0, 書込: 885)

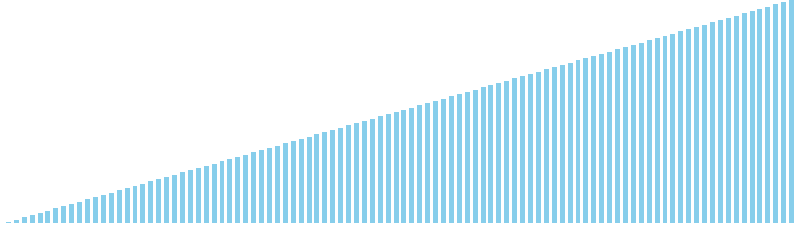
ｼｪﾙｿｰﾄ x 昇順 = 8 (比較: 503, 交換: 0, 書込: 503)

ｼｪﾙｿｰﾄ x 降順 = 11 (比較: 668, 交換: 0, 書込: 763)

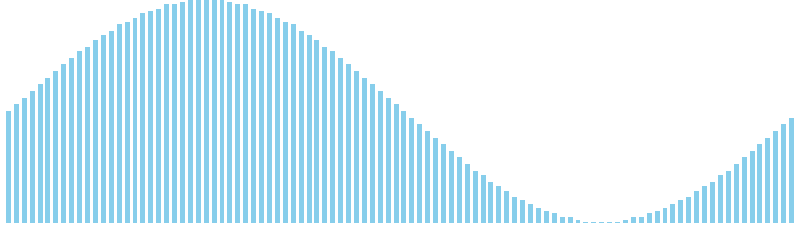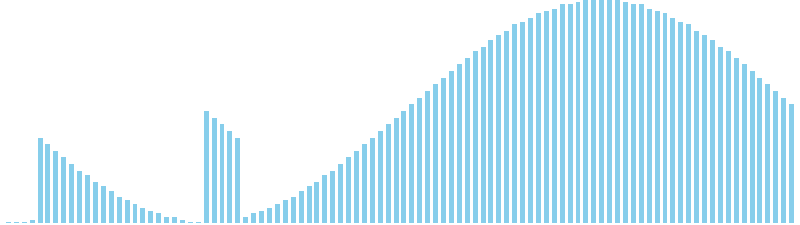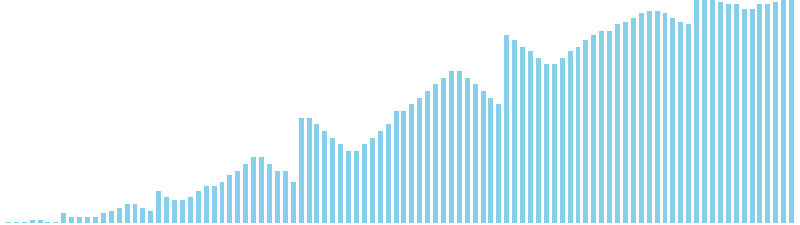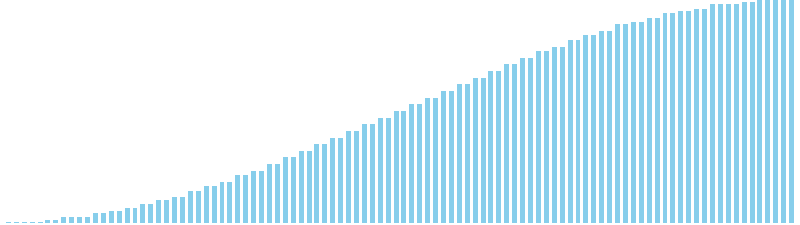
ｼｪﾙｿｰﾄ x sin = 9 (比較: 601, 交換: 0, 書込: 670)

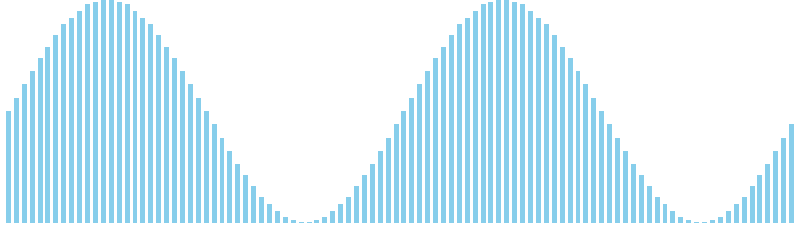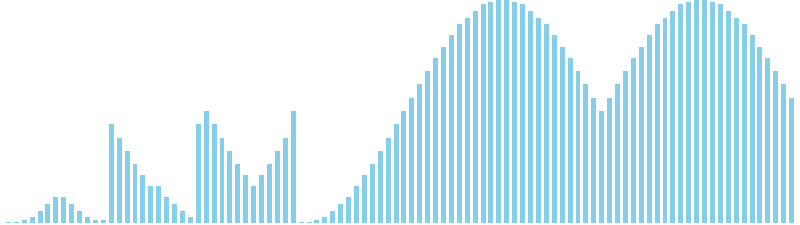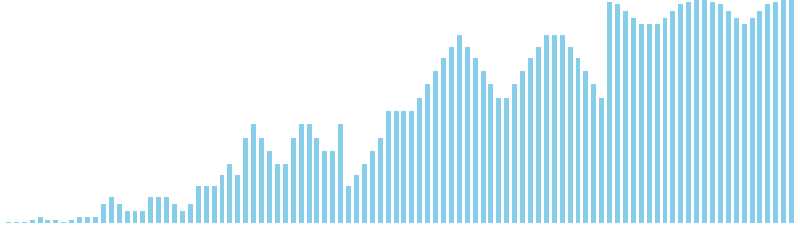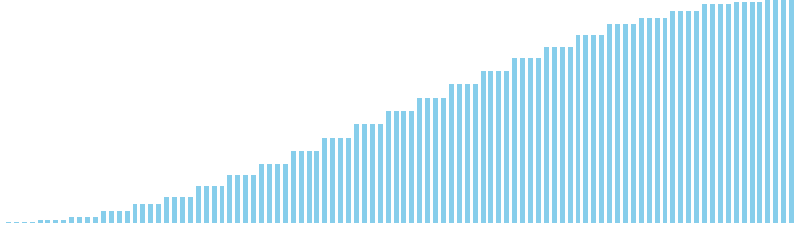
ｼｪﾙｿｰﾄ x sin(2θ) = 11 (比較: 702, 交換: 0, 書込: 739)

ヒープソート

class HeapSort < SortLogic::Base
  def perform
    # 配列を二分木と見なして最大値を頂上まで持っていく
    start = a.size / 2 - 1 # 「底辺から1つ上の層の右端の親」から開始する
    start.downto(0) do |i| # 左端まで行ったら1つ上の右端に移動を繰り返して頂上まで上がっていく
      heapify(a.size, i)   # n はずっと全体の個数
    end

    # 頂点から最大値を取り出していく
    #
    # このとき別の配列に入れていくのではなく木の右下(というか配列の最後)から前方に向って並べるように書き込んでいく
    # 書き込まれる位置にある値は頂点と入れ替えることで保持される
    # 頂点に移動した値は最大とは限らないのでまた整理する
    #
    # 木のサイズが減少していっているのは後ろに書き込んだ値たちの領域に触れないようにするため
    # (そうしないと最大値がまた頂上に上がってきてしまう)
    #
    # 最大値を書き込む後ろの位置はだんだん前にずれるので最終的な見た目は昇順になる
    (a.size - 1).downto(1) do |i|
      swap_at(i, 0)   # 右下と頂点を入れかえることで最大値が最後にくる
      heapify(i, 0)   # こっちの i はサイズを意味するので最大値のある場所(a[i])は保護される
    end
  end

  # 親・左子・右子の3人のなかでもっとも大きな値を持つのが誰か調べる
  # どちらかの子の方が大きな値を持っていれば親と子の値を入れ替える
  # 入れ替えた場合、その子を親と見なして同じことをする
  def heapify(size, parent)
    l = parent * 2 + 1 # parent から見た左子
    r = parent * 2 + 2 # parent から見た右子

    # △の角にいる3人のなかでもっとも大きな値を持つ人を i とする
    i = parent
    if l < size && compare_at(i, :<, l)
      i = l
    end
    if r < size && compare_at(i, :<, r)
      i = r
    end

    if i == parent
      # 親の方が大きな値を持っていたので OK
    else
      swap_at(parent, i) # 親の方が小さかったので下げる
      heapify(size, i)   # 下げられるところまでもっていく
    end
  end
end


ﾋｰﾌﾟｿｰﾄ x ﾗﾝﾀﾞﾑ = 11 (比較: 1026, 交換: 580, 書込: 0)

ﾋｰﾌﾟｿｰﾄ x 昇順 = 11 (比較: 1081, 交換: 640, 書込: 0)

ﾋｰﾌﾟｿｰﾄ x 降順 = 10 (比較: 944, 交換: 516, 書込: 0)

ﾋｰﾌﾟｿｰﾄ x sin = 10 (比較: 1001, 交換: 512, 書込: 0)

ﾋｰﾌﾟｿｰﾄ x sin(2θ) = 10 (比較: 988, 交換: 549, 書込: 0)

マージソート

class MergeSort < SortLogic::Base
  def perform
    merge_sort(0, a.size.pred)
  end

  def merge_sort(l, r)
    if l < r
      m = (l + r) / 2
      merge_sort(l, m)
      merge_sort(m.next, r)

      # 方法1
      # 要は l..r 間の値をソートしたい
      if false
        a[l..r] = a[l..r].sort
        return
      end

      # 以降は自力でソートする手順

      lhv = a[l..m]
      rhv = a[m.next..r]
      i = l

      # 方法2
      # 素直に並び換える
      if false
        # 両方を比べて小さい方から並べていく
        until lhv.empty? || rhv.empty?
          set i, (compare(lhv.first, :<, rhv.first) ? lhv : rhv).shift
          i += 1
        end

        # 左側だけ残っていれば追加する
        until lhv.empty? do
          set i, lhv.shift
          i += 1
        end

        # 右側だけ残っていれば追加する
        until rhv.empty? do
          set i, rhv.shift
          i += 1
        end
        return
      end

      # 方法3. 方法2の改良版
      # 「左側」と「反転した右側」を連結すると簡潔な処理になる
      # https://qiita.com/drken/items/44c60118ab3703f7727f#5-%E3%83%9E%E3%83%BC%E3%82%B8%E3%82%BD%E3%83%BC%E3%83%88-on-log-n
      if true
        ary = lhv + rhv.reverse
        until ary.empty?
          set i, compare(ary.first, :<, ary.last) ? ary.shift : ary.pop
          i += 1
        end
        return
      end
    end
  end
end


ﾏｰｼﾞｿｰﾄ x ﾗﾝﾀﾞﾑ = 8 (比較: 672, 交換: 0, 書込: 672)

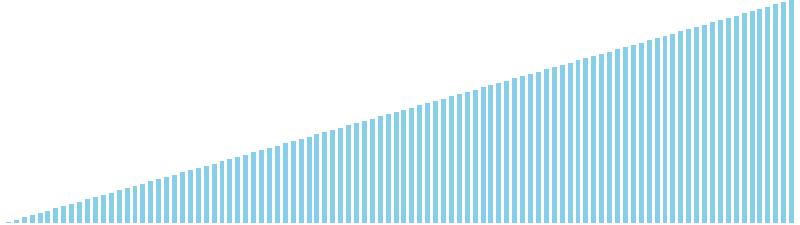
ﾏｰｼﾞｿｰﾄ x 昇順 = 8 (比較: 672, 交換: 0, 書込: 672)

ﾏｰｼﾞｿｰﾄ x 降順 = 8 (比較: 672, 交換: 0, 書込: 672)

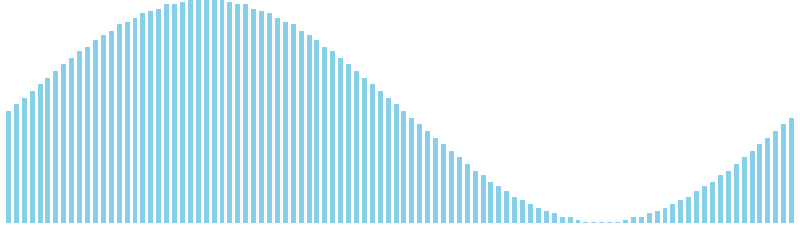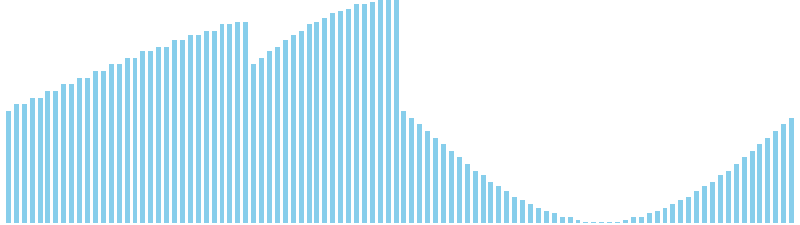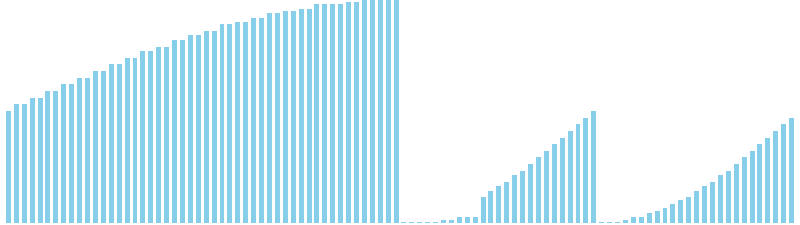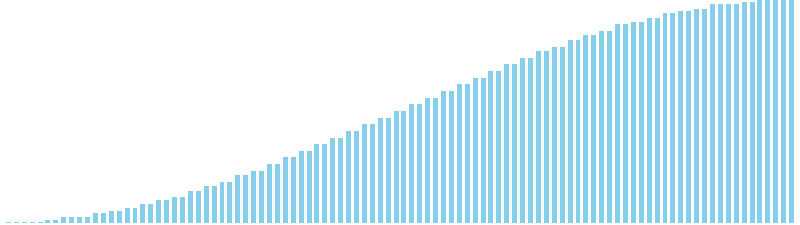
ﾏｰｼﾞｿｰﾄ x sin = 8 (比較: 672, 交換: 0, 書込: 672)

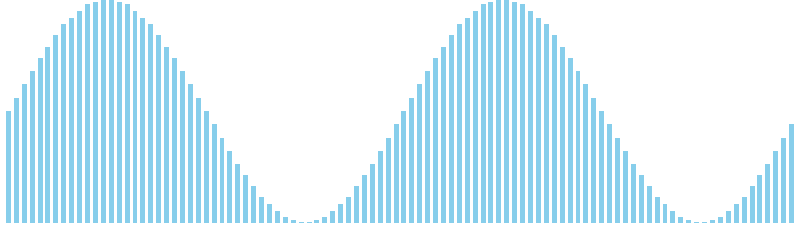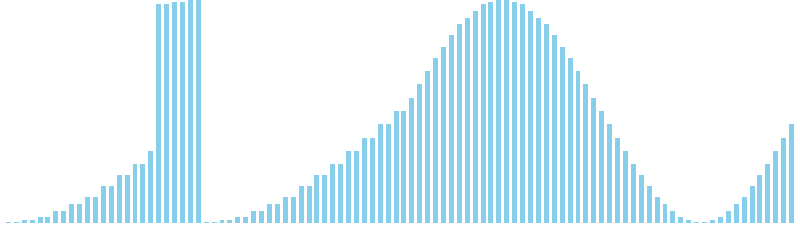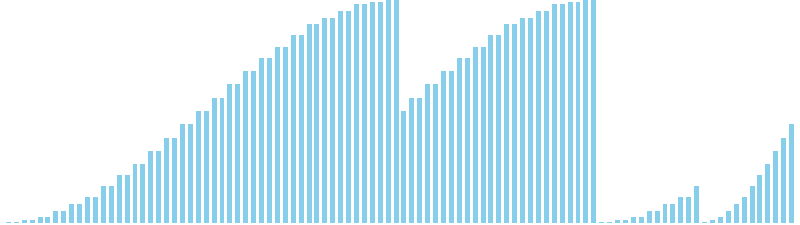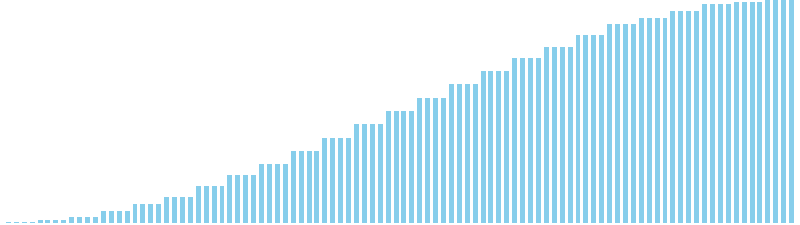
ﾏｰｼﾞｿｰﾄ x sin(2θ) = 8 (比較: 672, 交換: 0, 書込: 672)

乱択クイックソート

class RandQuickSort < SortLogic::Base
  def perform
    sort
  end

  def sort(l = 0, r = a.size.pred)
    if r <= l
      return
    end
    pi = rand(l..r)
    pivot = a[pi]
    swap_at(pi, r)
    i = l
    (l..r.pred).each do |j|
      if compare(a[j], :<, pivot)
        swap_at(i, j)
        i += 1
      end
    end
    swap_at(i, r)
    sort(l, i.pred)
    sort(i.next, r)
  end
end


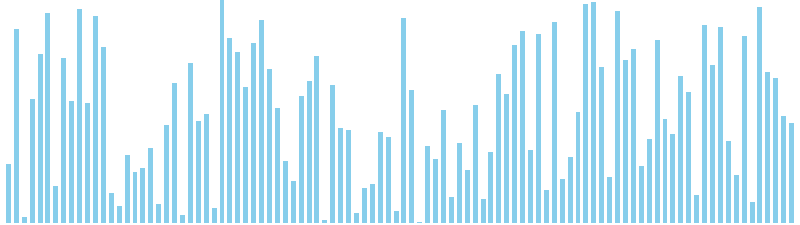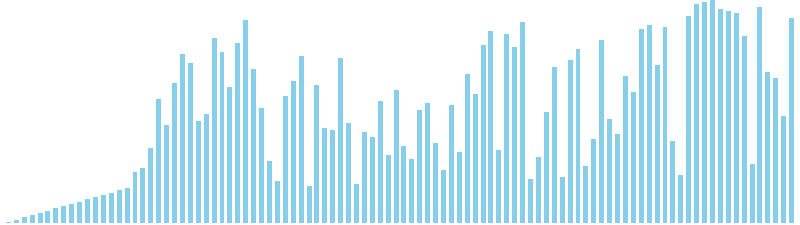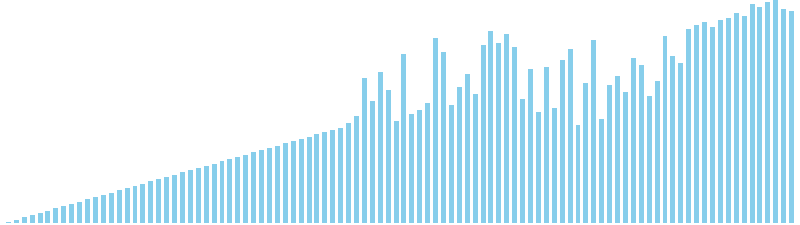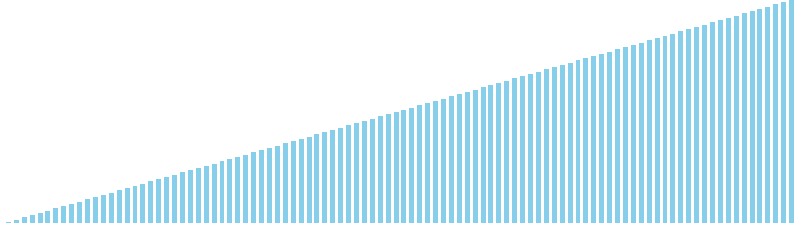
乱択ｸｲｯｸｿｰﾄ x ﾗﾝﾀﾞﾑ = 6 (比較: 838, 交換: 322, 書込: 0)

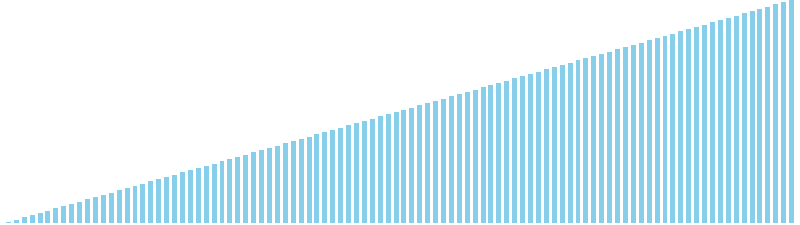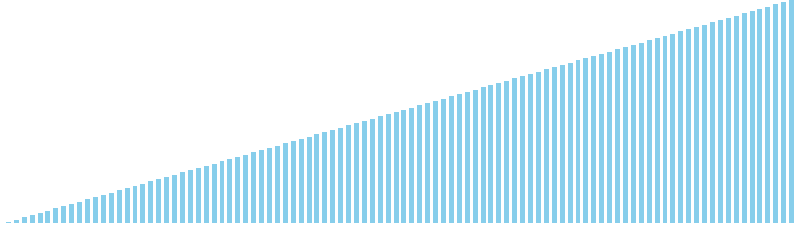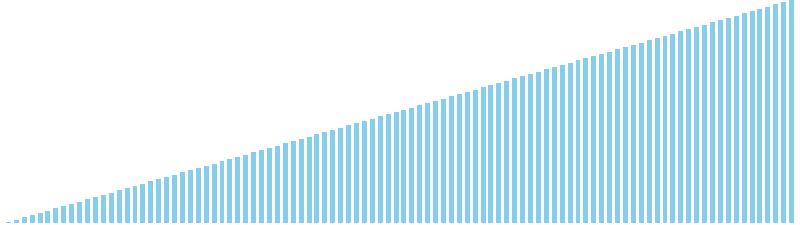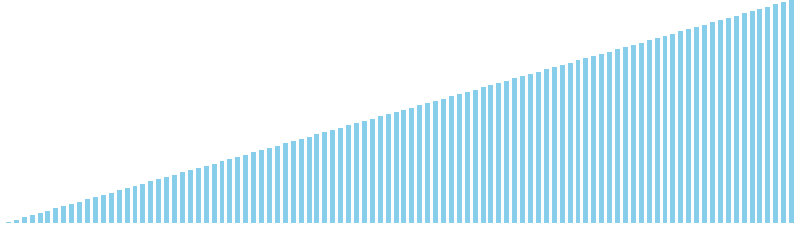
乱択ｸｲｯｸｿｰﾄ x 昇順 = 4 (比較: 624, 交換: 96, 書込: 0)

乱択ｸｲｯｸｿｰﾄ x 降順 = 5 (比較: 605, 交換: 280, 書込: 0)

乱択ｸｲｯｸｿｰﾄ x sin = 6 (比較: 613, 交換: 301, 書込: 0)

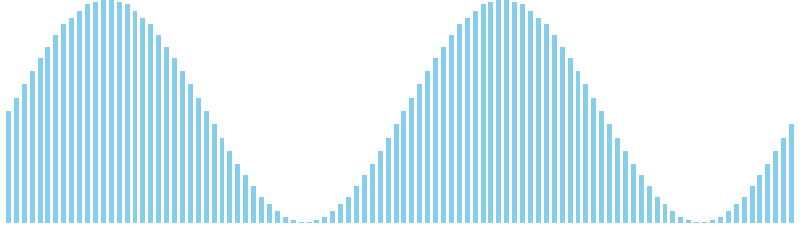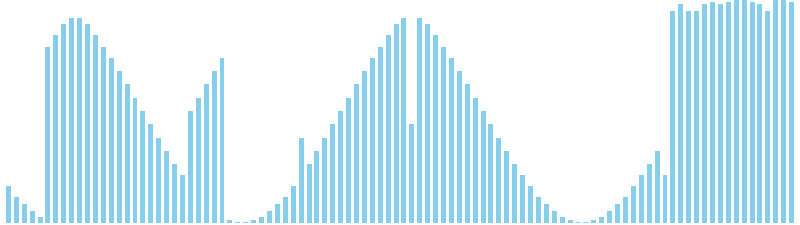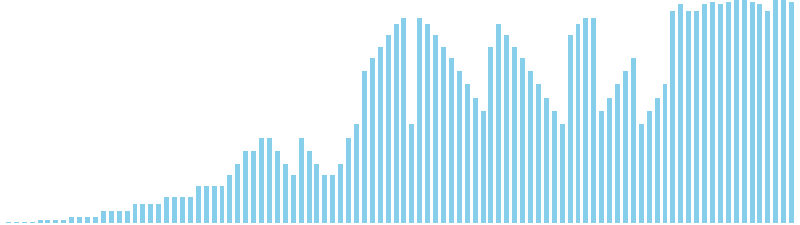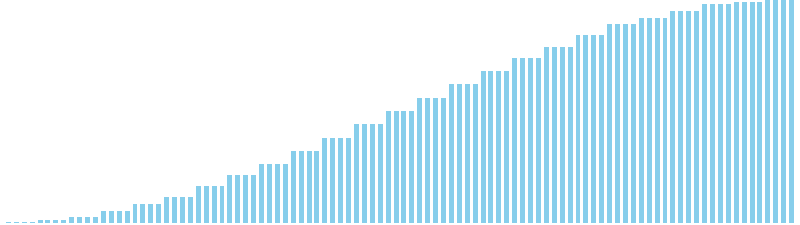
乱択ｸｲｯｸｿｰﾄ x sin(2θ) = 7 (比較: 642, 交換: 340, 書込: 0)

ボゴソート

class BogoSort < SortLogic::Base
  def perform
    until a.each_cons(2).all? { |a, b| compare(a, :<=, b) }
      a.size.pred.downto(1) { |i| swap_at(i, rand(i.next)) }
    end
  end
end


ﾎﾞｺﾞｿｰﾄ x ﾗﾝﾀﾞﾑ = TLE (比較: ∞, 交換: ∞, 書込: ∞)

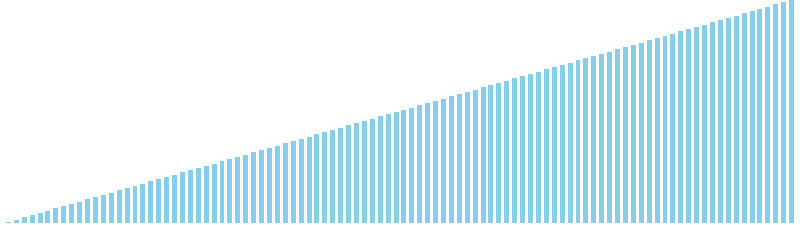
ﾎﾞｺﾞｿｰﾄ x 昇順 = 0 (比較: 99, 交換: 0, 書込: 0)

ﾎﾞｺﾞｿｰﾄ x 降順 = TLE (比較: ∞, 交換: ∞, 書込: ∞)

ﾎﾞｺﾞｿｰﾄ x sin = TLE (比較: ∞, 交換: ∞, 書込: ∞)

ﾎﾞｺﾞｿｰﾄ x sin(2θ) = TLE (比較: ∞, 交換: ∞, 書込: ∞)

スターリンソート

class StalinSort < SortLogic::Base
  def perform
    j = 0
    (1...a.size).each do |i|
      if compare(a[i], :<, a[j])
        set(i, nil)
      else
        j = i
      end
    end
    a.compact!
  end
end

a = [1, 2, 1, 2, 3, 1, 3, 2, 4]  # => [1, 2, 1, 2, 3, 1, 3, 2, 4]
StalinSort.new(a).call           # => [1, 2, 2, 3, 3, 4]

関連

https://zenn.dev/megeton/articles/c28d4454aba1f6
https://zenn.dev/megeton/articles/715508383aacf1
https://zenn.dev/megeton/articles/177fbdcaecb8bf

Discussion