バケット系ソートアルゴリズムを学ぶ
特徴
| アルゴリズム | バケツ個数 | マイナス値 | 重複 |
|---|---|---|---|
| バケットソート | 最大値 + 1 | ||
| バケットソート改 | 値の幅 | ○ | |
| 計数ソート | 最大値 + 1 | ○ | |
| 鳩の巣ソート | 値の幅 | ○ | ○ |
| 基数ソート | log(最大値, 基数) + 1 | ○ | |
| 基数ソート改 | log(値の幅 - 1, 基数) + 1 | ○ | ○ |
| バケットソート亜種 | 値の幅 / バケツ1つのサイズ + 1 | ○ | ○ |
処理時間の比較
N = 5000 単位: ms
| アルゴリズム | ランダム | 昇順 | 降順 | sin | sin(2θ) | 同値 |
|---|---|---|---|---|---|---|
| バブルソート | 3338 | 1 | 4574 | 3784 | 3476 | 1 |
| 乱択クイックソート | 18 | 11 | 16 | 16 | 19 | 1334 |
| バケットソート | 1 | 1 | 1 | WA | WA | 0 |
| バケットソート改 | 1 | 1 | 3 | WA | WA | 0 |
| 計数ソート | 1 | 2 | 1 | 1 | 1 | 1 |
| 鳩の巣ソート | 2 | 1 | 1 | 1 | 1 | 1 |
| 10進基数ソート | 4 | 4 | 4 | 5 | 4 | 4 |
| 256進基数ソート | 2 | 2 | 2 | 2 | 2 | 2 |
| 10進基数ソート改 | 5 | 5 | 5 | 4 | 5 | 1 |
| バケットソート亜種 | 2 | 1 | 1 | 1 | 1 | 1 |
バケットソート
0以上の重複のない値に使える早業。
def sort(a)
buckets = []
a.each { |e| buckets[e] = e }
buckets.compact
end
a = [7, 5, 1, 9, 3] # => [7, 5, 1, 9, 3]
sort(a) # => [1, 3, 5, 7, 9]
値を添字と見なし、配列に倒して nil を抜けば一瞬で並び換えられている。
重複がある場合は、
a = [0, 0, 0, 0, 0] # => [0, 0, 0, 0, 0]
sort(a) # => [0]
減ってしまうが同じ値は一つでいいときには好都合でもある。
配列に反映する部分は each_with_object を使えば一行で書ける。
[5, 3, 1].each_with_object([]) { |e, m| m[e] = e } # => [nil, 1, nil, 3, nil, 5]
が、別に読みやすくはならないので使わない。
in-place には向いてないけどやるなら、
def sort(a)
buckets = []
a.each { |e| buckets[e] = e }
# 方法1. 単にこれでもいい
# a.replace(buckets.compact)
# 方法2. compact を使わない方法
i = 0
buckets.each do |bucket|
if bucket
a[i] = bucket
i += 1
end
end
end
a = [7, 5, 1, 9, 3] # => [7, 5, 1, 9, 3]
sort(a)
a # => [1, 3, 5, 7, 9]
となる。
重複がない場合にのみ使えるはずだが「in-place」かつ「すべてが同じ値」の場合、ソートが失敗したように見えないというどうでもいい性質に書いていて気づいた。
a = [0, 0, 0, 0, 0] # => [0, 0, 0, 0, 0]
sort(a)
a # => [0, 0, 0, 0, 0]
これは重複が消える挙動を期待しているとはまるので、より安全に行くなら buckets を展開する前に a.clear とする。
ところでマイナス値を含めてソートするにはどうしたらいいだろう?
a = [-7, 5, -1, -9, 3]
sort(a) rescue $! # => #<IndexError: index -7 too small for array; minimum: 0>
バケットソート改
マイナス値に対応したもの。
def sort(a)
min = a.min
buckets = []
a.each { |e| buckets[e - min] = e }
buckets.flatten.compact
end
a = [-7, 5, -1, -9, 3] # => [-7, 5, -1, -9, 3]
sort(a) # => [-9, -7, -1, 3, 5]
計数ソート (分布数えソート)
重複がある場合にも対応する。
def sort(a)
# 分布数を調べる
buckets = []
a.each do |value|
buckets[value] ||= 0
buckets[value] += 1
end
# 展開する
i = 0
buckets.each.with_index do |count, value|
if count
count.times do
a[i] = value
i += 1
end
end
end
a
end
a = [3, 1, 3, 1, 1] # => [3, 1, 3, 1, 1]
sort(a) # => [1, 1, 1, 3, 3]
入力が [3, 1, 3, 1, 1] のとき buckets は [nil, 3, nil, 2] になる。展開するときはインデックス 1 にある 3 は「1 が 3 つある」という意味なので最初は [1, 1, 1] になる。次のインデックス 3 にある 2 は「3 が 2 つある」なので続けて追加し [1, 1, 1, 3, 3] になる。
なぜ tally を使わない?
一見、分布に配列を使うのは悪手に見える。そこで仮にハッシュで返す tally を使うと、
a = [3, 1, 3, 1, 1]
buckets = a.tally # => {3=>2, 1=>3}
buckets.flat_map { |e, count| [e] * count } # => [3, 3, 1, 1, 1]
グループ化されてはいるものの並び替えに失敗する。したがって非効率に見える配列を使うことに意味がある。
ロジックを改善したつもりが遅くなった展開処理
こちらで紹介されているロジックを参考に書いたのが
これで、
def sort2(a)
# 数え上げる
buckets = Array.new(a.max.next, 0)
a.each { |value| buckets[value] += 1 }
# 累積和の形にする
(1...buckets.size).each do |i|
buckets[i] += buckets[i.pred]
end
# 展開する
# ここの部分は紙に書かないと理解不能
sorted = []
a.each do |value|
sorted[buckets[value].pred] = value
buckets[value] -= 1 # 同じ値を右から左に敷き詰めていくため
end
# 元を更新したことにする
a.replace(sorted)
end
a = [3, 1, 3, 1, 1]
sort2(a.dup) # => [1, 1, 1, 3, 3]
速度を比べてみると、
require "active_support/core_ext/benchmark"
a = 1000000.times.collect { rand(1000) }
Benchmark.ms { sort(a.dup) }.round(8) # => 123.43099999
Benchmark.ms { sort2(a.dup) }.round(8) # => 136.852
逆に遅くなった。これならシンプルな展開方法を使った方がよさそう。
鳩の巣ソート
計数ソートの改良版で値の範囲分だけバケツを確保する。
def sort(a)
min = a.min
# 分布数を調べる
buckets = []
a.each do |value|
i = value - min # 下駄を外す
buckets[i] ||= 0
buckets[i] += 1
end
# 展開する
i = 0
buckets.each.with_index do |count, value|
if count
count.times do
a[i] = min + value # 下駄を履く
i += 1
end
end
end
a
end
a = [100, 102, 101, 103] # => [100, 102, 101, 103]
sort(a) # => [100, 101, 102, 103]
計数ソートと鳩の巣ソートの違いがなかなかわからなかったが (ChatGPT が言うには) バケツのインデックス 0 に値の 0 の個数を入れるか、最低値の個数を入れるかの違いだけらしい。したがって上の例の場合、計数ソートであれば容量 104 の配列が確保されるが、鳩の巣の場合は容量 4 だけで済む。
鳩の巣ソートは本来、バケツ個数をケチる目的の改良だったかもしれないが、結果としてマイナス値も許容する。
a = [-100, -102, -101, -103] # => [-100, -102, -101, -103]
sort(a) # => [-103, -102, -101, -100]
そういう意味では「マイナス値対応計数ソート」とも言える。
バケツを事前に用意する
ここまでバケツの確保を
buckets = []
としたが最初からきっちり確保しておかないと気が済まない場合は
バケットソートや計数ソートの場合:
buckets = Array.new(a.max.next, 0)
鳩の巣ソートの場合:
min, max = a.minmax
buckets = Array.new((min..max).size, 0)
などとしておく。
自動拡張してくれる Ruby の Array の容量をわざわざ自分で管理したくないのでやらないけど、言語によってはあらかじめ確保しておかないといけない。
基数ソートの仕組み
巨大な配列が不要になる。
まず抽象化したコードで仕組みだけを理解する
a = [14, 22, 13, 21] # => [14, 22, 13, 21]
a = a.sort_by { |e| e.digits(10)[0] } # => [21, 22, 13, 14]
a = a.sort_by { |e| e.digits(10)[1] } # => [13, 14, 21, 22]
1桁目2桁目の順でソートすると終わっている。
桁が異なる場合に注意する
1桁しかない値の2桁目を参照すると nil になる
5.digits(10) # => [5]
5.digits(10)[1] # => nil
なので nil なら 0 を返すようにする。
a = [10, 5] # => [10, 5]
a = a.sort_by { |e| e.digits(10)[0] || 0 } # => [10, 5]
a = a.sort_by { |e| e.digits(10)[1] || 0 } # => [5, 10]
たまに順番がおかしい理由
a = [159, 106, 303, 495, 634, 902, 974, 910]
a = a.sort_by { |e| e.digits(10)[0] || 0 } # => [910, 902, 303, 634, 974, 495, 106, 159]
a = a.sort_by { |e| e.digits(10)[1] || 0 } # => [106, 902, 303, 910, 634, 159, 974, 495]
a = a.sort_by { |e| e.digits(10)[2] || 0 } # => [159, 106, 303, 495, 634, 910, 974, 902]
a == a.sort # => false
先頭に来るはずの 106 が 2 番目に来ているのがわかる。これは sort_by が安定ソートではないのが原因。
安定ソート版
a = [159, 106, 303, 495, 634, 902, 974, 910]
a = a.sort_by.with_index { |e, i| [e.digits(10)[0] || 0, i] } # => [910, 902, 303, 634, 974, 495, 106, 159]
a = a.sort_by.with_index { |e, i| [e.digits(10)[1] || 0, i] } # => [902, 303, 106, 910, 634, 159, 974, 495]
a = a.sort_by.with_index { |e, i| [e.digits(10)[2] || 0, i] } # => [106, 159, 303, 495, 634, 902, 910, 974]
a == a.sort # => true
sort_by で返す値にインデックスを含めると安定ソートになる。これでソート結果も正しくなった。
桁を動的に求めるには?
桁は
v = 12345678
Math.log(v, 10).floor.next # => 8
v.digits(10).size # => 8
v.to_s(10).size # => 8
などで求まる。
しかし log は 0 を与えると 1 にならないので桁を求める目的と噛み合っていない。
Math.log(0, 10) # => -Infinity
一方、負に対する digits は例外を出してしまう。
-1.digits rescue $! # => #<Math::DomainError: out of domain>
が、バケットソートは負の値に対応できないので例外が出るのはむしろありがたい。to_s はソートをするのに文字列化の処理が入るのが気持ち悪い。したがって digits がよさそう。
とりあえずソート対象の桁は
a = [159, 106, 303, 495, 634, 902, 974, 910]
n = a.max.digits(10).size # => 3
で求まるとして
n.times do |digit|
a = a.sort_by.with_index { |e, i| [e.digits(10)[digit] || 0, i] }
end
a # => [106, 159, 303, 495, 634, 902, 910, 974]
a == a.sort # => true
とすれば簡潔になる。
完成
def sort(a, radix: 10)
a.max.digits(radix).size.times do |digit|
a = a.sort_by.with_index do |e, i|
[e.digits(radix)[digit] || 0, i]
end
end
a
end
a = [159, 106, 303, 495, 634, 902, 974, 910]
sort(a) # => [106, 159, 303, 495, 634, 902, 910, 974]
次にバケットを使う方法に直す。
基数ソート (本物)
def sort(a, radix: 10)
# 最大の桁数を求める。10進数で 100 なら 3 を求める。
digits = a.max.digits(radix).size
# 桁数分のバケツ。最大値の影響を(ほぼ)受けない。
buckets = Array.new(radix) { [] }
digits.times do |i|
exp = radix**i # 10進であれば 1, 10, 100 と進む
# 現在の桁の数字 0-9 を添字にしてバケツに入れる
# 一つのバケツには何個も入る
a.each do |value|
digit = (value / exp) % radix
buckets[digit] << value
end
# すべてのバケツからそっと出して並べる
# 方法1-3 どの方法でもよい
# 方法1. 要するにこうしたい
if false
a.replace(buckets.flatten)
buckets.each(&:clear)
end
# 方法2. バケツごとに処理
if false
a.clear
buckets.each do |bucket|
a.concat(bucket)
bucket.clear
end
end
# 方法3. バケツ内の要素ごと
if true
i = 0
buckets.each do |bucket|
bucket.each do |value|
a[i] = value
i += 1
end
bucket.clear
end
end
end
a
end
a = [793, 12, 195, 241, 237, 448, 18, 124]
sort(a) # => [12, 18, 124, 195, 237, 241, 448, 793]
基数はなんでもいい。
2進数:
a = [793, 12, 195, 241, 237, 448, 18, 124]
sort(a, radix: 2) # => [12, 18, 124, 195, 237, 241, 448, 793]
123進数:
a = [793, 12, 195, 241, 237, 448, 18, 124]
sort(a, radix: 123) # => [12, 18, 124, 195, 237, 241, 448, 793]
radix**i が気になるなら
exp = 1
digits.times do
# ...
exp *= radix
end
としてもいい。
基数ソート改
鳩の巣ソートの要領で下駄を外せばマイナス値が扱える。
def sort(a, radix: 10)
min, max = a.minmax
digits = (max - min).digits(radix).size
buckets = Array.new(radix) { [] }
exp = 1
digits.times do
a.each do |value|
value -= min # 下駄を外す
digit = (value / exp) % radix
buckets[digit] << value
end
# 展開
i = 0
buckets.each do |bucket|
bucket.each do |value|
a[i] = min + value # 下駄を履く
i += 1
end
bucket.clear
end
exp *= radix
end
a
end
a = [-793, -12, -195, -241, -237, -448, -18, -124]
sort(a) # => [-793, -448, -241, -237, -195, -124, -18, -12]
バケットソート亜種
バケツ1つでカバーする範囲を増やしてバケツの個数を減らすように工夫したもの。ChatGPT に教わったいろんなパターンの一つだけど名称がわからないので「バケットソート亜種」としといた。
def sort(a, capacity: 10)
if a.empty?
return a
end
min, max = a.minmax # => [10000, 50000], [-3, 3]
bucket_count = ((min..max).size / capacity).next # => 5, 1
buckets = Array.new(bucket_count) { [] }
a.each do |value|
i = (value - min) / capacity
buckets[i] << value
end
buckets.each(&:sort!)
buckets.flatten
end
a = [50000, 20000, 10000, 20000, 40000]
sort(a, capacity: 10000) # => [10000, 20000, 20000, 40000, 50000]
最大値が 50000 なので計数ソートであればバケツを 50001 個用意しないといけない。一方、この方法であればバケツ1つでカバーする範囲を 10000 とすればバケツは5個で済む。またマイナス値も許容する。
a = [-1, 3, -2, 0, 2, -3, 1]
sort(a) # => [-3, -2, -1, 0, 1, 2, 3]
欠点は capacity 個毎にソートしないといけない部分で、分割されるので比較回数が減って高速に動作するとはいえ、比較しないことに全振りなバケットソートの特徴があまり活かされていないとも言える。
可視化
バケットソート
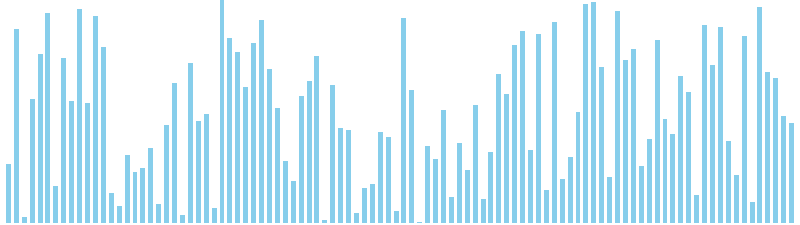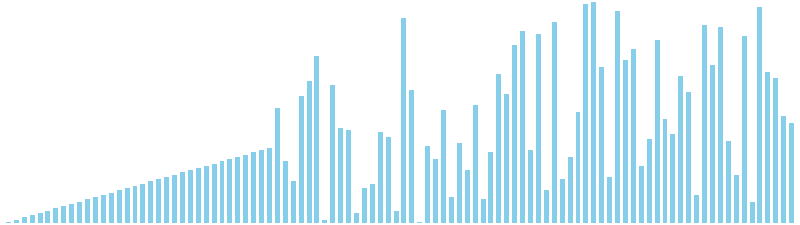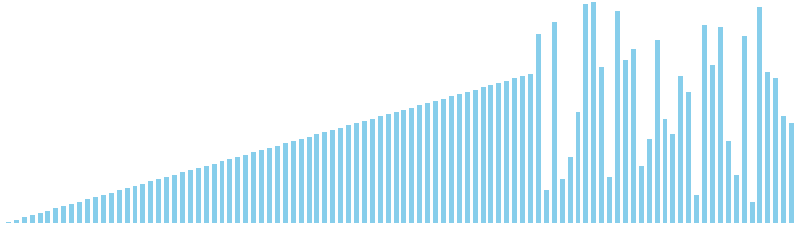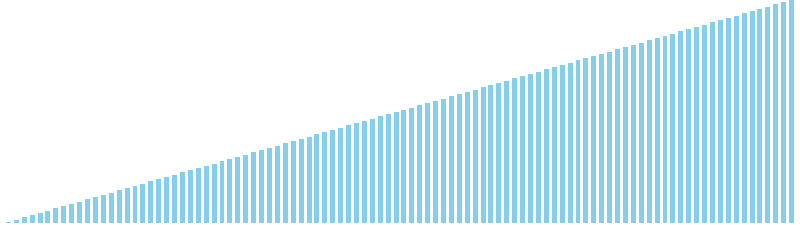
バケットソート x ランダム = 27 ns (比較: 0, 交換: 0, 書込: 100)
バケットソート x 昇順 = 23 ns (比較: 0, 交換: 0, 書込: 100)
バケットソート x 降順 = 26 ns (比較: 0, 交換: 0, 書込: 100)
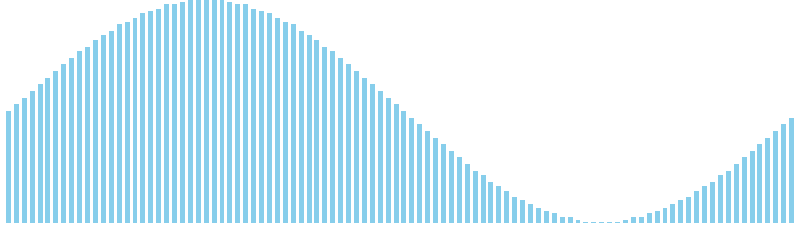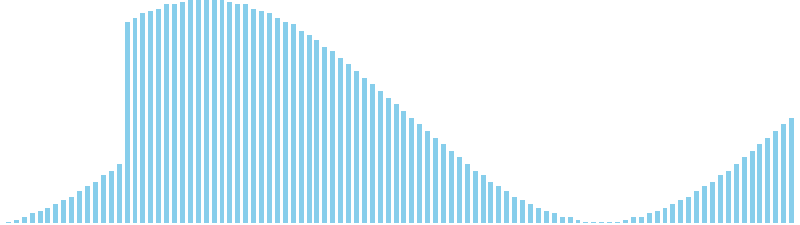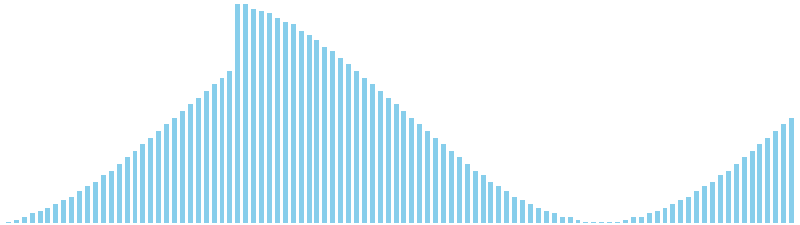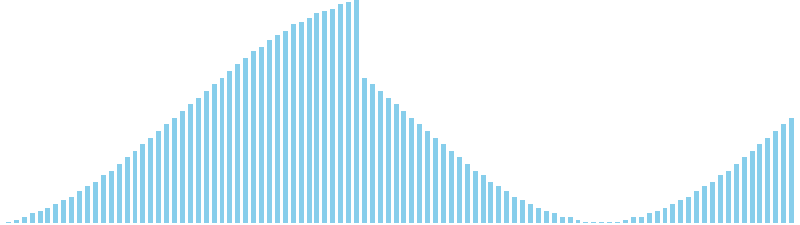
バケットソート x sin = WA (比較: 0, 交換: 0, 書込: 45)
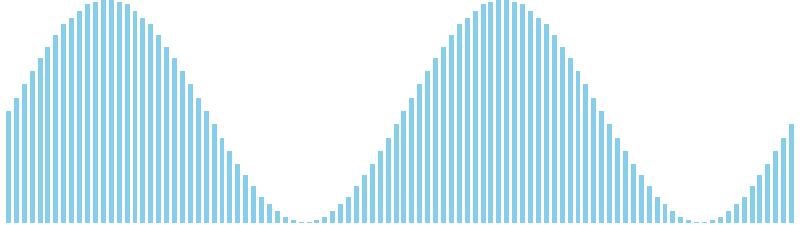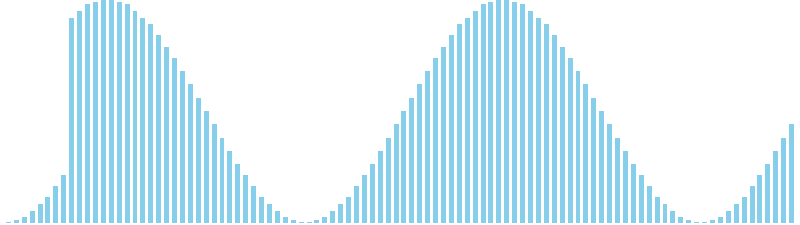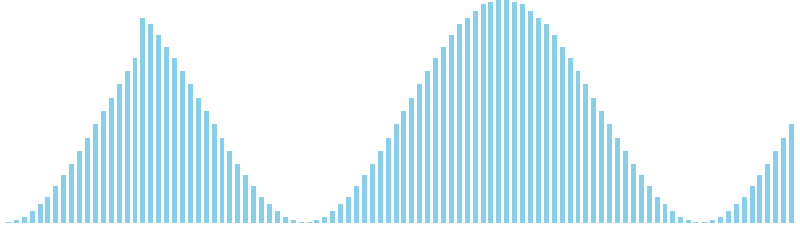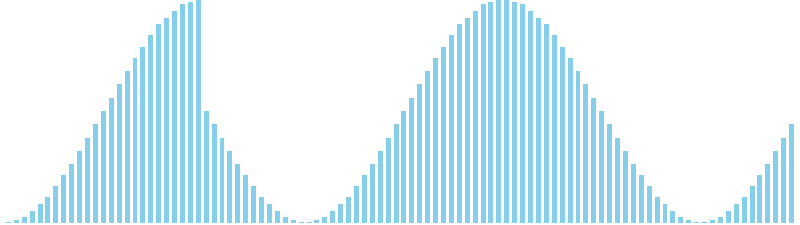
バケットソート x sin(2θ) = WA (比較: 0, 交換: 0, 書込: 25)
バケットソート改
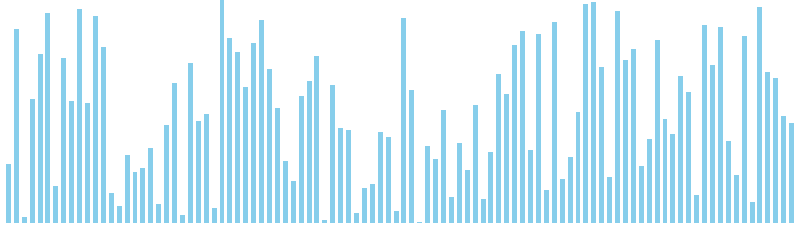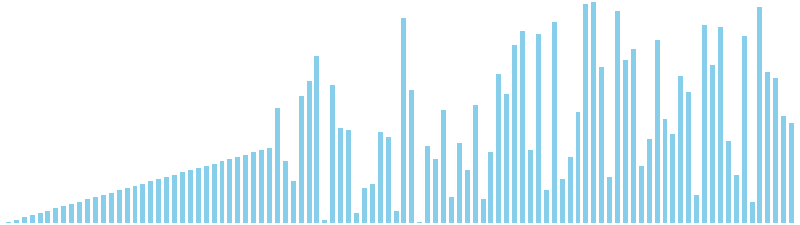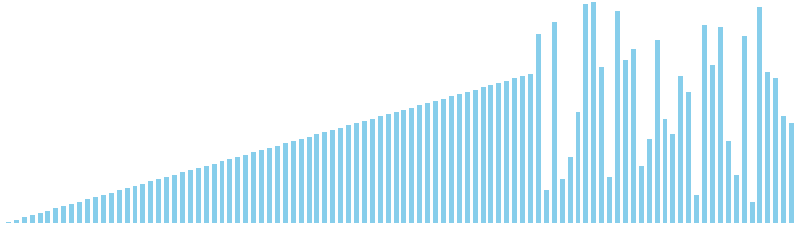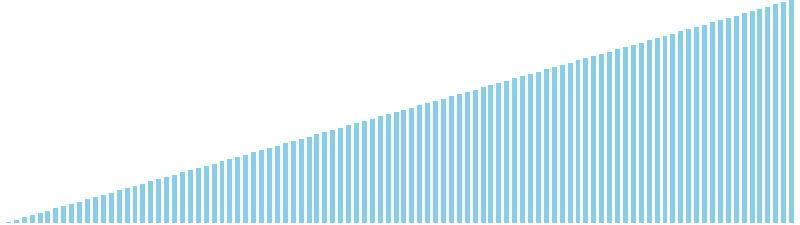
バケットソート改 x ランダム = 27 ns (比較: 0, 交換: 0, 書込: 100)

バケットソート改 x 昇順 = 29 ns (比較: 0, 交換: 0, 書込: 100)
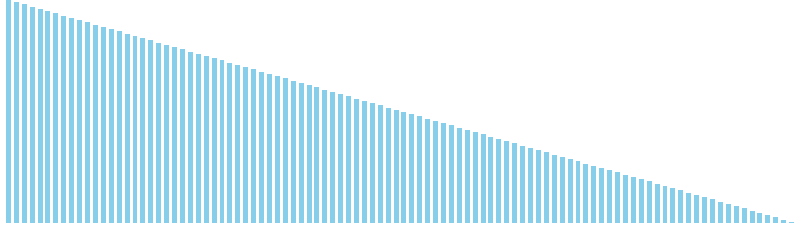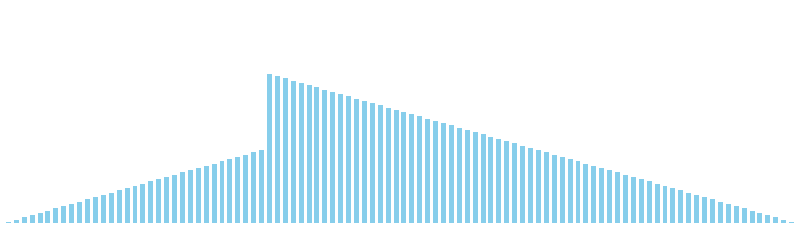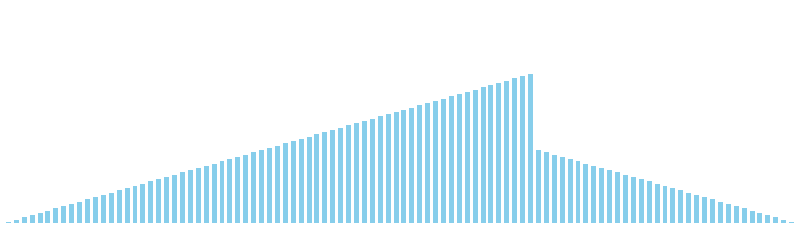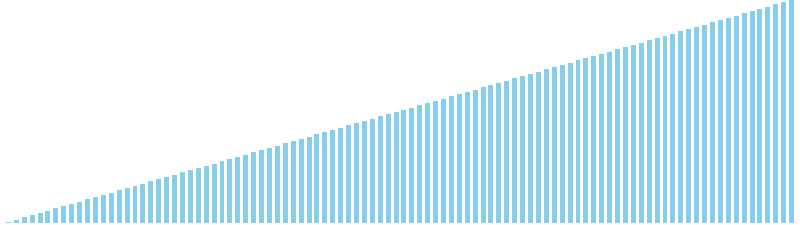
バケットソート改 x 降順 = 27 ns (比較: 0, 交換: 0, 書込: 100)
バケットソート改 x sin = WA (比較: 0, 交換: 0, 書込: 45)
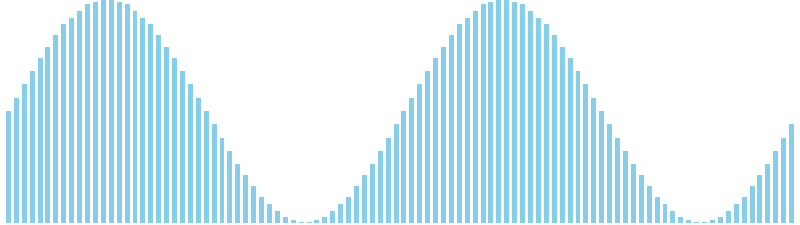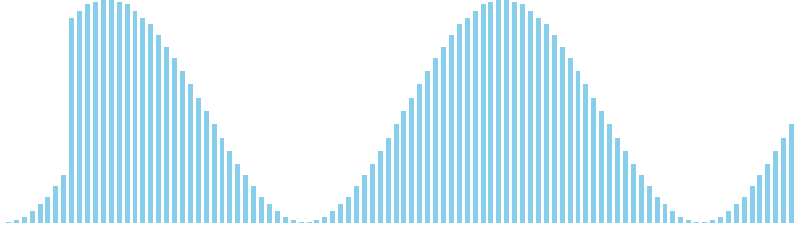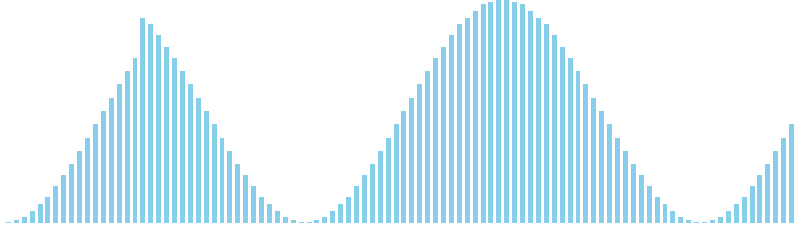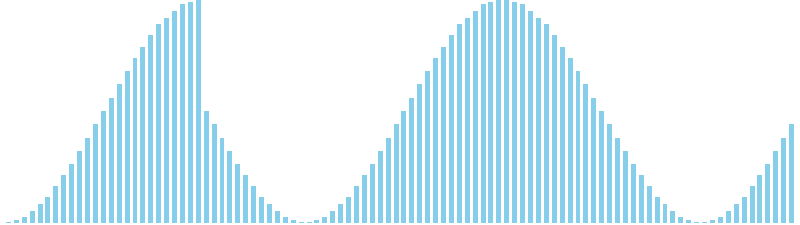
バケットソート改 x sin(2θ) = WA (比較: 0, 交換: 0, 書込: 25)
計数ソート
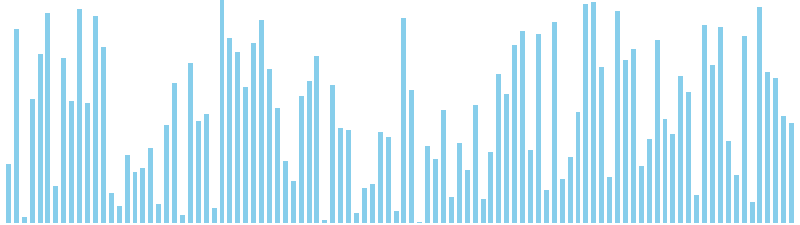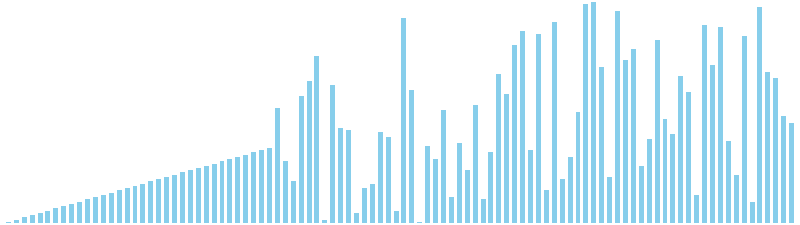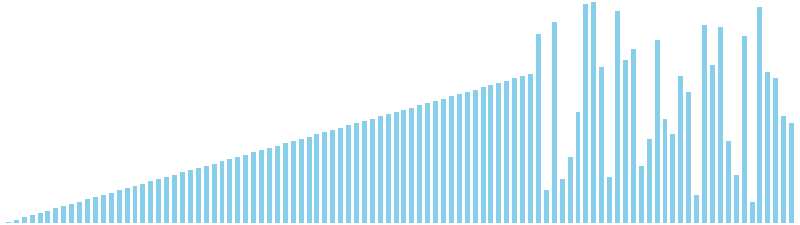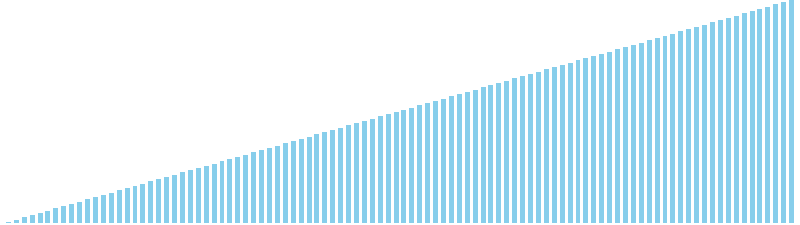
計数ソート x ランダム = 37 ns (比較: 0, 交換: 0, 書込: 100)
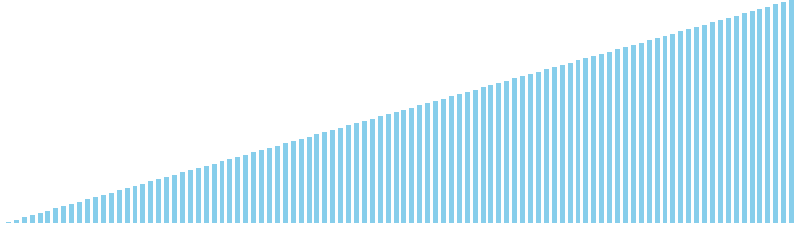
計数ソート x 昇順 = 39 ns (比較: 0, 交換: 0, 書込: 100)
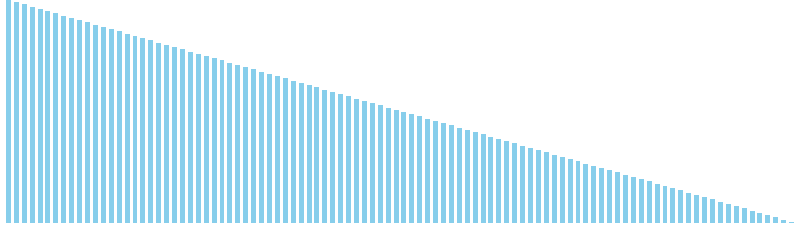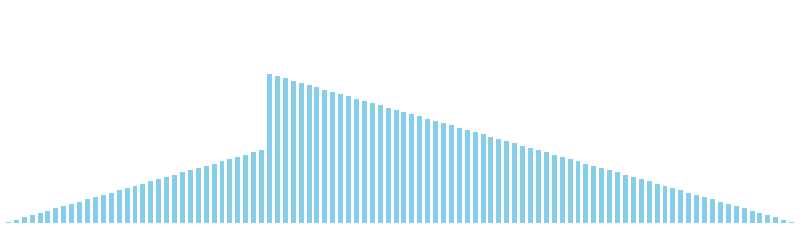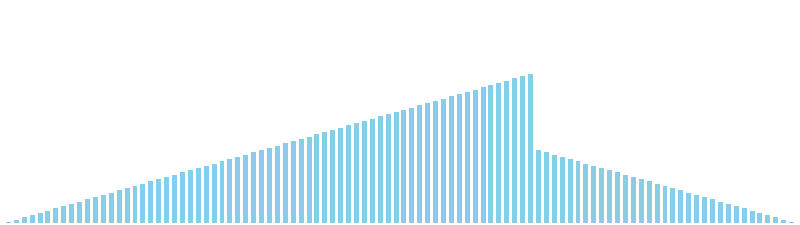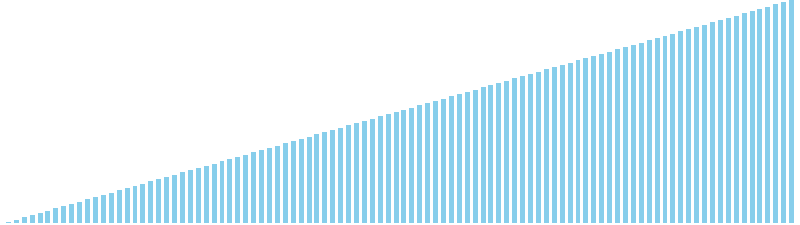
計数ソート x 降順 = 36 ns (比較: 0, 交換: 0, 書込: 100)
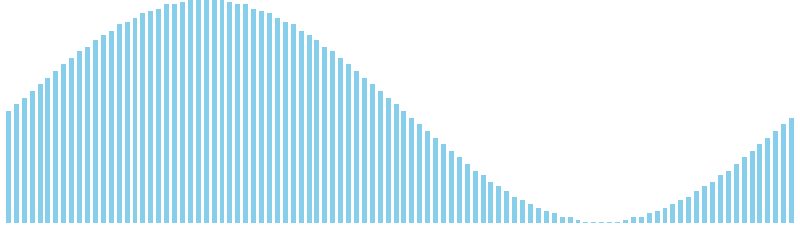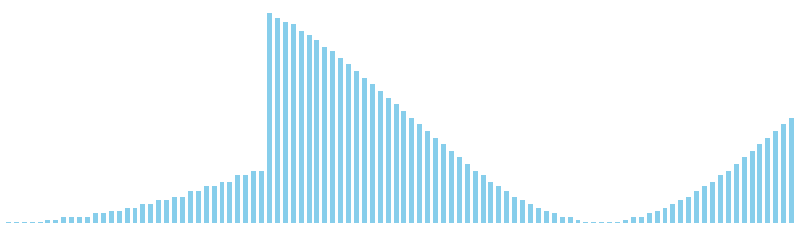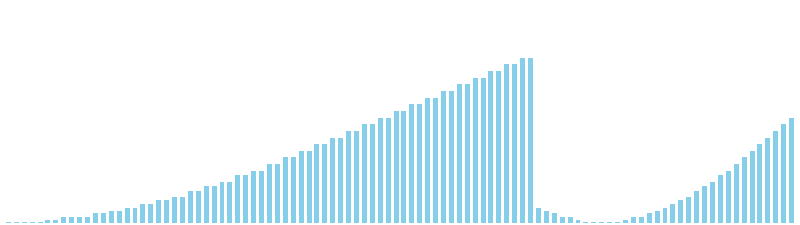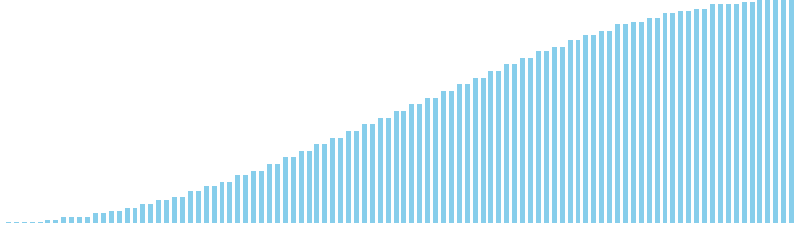
計数ソート x sin = 36 ns (比較: 0, 交換: 0, 書込: 100)
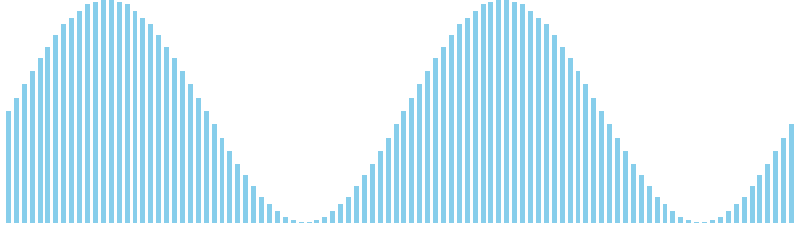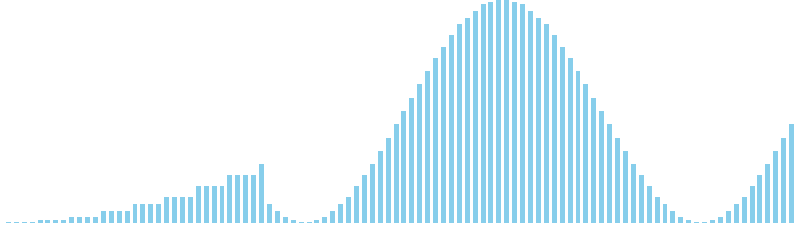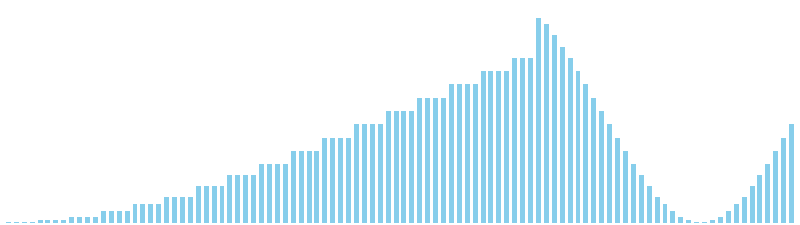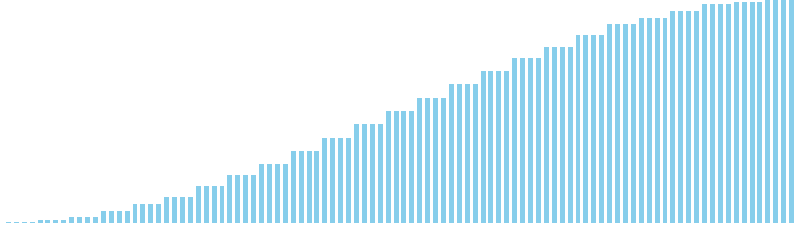
計数ソート x sin(2θ) = 35 ns (比較: 0, 交換: 0, 書込: 100)
鳩の巣ソート
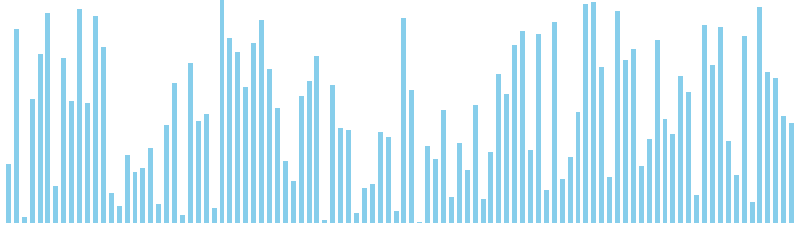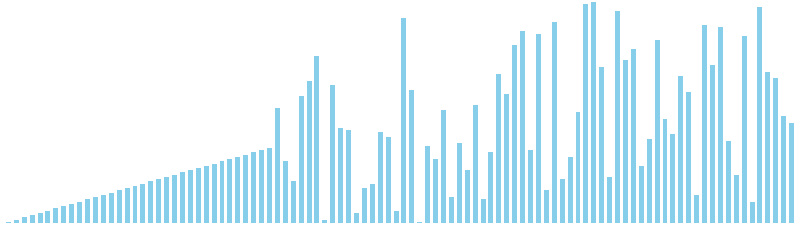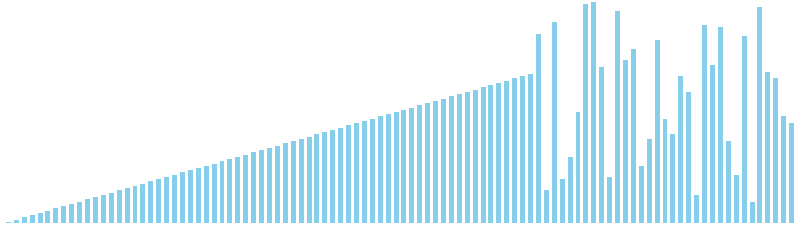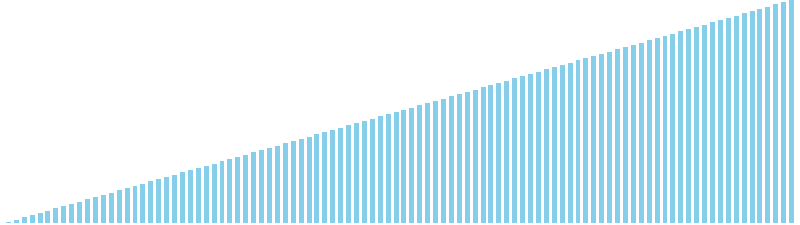
鳩の巣ソート x ランダム = 36 ns (比較: 0, 交換: 0, 書込: 100)
鳩の巣ソート x 昇順 = 39 ns (比較: 0, 交換: 0, 書込: 100)
鳩の巣ソート x 降順 = 39 ns (比較: 0, 交換: 0, 書込: 100)
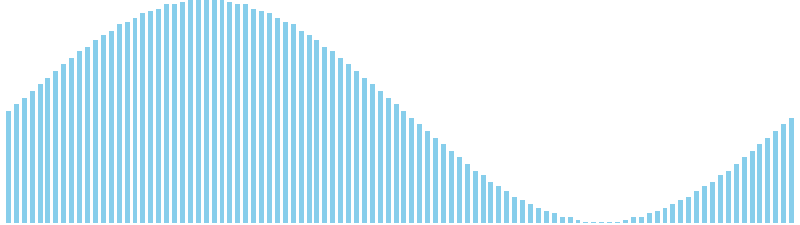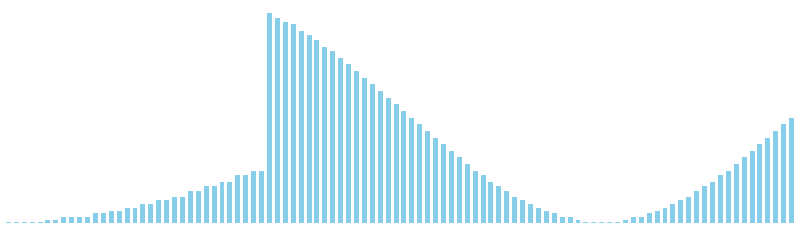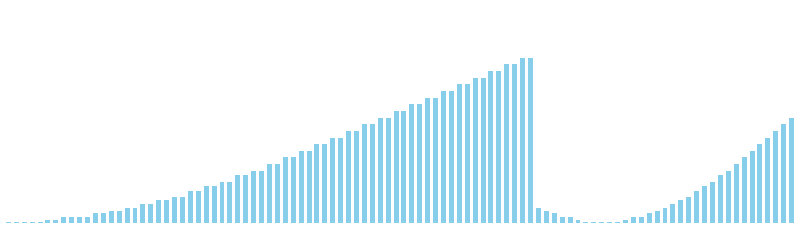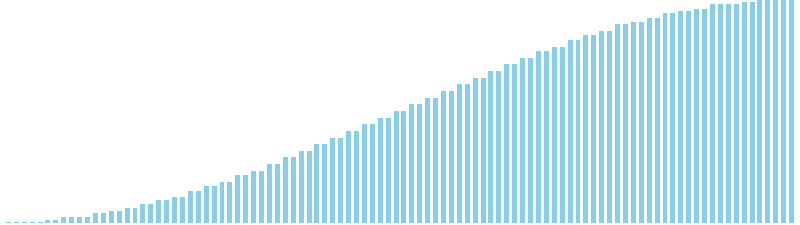
鳩の巣ソート x sin = 80 ns (比較: 0, 交換: 0, 書込: 100)
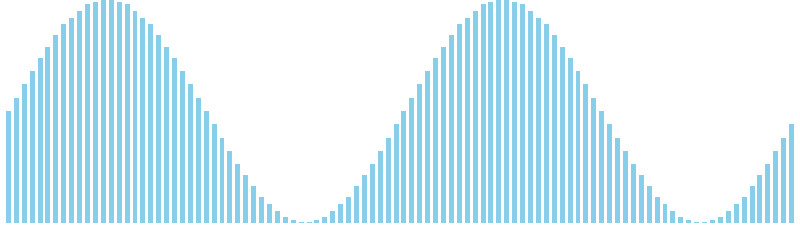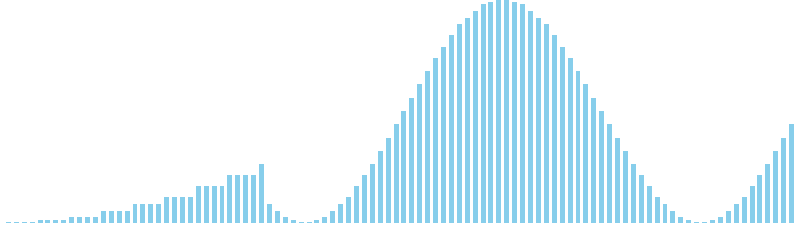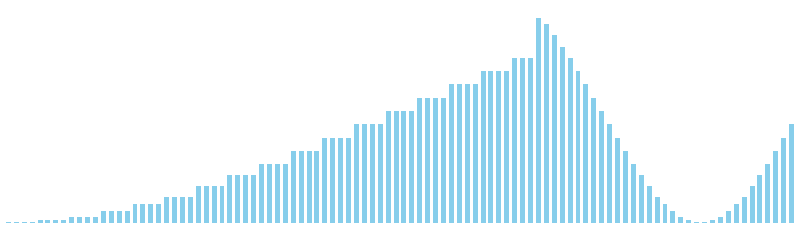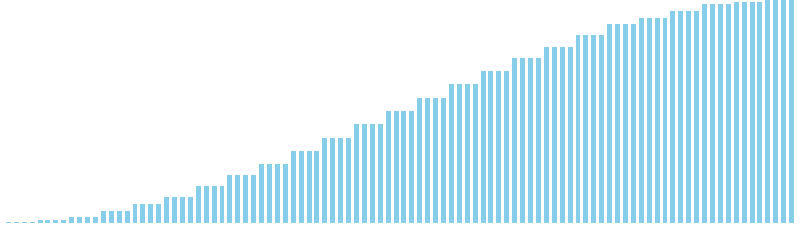
鳩の巣ソート x sin(2θ) = 37 ns (比較: 0, 交換: 0, 書込: 100)
10進基数ソート
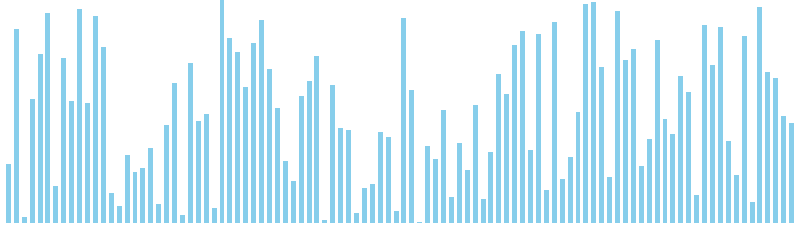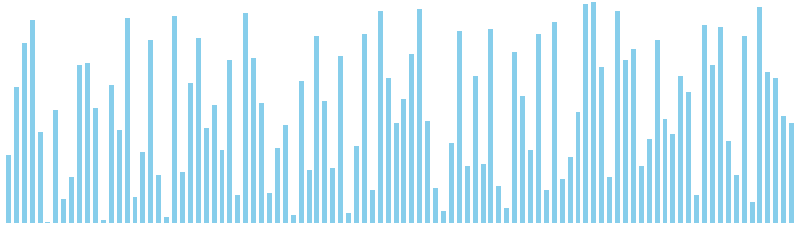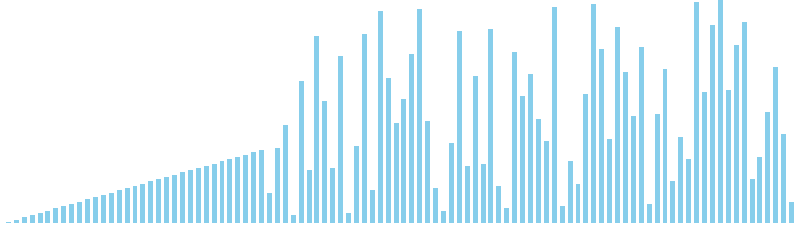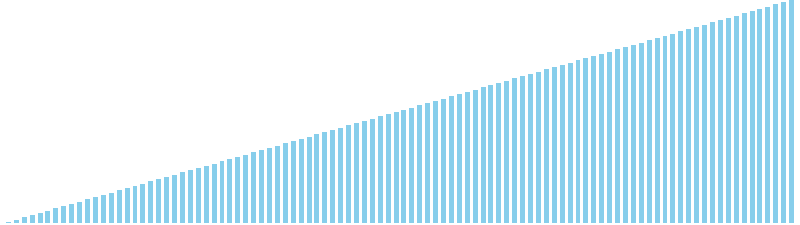
10進基数ソート x ランダム = 55 ns (比較: 0, 交換: 0, 書込: 200)
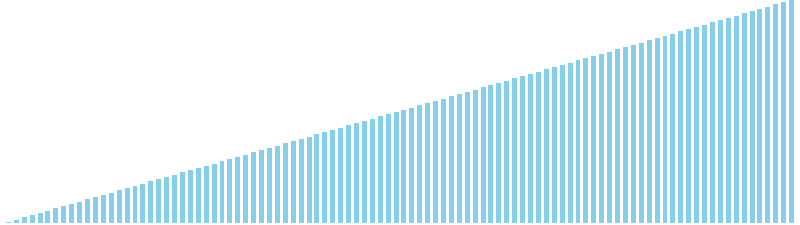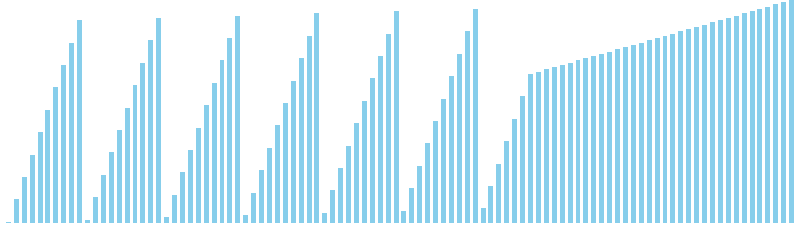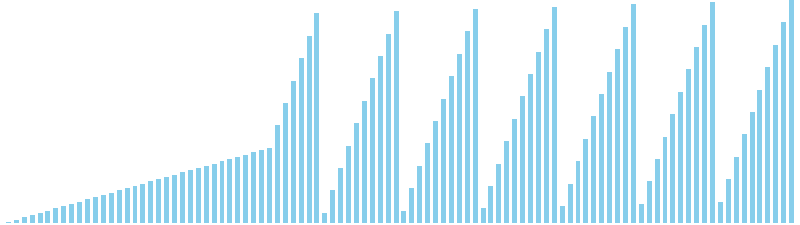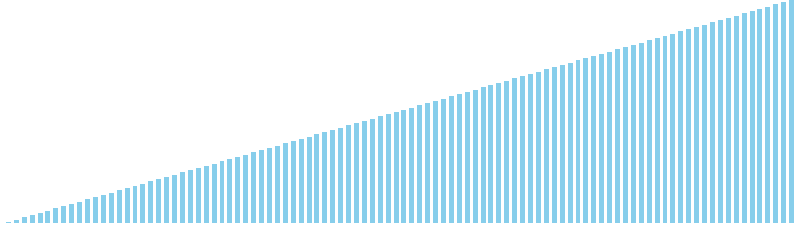
10進基数ソート x 昇順 = 54 ns (比較: 0, 交換: 0, 書込: 200)
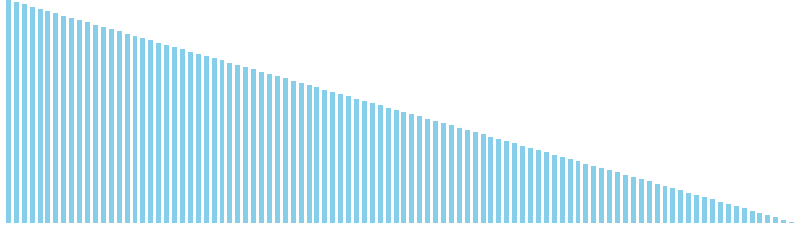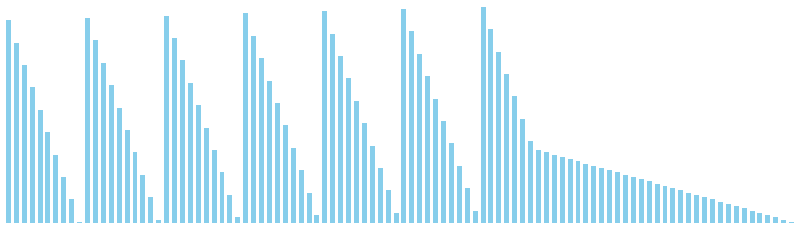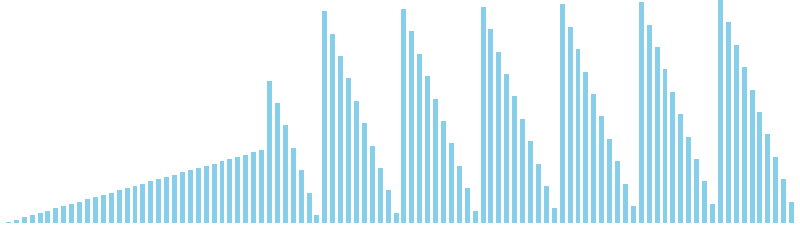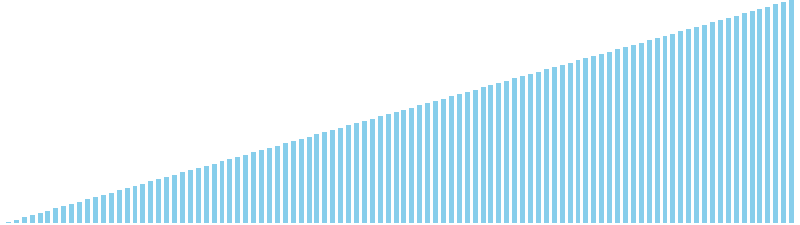
10進基数ソート x 降順 = 54 ns (比較: 0, 交換: 0, 書込: 200)
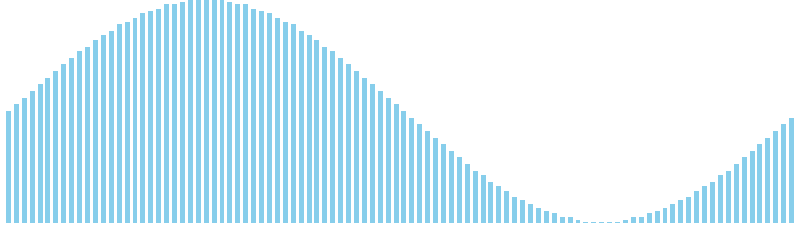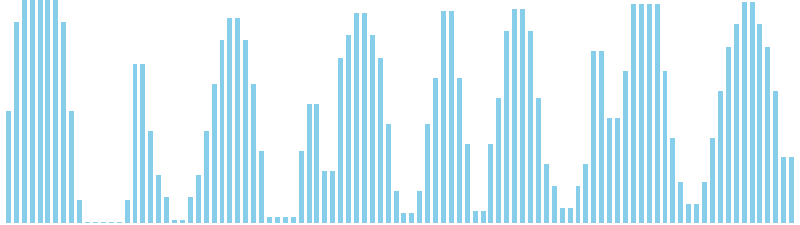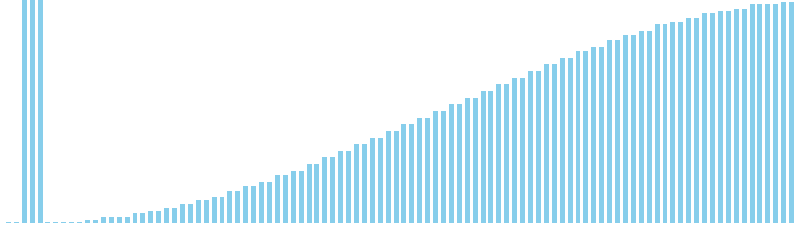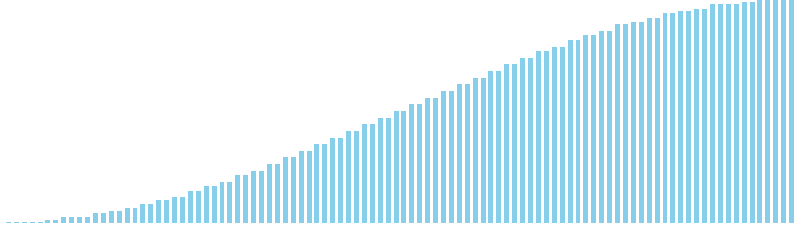
10進基数ソート x sin = 82 ns (比較: 0, 交換: 0, 書込: 300)
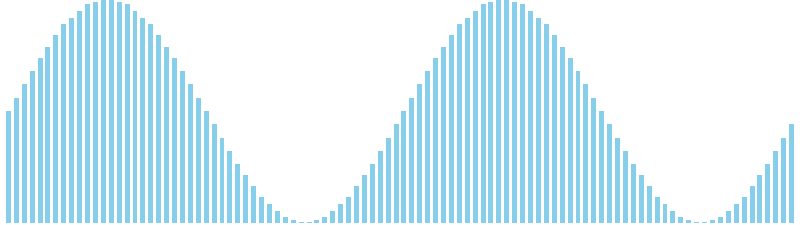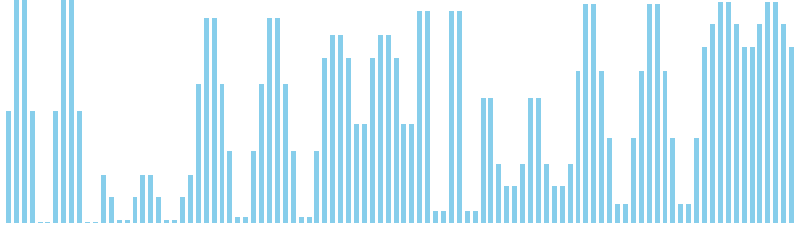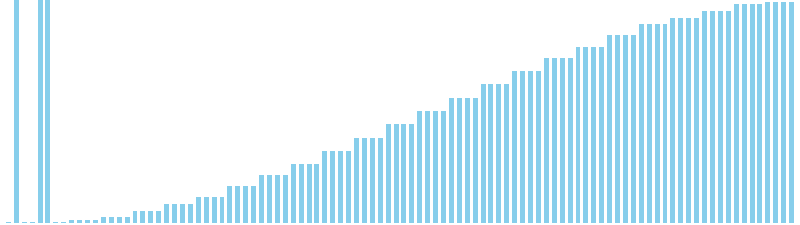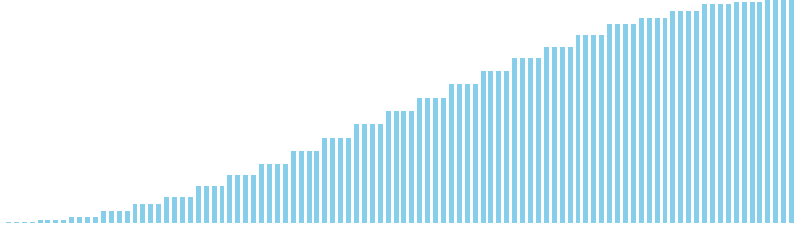
10進基数ソート x sin(2θ) = 84 ns (比較: 0, 交換: 0, 書込: 300)
256進基数ソート
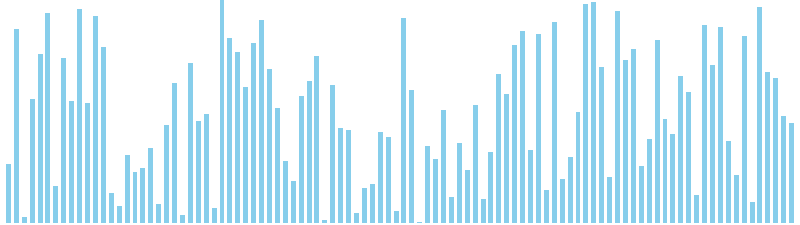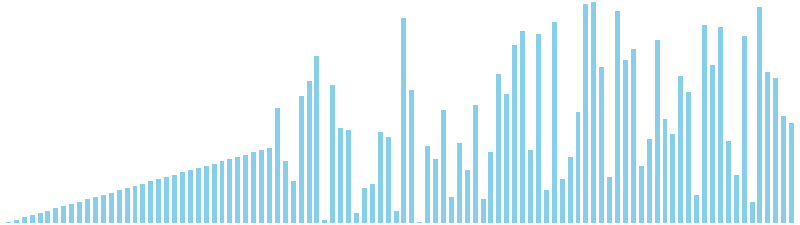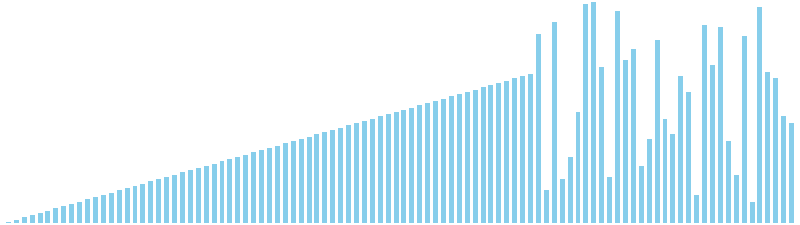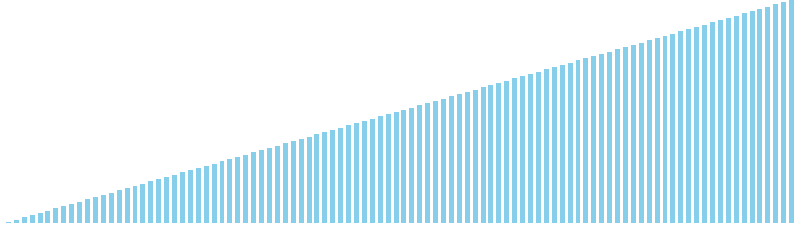
256進基数ソート x ランダム = 49 ns (比較: 0, 交換: 0, 書込: 100)
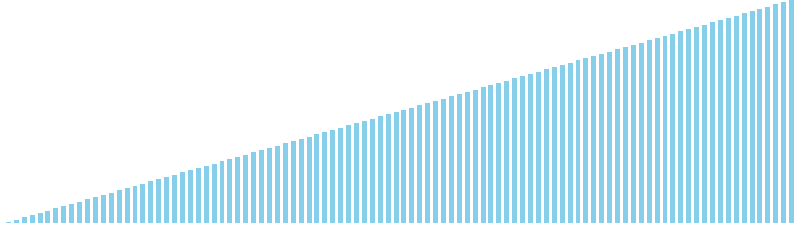
256進基数ソート x 昇順 = 48 ns (比較: 0, 交換: 0, 書込: 100)
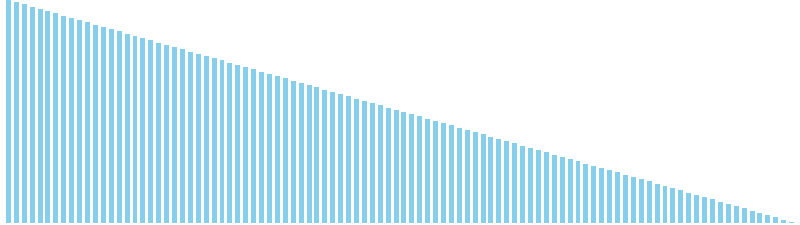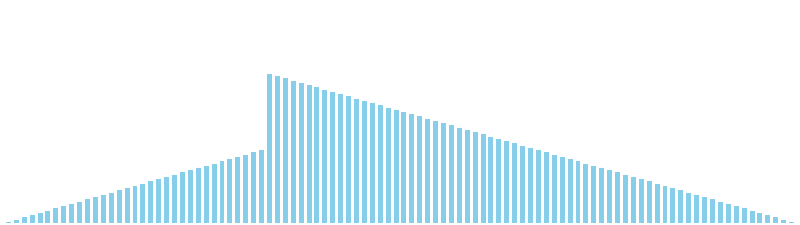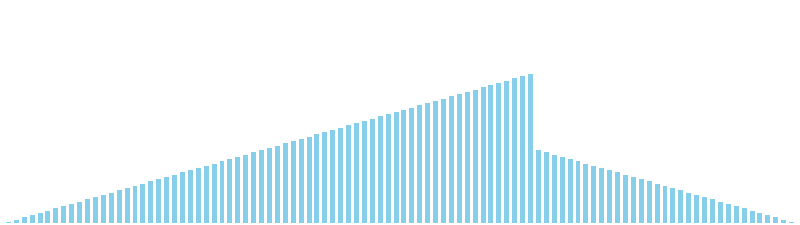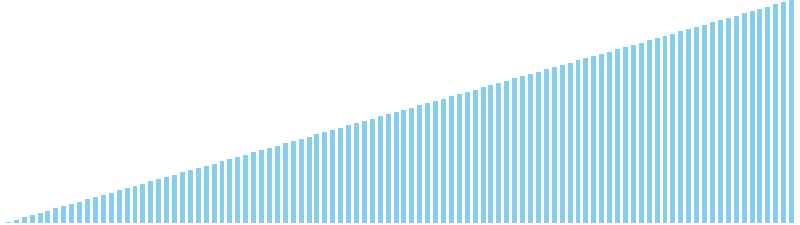
256進基数ソート x 降順 = 52 ns (比較: 0, 交換: 0, 書込: 100)
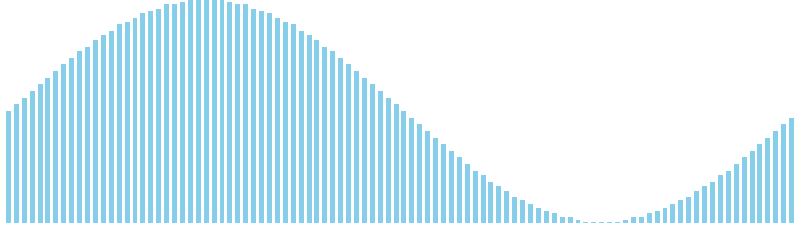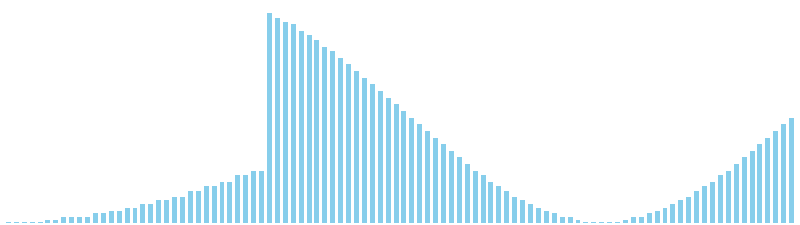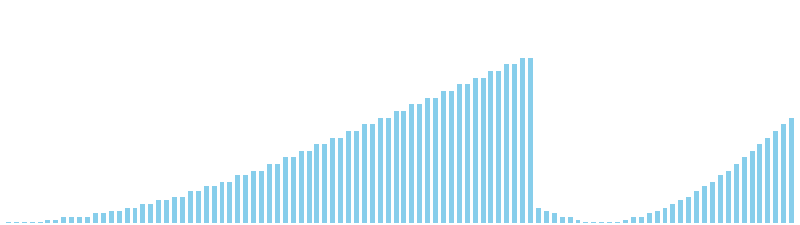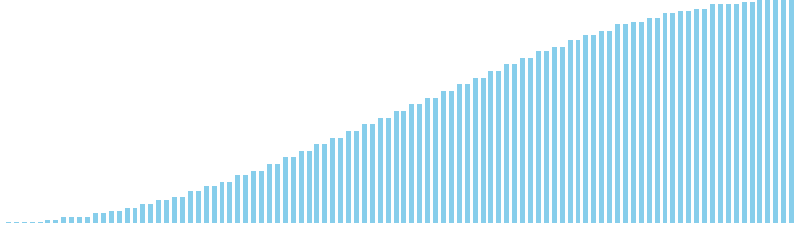
256進基数ソート x sin = 86 ns (比較: 0, 交換: 0, 書込: 100)
256進基数ソート x sin(2θ) = 49 ns (比較: 0, 交換: 0, 書込: 100)
10進基数ソート改
10進基数ソート改 x ランダム = 63 ns (比較: 0, 交換: 0, 書込: 200)
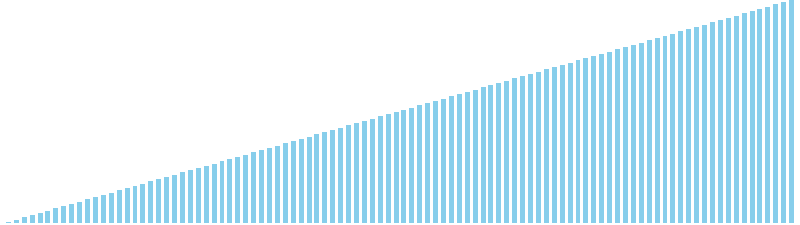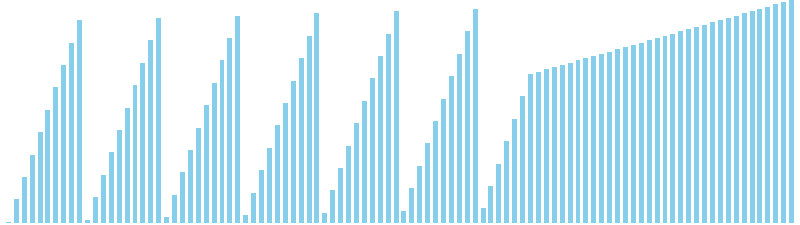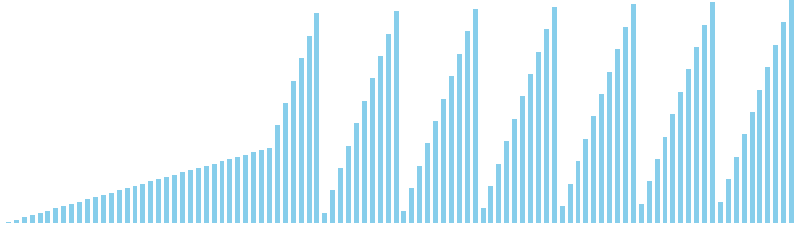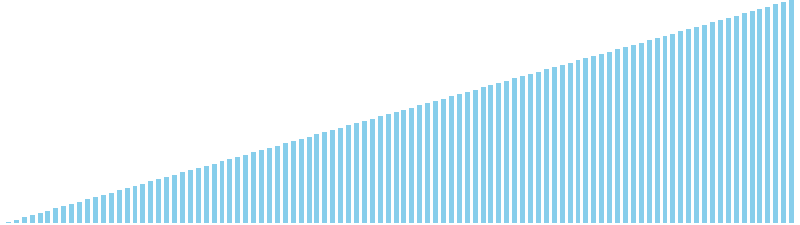
10進基数ソート改 x 昇順 = 57 ns (比較: 0, 交換: 0, 書込: 200)
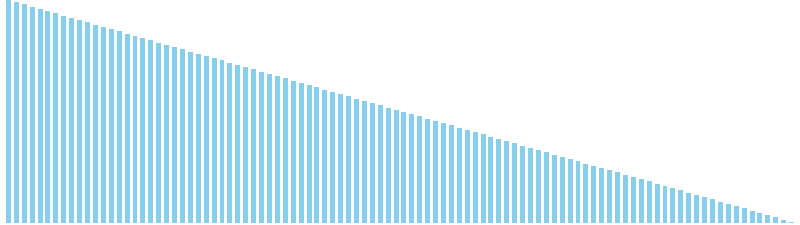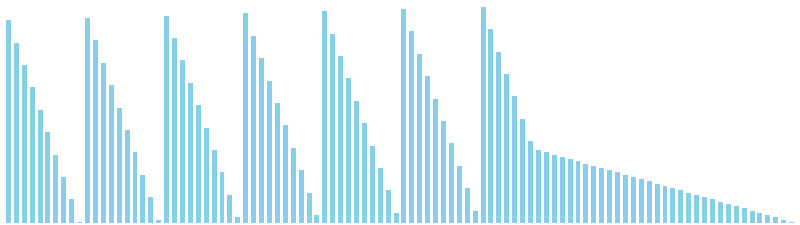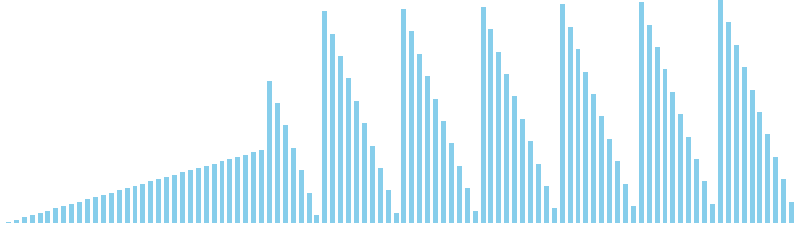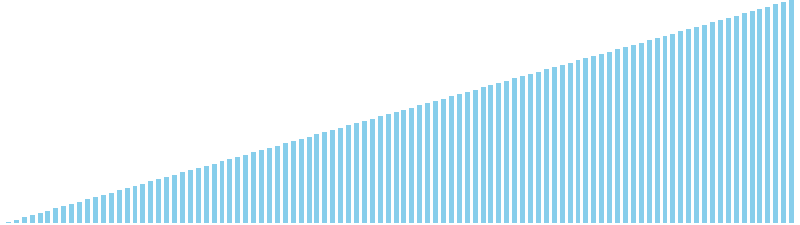
10進基数ソート改 x 降順 = 60 ns (比較: 0, 交換: 0, 書込: 200)
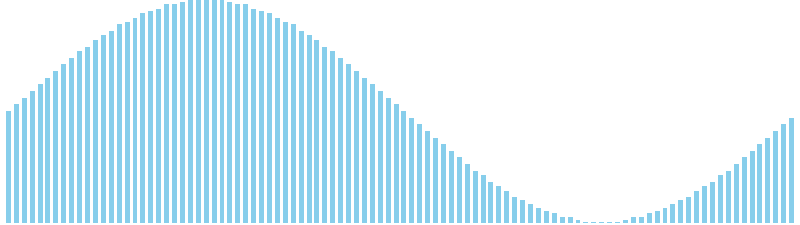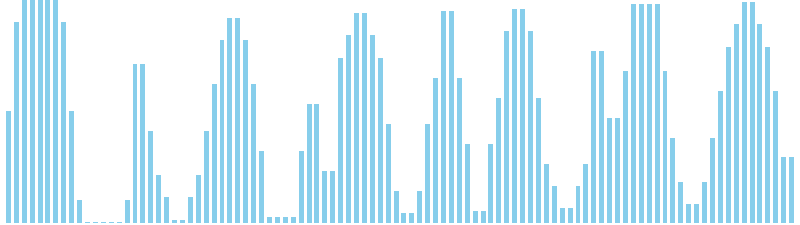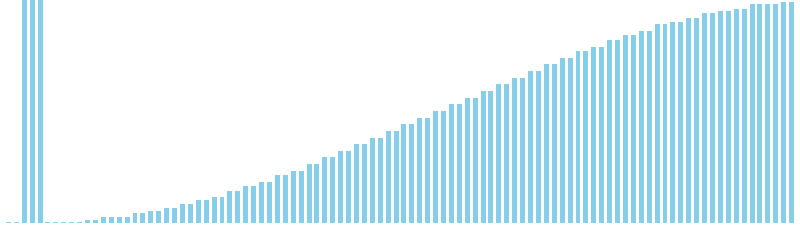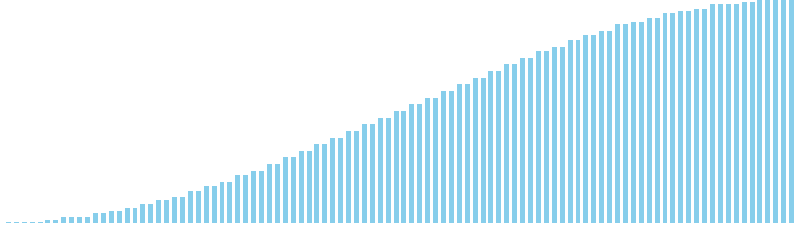
10進基数ソート改 x sin = 84 ns (比較: 0, 交換: 0, 書込: 300)
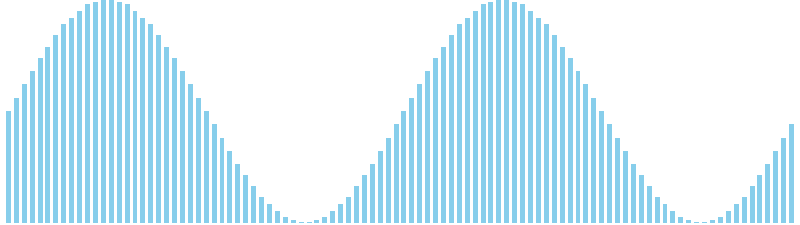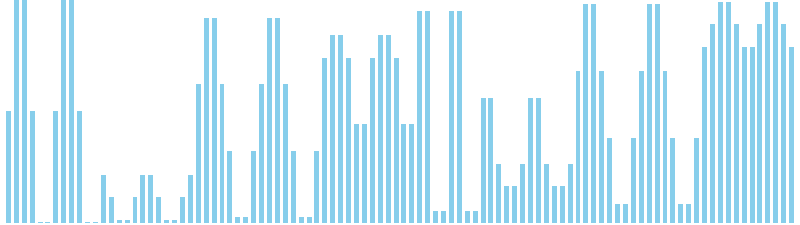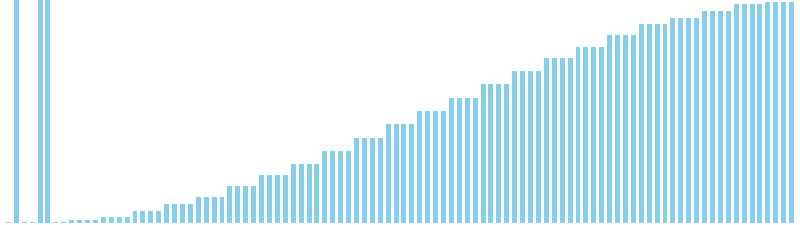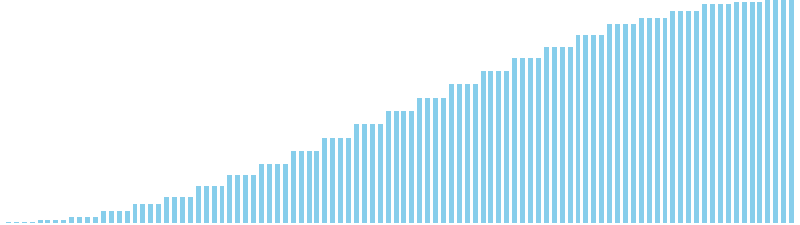
10進基数ソート改 x sin(2θ) = 86 ns (比較: 0, 交換: 0, 書込: 300)
バケットソート亜種
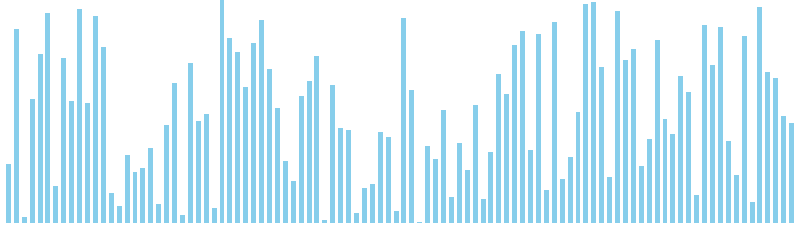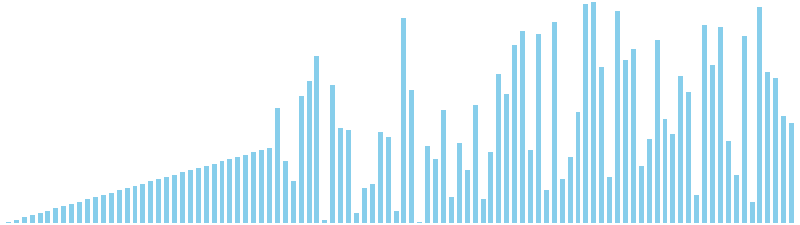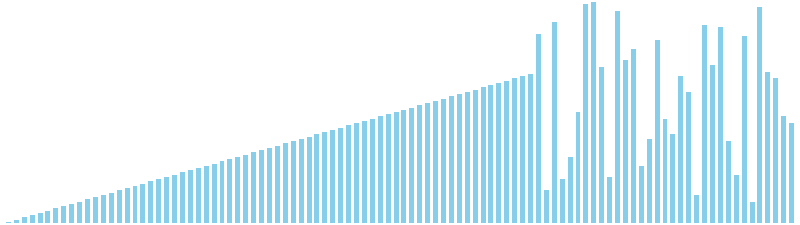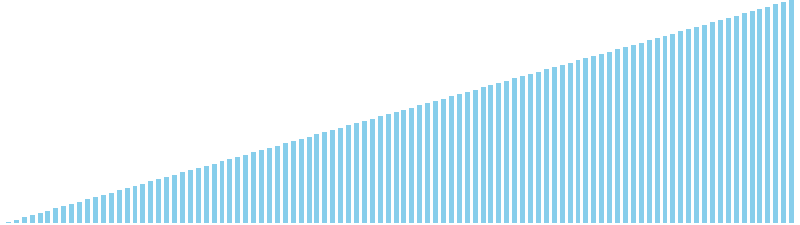
バケットソート亜種 x ランダム = 36 ns (比較: 0, 交換: 0, 書込: 100)
バケットソート亜種 x 昇順 = 36 ns (比較: 0, 交換: 0, 書込: 100)
バケットソート亜種 x 降順 = 35 ns (比較: 0, 交換: 0, 書込: 100)
バケットソート亜種 x sin = 37 ns (比較: 0, 交換: 0, 書込: 100)
バケットソート亜種 x sin(2θ) = 32 ns (比較: 0, 交換: 0, 書込: 100)
Discussion