Zenn
Luup Developers BlogPublicationへの投稿
📊

エリア面積計算の多面的アプローチ

Luup Developers
2022/11/10に公開
Python
#
map
algorithm
#
Data Science
#
Luup
tech

こんにちは！

LuupのData Strategy部（Data Scienceチーム所属）の大島です。ここでは、LuupのData Scienceチームと、Luupのデータ分析の醍醐味である地理空間データを使ったポート密度に関する分析をご紹介します。

LuupのData Scienceチームの紹介

Luupの事業では、電動アシスト自転車や電動キックボードを停めるポートの獲得、アプリや車両などのプロダクトの設計・開発・運用、車両の充電・再配置といったオペレーション、社会への発信・広報活動など、様々な取り組みが必要です。これらの取り組みをデータドリブンで推進していくのがLuupのData Scienceチームの主な役割です。

Data Strategy部内には、大きくデータパイプラインの設計・開発や運用フローの構築などに関連する業務を行うData Engineeringチームと、モデリングや機械学習、仮説検証、データ可視化などに関連する業務を行うData Scienceチームに分かれており、互いに連携を取りながら仕事をしています。

Data Engineeringチームでも既に記事を出しているので、こちらも是非読んでみてください！

冪等性を担保したGoogle Cloud Composerの設計と実装

Data Scienceチームでは、アプリや車両から取得されるデータやライド情報のデータなどに加え、公的機関が公開している外部データなど豊富なデータを活用しています。特に、地理空間データを多く利用するところが、LuupのData Scienceチームのユニークなところです。

データの可視化・ダッシュボード構築はもちろん、機械学習、クラスタリング、効果検証、ネットワーク分析、シミュレーションなど様々な手法をフルに活用して、事業に貢献しています。

今回は、地理空間データを用いたポート密度の算出に関する分析をご紹介します。

何のためにポート密度の算出をするのか？

Luupの事業において、電動アシスト自転車や電動キックボードを停められるポートは乗車・降車の起点となり非常に重要です。ユーザーの方々により便利なサービスを提供するためには、ポートが足りていない場所をきちんと把握した上でポートを増やしていくことが必要となります。

Luup-port-picture

ポートの足りていない場所を把握するには下図のように地図上で見ていくことも重要な一方、定量的にポートの多いエリアや低いエリアを把握できると議論がしやすくなります。そのために便利なのが、ポート密度の算出です。

Luup-port-map

ポート密度は、空間を一定のエリアごとに区切ってエリア間で比較することでその真価を発揮します。四角形や六角形のメッシュ単位、丁目単位、クラスタリングしたクラスター単位など、エリアの区切り方は色々考えられますが、今回は一例として比較的考えやすい区単位のポート密度を考えていきます。

サービス展開面積をどう求めるか？

ポート密度を出すにあたって悩ましいのが、分母の「面積」をどう定義するかです。例えば、区によって全域でサービス展開している場合と、一部でしかサービス展開していない場合があることを考えて、ここでは「区全体の面積」ではなく、「サービス展開面積」を採用することにします。

では、「サービス展開エリア」をどう求めるかですが、ここではポートの配置状況をベースにした3通りの方法をご紹介します。それぞれ、ポートの点の集合からそれら全てを含む範囲を算出する手法です。

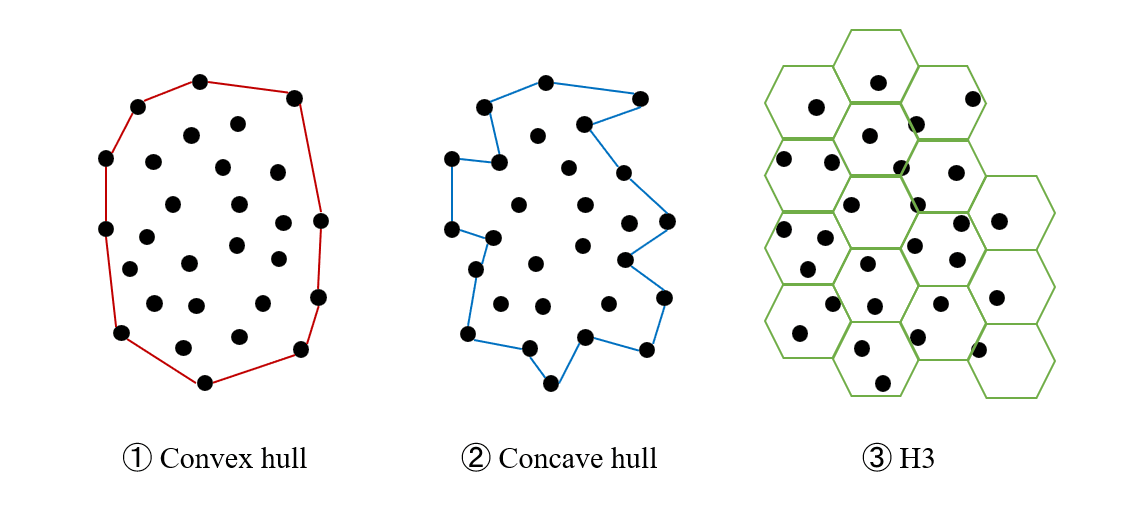
area-3-algorithms

  • ①Convex hull （凸包）：与えられた点をすべて包含する最小の凸多角形
  • ②Concave hull （凹包）：凸多角形であるConvex hullに対して、Concave hullは凹みも許した多角形（アルゴリズムのパラメーターによって凹みの程度が変わる）
  • ③H3：六角形をグリッドとして地球の表面を覆うシステム。六角形のうち、ポートの存在するものの集合をサービス展開エリアとする

これらの3つの手法それぞれで「サービス展開面積」を算出してポート密度を求めることができます。なお、①のConvex hullについてはエリアが一意に定まりますが、②のConcave hullは凹ませ具合についてのパラメーター、③のH3は六角形の大きさについてのパラメーターによって結果が変わってきます。

ここからは3つのアプローチそれぞれの特徴や手法の詳細についてご紹介していきます。

①Convex hull(凸包)

Convex hullは与えられた点をすべて包含する最小の凸多角形です。板にさした釘の上に輪ゴムを張ってできる図形とイメージすると分かりやすいと思います。ポートを全て含むConvex hullを求めて、面積を計算していきます。

Convex-hull-algorithm

Convex hullの求め方は様々な手法がありますが、代表的なのは「ギフト包装法」という手法です。上図のように、端にある点からスタートして角度を見ながら外側の点を繋いで外縁一周を囲んでいくことで凸多角形を求める手法です。

実務的には各言語で用意されているライブラリーや関数を使用するとすぐにConvex hullとその面積を求めることができます。例えば、Pythonではscipy.spatialというライブラリーでConvex hullが利用でき、BigQueryではST_CONVEXHULLという関数が用意されています。

ここでは、BigQueryでの実装例をご紹介します。

with port_table as(
  select
    port_id,
    lat,
    lng,
    concat(lng," ", lat) as lng_lat,
    ward
  from master_port
  where city= "tokyo"
)

,multipoint_table as(
  select
    ward,
    count(port_id) as num_port,
    st_geogfromtext(concat("MULTIPOINT(",string_agg(lng_lat, ","), ")") ) as multipoint
  from port_table
  group by 1
)

select
  ward,
  num_port,
  st_area(st_convexhull(multipoint)) as convex_area,
  st_area(st_convexhull(multipoint)) / num_port as convex_density
from multipoint_table
order by 4 desc

上記のようなクエリでConvex hullを用いて区ごとにサービス展開エリアを算出した結果を可視化したのが下図になります。

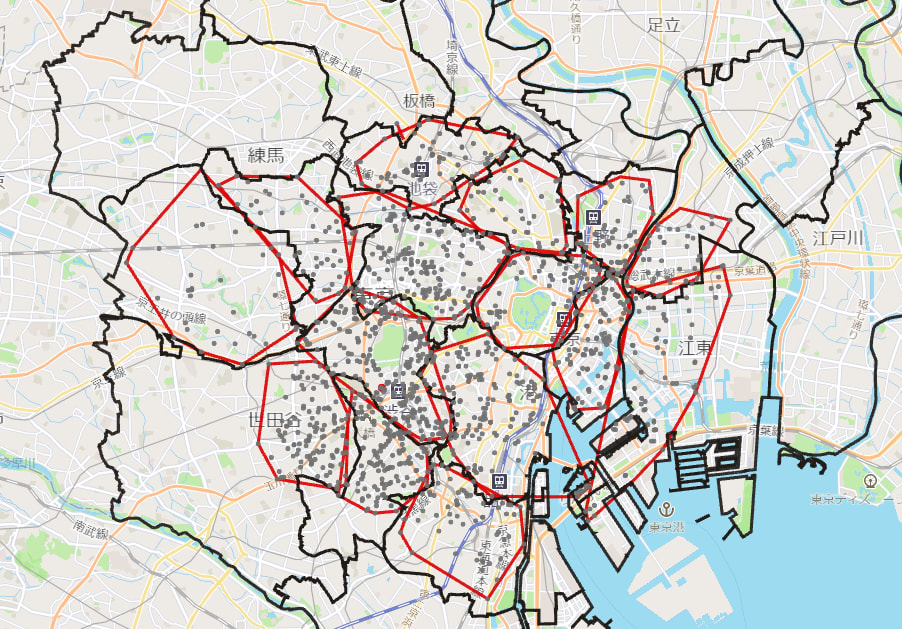
Convex-hull-map

左下の世田谷区や右の江東区のように区の一部しかポートがないエリアでは、ポートの配置をベースにしてサービス展開エリアを抽出できていることがわかります。一方、凹みがないため一部区からはみ出してしまっているものがあります。

②Concave hull(凹包)

①でご紹介したConvex hullは凹みのない凸多角形を求めるものでした。一方、②のConcave hullは凹みも許した多角形を求めるものになります。

凹みありでエリアを区切りたい場合、飛び地の点が多くある場合などには①よりも有用なことが多く、①と比べて面積が同じか小さくなるという特徴があります。

Concave hullについても求め方は様々なアプローチがありますが、代表的なのはMoreira et al.(2007)による論文により提案されたk-NN（k近傍法）を利用したアプローチです。①で紹介した「ギフト包装法」は今いる点から残り全ての点を対象に角度を調べて点を結んでいましたが、それを近くのk個のみを対象にしたのがこの手法とイメージすると分かりやすいかもしれません。アルゴリズムの詳細については、論文をご参照ください。

なお、Concave hullはパラメーターkによって凹みの程度が変わり出力結果が異なりますが、kの設定については下記2点について注意する必要があります。

  • kを小さくするほど凹みが大きくなり、kを大きくするほど凹みがなくなり①のConvex hullに近くなる。ただし、kを小さくしすぎると、飛び地の点等を飛ばして一周してしまい全ての点を含まない図形が出力されてしまう
  • kを固定した状態の時、点を増やしたのに面積が減ることがある。（外縁の点の近傍に新たに点が加わると、それに引っ張られて凹み方の形が変わる）そのため、時系列で月ごと等でポート密度の変化を算出する際には、先月のConcave hullと今月のConcave hullの和集合を取る等しないと、ポート数が増えたのにサービス展開面積が減るという一見矛盾した減少が起きてしまうことになる

上記の論文を基に実装されたConcave hullの算出アルゴリズムのコードがいくつか公開されており、そちらを活用すると比較的容易に実装することができます。

Concave hullを使って算出したサービス展開エリアは下図の通りです。①と比較すると比較的凹みがあり、区の外縁の凹みに近づいていることがわかります。

Concave-hull-map

また、一例として、港区と千代田区におけるConvex hull（緑色）とConcave hull（ピンク色）の比較を示したのが下図になります。Concave hullではポートがない部分において凹んでいるのが確認できます。

Concave-hull-example

③H3

H3は、六角形をグリッドとして地球の表面を覆うUberが開発したグリッドシステムです。正方形ではなく、中心からの距離が等しい円により近い六角形がグリッドとなっています。六角形のうち、ポートの存在するものの集合をサービス展開エリアとします。

①②と比較したこの手法の特徴は、対象グリッドにポートがない場合内部に空白地帯ができるところや、ポートより外側の余白も一部含むところです。特に前者は、①②では考慮できない代々木公園や皇居などのポートがなくサービス展開していない空白地帯に対応しているという点でより現実を反映できていると考えられます。

実装はUberよりライブラリやAPIが公開されており、pythonなどの言語で利用できます。例えば、下記のように各ポートが含まれる六角形を求めることができます。

import h3

#aperture_sizeが大きいほどhexは小さくなる
APERTURE_SIZE = 8
hex_col = 'hex'+str(APERTURE_SIZE)

# ポートの緯度経度が含まれる六角形のindexを取得
df_port[hex_col] = df_port_ward.apply(lambda x: h3.geo_to_h3(x.lat,x.lng,APERTURE_SIZE),1)

#六角形の中心の緯度経度を取得
df_port['hex_lat'] = df_port[hex_col].apply(lambda x: h3.h3_to_geo(x)[0])
df_port['hex_lng'] = df_port[hex_col].apply(lambda x: h3.h3_to_geo(x)[1])

# グリッド単位でのポート数の集計
df_hex= df_port.groupby(hex_col).size().to_frame('cnt').reset_index()
df_hex['hex_lat'] = df_hex[hex_col].apply(lambda x: h3.h3_to_geo(x)[0])
df_hex['hex_lng'] = df_hex[hex_col].apply(lambda x: h3.h3_to_geo(x)[1])
df_hex["polygon"] = df_hex.apply(lambda x: h3.h3_set_to_multi_polygon([x.hex8], geo_json=False),1)

パラメーターの設定により六角形の大きさは変化します。パラメーター設定と六角形の面積の関係はこちらにまとまっています。

h3を利用した区ごとのサービス展開エリアを可視化したのが下図になります。なお、1つの六角形の中に隣接する2つの区でポートがある場合、重複してカウントされます。

h3-map

皇居などの空白地帯を一定考慮できている一方、左の杉並区のようにポートが点在している区では、サービス展開エリアの六角形も点在した形になっており連続したエリアとはなっていません。

3手法によるポート展開密度の算出結果

3手法によって算出した、2022年でのある時点でのポート密度［ポート数/平方km］をまとめたのが下図です。（Convex hullでのポート密度が高い順に並べ替え）

result

区ごとに見ると、A,B,C区ではポート密度がかなり高くなっておりLuupの利便性が上がっている一方、M,N,O区などではまだまだ向上の余地があります。

手法ごとに比較すると、凹みがあり面積が小さくなるため、Concave hullの密度が多くの区で3手法で一番大きくなっています。

今回の分析の発展の方向性

今回は一例として、区の単位でのポート密度の算出をご紹介しました。今回の分析を起点とした発展の方向性として、最後に下記の3つについてご紹介します。

1.密度算出の精緻化の方法

2.今回の3手法以外のポート密度算出アプローチ

3.ポート密度算出手法の応用

1. 密度算出の精緻化の方法

今回は詳細を割愛しますが、次の2点を考慮することでより精緻なエリア・面積を算出できると考えられます。理論的な手法を活用するだけでなく、それを現実の理解と組み合わせて修正していくことが、リアルに近い結果を出すためには重要です。

  • A.今回算出したエリアでは一部区をはみ出してしまっている部分があるので、区との共通部分を取る
  • B.皇居や代々木公園のように、電動アシスト自転車や電動キックボードで走行不可なエリアを除く

2. 今回の3手法以外のポート密度算出アプローチ

今回は3つのアプローチを一例として紹介しましたが、別のアプローチを取ることも可能です。例えば、今回は「サービス展開エリア」をポートの配置場所を基準に考えていきましたが、「ユーザーがライドで通過しているエリア」ともう少し広く捉えてポート密度を算出することもできます。

  • 今回と同様に「ポートのデータ」を起点に考える場合、①Convex hullなどで算出したポートの展開しているエリアの外縁に数百メートル程度幅を取るというのが一つの簡易的なアプローチです
  • より本格的なアプローチとしては、「ライドデータ」を起点にユーザーがライドで通過している場所の情報などを基にサービス展開エリアを探っていくというのも考えられます

3.ポート密度算出手法の応用

今回の分析を起点にした応用例については次のようなものが考えられます。

  • ポートのクラスタリングを行い、区単位よりも細かいクラスター単位でポート密度の傾向を見てみたり、算出したポート密度と他の指標（e.g.売上、初回ライドユーザー数）との関係性を見ていく
  • 「ポート密度」の代わりに「車両配置密度」など別のものの密度を見てみる。「ポート密度」はポート配置の観点で重要ですが、「車両配置密度」は車両配置のオペレーションの観点で役に立つはずです
  • 類似のモビリティサービス（例えば、バス停の密度など）と密度を比較してみることで、他のインフラと比較してどの程度「街のインフラ」となっているのかを見ることができます

おわりに

ちょっと長めの文章でしたが、最後まで読んで下さりありがとうございます！Luupでのデータ活用の一例をご紹介しましたがいかがでしたでしょうか。

LuupのData Scienceチームでは、地理空間データを含む大量のデータをデータサイエンスの手法とかけ合わせて、事業価値に貢献していくチャレンジがたくさんあります。常に新しい取り組みがあり、どれだけやっても飽きない楽しい環境です。

もしLuupでのデータ分析、データ活用に少しでもご興味がある方がいらっしゃればお気軽にご連絡をお待ちしております。

Luup採用情報

Luup Developers Blog
Luup Developers BlogPublication

電動キックボードや小型電動アシスト自転車など、電動マイクロモビリティのシェアサービス「LUUP」を展開するLuupのテックブログです。【エンジニア採用中】recruit.luup.sc

Discussion