🔮

量子アニーリングを使って魔方陣を作ってみた

2025/03/02に公開

Python

はじめに

オンライン公開伴走型量子コンピューティング講座QA4U2卒業生のluna_moonlightです。この記事では、量子アニーリングを用いた魔方陣の生成について解説していきます。

量子アニーリングとは

量子アニーリングとは、量子ゆらぎと呼ばれる現象を用いた組合せ最適化問題^[1]を解く手法です。

組合せ最適化問題を解く古典的な手法のひとつとして、焼きなまし法というアルゴリズムがあります。焼きなまし法では、温度というパラメータを導入し、最初は高温に設定して局所解を脱しながら解を探索していき、徐々に温度を低くしていくことで最適解へ遷移していきます。量子アニーリングは、温度の代わりに量子ゆらぎを導入して最適解を探索するアルゴリズムとして、1998年に"Quantum annealing in the transverse Ising model"という論文で門脇正史と西森秀稔により提案されました。

魔方陣

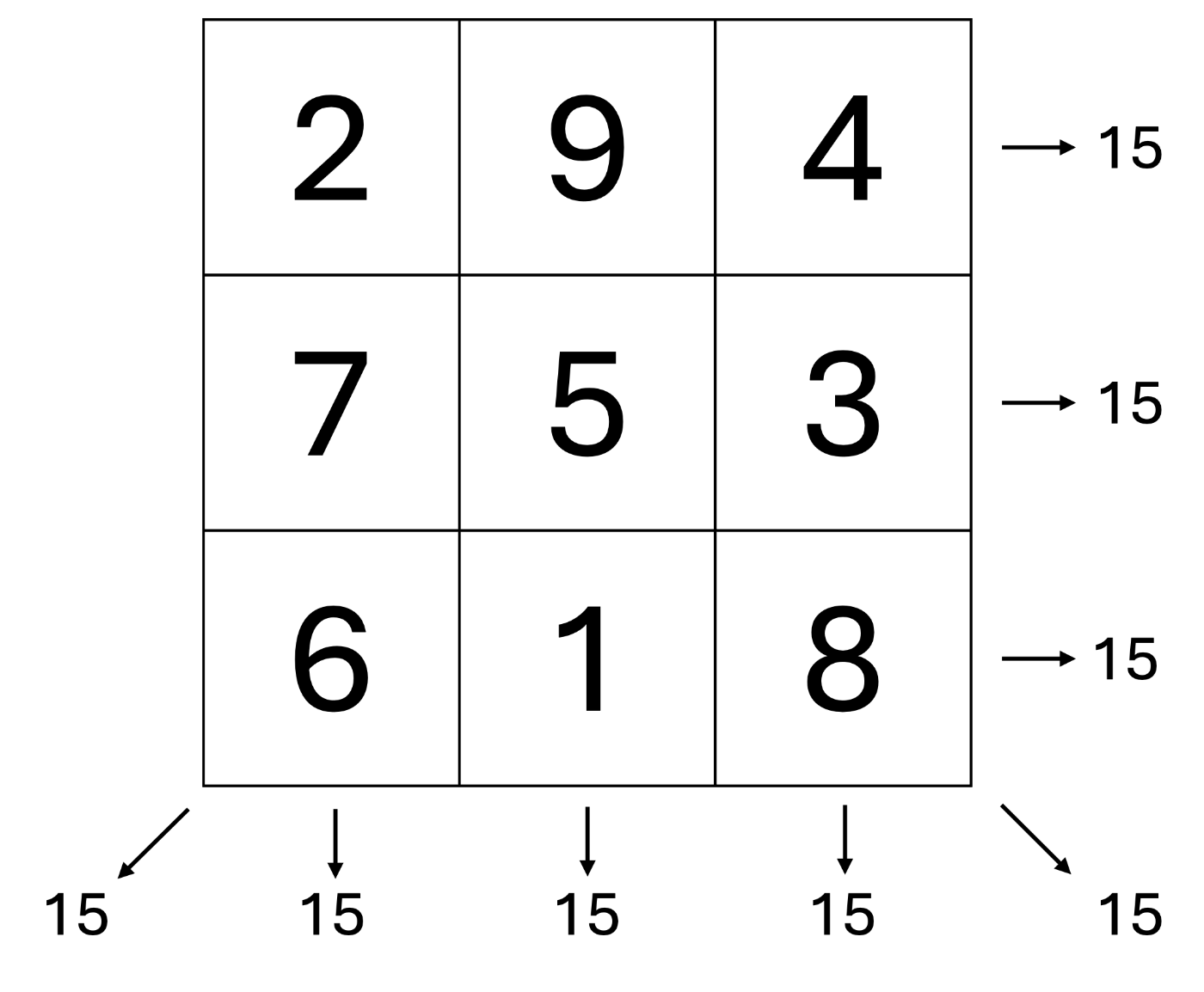
魔方陣とは、 $N \times N$ の各マスに $1 \sim N^2$ までの数字をちょうどひとつずつ入れて、縦横斜めのどの列についても、その列の総和が等しくなるようなものです。例えば $3 \times 3$ の魔方陣は以下のようになり、縦横斜めのどの列も総和が15になっています。

$3 \times 3$ は対称な形を除いて1通り、 $4 \times 4$ は880通り、 $5 \times 5$ は275305224通り、 $6 \times 6$ は17753889197660635632通り存在することが知られています。

量子アニーリングで魔方陣を解いてみる

それでは実際に量子アニーリングを用いて魔方陣生成を実装していきます。

定式化

量子アニーリングで解けるようにするには、非制約二値変数二次最適化(QUBO: Quadratic Unconstrained Binary Optimization)の形に落とし込む必要があります。QUBOでは、 $0$ と $1$ の2つの値をとる $M$ 個のbinary変数 $x_1, x_2, \dots, x_M$ に対して、二次形式の評価関数 $f:\{0, 1\}^M \to \Reals$ を最小にするように変数の組み合わせ $\bm{x}=(x_1, x_2, \dots, x_M)$ を求めていきます。すなわち、

f(\bm{x})=\bm{x}Q\bm{x}^T=\sum_{i=1}^M\sum_{j=1}^M Q_{i,j}x_ix_j

を最小にする $\bm{x}=(x_1, x_2, \dots, x_M)$ を求めます。ここで、行列 $Q \in \Reals ^ {M \times M}$ は、対角成分は $x_i$ の重みを、非対角成分は $x_i, x_j$ 成分の相互作用を表しており、QUBO行列と呼ばれます。

ここで、魔方陣生成について考えてみましょう。 $x_{i,j,n}$ は、上から $i$ 行目、左から $j$ 列目のマスを $n \in \{1, 2, \dots, N^2\}$ にするか否かを表すこととします。例えば、上から2行目、左から1列目のマスを7場合は $x_{2,1,7}=1$ に、上から1行目、左から3列目のマスを5にしない場合は $x_{1,3,5}=0$ になります。 $N \times N$ の魔方陣を生成する場合の変数の組み合わせは、

\bm{x}=(x_{1,1,1}, x_{1,1,2}, \dots, x_{1,1,N}, x_{1,2,1}, \dots, x_{1, N, N}, x_{2,1,1}, x_{2,1,2}, \dots, x_{i,j,1}, x_{i,j,2}, \dots, x_{N, N, N})

となります。量子アニーリングで解けるような形に落とし込むために、この組み合わせ $\bm{x}$ が正しい魔方陣を生成するときは小さな値を、間違った魔方陣を生成するときは大きな値をとるように評価関数 $f$ (QUBO行列 $Q$ )を決定していきます。

1.各列の総和は等しい

魔方陣は、縦横斜めのどの列についてもその列の総和が等しくなるという制約があります。この制約は以下のように表すことができます。

\begin{split} f_0(\bm{x}) &=\sum_{k}\sum_{l}\left(\sum_{(i, j) \in L_k}\sum_{n} nx_{i,j,n} - \sum_{(i, j) \in L_l}\sum_{n} nx_{i,j,n}\right)^2\\ &=\sum_{k}\sum_{l}\left(\sum_{(i_1, j_1) \in L_k}\sum_{(i_2, j_2) \in L_k}\sum_{n_1}\sum_{n_2} n_1n_2x_{i_1,j_1,n_1}x_{i_2,j_2,n_2} - 2\sum_{(i_1, j_1) \in L_k}\sum_{(i_2, j_2) \in L_l}\sum_{n_1}\sum_{n_2} n_1n_2x_{i_1,j_1,n_1}x_{i_2,j_2,n_2} + \sum_{(i_1, j_1) \in L_l}\sum_{(i_2, j_2) \in L_l}\sum_{n_1}\sum_{n_2} n_1n_2x_{i_1,j_1,n_1}x_{i_2,j_2,n_2}\right) \end{split}

ただし、 $L_k$ は列に含まれるマスの集合のことで、以下のようになります。 $L_0 \sim L_{N - 1}$ は横の行、 $L_N \sim L_{2N - 1}$ は縦の列、 $L_{2N}$ は右下がりの斜めの列、 $L_{2N + 1}$ は右上がりの斜めの列を表しています。

\begin{split} L_0 &= \{(1, 1), (1, 2), \dots, (1, N)\}\\ L_1 &= \{(2, 1), (2, 2), \dots, (2, N)\}\\ \vdots\\ L_N &= \{(1, 1), (2, 1), \dots, (N, 1)\}\\ L_{N + 1} &= \{(1, 2), (2, 2), \dots, (N, 2)\}\\ \vdots\\ L_{2N} &= \{(1, 1), (2, 2), \dots, (N, N)\}\\ L_{2N+1} &= \{(1, N), (2, N-1), \dots, (N, 1)\}\\ \end{split}

ある列 $k$ とある列 $l$ の総和の差を $d$ とすると、 $\left(\sum_{(i, j) \in L_k}\sum_{n} nx_{i,j,n} - \sum_{(i, j) \in L_l}\sum_{n} nx_{i,j,n}\right)^2 = d^2$ となるため $d=0$ のときに最小、すなわちすべての列の総和が等しいときに $f_0(\bm{x})$ は最小になります。

この評価関数は実装が少し複雑になるため、もう少し単純にできないか考えてみます。
魔方陣の各列の総和は簡単に求めることができます。魔法陣のマスには $1 \sim N^2$ までの数字がちょうど一度ずつ入るので、全マスの総和は $1 + 2 + \dots + N^2 = \dfrac{1}{2}N^2(N^2 + 1)$ です。縦の列(横の行)は $N$ 列あり、それらすべての総和が等しくなるので各列の総和は $\dfrac{1}{2}N^2(N^2 + 1) \cdot \dfrac{1}{N} = \dfrac{1}{2}N(N^2 + 1)$ となります。そこで、各列の総和は等しいという制約を、各列の総和は $\dfrac{1}{2}N(N^2 + 1)$ という制約で式を立てていきます。
この先は $S = \dfrac{1}{2}N(N^2 + 1)$ として議論を進めていきます。

1-1.横の行の総和は $S$

横の行の総和は $S$ という制約は以下のように表すことができます。

f_1(\bm{x})=\sum_{i}\left(\sum_{j}\sum_{n} nx_{i,j,n} - S\right)^2

\left(\sum_{j}\sum_{n} nx_{i,j,n} - S\right)^2は二次形式ではありませんが、x_{i,j,n} \in \{0, 1\}に注意すると、

\begin{split}
\left(\sum_{j}\sum_{n} nx_{i,j,n} - S\right)^2
&= \left(\sum_{j}\sum_{n} nx_{i,j,n} - S\right)\left(\sum_{j}\sum_{n} nx_{i,j,n} - S\right)\\
&= \sum_{j_1, j_2}\sum_{n_1, n_2} n_1 n_2 x_{i, j_1, n_1}x_{i, j_2, n_2} - 2\sum_{j}\sum_{n} Sn x_{i, j, n} + S^2\\
&= \sum_{j_1, j_2}\sum_{n_1, n_2} n_1 n_2 x_{i, j_1, n_1}x_{i, j_2, n_2} - 2\sum_{j}\sum_{n} Sn x_{i, j, n}x_{i, j, n} + S^2 \quad (\because x_{i,j,n}=x_{i,j,n}x_{i,j,n})
\end{split}
と変形でき、最小化問題では定数項は影響しないため、無視することで二次形式の形にできます。この項は罰金項と呼ばれ、\lambdaを罰金係数として制約の強さを調整します。

1-2.縦の列の総和は $S$

縦の列の総和は $S$ という制約は以下のように表すことができます。

f_2(\bm{x})=\sum_{j}\left(\sum_{i}\sum_{n} nx_{i,j,n} - S\right)^2

1-3.斜めの列の総和は $S$

斜めの列の総和は $S$ という制約は以下のように表すことができます。左側の項が右下がりの斜めの列に関する制約、右側が右上がりの斜めの列に関する制約になっています。

f_3(\bm{x})=\left(\sum_{d}\sum_{n} nx_{d,d,n} - S\right)^2 + \left(\sum_{d}\sum_{n} nx_{d,N - d + 1,n} - S\right)^2

2. $1 \sim N^2$ はちょうど1回しか使えない

魔方陣は、 $1 \sim N^2$ はちょうど1回しか使えないという制約があります。この制約は以下のように表すことができます。

f_4(\bm{x})=\sum_{n}\left(\sum_{i}\sum_{j} x_{i,j,n} - 1\right)^2

ある数字をちょうど1回使う場合は、 $\left(\sum_{i}\sum_{j} x_{i,j,n} - 1\right)^2 = 0$ をとり、1回も使わなかったり複数回使ったりすると0より大きな値を取ってしまうため、 $1 \sim N^2$ をちょうど1回使った時に $f_4(\bm{x})$ は最小になります。

3.各マスに1つしか数字を入れてはいけない

魔方陣は、各マスに1つしか数字を入れてはいけないという制約が暗にあります。この制約は以下のように表すことができます。

f_5(\bm{x})=\sum_{i}\sum_{j}\left(\sum_{n} x_{i,j,n} - 1\right)^2

あるマスにちょうど1つの数字を入れる場合は、 $\sum_{i}\sum_{j}\left(\sum_{n} x_{i,j,n} - 1\right)^2 = 0$ をとり、1つも入れなかったり複数入れたりすると0より大きな値を取ってしまうため、すべてのマスに数字がちょうど1つ入る時に $f_5(\bm{x})$ は最小になります。

魔方陣生成の評価関数

ここまでで、制約ひとつひとつに対して評価関数を作ってきました。これらを足し合わせることで、魔方陣生成に必要な評価関数を作ることができます。具体的には以下のようになります。

\begin{split} f(\bm{x}) &= \lambda_1 f_1(\bm{x}) + \lambda_1 f_2(\bm{x}) + \lambda_1 f_3(\bm{x}) + \lambda_2 f_4(\bm{x}) + \lambda_3 f_5(\bm{x})\\ &= \lambda_1 \sum_{i}\left(\sum_{j}\sum_{n} nx_{i,j,n} - S\right)^2 + \lambda_1 \sum_{j}\left(\sum_{i}\sum_{n} nx_{i,j,n} - S\right)^2 + \lambda_1 \left(\left(\sum_{d}\sum_{n} nx_{d,d,n} - S\right)^2 + \left(\sum_{d}\sum_{n} nx_{d,N - d + 1,n} - S\right)^2\right) + \lambda_2 \sum_{n}\left(\sum_{i}\sum_{j} x_{i,j,n} - 1\right)^2 + \lambda_3 \sum_{i}\sum_{j}\left(\sum_{n} x_{i,j,n} - 1\right)^2 \end{split}

実装

ここまでで、魔方陣生成の評価関数をQUBOの形で定式化することができました。それでは早速実装していきましょう。

まず、D-Waveの量子アニーリングマシンを使うために、D-Wave Leapでアカウントを作成します。

次に、必要な外部ライブラリをインストールしましょう。量子アニーリングを使うためにdwave-ocean-sdkをインストールします。

pip install dwave-ocean-sdk

必要な外部ライブラリをインストールしたところで、さっそくプログラムを書いていきましょう。コードの全体像はこちらです。

コードの全体像

from collections import defaultdict
from dwave.system import DWaveSampler, EmbeddingComposite


'''-----パラメータ-----'''
N = 3             # 魔方陣の一辺の大きさ
l1 = 1            # 罰金項の強さ(各列の総和は等しい)
l2 = 10           # 罰金項の強さ(各数字は1回)
l3 = 10           # 罰金項の強さ(各マスに数字は1つ)
num_reads = 1000  # アニーリングを実行する回数
token = 'XXXX'    # API token(個人のものを使用)
solver='Advantage_system6.4' # 量子アニーリングマシン
'''------------------'''

Q = defaultdict(lambda: 0) # Q_i,j,n  (i, j)に入れる値n
S = N * (N ** 2 + 1) // 2  # 各列の総和

# x_i,j,nの通し番号を記録
ijn_to_idx = {}
idx = 0
for i in range(1, N + 1):
  for j in range(1, N + 1):
    for n in range(1, N ** 2 + 1):
      ijn_to_idx[(i, j, n)] = idx
      idx += 1



# 各行の総和をSに制限
for i in range(1, N + 1):
  for j1 in range(1, N + 1):
    for n1 in range(1, N ** 2 + 1):
      for j2 in range(1, N + 1):
        for n2 in range(1, N ** 2 + 1):
          Q[(ijn_to_idx[(i, j1, n1)], ijn_to_idx[(i, j2, n2)])] += n1 * n2 * l1
      Q[(ijn_to_idx[(i, j1, n1)], ijn_to_idx[(i, j1, n1)])] -= 2 * n1 * S * l1

# 各列の総和をSに制限
for j in range(1, N + 1):
  for i1 in range(1, N + 1):
    for n1 in range(1, N ** 2 + 1):
      for i2 in range(1, N + 1):
        for n2 in range(1, N ** 2 + 1):
          Q[(ijn_to_idx[(i1, j, n1)], ijn_to_idx[(i2, j, n2)])] += n1 * n2 * l1
      Q[(ijn_to_idx[(i1, j, n1)], ijn_to_idx[(i1, j, n1)])] -= 2 * n1 * S * l1

# 斜め(右下がり)の総和をSに制限
for d1 in range(1, N + 1):
  for n1 in range(1, N ** 2 + 1):
    for d2 in range(1, N + 1):
      for n2 in range(1, N ** 2 + 1):
        Q[(ijn_to_idx[(d1, d1, n1)], ijn_to_idx[(d2, d2, n2)])] += n1 * n2 * l1
    Q[(ijn_to_idx[(d1, d1, n1)], ijn_to_idx[(d1, d1, n1)])] -= 2 * n1 * S * l1
    
# 斜め(右上がり)の総和をSに制限
for d1 in range(1, N + 1):
  for n1 in range(1, N ** 2 + 1):
    for d2 in range(1, N + 1):
      for n2 in range(1, N ** 2 + 1):
        Q[(ijn_to_idx[(d1, N - d1 + 1, n1)], ijn_to_idx[(d2, N - d2 + 1, n2)])] += n1 * n2 * l1
    Q[(ijn_to_idx[(d1, N - d1 + 1, n1)], ijn_to_idx[(d1, N - d1 + 1, n1)])] -= 2 * n1 * S * l1

# 同じ数字が重複しないように制限
for n in range(1, N ** 2 + 1):
  for i1 in range(1, N + 1):
    for j1 in range(1, N + 1):
      for i2 in range(1, N + 1):
        for j2 in range(1, N + 1):
          Q[(ijn_to_idx[(i1, j1, n)], ijn_to_idx[(i2, j2, n)])] += 1 * l2
      Q[(ijn_to_idx[(i1, j1, n)], ijn_to_idx[(i1, j1, n)])] -= 2 * l2

# 各マスにちょうど1つの数字に制限
for i in range(1, N + 1):
  for j in range(1, N + 1):
    for n1 in range(1, N ** 2 + 1):
      for n2 in range(1, N ** 2 + 1):
        Q[(ijn_to_idx[(i, j, n1)], ijn_to_idx[(i, j, n2)])] += 1 * l3
      Q[(ijn_to_idx[(i, j, n1)], ijn_to_idx[(i, j, n1)])] -= 2 * l3



# 量子アニーリングの実行
endpoint = 'https://cloud.dwavesys.com/sapi/'
dw_sampler = DWaveSampler(solver=solver, token=token, endpoint=endpoint)
sampler = EmbeddingComposite(dw_sampler)
sampleset = sampler.sample_qubo(Q, num_reads=num_reads)



# 結果に基づいて魔方陣を生成
result = [i for i in sampleset.first[0].values()]
ans = [[None] * N for _ in range(N)]
for i in range(1, N + 1):
  for j in range(1, N + 1):
    for n in range(1, N ** 2 + 1):
      if result[ijn_to_idx[(i, j, n)]] == 1:
        ans[i - 1][j - 1] = n

# 魔方陣の表示
print(*ans, sep='\n')

ここからは、このコードを分けて解説していきます。

初期化

以下のコードは、必要なライブラリのインポートや変数、定数を定義しています。パラメータと書かれている部分を変更することで、魔方陣の大きさや使う量子アニーリングマシンなどを変更することができます。
また、DWaveSamplerでは $x_{i,j,n}$ のような多変数は扱いにくいため、 $x'_k (k = 0, 1, \dots)$ のような0始まりの変数に変換しています。

from collections import defaultdict
from dwave.system import DWaveSampler, EmbeddingComposite


'''-----パラメータ-----'''
N = 3             # 魔方陣の一辺の大きさ
l1 = 1            # 罰金項の強さ(各列の総和は等しい)
l2 = 10           # 罰金項の強さ(各数字は1回)
l3 = 10           # 罰金項の強さ(各マスに数字は1つ)
num_reads = 1000  # アニーリングを実行する回数
token = 'XXXX'    # API token(個人のものを使用)
solver='Advantage_system6.4' # 量子アニーリングマシン
'''------------------'''

Q = defaultdict(lambda: 0) # Q_i,j,n  (i, j)に入れる値n
S = N * (N ** 2 + 1) // 2  # 各列の総和

# x_i,j,nの通し番号を記録
ijn_to_idx = {}
idx = 0
for i in range(1, N + 1):
  for j in range(1, N + 1):
    for n in range(1, N ** 2 + 1):
      ijn_to_idx[(i, j, n)] = idx
      idx += 1

QUBO行列 $Q$ の設定

ここでは、定式化した魔方陣生成の評価関数をプログラムに載せています。

1.各列の総和は等しい

以下のコードは、 $f_1(\bm{x}) = \sum_{i}\left(\sum_{j}\sum_{n} nx_{i,j,n} - S\right)^2$ , $f_2(\bm{x}) = \sum_{j}\left(\sum_{i}\sum_{n} nx_{i,j,n} - S\right)^2$ , $f_3(\bm{x}) = \left(\sum_{d}\sum_{n} nx_{d,d,n} - S\right)^2 + \left(\sum_{d}\sum_{n} nx_{d,N - d + 1,n} - S\right)^2$ に対応しています。

# 各行の総和をSに制限
for i in range(1, N + 1):
  for j1 in range(1, N + 1):
    for n1 in range(1, N ** 2 + 1):
      for j2 in range(1, N + 1):
        for n2 in range(1, N ** 2 + 1):
          Q[(ijn_to_idx[(i, j1, n1)], ijn_to_idx[(i, j2, n2)])] += n1 * n2 * l1
      Q[(ijn_to_idx[(i, j1, n1)], ijn_to_idx[(i, j1, n1)])] -= 2 * n1 * S * l1

# 各列の総和をSに制限
for j in range(1, N + 1):
  for i1 in range(1, N + 1):
    for n1 in range(1, N ** 2 + 1):
      for i2 in range(1, N + 1):
        for n2 in range(1, N ** 2 + 1):
          Q[(ijn_to_idx[(i1, j, n1)], ijn_to_idx[(i2, j, n2)])] += n1 * n2 * l1
      Q[(ijn_to_idx[(i1, j, n1)], ijn_to_idx[(i1, j, n1)])] -= 2 * n1 * S * l1

# 斜め(右下がり)の総和をSに制限
for d1 in range(1, N + 1):
  for n1 in range(1, N ** 2 + 1):
    for d2 in range(1, N + 1):
      for n2 in range(1, N ** 2 + 1):
        Q[(ijn_to_idx[(d1, d1, n1)], ijn_to_idx[(d2, d2, n2)])] += n1 * n2 * l1
    Q[(ijn_to_idx[(d1, d1, n1)], ijn_to_idx[(d1, d1, n1)])] -= 2 * n1 * S * l1
    
# 斜め(右上がり)の総和をSに制限
for d1 in range(1, N + 1):
  for n1 in range(1, N ** 2 + 1):
    for d2 in range(1, N + 1):
      for n2 in range(1, N ** 2 + 1):
        Q[(ijn_to_idx[(d1, N - d1 + 1, n1)], ijn_to_idx[(d2, N - d2 + 1, n2)])] += n1 * n2 * l1
    Q[(ijn_to_idx[(d1, N - d1 + 1, n1)], ijn_to_idx[(d1, N - d1 + 1, n1)])] -= 2 * n1 * S * l1

$f_0(\bm{x}) = \sum_{k}\sum_{l}\left(\sum_{(i, j) \in L_k}\sum_{n} nx_{i,j,n} - \sum_{(i, j) \in L_l}\sum_{n} nx_{i,j,n}\right)^2$ を使う場合は以下のような実装になります。
この場合は、 $\lambda_1 = 1, \lambda_2 = 100, \lambda_3 = 100$ くらいに設定するといい結果を出しやすいです。

# 各列に含まれるマスの集合を記録
L = []
# 横の行を記録
for i in range(1, N + 1):
  l = []
  for j in range(1, N + 1):
    l.append((i, j))
  L.append(l)
# 縦の列を記録
for j in range(1, N + 1):
  l = []
  for i in range(1, N + 1):
    l.append((i, j))
  L.append(l)
# 斜め(右下がり)の列を記録
l = []
for d in range(1, N + 1):
  l.append((d, d))
L.append(l)
# 斜め(右上がり)の列を記録
l = []
for d in range(1, N + 1):
  l.append((d, N - d + 1))
L.append(l)



# 各列の総和は等しくなるように制限
for L_k in L:
  for L_l in L:
    for i1, j1 in L_k:
      for i2, j2 in L_k:
        for n1 in range(1, N ** 2 + 1):
          for n2 in range(1, N ** 2 + 1):
            Q[(ijn_to_idx[(i1, j1, n1)], ijn_to_idx[(i2, j2, n2)])] += n1 * n2 * l1

    for i1, j1 in L_k:
      for i2, j2 in L_l:
        for n1 in range(1, N ** 2 + 1):
          for n2 in range(1, N ** 2 + 1):
            Q[(ijn_to_idx[(i1, j1, n1)], ijn_to_idx[(i2, j2, n2)])] -= 2 * n1 * n2 * l1

    for i1, j1 in L_l:
      for i2, j2 in L_l:
        for n1 in range(1, N ** 2 + 1):
          for n2 in range(1, N ** 2 + 1):
            Q[(ijn_to_idx[(i1, j1, n1)], ijn_to_idx[(i2, j2, n2)])] += n1 * n2 * l1

2. $1 \sim N^2$ はちょうど1回しか使えない

以下のコードは、 $f_4(\bm{x}) = \sum_{n}\left(\sum_{i}\sum_{j} x_{i,j,n} - 1\right)^2$ に対応しています。

# 同じ数字が重複しないように制限
for n in range(1, N ** 2 + 1):
  for i1 in range(1, N + 1):
    for j1 in range(1, N + 1):
      for i2 in range(1, N + 1):
        for j2 in range(1, N + 1):
          Q[(ijn_to_idx[(i1, j1, n)], ijn_to_idx[(i2, j2, n)])] += 1 * l2
      Q[(ijn_to_idx[(i1, j1, n)], ijn_to_idx[(i1, j1, n)])] -= 2 * l2

3.各マスに1つしか数字を入れてはいけない

以下のコードは、 $f_5(\bm{x}) = \sum_{i}\sum_{j}\left(\sum_{n} x_{i,j,n} - 1\right)^2$ に対応しています。

# 各マスにちょうど1つの数字に制限
for i in range(1, N + 1):
  for j in range(1, N + 1):
    for n1 in range(1, N ** 2 + 1):
      for n2 in range(1, N ** 2 + 1):
        Q[(ijn_to_idx[(i, j, n1)], ijn_to_idx[(i, j, n2)])] += 1 * l3
      Q[(ijn_to_idx[(i, j, n1)], ijn_to_idx[(i, j, n1)])] -= 2 * l3

量子アニーリングの実行

以下のコードは、solver(今回はAdvantage_system6.4)という量子アニーリングマシンで、QUBO行列 $Q$ に基づいて、num_reads(今回は1000)回量子アニーリングを実行しています。

# 量子アニーリングの実行
endpoint = 'https://cloud.dwavesys.com/sapi/'
dw_sampler = DWaveSampler(solver=solver, token=token, endpoint=endpoint)
sampler = EmbeddingComposite(dw_sampler)
sampleset = sampler.sample_qubo(Q, num_reads=num_reads)

2025年1月22日からD-Wave Leapの無料トライアルが使えなくなってしまったので、無料で使える最適化ライブラリでの実装方法も紹介しておきます。

最適化ライブラリとしてOpenJijを使うためにopenjijをインストールします。

pip install openjij

プログラムの方は、openjijからSASamplerをインポートし、量子アニーリングの実行部分を以下のように書き換えるだけで実行することができます。

from openjij import SASampler

# 焼きなまし法の実行
sampler = SASampler()
sampleset = sampler.sample_qubo(Q, num_reads=num_reads)

魔方陣の可視化

以下のコードは、num_reads回のアニーリングの中で最も上手くいった結果に基づいて魔方陣を生成し、それを可視化しています。

# 結果に基づいて魔方陣を生成
result = [i for i in sampleset.first[0].values()]
ans = [[None] * N for _ in range(N)]
for i in range(1, N + 1):
  for j in range(1, N + 1):
    for n in range(1, N ** 2 + 1):
      if result[ijn_to_idx[(i, j, n)]] == 1:
        ans[i - 1][j - 1] = n

# 魔方陣の表示
print(*ans, sep='\n')

結果

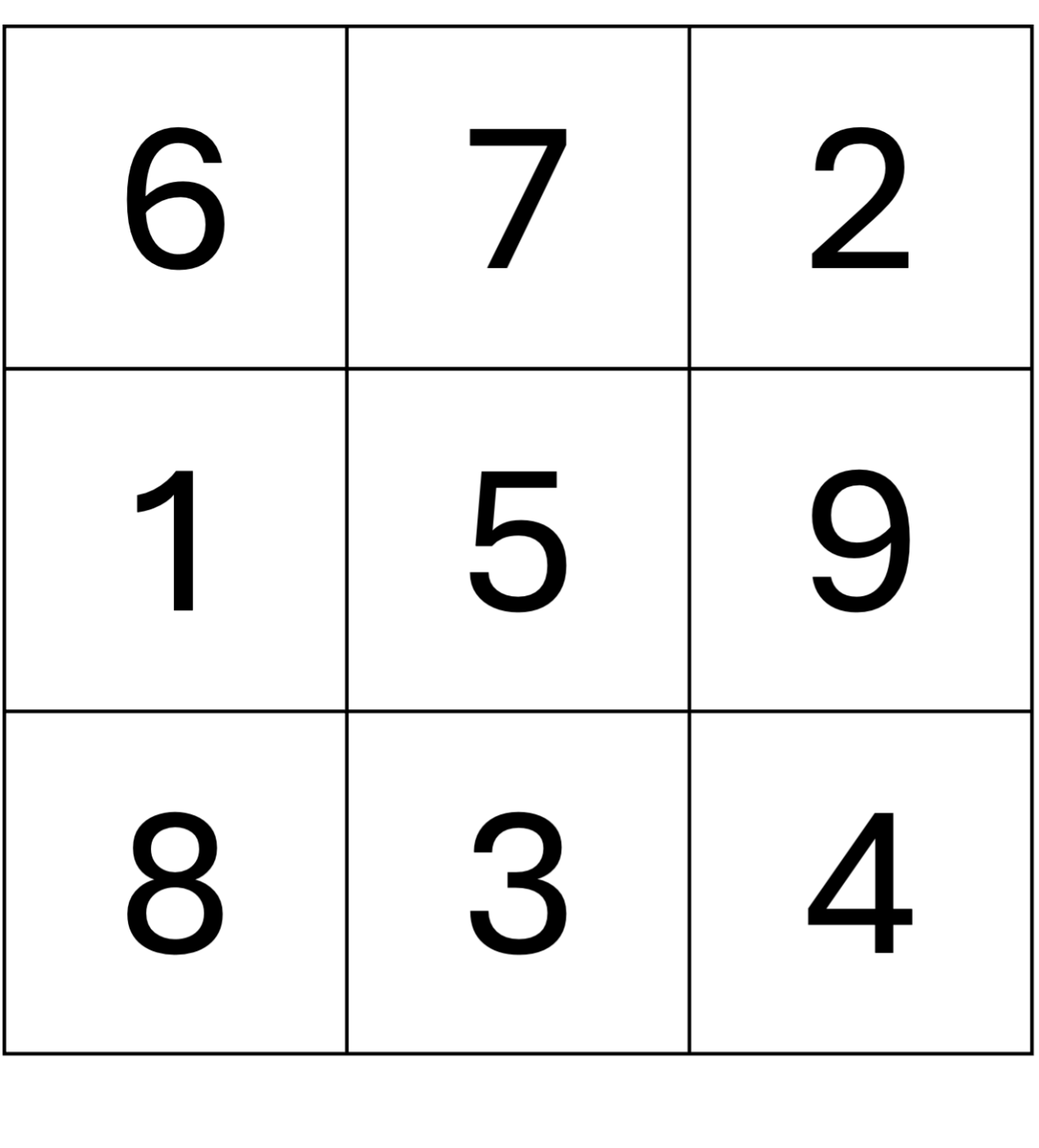
上のコードを実行すると以下のような出力が得られました。

[6, 7, 2]
[1, 5, 9]
[8, 3, 4]

これをきれいにすると以下のような魔方陣になり、この記事の最初の方で紹介した $3 \times 3$ の魔方陣を右に90°回転したものと一致していることがわかります。

まとめ

この記事では、量子アニーリングを用いて魔方陣を生成する方法について解説しました。
今回作成した最適化問題はかなり不安定で $3 \times 3$ の場合でも間違った結果をたびたび出してしまいました。 $4 \times 4$ などさらに大きな問題の場合はより不安定になってしまうため、罰金項の強さを適切に調整しないといけませんでした。安定する罰金項の値を見つけた方や簡単に決定できるアルゴリズムを見つけた方は共有いただけると幸いです。

脚注

組合せ最適化問題とは、多くの選択肢からある制約をもとに最も良い解を求める問題のこと。ナップサック問題やSAT問題などが挙げられる。 ↩︎

GitHubで編集を提案

はじめに

量子アニーリングとは

魔方陣

量子アニーリングで魔方陣を解いてみる

定式化

1.各列の総和は等しい

1-1.横の行の総和はS

1-2.縦の列の総和はS

1-3.斜めの列の総和はS

2.1 \sim N^2はちょうど1回しか使えない

3.各マスに1つしか数字を入れてはいけない

魔方陣生成の評価関数

実装

初期化

QUBO行列Qの設定

1.各列の総和は等しい

2.1 \sim N^2はちょうど1回しか使えない

3.各マスに1つしか数字を入れてはいけない

量子アニーリングの実行

魔方陣の可視化

結果

まとめ

Discussion

1-1.横の行の総和は $S$

1-2.縦の列の総和は $S$

1-3.斜めの列の総和は $S$

2. $1 \sim N^2$ はちょうど1回しか使えない

QUBO行列 $Q$ の設定

2. $1 \sim N^2$ はちょうど1回しか使えない