データ分析 主成分分析2
前回の データ分析 主成分分析1に続き、もう少し実践的なデータで主成分分析を行ってみます。
関連する記事
データ分析 主成分分析1
データ分析 python 基本のグラフ -散布図-
前準備
必要なライブラリを読み込んでおきます
!pip install -q japanize_matplotlib
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns
import numpy as np
from sklearn.preprocessing import StandardScaler # 標準化で使用
from sklearn.decomposition import PCA # 主成分分析で使用
plt.style.use('seaborn')
plt.rcParams['font.family'] = 'IPAexGothic'
データを読み込んでおきます
df_org = pd.read_csv('/content/drive/MyDrive/jewelry_shop_reviews.csv')
df_org.head(3)

主成分分析に不要な変数を削除
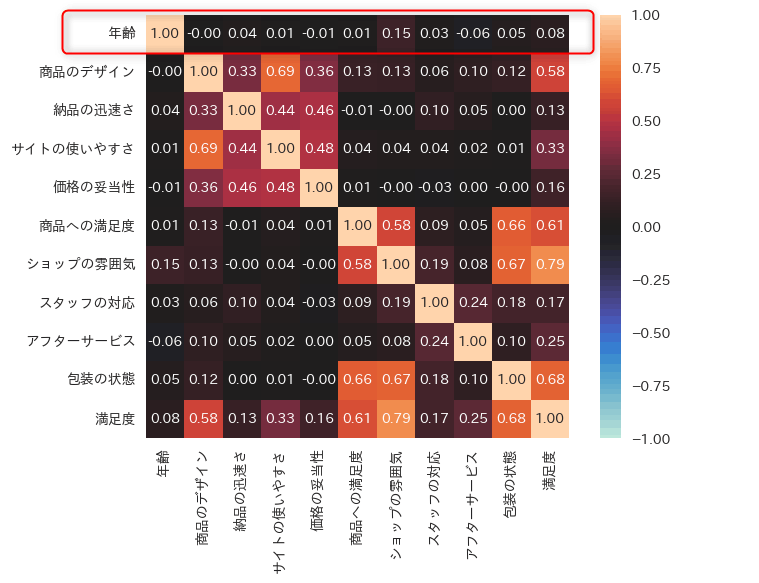
まずデータの相関係数をヒートマップで確認します。
sns.heatmap(df_org.corr(numeric_only=True), annot=True, square=True, vmax=1, vmin=-1, center=0, fmt='.2f')
年齢がどの項目ともほぼ相関がありません。
主成分分析に不要な変数を除外しておきます。
- どの項目とも相関がない変数
- 目的変数、
- カテゴリカル変数
df=df_org.drop(['満足度','年齢'], axis=1).select_dtypes(include='number')
df.head(3)

変数の標準化
主成分分析ではデータのスケールを統一しておく必要があり、なおかつデータの平均を0にしておく必要があるので、変数の標準化を行います。
scaler = StandardScaler()
scaled = scaler.fit_transform(df)
scaled

主成分分析を行う
PCAクラスをインスタンス化する際にrandom_state=0を指定して、同じデータと同じ設定で実行したときは、同じ結果が得られるように乱数を固定します。
pca = PCA(random_state=0)
pca_res = pca.fit_transform(scaled)
pca_res

主成分分析の結果の解析 1.寄与率を確認
寄与率が高い主成分ほどデータのばらつきを多く説明しているため、重要度が高い主成分として認識されます。
ratio=pca.explained_variance_ratio_
ratio

見ずらいのでDataFrameに変換します
df_ratio = pd.DataFrame(ratio, columns=['寄与率'], index=[f'PC{x+1}' for x in range(len(ratio))] )
df_ratio
一般的には、第四主成分までで70~80%の累積寄与率が得られれば、主成分分析としては良好な結果とされています。

第四主成分までの累積寄与率は75%ほどなので問題なさそうです
sum(ratio[:4])
# => 0.7499509364983603
主成分分析の結果の解析 2.主成分負荷量を確認
主成分負荷量は、主成分が元の変数に対してどれだけ強く影響を与えているかを示す指標です。
主成分負荷量を見ることで、どの元の変数が各主成分に強く影響しているかがわかります。
主成分負荷量は、固有ベクトル × 固有値の平方根 で算出します。
まずは固有ベクトルを取得します。
components = pca.components_
components.shape
# => (9, 9)
次に固有値を取得し、その平方根を求めます
# 固有値を取得する
eigenvalues = pca.explained_variance_
# 固有値の平方根を算出
eigenvalues_sqrt = np.sqrt(eigenvalues)
eigenvalues_sqrt.shape
# => (9,)
固有ベクトルとの乗算するため、固有値の平方根をリシェイプします
re_eigenvalues_sqrt = eigenvalues_sqrt.reshape(9,1)
re_eigenvalues_sqrt.shape
主成分負荷量を計算します。
# 主成分負荷量 = 固有ベクトル × 固有値の平方根
loadings = components * re_eigenvalues_sqrt
loadings
主成分負荷量をデータフレームに変換しておきます
df_loadings = pd.DataFrame(loadings, columns=df.columns, index=[f'PC{x+1}' for x in range(loadings.shape[1])])
df_loadings

主成分分析の結果の解析 3.可視化して確認する
ヒートマップで相関関係を確認する
第三主成分までをヒートマップで相関関係を確認してみます
sns.heatmap(df_loadings.head(3), annot=True, square=True, vmax=1, vmin=-1, center=0, fmt='.2f')

- 第一主成分
- すべての項目に対する評価と解釈できそう
- スタッフの対応、アフターサービスは全体への影響は少なそう
- 第二主成分
- 正の相関:商品のデザイン、納品の迅速さ、サイトの使いやすさ、価格の妥当性
- 負の相関:商品の満足度、ショップの雰囲気、包装の状態
- 正の相関は購入決定に関するもの、負の相関は購入前後の体験に関するものと解釈できそうです
- 第三主成分
- 第一主成分で負荷量が小さかった、 スタッフの対応、アフターサービスの絶対値が大きい
- 従業員の評価と解釈できそう
主成分軸を散布図で確認
第一主成分軸と第二主成分軸を散布図で可視化してみます。
pc1 = components[0]
pc2 = components[1]
for x, y, label in zip(pc1, pc2, df.columns):
plt.text(x, y, label)
plt.scatter(pc1, pc2)
plt.xlabel('PC1')
plt.ylabel('PC2')

主成分軸をプロットするメソッドを作成しておくと、いろいろな組み合わせで主成分軸を可視化できて便利です
# 主成分軸を散布図でプロットするメソッド
def plot_components(x, y):
pcX = components[x-1]
pcY = components[y-1]
for _x, _y, label in zip(pcX, pcY, df.columns):
plt.text(_x, _y, label)
plt.scatter(pcX, pcY)
plt.xlabel(f'PC{x}')
plt.ylabel(f'PC{y}')
# 第一主成分軸と第二主成分軸を散布図でプロット
plot_components(1, 2)
主成分得点を散布図で確認
第一主成分得点と第二主成分得点を散布図で可視化し、満足度に応じて色付けしてみます。
# 第一主成分得点と第二主成分得点を散布図で可視化する
pc1 = pca_res[:,0] # すべての行の0列目
pc2 = pca_res[:,1] # すべての行の1列目
no = range(len(pca_res))
# 散布図をプロット
plt.scatter(pc1, pc2, alpha=0.8, c=list(df_org['満足度']), cmap='viridis')
plt.xlabel('PC1')
plt.ylabel('PC2')

満足度が高い人は少し左下に集まっているようですので、満足度が高い人は購入前後の体験に高い評価点を付けているのかもしれません。
また、満足度が低い人は少し右上に集まっているようですので、満足度が低い人は購入決定に関するものに高い評価点を付けているのかもしれません。
主成分得点を散布図でプロットするメソッドを作成しておくと、便利です。
# 主成分得点を散布図でプロットするメソッド
def plot_pca_result(x, y):
pcX = pca_res[:,x-1] # すべての行の0列目
pcY = pca_res[:,y-1] # すべての行の1列目
plt.scatter(pcX, pcY, alpha=0.8, c=list(df_org['満足度']), cmap='viridis')
plt.xlabel(f'PC{x}')
plt.ylabel(f'PC{y}')
第ニ主成分得点と第三主成分得点を散布図で可視化してみます。
plot_pca_result(1, 3)
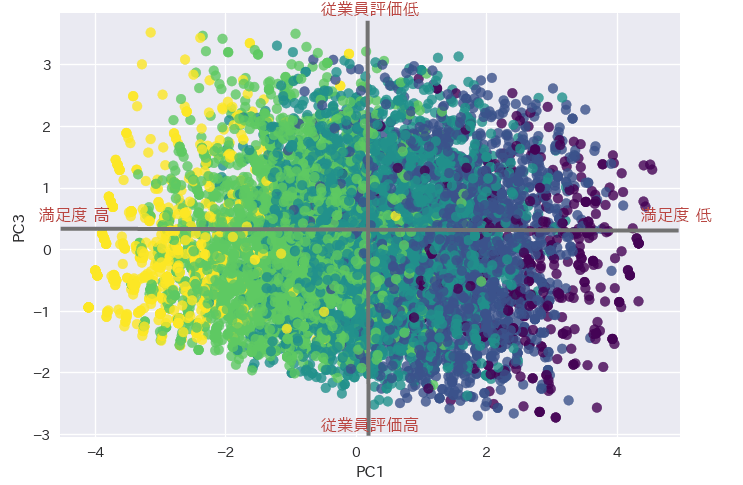
従業員の評価はあまり満足度には影響していないようです。
3Dで可視化すると、何かほかに読み取れることがあるかもしれません。
from mpl_toolkits.mplot3d import Axes3D #3D表示で使用
pc1 = pca_res[:,0] # すべての行の0列目
pc2 = pca_res[:,1] # すべての行の1列目
pc3 = pca_res[:,2] # すべての行の2列目
fig = plt.figure(figsize=(8,8))
ax = fig.add_subplot(111, projection='3d')
sc = ax.scatter(pc1, pc2, pc3, alpha=0.8, c=list(df_org['満足度']), cmap='viridis')
ax.set_xlabel('PC1')
ax.set_ylabel('PC2')
ax.set_zlabel('PC3')
fig.colorbar(sc)
plt.tight_layout()

主成分得点の散布図の上に主成分負荷量を矢印で視覚化することで、各変数がデータの分布にどのように影響しているかを一目で理解しやすくなります。
import matplotlib.patches as patches
# 主成分得点プロット
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(111)
plt.title(f'第1, 第2主成分得点のプロット')
plt.scatter(pca_res[:, 0], pca_res[:, 1], alpha=0.8, c=list(df.iloc[:, -1]), cmap='viridis')
plt.xlabel(f'PC1')
plt.ylabel(f'PC2')
# 主成分負荷量を図示
pc1 = loadings[0] # 第一主成分の主成分負荷量
pc2 = loadings[1] # 第二主成分の主成分負荷量
arrow_magnification = 3 # 矢印の倍率
feature_names = df.columns.to_list() # カラム名の取得
# ガイド円
patch_circle = patches.Circle(
xy=(0, 0), # ガイド円の中心の設定
radius=1 * arrow_magnification, # 半径の設定
ec='darkred', # 円の色
fill=False # 円内の塗りつぶし
)
# ガイド円をグラフ上に追加
ax.add_patch(patch_circle)
# 矢印と変数ラベルの追加
for i in range(len(feature_names)):
# 矢印の表示と設定
ax.arrow(0, 0, # 矢印の中心の設定
pc1[i] * arrow_magnification, # 矢印の長さの設定
pc2[i] * arrow_magnification, # 矢印の長さの設定
head_width=0.1, # 矢印の頭の設定
head_length=0.1, # 矢印の頭の設定
color='darkred' # 矢印の色
)
# 変数ラベル
ax.text(pc1[i] * arrow_magnification * 1.2,
pc2[i] * arrow_magnification * 1.2,
feature_names[i])
plt.axis('equal')
plt.show()

箱ひげ図で可視化
箱ひげ図でも可視化していみます。
第一主成分、第二主成分、第三主成分を取り出します。
df_pca_sub = df_pca.iloc[:, 0:3]
df_pca_sub.columns = ['総合評価', '購入体験評価', '従業員評価']
df_pca_sub

元のデータの満足度と結合し、新しいDataFrameを作成します
df_new = pd.concat([df_org['満足度'], df_pca_sub], axis=1)
df_new.head()

満足度と第一主成分(総合評価)を箱ひげ図で表示してみます
plt.figure(figsize=(8, 6))
plt.title('満足度と総合評価')
sns.boxplot(x='満足度', y='総合評価', data=df_new, hue='満足度', palette='colorblind')
総合評価と満足度は連動していることが確認できます。

満足度と第二主成分(購入体験評価)を箱ひげ図で表示してみます
plt.figure(figsize=(8, 6))
plt.title('満足度と購入体験評価')
sns.boxplot(x='満足度', y='購入体験評価', data=df_new, hue='満足度', palette='colorblind')
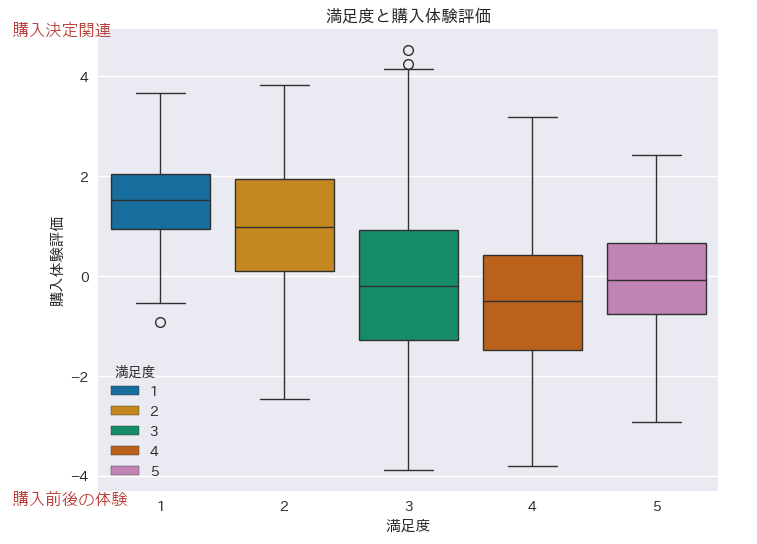
満足度1,2を付けた人は購入決定時の体験(商品のデザイン、納品の迅速さ、サイトの使いやすさ、価格の妥当性)に高評価を付けているようです。
満足度3,4を付けた人は購入前後の体験(商品の満足度、ショップの雰囲気、包装の状態)に高評価を付けたようです。
plt.figure(figsize=(8, 6))
plt.title('満足度と従業員評価')
sns.boxplot(x='満足度', y='従業員評価', data=df_new, hue='満足度', palette='colorblind')

従業員の評価はあまり満足度に影響していないようです。
まとめ
今回の分析からは、購入前後の体験(商品の満足度、ショップの雰囲気、包装の状態)などが満足度に影響を与えているのではないかと解析できるのではないでしょうか。
以上、主成分分析と結果の解析方法についてでした。
Discussion