データ分析 主成分分析1
今回は主成分分析の基礎についてまとめてみます。
主成分分析とは
主成分分析は次元削減に用いられる多変量解析の手法の 1 つです。
データに含まれる多くの次元(列)を、できるだけ元のデータの情報を失わないように新しい軸を作り直して次元を縮小する方法です。
これにより、データのばらつきや重要な特徴を少ない次元で表現でき、データの処理や解釈が容易になります。
簡単に言えば、
データの中で最もばらつきが大きい方向(分散が最大の方向)に軸をとり、それをx軸に代わる新しい軸(第一主成分軸)とします。
次に、ばらつきが次に大きい方向に軸をとり(第一主成分軸に直交する方向になる)y軸に代わる新しい軸(第二主成分軸)とします。
さらに、ばらつきが次に大きい方向に軸をとり(第一・第二主成分軸の両方に直交する方向になります)z軸に代わる新しい軸(第三主成分軸)とし、このように次元を削減していきます。
こうして、ばらつきが大きい方向に軸をとっていくことで、元のデータから失われる情報を最小限に抑えながら次元数を減らしていきます。
- バラバラなデータから、データのばらつきが最も大きい方向を見つけます。
- 最もばらつきが大きい方向に軸をとり、失われる情報を最小限に抑えます。
- データは最もばらつきが大きい方向(第一主成分軸)に沿って並び、元の情報を可能な限り保持したまま、次元を1つに減らすことができます。(x軸、y軸 → 第一主成分軸)

主成分分析で出てくる用語
主成分分析ではいろいろなワードが出てきて混乱しますので、簡単にイメージを押さえておきます。
主成分
次元削減に用いる新しい軸のことです。
主成分得点
元のデータをその新しい軸に投影した後の値のことです。
固有ベクトル
主成分の方向を示すベクトルのことです。
データの中で最もばらつきが大きい方向を表します。
固有ベクトルと主成分軸は、基本的に同じものを指します。
固有ベクトルが主成分軸の方向を示し、その軸に沿ってデータを再構成します。
固有値
固有ベクトル(主成分軸)に沿ったデータの分散の大きさを表します。
それぞれの主成分が、元のデータのばらつきをどれだけ説明しているかを示す指標でう。
固有値が大きい主成分ほど、データの重要な特徴をよく捉えているといえます。
具体的には、固有値が大きいほど、その主成分軸に沿ってデータの分散(情報量)が多いことを示します。
主成分負荷量
主成分負荷量は、主成分が元の変数に対してどれだけ強く影響を与えているかを示す指標です。
主成分負荷量は、固有ベクトルに固有値の平方根を掛けたものとして定義されます。
符号は元の変数と主成分の関連性の方向(正または負)を示し、数値の絶対値はその関連の強さを示します。
主成分負荷量を見ることで、どの元の変数が各主成分に強く影響しているかがわかります。
寄与率
各主成分の固有値を全ての固有値の合計で割ることで、その主成分が全体のデータに対してどれだけ寄与しているか(データのばらつきをどれだけ説明しているか)を示す割合のことです。
寄与率が高い主成分ほどデータのばらつきを多く説明しているため、重要度が高い主成分として認識されます。
主成分分析を行う
使用したデータ
主成分分析でよく使用される学生の成績データです。
使用したデータ
| 現代文 | 古文 | 数学 | 化学 | 生物 | 物理 | 歴史 | 世界史 | 政治経済 | 英語 |
|---|---|---|---|---|---|---|---|---|---|
| 3.0 | 4.5 | 6.0 | 4.5 | 4.5 | 6.0 | 4.5 | 3.0 | 4.5 | 3.0 |
| 7.5 | 6.0 | 4.5 | 4.5 | 4.5 | 3.0 | 6.0 | 4.5 | 6.0 | 7.5 |
| 4.5 | 4.5 | 4.5 | 6.0 | 4.5 | 6.0 | 4.5 | 6.0 | 6.0 | 4.5 |
| 7.5 | 7.5 | 4.5 | 4.5 | 4.5 | 4.5 | 6.0 | 6.0 | 6.0 | 7.5 |
| 6.0 | 4.5 | 6.0 | 7.5 | 6.0 | 4.5 | 4.5 | 4.5 | 6.0 | 4.5 |
| 4.5 | 4.5 | 4.5 | 4.5 | 4.5 | 4.5 | 6.0 | 4.5 | 6.0 | 4.5 |
| 4.5 | 6.0 | 4.5 | 6.0 | 6.0 | 6.0 | 4.5 | 4.5 | 6.0 | 6.0 |
| 7.5 | 7.5 | 6.0 | 7.5 | 7.5 | 7.5 | 6.0 | 7.5 | 7.5 | 7.5 |
| 3.0 | 3.0 | 1.5 | 3.0 | 1.5 | 1.5 | 3.0 | 4.5 | 4.5 | 1.5 |
| 4.5 | 4.5 | 7.5 | 6.0 | 7.5 | 7.5 | 4.5 | 4.5 | 4.5 | 7.5 |
| 4.5 | 4.5 | 7.5 | 4.5 | 4.5 | 7.5 | 4.5 | 4.5 | 3.0 | 3.0 |
| 7.5 | 7.5 | 3.0 | 4.5 | 4.5 | 3.0 | 4.5 | 4.5 | 4.5 | 7.5 |
| 4.5 | 4.5 | 4.5 | 6.0 | 4.5 | 4.5 | 4.5 | 6.0 | 4.5 | 4.5 |
| 4.5 | 3.0 | 3.0 | 4.5 | 4.5 | 3.0 | 4.5 | 4.5 | 4.5 | 6.0 |
| 7.5 | 7.5 | 7.5 | 7.5 | 7.5 | 7.5 | 7.5 | 7.5 | 7.5 | 7.5 |
| 4.5 | 1.5 | 3.0 | 1.5 | 3.0 | 1.5 | 4.5 | 4.5 | 4.5 | 3.0 |
| 4.5 | 6.0 | 4.5 | 4.5 | 4.5 | 4.5 | 7.5 | 7.5 | 7.5 | 7.5 |
| 6.0 | 6.0 | 4.5 | 4.5 | 4.5 | 4.5 | 6.0 | 4.5 | 6.0 | 7.5 |
| 6.0 | 6.0 | 7.5 | 7.5 | 7.5 | 7.5 | 4.5 | 6.0 | 4.5 | 3.0 |
| 7.5 | 7.5 | 3.0 | 3.0 | 3.0 | 3.0 | 4.5 | 4.5 | 4.5 | 7.5 |
| 4.5 | 4.5 | 7.5 | 6.0 | 7.5 | 7.5 | 4.5 | 4.5 | 6.0 | 4.5 |
| 1.5 | 1.5 | 7.5 | 7.5 | 4.5 | 7.5 | 3.0 | 3.0 | 1.5 | 1.5 |
| 7.5 | 4.5 | 3.0 | 3.0 | 4.5 | 1.5 | 7.5 | 7.5 | 6.0 | 4.5 |
| 7.5 | 7.5 | 7.5 | 6.0 | 7.5 | 6.0 | 7.5 | 7.5 | 7.5 | 6.0 |
| 4.5 | 4.5 | 4.5 | 6.0 | 4.5 | 4.5 | 4.5 | 6.0 | 4.5 | 4.5 |
| 4.5 | 7.5 | 4.5 | 4.5 | 4.5 | 4.5 | 4.5 | 6.0 | 4.5 | 7.5 |
| 3.0 | 4.5 | 3.0 | 4.5 | 4.5 | 3.0 | 7.5 | 7.5 | 7.5 | 4.5 |
| 4.5 | 4.5 | 6.0 | 4.5 | 4.5 | 6.0 | 4.5 | 4.5 | 4.5 | 6.0 |
| 1.5 | 1.5 | 3.0 | 1.5 | 1.5 | 1.5 | 3.0 | 1.5 | 3.0 | 1.5 |
| 7.5 | 7.5 | 7.5 | 7.5 | 7.5 | 7.5 | 7.5 | 7.5 | 7.5 | 7.5 |
| 4.5 | 4.5 | 6.0 | 6.0 | 6.0 | 6.0 | 4.5 | 3.0 | 4.5 | 6.0 |
| 4.5 | 4.5 | 4.5 | 4.5 | 4.5 | 4.5 | 4.5 | 4.5 | 4.5 | 4.5 |
| 7.5 | 7.5 | 7.5 | 7.5 | 6.0 | 7.5 | 4.5 | 4.5 | 4.5 | 7.5 |
| 6.0 | 4.5 | 6.0 | 6.0 | 6.0 | 6.0 | 6.0 | 4.5 | 6.0 | 4.5 |
| 6.0 | 4.5 | 3.0 | 4.5 | 4.5 | 3.0 | 4.5 | 6.0 | 4.5 | 7.5 |
| 4.5 | 4.5 | 4.5 | 4.5 | 4.5 | 4.5 | 7.5 | 7.5 | 7.5 | 4.5 |
| 4.5 | 4.5 | 7.5 | 4.5 | 6.0 | 6.0 | 4.5 | 4.5 | 4.5 | 3.0 |
| 4.5 | 4.5 | 6.0 | 4.5 | 4.5 | 6.0 | 6.0 | 6.0 | 7.5 | 4.5 |
| 7.5 | 7.5 | 6.0 | 6.0 | 7.5 | 6.0 | 7.5 | 7.5 | 7.5 | 7.5 |
| 1.5 | 3.0 | 1.5 | 1.5 | 1.5 | 3.0 | 1.5 | 1.5 | 1.5 | 3.0 |
以下略
主成分分析
前準備
必要なライブラリとデータを読み込んでおきます
!pip install -q japanize_matplotlib # 日本語対応
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns
plt.style.use('seaborn')
plt.rcParams['font.family'] = 'IPAexGothic'
# データ読込
df = pd.read_csv('/content/drive/MyDrive/student report.csv')
df.head(3)

相関関係を確認
ヒートマップで相関関係を確認します。
主成分分析では、どの項目とも無相関の変数はあらかじめ取り除いておくのですが
今回はどの項目も何かしらの相関があります。
sns.heatmap(df.corr(), annot=True, vmax=1, vmin=-1, center=0, square=True, fmt='.2f')

変数を標準化
主成分分析ではデータのスケールを統一しておく必要があり、なおかつデータの平均を0にしておく必要があるので、特別な理由がない限り変数の標準化を行います。
StandardScalerクラス の fit_transform メソッド で 標準化を行い、平均を0、標準偏差を1にします。
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler() # インスタンス化
scaled = scaler.fit_transform(df) # 標準化
主成分分析を行う
主成分分析は sklearn の PCA クラスを使用します。
PCAをインスタンス化する際にrandom_state=0を指定して
同じデータと同じ設定で実行したときは、同じ結果が得られるように乱数を固定します。
from sklearn.decomposition import PCA
pca = PCA(random_state=0) # インスタンス化
pca = pca.fit_transform(scaled) # 主成分分析
主成分分析の結果を解析
主成分分析の結果を確認してみます。
40行10列 の numpy.ndarray 型 になっています。
print(pca_result.shape) #=> (40, 10)
print(type(pca_result))
pca_result

numpy.ndarray 型では見づらいので、DataFrame 型に変換します。
# 主成分分析の結果が numpy.ndarray で見難いので DataFrameに変換
df_pca_result = pd.DataFrame(pca_result,
columns=[ f'PC{i+1}' for i in range(pca_result.shape[1]) ])
df_pca_result.head(5)
PC1が第一主成分、PC2が第二主成分、・・・・となり、一つ一つの値を主成分得点とよびます。

寄与率を確認する
寄与率とは各主成分の固有値を全ての固有値の合計で割ることで、その主成分が全体のデータに対してどれだけ寄与しているか(データのばらつきをどれだけ説明しているか)を示す割合のことです。
寄与率が高い主成分ほどデータのばらつきを多く説明しているため、重要度が高い主成分として認識されます。
寄与率は pcaインスタンスの explained_variance_ratio_ プロパティで取得できます
ratio = pca.explained_variance_ratio_
print(type(ratio))
ratio

numpy.ndarray型だと見づらいので dataFrame型にします。
df_ratio = pd.DataFrame(ratio,
columns=['寄与率'],
index=[ f'PC{i+1}' for i in range(len(ratio))] )
df_ratio
第一主成分、第二主成分、第三主成分 で 元のデータの大部分を表現できています。

第一主成分から第三主成分までを加算した累積寄与率は約87%で、これはもとのデータの87%の情報を保持していると考えられます。
累積寄与率が 70%~80% に達していれば、元のデータの大部分の情報を保持していると考えられます。
主成分分析 (PCA) では、累積寄与率が 70%~80% 程度になるように主成分を選ぶことが一般的な目安とされています。
sum(ratio[:3])
# => 0.877917・・・
主成分負荷量を確認する
主成分負荷量は、主成分が元の変数に対してどれだけ強く影響を与えているかを示す指標です。
主成分負荷量は、固有ベクトルに固有値の平方根を掛けたものとして定義されます。
符号は元の変数と主成分の関連性の方向(正または負)を示し、数値の絶対値はその関連の強さを示します。
主成分負荷量を見ることで、どの元の変数が各主成分に強く影響しているかがわかります。
主成分負荷量を算出します。
主成分負荷量は、固有ベクトル × 固有値の平方根 で算出します。
まずは固有ベクトルを取得します。
componets = pca.components_
print(type(componets))
componets.shape

固有値を取得し、平方根を算出します。
# 固有値を取得
eigenvalues = pca.explained_variance_
# 固有値の平方根を算出
eigenvalues_sqrt = np.sqrt(eigenvalues)
print(type(eigenvalues))
eigenvalues_sqrt.shape

固有値の平方根は 長さ 10 の 1次元配列です。
行列の乗算では、掛けられる行列の列数と、掛ける行列の行数を一致させる必要があります。
ここで掛けられる行列とは固有ベクトル、掛ける行列は固有値の平方根です。
乗算ができるように固有値の平方根を10行1列の行列に変換します。
re_eigenvalues_sqrt = eigenvalues_sqrt.reshape(10,1)
print(type(re_eigenvalues_sqrt))
re_eigenvalues_sqrt.shape

では 主成分負荷量を計算します。
loadings = componets * re_eigenvalues_sqrt
print(type(loadings))
print(loadings.shape)
loadings

numpy.ndarray型だと見づらいので dataFrame型にします。
df_loadings = pd.DataFrame(loadings,
columns=df.columns,
index=[ f'PC{i+1}' for i in range(loadings.shape[1]) ])
df_loadings

主成分負荷量をヒートマップで確認
寄与率を確認した際、第一主成分、第二主成分、第三主成分 で 元のデータの大部分を表現できていましたので、第三主成分までの主成分負荷量をヒートマップで表示してみます。
sns.heatmap(df_loadings.head(3), annot=True, vmax=1, vmin=-1, center=0, square=True, fmt='.2f')

- PC1(第一主成分)の解釈
すべて負の値で数値に大きな違いはありません。
元の数値が高くなれば(つまり点数が良くなれば)主成分負荷量の絶対値も大きくなります。
第一主成分は、総合得点を表していると解釈できそうです。 - PC2(第二主成分)の解釈
正の相関:数学、化学、生物、物理
負の相関:現代文、古文、歴史、世界史、政治経済、英語
正の相関は理数系科目、負の相関は文系科目ということで、第二主成分は、理系/文系を表していると解釈できそうです。 - PC3(第三主成分)の解釈
正の相関:歴史、世界史、政治経済
負の相関:現代文、古文、英語
無相関:数学、化学、生物、物理
正の相関は歴史系科目、負の相関は言語系科目と解釈できそうです。
どのように解釈するかは、解析者に任せられています。
主成分軸を散布図で確認
主成分分析の結果得られた固有ベクトルから、第一主成分(PC1)軸と第二主成分(PC2)軸を使って、散布図を表示してみます。
# 第一主成分軸と第二主成分軸を散布図で可視化する
pc1 = componets[0]
pc2 = componets[1]
# 散布図にテキストを描画
for x, y, label in zip(pc1, pc2, df.columns):
plt.text(x, y, label)
# 散布図をプロット
plt.scatter(pc1, pc2, alpha=0.8)
plt.xlabel('PC1')
plt.ylabel('PC2')

つづいて
固有ベクトルから、第二主成分(PC2)軸と第三主成分(PC3)軸を使って、散布図を表示してみます。
# 第二主成分軸と第三主成分軸を散布図で可視化する
pc2 = componets[1]
pc3 = componets[2]
# 散布図にテキストを描画
for x, y, label in zip(pc2, pc3, df.columns):
plt.text(x, y, label)
# 散布図をプロット
plt.scatter(pc2, pc3, alpha=0.8)
plt.xlabel('PC2')
plt.ylabel('PC3')

主成分得点を散布図で確認
主成分分析の結果得られた主成分得点から、第一主成分得点と第二主成分得点を使って、散布図を表示してみます。
# 第一主成分得点と第二主成分得点を散布図で可視化する
pc1 = pca_result[:,0] # すべての行の0列目
pc2 = pca_result[:,1] # すべての行の1列目
no = range(len(pca_result))
# 散布図にテキストを描画
for x, y, label in zip(pc1, pc2, no):
plt.text(x, y, label)
# 散布図をプロット
plt.scatter(pc1, pc2, alpha=0.8)
plt.xlabel('PC1')
plt.ylabel('PC2')
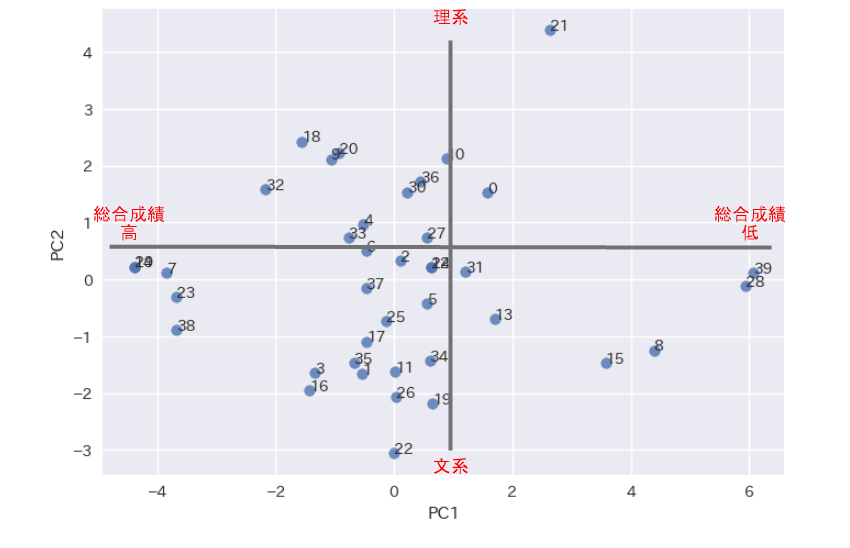
だいたい成績は中ほどで、理系文系に差はさほどないように見えます。
成績優秀者は文系が多いでしょうか。
つづいて第二主成分得点と第三主成分得点を使って、散布図を表示してみます。
# 第二主成分得点と第三主成分得点を散布図で可視化する
pc2 = pca_result[:,1] # すべての行の2列目
pc3 = pca_result[:,2] # すべての行の3列目
no = range(len(pca_result))
# 散布図にテキストを描画
for x, y, label in zip(pc2, pc3, no):
plt.text(x, y, label)
# 散布図をプロット
plt.scatter(pc2, pc3, alpha=0.8)
plt.xlabel('PC2')
plt.ylabel('PC3')

文系は歴史系と言語系の2グループに分かれているように見えます。
以上、主成分分析について簡単にまとめてみました。
Discussion