Open2
Rで行列計算をちゃんと勉強する
ピン留めされたアイテム
行列分解を理解する
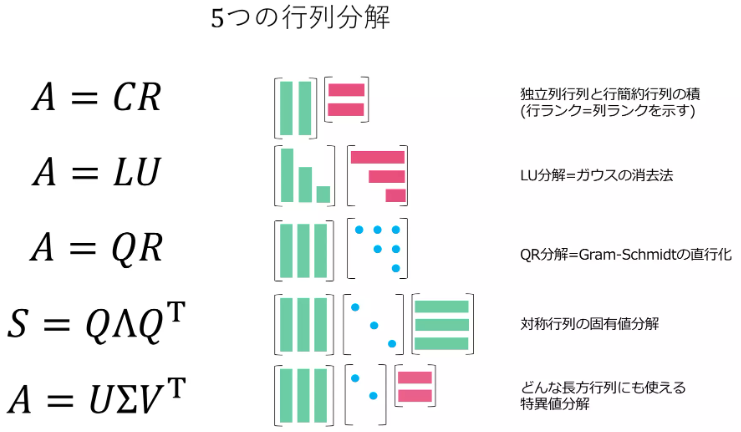
の5つに関して理解することを目標
参考)Gilbert Strang先生から学んだ線形代数 #math - Qiita
ToC
- 行ランク=列ランク
- LU分解
- QR分解
- 固有値の計算 https://zenn.dev/link/comments/8c14071af7607d
- 特異値分解
固有値の計算を理解する
eigen()
> eigen
function (x, symmetric, only.values = FALSE, EISPACK = FALSE)
{
x <- unname(as.matrix(x))
n <- nrow(x)
if (!n)
stop("0 x 0 matrix")
if (n != ncol(x))
stop("non-square matrix in 'eigen'")
n <- as.integer(n)
if (is.na(n))
stop("invalid nrow(x)")
complex.x <- is.complex(x)
if (!all(is.finite(x)))
stop("infinite or missing values in 'x'")
if (missing(symmetric))
symmetric <- isSymmetric.matrix(x)
if (symmetric) {
z <- if (!complex.x)
.Internal(La_rs(x, only.values))
else .Internal(La_rs_cmplx(x, only.values))
ord <- rev(seq_along(z$values))
}
else {
z <- if (!complex.x)
.Internal(La_rg(x, only.values))
else .Internal(La_rg_cmplx(x, only.values))
ord <- sort.list(Mod(z$values), decreasing = TRUE)
}
if (only.values)
list(values = z$values[ord], vectors = NULL)
else structure(class = "eigen", list(values = z$values[ord],
vectors = z$vectors[, ord, drop = FALSE]))
}
#> <bytecode: 0x000001a085335e78>
#> <environment: namespace:base>
のソースコードを見るに、計算自体は
.Internal(La_rg(x, only.values))でやってそうなので、r-srcを見てみると、下記で定義しているので、メモ
/* Real, general case of eigen */
static SEXP La_rg(SEXP x, SEXP only_values)
{
bool vectors, complexValues;
int i, n, lwork, info, *xdims, ov;
double *work, *wR, *wI, *left, *right, *xvals, tmp;
char jobVL[2] = "N", jobVR[2] = "N";
xdims = INTEGER(coerceVector(getAttrib(x, R_DimSymbol), INTSXP));
n = xdims[0];
if (n != xdims[1])
error(_("'x' must be a square numeric matrix"));
/* work on a copy of x */
if (!isReal(x)) {
x = coerceVector(x, REALSXP);
xvals = REAL(x);
} else {
xvals = (double *) R_alloc(n * (size_t)n, sizeof(double));
Memcpy(xvals, REAL(x), (size_t) n * n);
}
PROTECT(x);
ov = asLogical(only_values);
if (ov == NA_LOGICAL) error(_("invalid '%s' argument"), "only.values");
vectors = !ov;
left = right = (double *) 0;
if (vectors) {
jobVR[0] = 'V';
right = (double *) R_alloc(n * (size_t)n, sizeof(double));
}
wR = (double *) R_alloc(n, sizeof(double));
wI = (double *) R_alloc(n, sizeof(double));
/* ask for optimal size of work array */
lwork = -1;
F77_CALL(dgeev)(jobVL, jobVR, &n, xvals, &n, wR, wI,
left, &n, right, &n, &tmp, &lwork, &info FCONE FCONE);
if (info != 0)
error(_("error code %d from Lapack routine '%s'"), info, "dgeev");
lwork = (int) tmp;
work = (double *) R_alloc(lwork, sizeof(double));
F77_CALL(dgeev)(jobVL, jobVR, &n, xvals, &n, wR, wI,
left, &n, right, &n, work, &lwork, &info FCONE FCONE);
if (info != 0)
error(_("error code %d from Lapack routine '%s'"), info, "dgeev");
complexValues = false;
for (i = 0; i < n; i++)
/* This test used to be !=0 for R < 2.3.0. This is OK for 0+0i */
if (fabs(wI[i]) > 10 * R_AccuracyInfo.eps * fabs(wR[i])) {
complexValues = true;
break;
}
SEXP ret = PROTECT(allocVector(VECSXP, 2));
SEXP nm = PROTECT(allocVector(STRSXP, 2));
SET_STRING_ELT(nm, 0, mkChar("values"));
SET_STRING_ELT(nm, 1, mkChar("vectors"));
setAttrib(ret, R_NamesSymbol, nm);
SET_VECTOR_ELT(ret, 1, R_NilValue);
if (complexValues) {
SEXP val = allocVector(CPLXSXP, n);
for (i = 0; i < n; i++) {
COMPLEX(val)[i].r = wR[i];
COMPLEX(val)[i].i = wI[i];
}
SET_VECTOR_ELT(ret, 0, val);
if (vectors) SET_VECTOR_ELT(ret, 1, unscramble(wI, n, right));
} else {
SEXP val = allocVector(REALSXP, n);
for (i = 0; i < n; i++) REAL(val)[i] = wR[i];
SET_VECTOR_ELT(ret, 0, val);
if(vectors) {
val = allocMatrix(REALSXP, n, n);
for (i = 0; i < (n * n); i++) REAL(val)[i] = right[i];
SET_VECTOR_ELT(ret, 1, val);
}
}
UNPROTECT(3);
return ret;
}
/* Real, symmetric case of eigen */
static SEXP La_rs(SEXP x, SEXP only_values)
{
int *xdims, n, lwork, info = 0, ov;
char jobv[2] = "U", uplo[2] = "L", range[2] = "A";
SEXP z = R_NilValue;
double *work, *rx, *rvalues, tmp, *rz = NULL;
int liwork, *iwork, itmp, m;
double vl = 0.0, vu = 0.0, abstol = 0.0;
/* valgrind seems to think vu should be set, but it is documented
not to be used if range='a' */
int il, iu, *isuppz;
xdims = INTEGER(coerceVector(getAttrib(x, R_DimSymbol), INTSXP));
n = xdims[0];
if (n != xdims[1]) error(_("'x' must be a square numeric matrix"));
ov = asLogical(only_values);
if (ov == NA_LOGICAL) error(_("invalid '%s' argument"), "only.values");
if (ov) jobv[0] = 'N'; else jobv[0] = 'V';
/* work on a copy of x, since LAPACK trashes it */
if (!isReal(x)) {
x = coerceVector(x, REALSXP);
rx = REAL(x);
} else {
rx = (double *) R_alloc(n * (size_t) n, sizeof(double));
Memcpy(rx, REAL(x), (size_t) n * n);
}
PROTECT(x);
SEXP values = PROTECT(allocVector(REALSXP, n));
rvalues = REAL(values);
if (!ov) {
z = PROTECT(allocMatrix(REALSXP, n, n));
rz = REAL(z);
}
isuppz = (int *) R_alloc(2*(size_t)n, sizeof(int));
/* ask for optimal size of work arrays */
lwork = -1; liwork = -1;
F77_CALL(dsyevr)(jobv, range, uplo, &n, rx, &n,
&vl, &vu, &il, &iu, &abstol, &m, rvalues,
rz, &n, isuppz,
&tmp, &lwork, &itmp, &liwork, &info FCONE FCONE FCONE);
if (info != 0)
error(_("error code %d from Lapack routine '%s'"), info, "dsyevr");
lwork = (int) tmp;
liwork = itmp;
work = (double *) R_alloc(lwork, sizeof(double));
iwork = (int *) R_alloc(liwork, sizeof(int));
F77_CALL(dsyevr)(jobv, range, uplo, &n, rx, &n,
&vl, &vu, &il, &iu, &abstol, &m, rvalues,
rz, &n, isuppz,
work, &lwork, iwork, &liwork, &info FCONE FCONE FCONE);
if (info != 0)
error(_("error code %d from Lapack routine '%s'"), info, "dsyevr");
SEXP ret, nm;
if (!ov) {
ret = PROTECT(allocVector(VECSXP, 2));
nm = PROTECT(allocVector(STRSXP, 2));
SET_STRING_ELT(nm, 1, mkChar("vectors"));
SET_VECTOR_ELT(ret, 1, z);
} else {
ret = PROTECT(allocVector(VECSXP, 1));
nm = PROTECT(allocVector(STRSXP, 1));
}
SET_STRING_ELT(nm, 0, mkChar("values"));
setAttrib(ret, R_NamesSymbol, nm);
SET_VECTOR_ELT(ret, 0, values);
UNPROTECT(ov ? 4 : 5);
return ret;
}