Open12時間前にコメント追加4

Benign Overfitting(良性過学習)

 定義訓練誤差が0、テスト誤差が(データ量に対して任意の)小さい値になること

 研究線形分類、回帰、NTK,2層NNで証明がされている

 線形の場合https://www.alphaxiv.org/abs/1906.11300
https://www.jmlr.org/papers/volume24/22-1398/22-1398.pdf

 ニューラルネットの場合(2層まで)
 Benign Overfitting in Two-layer Convolutional Neural Networkshttps://arxiv.org/abs/2303.04145

https://www.alphaxiv.org/ja/overview/2202.06526v3

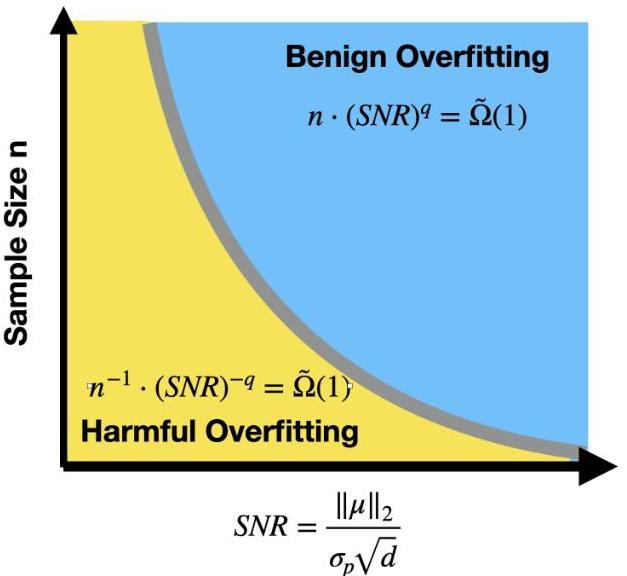
データのSNRが重要

https://github.com/uclaml/Benign-Overfitting-CNN/tree/main

 主張n \cdot \text{SNR}^q = \tilde{\Omega}(1)

 証明手法SGDにおけるSignal Noise分解

\mathbf{w}_{j,r}^{(t)} = \mathbf{w}_{j,r}^{(0)} + j \cdot \gamma_{j,r}^{(t)} \cdot \|\mu\|_2^{-2} \cdot \mu + \sum_{i=1}^n \rho_{j,r,i}^{(t)} \cdot \|\xi_i\|_2^{-2} \cdot \xi_i

 Benign Overfitting without Linearity: Neural Network Classifiers Trained by Gradient Descent for Noisy Linear Datahttps://www.alphaxiv.org/abs/2202.05928v5

2022〜2025　44ページ

https://speakerdeck.com/ryotaushio/benign-overfitting-in-neural-networks

”全てのデータがSupport Vectorになる”

 定理
 証明手法データ分布に対する仮定
NTK(線形に帰着できる)でない場合

sub-Gaussian
上記の仮定は、我々が導入する\lambda強対数凹性の仮定の導入を除いて、線形設定におけるChatterji and Long [CL21b]によって使用されるものと一致することに注意する。

この仮定は、強対数凹分布に対するLipschitz関数の集中不等式を用いるために必要である。

このデータモデルのバリエーションが最近研究されていることにも注意する[WT21; LR21; Wan+21]。

• (P_{\text{clust}} = P_{\text{clust}}^{(1)} \times \cdots \times P_{\text{clust}}^{(p)})は、周辺分布がすべて平均ゼロで、劣ガウスノルムが最大1である積分布である。

• P_{\text{clust}}は、ある\lambda \gt 0に対してR^p上の\lambda-強対数凹分布である。

• ある\kappa \gt 0に対して、(E_{z \sim P_{\text{clust}}}[\lVert z \rVert^2] \geq \kappa pが成り立つ。
帰納的分析: 著者らは、クリーンなテストポイントに対する非正規化マージンや重みノルムの成長など、勾配降下を通じて主要な量の進化を追跡します。
代理PL不等式: 損失関数に対してPolyak-Łojasiewicz不等式の一種が確立され、非凸最適化ランドスケープにもかかわらず収束保証を可能にします。
勾配相関制御: 高次元の幾何学が活用され、異なるサンプルからの勾配間の相関を制約し、訓練中の破壊的な干渉を防ぎます。
重みノルムの制約: 重みは大幅に成長するものの（NTKレジームから逸脱）、その成長は適切な汎化特性を維持するのに十分な程度に制御されます。

 Benign Overfitting in Two-layer ReLU Convolutional Neural NetworksReluのﾉ場合も証明できるらしい

 overparametrizationその他概念の関係次元性の仮定の緩和: 実際によくあるn>pであるが総パラメータ数mp>nの場合に、良性過適合は発生しうるか？

xiangze

 DNNに限らないBenign overfittingSoft Inductive bias,Bengn overfitting(良性過学習)という概念でPAC bayes理論に基づきoverparametrization, double descentなどの説明を試みている。解の有効次元、データに対する体積の増え方という考え方が特異学習理論と共通するかもしれない。

Deep Learning is Not So Mysterious or Different

Soft Inductive biasは Residual Pathway Priors (RPPs) として

Residual Pathway Priors for Soft Equivariance

Constraints

に起源をもつらしい。

紹介スライド

https://docs.google.com/presentation/d/1TLnCElJZAcqm3ZK8ANj3iHNT8-OXl1MHJysPhEto1MI/edit?slide=id.g36b072f2857_0_49#slide=id.g36b072f2857_0_49

https://olanleed.hatenablog.com/entry/2025/06/28/173851
https://speakerdeck.com/ryotaushio/benign-overfitting-in-neural-networks?slide=5

 ChatGPT o3による実証実験提案https://chatgpt.com/c/6861056c-868c-8008-af89-785947959aee

「この論文の主張を支持するような機械学習モデル、データセットを使った数値実験としてどのようなものが考えられるでしょうか」

 解答
 論文の主張benign overfitting やdouble descent はニューラルネット固有の挙動ではなく，他のモデルでも見られる」
その一般化挙動は PAC-Bayes や countable-hypothesis bounds といった従来枠組みで説明できる」

 Benign overfittingを線形回帰モデルで再現する

要素
推奨設定

モデル
ノンパラメトリックな最小ノルム解を得るために ridge = 0 (α → 0) の線形回帰．scikit-learn なら Ridge(alpha=1e-12, fit_intercept=False) が手軽です。

データ

Synthetic high-d regression：
d = 5 000 次元の i.i.d. 標準正規特徴，n = 1 000 サンプル．真の重みはスパース (例: 50 個だけ非ゼロ) に設定し，ラベルに独立ノイズ ε~𝒩(0, σ²) を加える。

手順
d を固定し n を 100→1 000 まで増やしつつ，
1. α=0（補間）と α>0（弱正則化）の両方で学習 2. 訓練 MSE = 0 を確認 3. テスト MSE が σ² 未満になる「benign現象」を確認

期待結果
Bartlett et al. が解析した「統計的に妥当な補間解」を線形回帰でも観測でき，ニューラルネット特有ではないことを実証できる。 (jmlr.org, arxiv.org)

 カーネル回帰でdouble descent曲線を描く

要素
推奨設定

モデル

Kernel Ridge Regression (KRR) with RBF kernel．バンド幅 σ をスケジューリングして「モデル複雑度」を連続的に変化させると理論と整合的な DD が現れます。

データ

Fashion-MNIST 1 000 サンプル（白黒28×28）や CIFAR-10 10 000 サンプル （32×32×3） —— 高次元かつ中規模で扱いやすい。

手順
1. λ=0（補間），λ>0（正則化）を固定したまま σ を小→大へ掃引，
2. または σ を固定し λ を 1e-2→1e-8→0 と掃引し，
3. 訓練/テスト誤差をプロットすると U 字→再下降の二峰性が出る。

参考文献
Belkin et al. の PNAS 論文 (2019) および最近の「Kernel bandwidth sweep で DD が現れる」報告． (pnas.org, arxiv.org)

 決定木系モデルで “ニューラル以外” の汎化性(double descent)を示す

要素
推奨設定

モデル

Gradient Boosted Decision Trees (GBDT, XGBoost / LightGBM)
学習器数 (n_estimators) を 10→10 000 まで指数的に増加．

データ

Higgs UCI dataset (11 M サンプル → 抽出 100 k) や UCI Adult (45 k) —— 木モデルが得意なタブラー。

観測
標準的な shrinkage (η) を 0.1 以下に保ちつつ木数を増やすと，学習誤差 0 近傍でテスト誤差が再び低下する “木版ダブルディセント” を再現可能（再解析で確認済み）。

注意
ランダムフォレストでは DD が観測されにくいとの反証報告もあるので，GBDT と RF を並べると議論が深化します。 (arxiv.org, proceedings.neurips.cc)

 PAC-Bayes / Countable-Hypothesis Bounds を実装比較

ステップ
具体例

① 事前分布 P(θ)
線形回帰：N(0, τ²I) — Closed-form.
MLP：He 初期化と同等の Gaussian.

② 事後分布Q(θ | D)
重み空間に対し “fractional posterior” Q_β ∝ P(θ)·exp(−β·L(D,θ)) を数値近似（SGD + SWAG で共分散推定）。

③ バウンド評価
Catoni の単純な PAC-Bayes bound Δ = √((KL(Q‖P)+ln(2√n/δ))/2(n−1)) を比較し，線形・KRR・MLP すべてで同オーダの一般化ギャップを確認。

④ データセット

UCI Abalone（回帰）と CIFAR-10（分類）で実施すると，「モデルサイズではなく KL が支配」という Wilson の主張が可視化される。

 表現学習が「残る違い」であることを示す補助実験Deep CNN (ResNet-18) と random Fourier features + logistic regression を 同じ CIFAR-10 で訓練し，線形プローブ：最終層手前の特徴を固定し，小規模線形分類器を別途訓練。
CNN では線形プローブ精度 ≫ RFF モデル本体，→ 深層モデル特有の表現学習効果を定量化。
これにより「一般化挙動は共通枠組みで説明できるが，表現学習の質はニューラルが優位」という Wilson のバランス論を支持。

 実装ワンポイント

テーマ
scikit-learn / PyTorch 実装ヒント

データ生成

numpy.random.randn(n,d)，真の w に np.random.randn(d); w[sparse_idx]=0

DD 曲線

np.logspace でハイパラ掃引 → matplotlib で訓練・テスト曲線プロット

PAC-Bayes

torchdistributions で KL，SWAG 実装は swag ライブラリが楽

再現性
乱数シード固定，5 fold クロスバリデーションで分散可視化

 まとめ線形,カーネル,ツリー モデルでBenign Overfitting, double decentが生起し，ニューラルネット専有ではないことを実証できる。
PAC-Bayes 的解析 で「仮説空間の大きさではなく 選ばれる分布の KL が鍵」というソフト誘導バイアス視点を共有可能。
一方で 表現学習能力 のNNそれ以外のモデルの差異を定量化することで，Wilson が言及する「深層学習の相対的特長」も合わせて検証できる。
これらの実験パイプラインを組み合わせれば，論文の立場を実証的に支持しつつ，限界も含めたバランスの良い議論を構築できる。

 再現実験コードhttps://github.com/xiangze/soft_inductive_bias

要素	推奨設定
モデル	ノンパラメトリックな最小ノルム解を得るために ridge = 0 (α → 0) の線形回帰．scikit-learn なら `Ridge(alpha=1e-12, fit_intercept=False)` が手軽です。
データ	Synthetic high-d regression： d = 5 000 次元の i.i.d. 標準正規特徴，n = 1 000 サンプル．真の重みはスパース (例: 50 個だけ非ゼロ) に設定し，ラベルに独立ノイズ ε~𝒩(0, σ²) を加える。
手順	d を固定し n を 100→1 000 まで増やしつつ， 1. α=0（補間）と α>0（弱正則化）の両方で学習 2. 訓練 MSE = 0 を確認 3. テスト MSE が σ² 未満になる「benign現象」を確認
期待結果	Bartlett et al. が解析した「統計的に妥当な補間解」を線形回帰でも観測でき，ニューラルネット特有ではないことを実証できる。 (jmlr.org, arxiv.org)

要素	推奨設定
モデル	Kernel Ridge Regression (KRR) with RBF kernel．バンド幅 σ をスケジューリングして「モデル複雑度」を連続的に変化させると理論と整合的な DD が現れます。
データ	Fashion-MNIST 1 000 サンプル（白黒28×28）や CIFAR-10 10 000 サンプル（32×32×3） —— 高次元かつ中規模で扱いやすい。
手順	1. λ=0（補間），λ>0（正則化）を固定したまま σ を小→大へ掃引， 2. または σ を固定し λ を 1e-2→1e-8→0 と掃引し， 3. 訓練/テスト誤差をプロットすると U 字→再下降の二峰性が出る。
参考文献	Belkin et al. の PNAS 論文 (2019) および最近の「Kernel bandwidth sweep で DD が現れる」報告． (pnas.org, arxiv.org)

要素	推奨設定
モデル	Gradient Boosted Decision Trees (GBDT, XGBoost / LightGBM) 学習器数 (n_estimators) を 10→10 000 まで指数的に増加．
データ	Higgs UCI dataset (11 M サンプル → 抽出 100 k) や UCI Adult (45 k) —— 木モデルが得意なタブラー。
観測	標準的な shrinkage (η) を 0.1 以下に保ちつつ木数を増やすと，学習誤差 0 近傍でテスト誤差が再び低下する “木版ダブルディセント” を再現可能（再解析で確認済み）。
注意	ランダムフォレストでは DD が観測されにくいとの反証報告もあるので，GBDT と RF を並べると議論が深化します。 (arxiv.org, proceedings.neurips.cc)

ステップ	具体例
① 事前分布 P(θ)	線形回帰：N(0, τ²I) — Closed-form. MLP：He 初期化と同等の Gaussian.
② 事後分布Q(θ \| D)	重み空間に対し “fractional posterior” Q_β ∝ P(θ)·exp(−β·L(D,θ)) を数値近似（SGD + SWAG で共分散推定）。
③ バウンド評価	Catoni の単純な PAC-Bayes bound Δ = √((KL(Q‖P)+ln(2√n/δ))/2(n−1)) を比較し，線形・KRR・MLP すべてで同オーダの一般化ギャップを確認。
④ データセット	UCI Abalone（回帰）と CIFAR-10（分類）で実施すると，「モデルサイズではなく KL が支配」という Wilson の主張が可視化される。

テーマ	scikit-learn / PyTorch 実装ヒント
データ生成	`numpy.random.randn(n,d)`，真の w に `np.random.randn(d); w[sparse_idx]=0`
DD 曲線	`np.logspace` でハイパラ掃引 → `matplotlib` で訓練・テスト曲線プロット
PAC-Bayes	`torchdistributions` で KL，SWAG 実装は `swag` ライブラリが楽
再現性	乱数シード固定，5 fold クロスバリデーションで分散可視化

xiangze

 ステートメントの検証、批判総じて既存の研究事実の追認である
DNN以外のDDの存在、挙動は既に論文化されているものである。
パラメータを増大させた場合の挙動に関するステートメントは検証されていないし、特異学習理論で想定される挙動と同一かどうか、それを含むのかどうかも主張できていない。
PAC-Bayes boundの計算では明示的に事前分布を使っていて今回のコルモゴロフ複雑性を使った形式にはなっていない
コルモゴロフ複雑性の実例である圧縮アルゴリズムは例示されていない。
表現学習ではそもそもDNNは最終層を取り替えることができるで高性能になるというのは当たり前のようで主張が弱い

 上記に変わる実験提案Benign overfittingの再現　「構造化されたデータに対しては帰納的バイアスが低いモデルでも汎化する」
Solomonoff priorを使ったモデルのPAC-Bayes boundの実証(link)
次数に応じた正則化項(事前分布)の類似したより自然な概念
Surprises in High-Dimensional Ridgeless Least Squares Interpolationにおける　γ=n/p(データ数/パラメータ数)一定、あるいは変化させた場合のDNNでの対応事例
学習データを増やすと性能が悪化する？
二重降下の考え方を思い出すと、パラメータ数とデータ数の比率で、パラメータ数が膨大になることで汎化性能がもう一度下がるという話でした。したがって、同じパラメータ数であれば、データ数が増えることで汎化性能が悪くなる領域に戻ってしまうことも起きてしまいます。この現象は、多層ニューラルネットワークの世界においてはEMC（Effective Model Complexity）で説明されます
SLTにおける描像との対応付け
表現学習でのDNN１層分の表現能力の高さ(微分不可能関数などが近似できる)ことを主張する
上記批判を受けてChatGPT5は
A: 「汎化はパラメータ数でなく“符号長（=KL）”で制御」を圧縮→MDL事前で可視化
B: データ側のアルゴリズム的複雑さを段階的に上げると汎化性能が悪化（同じアーキ/optimizerでも）
C: ソフト拡張 vs ハード共有（畳み込み)でサンプル効率差を比較
D: SGDの単純性バイアス：バッチ/学習率でマージンとノルムがどう動くか
E: ヘッシアン退化（近零固有値比と汎化ギャップの関係を小規模で観測

を提唱

https://github.com/xiangze/soft_inductive_bias/blob/master/critics_experiment.py

xiangze

ヘッシアン退化は