深層学習が多層の膨大なパラメータを学習できる雰囲気を理解する

はじめに

筆者のモチベーション

本記事のキーワードは、

• 普遍近似定理（Universal Approximation Theorem）
• 二重降下（Double Descent）
• 過剰パラメータ化（Over-parameterized）
• 多層化の利点（Benefits of Depth）

といった感じで、これらのトピックを解説した素晴らしい和文資料は既にたくさん存在します。

https://qiita.com/mochimochidog/items/ca04bf3df7071041561a

https://ibis.t.u-tokyo.ac.jp/suzuki/lecture/2020/intensive2/Kyusyu_2020_Deep.pdf

https://ibisml.org/ibis2019/files/2019/11/slide_imaizumi.pdf

そんな中で「とりあえずこの記事を読めば深層学習がうまく学習できる雰囲気を掴める」記事を書くことを目標にしています。深層学習を取り巻くテーマは多岐にわたるため、論文を読み始めると NotebookLM を駆使したとしてもまだまだ大変な作業であり、各事柄を個別に解説した記事もいろいろ読まねばなりません。もちろん、DeepResearch 等を使えば本記事よりも多くの情報が得られるかもしれませんが、キュレーションしつつ詳しさに濃淡をつけながら、図を駆使した説明は2025年現在の DeepResearch では「とりあえずこの記事を読めば深層学習がうまく学習できる雰囲気を掴める」水準には達しないと思っています^[1]。「雰囲気を掴む」という表現をしていますが、字面だけの説明からは一歩踏み込んだ解像度の理解を目指したいと思います。

また、生成AIブームでAIに興味を持ち始めた方も増えています。そんな方々に、現在の生成AIそのものである深層学習の面白いポイントを是非伝えたいという気持ちもあります。

そして何よりも、アウトプットこそ最強の勉強法ということで、自身の勉強のためにも記事を書いています。

記事の内容に間違いがないように、論文を読みながら一所懸命書いてはいますが、レビューもなく独力で勉強した内容ですので、間違いなどが含まれる可能性が大いにあります。その際はコメントやX等で教えていただけますと幸いです。

膨大なパラメータの不思議

生成AI等でお馴染み、Transformer や Diffusion は多層ニューラルネットワーク（深層学習）によって実現されています。2025年現在での最先端 LLM に用いられているパラメータ数は非公開なものが多いですが、オープンソースモデルである Llama 3.1 では405B（B: Billion = 10億なので、405Bは4050億）ものパラメータを持っています。その他 GPT4 や Gemini2.5 などの非公開なモデルでは兆を超えるパラメータを持つとも言われています。

一方で、昔からある統計モデルを学んだ人は次の事実もご存じのはずです。

パラメータ数が多くなると過学習が起こりやすくなる

実際、線形回帰モデルにおいては特徴量の次元数がデータ数を上回るとき、任意のラベルを完全に再現できます。これは線形代数的に明らかで、$n$ 個のデータを $d$ 次元のベクトルで説明する場合、$d \geq n$ であればランクが $n$ になるため、任意の出力ベクトルに対してちょうど一致する係数ベクトルが求まります。さらに、クラス分類では、VC次元がデータ点集合数 $n$ 以上なら、任意のラベルで完全に分離できます^[2]。これらはデータがどんな分布であっても、ランダムに生成したデータであっても成り立ちます。

そこで、古典的な統計学では赤池情報量基準を用いてモデルを選んだり、決定木では深さ、回帰分析では正則化パラメータを調整したりすることで、パラメータ数を調整しながら汎化性能を高めようとしてきました。しかし、近年のニューラルネットワークではデータ数をはるかに超えるパラメータ数を持つモデルが登場し^[3]、見事な汎化性能を誇っています。

さて、近年の驚くべき性能を誇る深層学習モデルは、どうやって過学習を回避しながら適切なパラメータを発見しているのでしょうか。そもそも言語や画像の生成など複雑なタスクを遂行できるモデルパラメータは存在するのでしょうか。その疑問を少しでも理解できるよう、勉強した内容を本記事で解説します。

もちろんこれには完全な答えはありません。
それでも、redtea なりに調べて分かった範囲のことを本記事では紹介していきます。

本記事の構成

本記事では、以下の流れで説明します。

1. そもそも解は存在するのか（普遍近似定理^[4]）
   • ニューラルネットワークは強い表現力を持ち、ほとんどの関数を近似できるパラメータが存在することを知る。
2. 存在する解は見つかるのか（過剰パラメータ化）
   • 適切なパラメータが存在することが分かったところで、それを発見できるのか。
     それは過剰パラメータ化によって発見できると理解できる。
3. 見つけた解は汎化するのか（二重降下）
   • 過剰パラメータ化によって訓練誤差がほぼ0の地点が見つかるのは良いが、パラメータ数増加に伴って汎化性能が低下する「バイアスバリアンストレードオフ」が起きるのではないかという疑問が生じる。
     そこで、バイアスバリアンストレードオフが生じない「二重降下」を確認し、汎化性能が高まる気持ちを理解する。
4. 汎化する解を見つけやすいのは何故多層なのか（近似誤差レート）
   • パラメータ数を過剰に増やしても汎化性能を高められるなら、浅いニューラルネットワークでも十分そうな気がするが、何故深い層のニューラルネットワークが必要なのかを考える。

深層学習の表現力

画像認識や機械翻訳にとどまらず、今日の生成AIのような複雑な関数までも表現できてしまうニューラルネットワークには、どれほどの表現力があるのでしょうか。

普遍近似定理

普遍近似定理（Universal Approximation Theorem）は次の事柄を主張しています。

2層以上のニューラルネットワークは、任意の連続関数を任意の精度で近似できる。

ただし、普遍近似定理はあくまでも存在定理であり、十分な大きなサイズのニューラルネットワークには良いパラメータが存在することを言っているだけで、そのパラメータをどのように見つけるかに関しては何も言っていません。すなわち、学習可能性や汎化問題とは分けて考える必要があります。一旦本章ではパラメータを見つける部分には触れず、存在性について確認します。

解説は以下の記事が詳しいです。

https://qiita.com/mochimochidog/items/ca04bf3df7071041561a

完全に理解するには時間がかかりますが、存在しそうなことだけはイメージで掴みましょう。いくつかシンプルな関数の重ね合わせで、シンプルな関数を近似するアニメーションを作りました。直観的な理解としては、ニューラルネットワークの1つの層の幅をどんどん増やせば、重ね合わせられる関数が増えます。そしてその重みをいい感じにすれば、どんな形も描けるというものです^[5]。

ステップ関数で2次関数を近似する様子。

ReLU関数で2次関数を近似する様子

ReLU関数で3次関数を近似する様子

数式的なイメージの話をすると、ReLU関数の差を用いればステップ関数のようなものが作れます。

$$\text{ReLU}(x) = \max(0, x) \\ \text{"step-like"}(x) = h \times (\text{ReLU}(x-a) - \text{ReLU}(x-b))$$

ステップ関数のような関数をReLUから作るイメージ。このようなステップ関数もどきが作れれば、それを組み合わせることで任意の関数が作れそうです。

もちろん、連続関数だけでなく、非連続な関数も近似できます。世の中のデータは非連続的な変化をするものも非常に多いです。

良いパラメータは見つかるのか

前章で良いパラメータが存在することがわかりましたが、それは現実的に見つけることはできるのでしょうか。

パラメータを見つける難しさ

ロジスティック回帰などのシンプルな機械学習モデルでは、損失関数は凸関数（以下の図）であり、勾配を下っていけば必ず最適解が見つかります。

損失関数が凸関数であれば、損失が下がる方向にパラメータを動かしていけば、必ず最適解が見つかります。凸関数（wikipedia）より引用。

一方で、深層学習の損失関数は非常に複雑な構造を持っています。パラメータ数が億を平気で超えるので、損失関数を可視化したり、全貌を把握することは困難ですが、次元圧縮などを駆使することで以下のような可視化がなされたことがあります。

次元圧縮などで可視化された深層学習の損失関数（$z$ 軸が損失で、$x,y$ 軸がパラメータ空間を表しています。図の左は skip connections を含まないニューラルネットワークの可視化で、右側は含むものです。モデル構造を工夫することでパラメータの見つけやすさが大きく変わってくることが示唆されています。　Visualizing the Loss Landscape of Neural Nets Figure 1 より引用。

見ての通りニューラルネットワークの損失関数の形状は通常、非常に複雑で、初期値の運次第ですが、確率的な揺らぎでいくつかの山を越えて、深い谷を見つけねばならないのです^[6]。ロジスティック回帰のような損失関数とは一線を画します。

しかし実際、この確率的勾配降下法は非凸な損失関数であっても、現実的な計算リソースと時間で、実用上申し分ない程良い"谷"を見つけられています。本章では訓練損失を小さくする"谷"を見つけやすくする工夫を紹介します。

損失ランドスケープの平坦性

本節では探索するパラメータ空間の「損失ランドスケープ（loss landscape）」の幾何学的性質に着目します。さまざまな論文で^[7]、損失関数の収束先が平坦であるほど、汎化性能が高いと研究されてきました^[8]。

直感的な理解としては以下の損失関数の可視化グラフをご覧ください。図左では、損失関数が低くなっているところが平坦であるのに対して、図右では比較的尖っています。

簡単な実験で得た損失関数の可視化グラフ。$z$ 軸が低いほど損失が低く優れた状況です。左側がミニバッチサイズを小さくして探索したときに収束したパラメータ空間のある区間、右側がミニバッチサイズを大きくした場合のものを表しています。

直感的な理解としては、損失関数の平坦な領域でパラメータが決まれば、パラメータが変化しても損失は大きく変動しません。このような領域にある解はテストデータというデータの変動にも強いだろうという考えに基づいています。また、ミニバッチサイズとパラメータが収束する領域の関連は以下のように整理できます。

• ミニバッチサイズが大きいとき: ノイズの少ない安定した勾配を計算するため、損失関数の鋭い"谷底"（Sharp Minima）に真っ直ぐ落ちていく傾向があります。この鋭い"谷"は、訓練データに特化しすぎた（過学習した）解であり、少しデータがずれる（テストデータになる）と損失が急激に悪化するおそれがあります。

• ミニバッチサイズが小さいとき: 勾配にノイズが含まれるため、このノイズが探索の助けとなり、鋭い谷底に囚われることなく、より幅の広い"平坦な谷底"（Flat Minima）を見つけやすくなります。平坦な領域は、パラメータが多少変化しても損失が安定しているため、未知のデータに対しても頑健で、高い汎化性能を持つと考えられます。

2025年現在、損失関数の平坦性と汎化性能の関連は単純な因果関係（平坦であれば汎化する）とは思われていませんが、深く関わっているとは考えられている、と私は思っています。このように、汎化しやすい解を見つける工夫によって過学習を防ぐという考え方があります。

過剰化したパラメータが損失がほぼ0の地点を見つけてくれる

ある性能を達成するのに必要以上にパラメータを増やすこと（over-parametrization）で、解を見つけやすくする取り組みもあります。いわゆる次元の祝福と言われるものですが、一部のパラメータ更新では損失を下げられなくなっても、他のパラメータを増やすことで下げらる可能性が高まります。すなわち、イメージとしては過剰なパラメータがあれば、パラメータをどんな初期値で始めても、そこから辿り着ける損失がほぼ0の地点が存在し、結果として適切なパラメータを見つけられるという考え方です。

また、Du らの研究によると、過剰パラメータ化したニューラルネットワークに対して勾配降下法を適用すれば、損失関数が非凸目的関数にもかかわらず、訓練損失がほぼ0を達成できることを示しています。損失関数が凸関数であれば勾配降下を繰り返せば必ず損失が最も小さいところに移動できますが、そうでないなら、幸運か膨大な時間をかけなければ見つけられないはずです。この研究のすごいところは、非凸な形をしていても、必ず線形的な時間で損失がほぼ0になる地点が見つかることを示している点です^[9]。雰囲気は以下の通りです^[10]。

損失を以下のように定義します。

$$L(\theta) = \frac{1}{2} \sum_{i=1}^n (f(\theta,x_i) - y_i)^2$$

ここで、

• $f(\theta, x_i)$ は、データ $x_i$ に対するニューラルネットワークの予測値です。
• $y_i$ は、データ $x_i$ の正解ラベルです。
• $\theta$ は、ニューラルネットワークのすべてのパラメータです。

勾配降下法を適用すると、訓練中の各ステップ（イテレーション）$k$ における残差（正解と予測の差）$y - u(k)$ の変化は、近似的に以下の式で表すことができます。

$$y - u(k+1) \approx (I - \eta G(k)) (y - u(k))$$

この式は、次のステップでの残差が、現在の残差に $(I - \eta G(k))$ という行列をかけることで得られることを示しています。

• $I$ は単位行列
• $\eta$ は学習率（勾配降下法のステップサイズ）
• $G(k)$ は、訓練中のニューラルネットワークのパラメータ $\theta(k)$ によって誘導されるグラム行列

このグラム行列 $G(k)$ の各要素は、異なるデータ点に対する予測値の、パラメータに関する勾配（変化の方向）の内積によって定義されます。簡単に言うと、この行列は、訓練中のニューラルネットワークが、パラメータを微小に変化させたときに、異なるデータ点に対する予測値がどれだけ似た方向に変化するかを示す指標と考えることができます。

そしてこのグラム行列 $G(k)$ の特徴は、ニューラルネットワークの「幅」$m$（隠れ層のニューロン数）が十分に大きい場合、訓練プロセス全体を通じて $G(k)$ が、訓練データとネットワークの構造にのみ依存する固定の行列 $K^{(H)}$ に非常に近い状態を保つ ことです。つまり、$G(k) \approx K^{(H)}$ と近似できるのです。

このグラム行列の安定性は、主に二段階で説明されます。

1. 初期化段階での安定性: ランダムに初期化されたネットワークのグラム行列 $G(0)$ が、固定の行列 $K^{(H)}$ に近い。
2. 訓練中の安定性: 訓練が進むにつれても、グラム行列 $G(k)$ が初期状態の $G(0)$ に近い状態を維持する。

この安定性により、残差のダイナミクスは先の式のように近似的に線形に振る舞います。この近似的な線形ダイナミクスにより、訓練損失 $L(\theta(k))$ は、グラム行列 $K^{(H)}$ の最小固有値 $\lambda_{\min}(K^{(H)})$ に応じた線形速度で減少します。

論文では、ネットワークの幅 $m$ が十分に大きく、学習率 $\eta$ が適切に設定されていれば、$\lambda_{\min}(K^{(H)})$ がゼロよりも厳密に大きい定数（例: $\lambda_0/2$）以上に保たれることを証明しています。これにより、訓練損失は線形レートで減少し、最終的にほぼゼロに収束することが示されます。

つまり、全体としての損失関数は非凸であっても、過剰パラメータ化によって、勾配降下法による損失の減少は線形システムを最適化しているかのように振る舞うため、全域（グローバル）最小解（= 訓練損失ゼロの点）に到達できるのです^[11]。

膨大なパラメータで汎化する矛盾

訓練誤差ゼロを達成する解が無数に存在する中で、なぜ学習アルゴリズムは未知のテストデータに対しても「良い」解を見つけ出すことができるのでしょうか。それを紐解く二重降下に焦点を当てます。

パラメータ数が膨大になると、汎化性能が低下するということは統計の教科書によく書かれており、それはバイアスバリアンストレードオフで説明できます。

本章では、まずバイアスバリアンストレードオフを理解し、その後、それが成り立たない二重降下（Double Descent）が実験的にも、数学的にも成立することを確認し、膨大なパラメータで過学習が起きない理由を知ることを目指します。

バイアス-バリアンストレードオフ

言葉自体は聞いたことがある方は多いと思います。

概要

機械学習において、モデルの予測誤差はバイアス、バリアンス、ノイズの3つの成分に分解できます。ノイズは、データに含まれる不確実性であり、根本的に削除不可能な誤差であるため、今回はノイズなしで説明します。その上で、バイアスとバリアンスに分解することをバイアスバリアンス分解と呼びます。これはモデルの性能を理解する上で重要な概念で、以下のようなイメージです。

$$E[(y - \hat{f}(x))^2] = \text{Bias}^2 + \text{Variance}$$

ここで、バイアス（Bias） とは、真の関数 $f(x)$ とのズレを表しています。これが高いのは、モデルの表現力不足を意味します。一方、バリアンス（Variance） とは、異なる訓練データセットに対する予測のばらつきを表します。これはモデルの複雑さ（パラメータの多さ）に起因する不安定性を意味します。両者はトレードオフの関係にあり、片方を下げると片方が高くなってしまう性質があるので、そのバランスをとることが重要と、従来の統計学の教科書には書かれています。

左から順に、バイアスが高い状態、バリアンスが高い状態、バランスをとっている状態を作図しました。

簡単な多項式回帰での例です。薄い近似曲線はリサンプリングごとのモデル曲線を表します。

この図の内容を整理すると以下の通りです。

状態	モデルの複雑さと特徴	訓練誤差	テスト誤差
高いバイアス (Underfitting)	モデルが単純すぎて、データの特徴を捉えきれていない。	高い	高い
高いバリアンス (Overfitting)	モデルが複雑すぎて、データのノイズまで学習してしまっている。	低い	高い
バランスが良い (Good Fit)	モデルの複雑さが適切で、データの主要な特徴を捉えられている。	低い	低い

理解のポイントとしては、異なるデータセットで何度も推定した時、バリアンスが高い状態だとモデルが安定せず、大きく異なるモデルを推定してしまいます。図上段（左）と（中）の薄い近似曲線を見比べると、モデルのばらつきが（中）の方が大きいことが見て取れます。これこそが、バリアンス（モデルのばらつき）が大きい状態と理解できるポイントです。

二重降下（Double Descent）

二重降下（Double Descent）とは、先のバイアスバリアントレードオフが崩れるという衝撃的な内容です。

二重降下を表した図です。左（a）は古典的なパラメータ数が比較的少ないモデルでの挙動を表し、右（b）はモダンな大量のパラメータを持つモデルでの挙動です。横軸がモデルの表現力（すなわちパラメータ数）で、縦軸がテストデータに対する予測誤差のようなものを表しています。左（a）では、従来のバイアスバリアンストレードオフのように、序盤パラメータ数が増えるにつれて性能が向上しますが、パラメータが学習データを完全に覚えられるくらいになると、汎化性能が低下（バリアンスが上がる）して、U字の形をとります。一方、右（b）では、序盤こそ（a）と同様にU字型を描きますが、その後もパラメータ数を増やし続ければ汎化性能が高まるという２段階の誤差現象（Double Descent）が観測されます。Reconciling modern machine learning practice and the bias-variance trade-off Figure1 より引用。

パラメータ数がデータ点数よりもはるかに大きい場合（過剰パラメータ化の領域）に、予測性能（汎化性能）が向上するという、従来の統計学の常識に反する Double Descent は単なる経験則だけではなく、高次元の線形回帰モデルにおいて、数式を用いて定量的に説明できます。詳細を書くとそれだけで1つの記事になる勢いなので、ごくごくかいつまんで説明します。

https://arxiv.org/abs/1903.08560

1. 汎化性能（予測リスク）の定義と分解

まず、モデルの汎化性能は「予測リスク（prediction risk）」$R_X(\hat{\beta};\beta)$ によって評価されます。これは、訓練特徴量行列 $X$ で学習した推定器 $\hat{\beta}$ が、新しい（未観測の）テストデータ $(x_0, y_0)$ に対してどの程度正確な予測を行うかを示すものです。

予測リスクは、以下の式で定義されます。

$$R_X(\hat{\beta};\beta) = E[{({x_0}^T\hat{\beta} − {x_0}^T \beta)^2 |X] = E[ ||\hat{\beta} − \beta ||^2}_\Sigma |X ]$$

この予測リスクは、統計学でよく知られているように、バイアス（Bias） と バリアンス（Variance） の2つの成分に分解できます。

$$R_X(\hat{\beta};\beta) = \underbrace{||E[\hat{\beta}]|X)− \beta||^2_{\Sigma}}_{バイアス項 B_X(\hat{\beta};\beta)} + \underbrace{\text{Tr}[\text{Cov}(\hat{\beta}|X))\Sigma]}_{バリアンス項 V_X(\hat{\beta};\beta)}$$

これらの式展開の詳細

予測リスクの式展開

$$R_X(\hat{\beta};\beta) = E[({x_0}^T\hat{\beta} - {x_0}^T \beta)^2 |X] \\ R_X(\hat{\beta};\beta) = E[({x_0}^T(\hat{\beta} - \beta))^2 |X]$$

ベクトル $v = \hat{\beta} - \beta$ として、内積（スカラー）$a=x_0^T v$ とします。
$(x_0^Tv)^2=(x_0^T)(x_0^T)=v^T x_0 x_0^T v$
$\hat{\beta}$と$\beta$は$X$で条件づけているので定数と考えられるので、$v$も定数ベクトルです。よって、期待値の外に出すことができます。

$$R_X(\hat{\beta};\beta) = v^T E[{x_0} {x_0}^T |X] v$$

$x_0$ は訓練データ$x_i$と独立同一分布（iid）なので、$E[x_i]=0, \text{Cov}[x_i]=\Sigma$ が使えます。これを代入すると、

$$v^T E[{x_0} {x_0}^T |X] v = v^T \Sigma v = E[(\hat{\beta} - \beta)^T \Sigma \hat{\beta} - \beta))|X]$$

ノーテーションとして、$||x||^2_\Sigma = x^T\Sigma x$と書くことにすると、

$$E[||\hat{\beta} - \beta||^2_\Sigma|X]$$

が得られます。

バイアスバリアンス分解

$||\hat{\beta} - \beta||^2_\Sigma$ をバイアスバリアンス分解します。
まずは $\hat{\beta} - \beta$ の部分を考えますが、この手の計算ではよくあるように $E[\hat{\beta}|X]$ を間にかませます。

$$\hat{\beta} - \beta = (\hat{\beta} - E[\hat{\beta}|X]) + (E[\hat{\beta}|X] - \beta)$$

元の式に代入して展開します。

$$\begin{aligned} R_X(\hat{\beta};\beta) &= ||\hat{\beta} - \beta||^2_\Sigma \\ &= ((\hat{\beta} - E[\hat{\beta}|X]) + (E[\hat{\beta}|X] - \beta))^T \Sigma ((\hat{\beta} - E[\hat{\beta}|X]) + (E[\hat{\beta}|X] - \beta)) \\ &= ||E[\hat{\beta}|X] - \beta||^2_{\Sigma} + \text{Tr}[\text{Cov}(\hat{\beta}|X)\Sigma] \end{aligned}$$

ここで、

• バイアス項 $||E[\hat{\beta}|X] - \beta||^2_{\Sigma}$: 推定器の平均値が真の値 $\beta$ からどれだけ離れているかを示します。これはモデルが真の関数をどれだけ正確に表現できるかの能力に関わります。
• バリアンス項 $\text{Tr}[\text{Cov}(\hat{\beta}|X)\Sigma]$: 推定器が異なる訓練データセットに対してどれだけ変動するかを示します。これは、モデルが訓練データのノイズにどれだけ敏感であるかに関わります。

2. リッジレス最小二乗推定器のバイアスとバリアンス

特に深層学習モデルで広く用いられる「データを完全に補間する（訓練誤差がゼロになる）」モデルの性質を捉えるため、最小2乗ノルム（"ridgeless"）最小二乗補間を対象とします。これは、多数の解が存在する過剰パラメータ下での状況 ($p > n$^[12]) において、L2ノルムが最小となる解を選択するものです。

先のバイアス$||E[\hat{\beta}|X] - \beta||^2_{\Sigma}$　とバリアンス $\text{Tr}[\text{Cov}(\hat{\beta}|X)\Sigma]$ は、このリッジレス最小二乗推定器 $\hat{\beta}$ においては以下のように変形できます。

• バイアス: $B_X(\hat{\beta};\beta)=\beta^T \Pi \Sigma \Pi \beta$
• バリアンス: $V_X(\hat{\beta};\beta)= \sigma^2/n \text{Tr}[\hat{\Sigma}^+ \hat{\Sigma}]$

ここで $\hat{\Sigma}=X^T X /n$ は訓練データの標本共分散行列であり、$\Pi = I - \hat{\Sigma}^+ \hat{\Sigma}$ ^[13]は訓練特徴量行列 $X$ の零空間（Null Space）への射影行列です。$σ^2$ は $y$ に含まれるノイズの分散です。

この式の意味を雰囲気で理解する

論文中では、$E(x_i)=0$（中心化済）としていることに注意してください。

バイアス

$||E[\hat{\beta}|X] - \beta||^2_{\Sigma}$ が $\beta^T \Pi \Sigma \Pi \beta$ になることを確認します。

線形回帰のパラメータ推定は、不偏推定量で以下のように与えられます^[14]。

$$E[\hat{\beta}|X] = (X^T X)^{-1} X^T Y$$

ここで、逆行列の部分を一般化逆行列に置き換えると、

$$\begin{aligned} E[\hat{\beta}|X] &= (X^T X)^{+} X^T Y \\ &= (X^T X)^{+} X^T X \beta \\ &= \hat{\Sigma}^{+}\Sigma \beta \end{aligned}$$

となります。よって、

$$\begin{aligned} B_X(\hat{\beta};\beta) &= \lVert E[\hat{\beta}|X] - \beta \rVert^2_{\Sigma} \\ &= \lVert \hat{\Sigma}^{+}\Sigma \beta - \beta \rVert^2_{\Sigma} \\ &= \lVert (\hat{\Sigma}^{+}\Sigma - I)\beta \rVert^2_{\Sigma} \\ &= \beta^T \Pi \Sigma \Pi \beta \end{aligned}$$

ただし、$\Pi = I - \hat{\Sigma}^{+}\Sigma$ としています。$\Sigma$ と $\hat{\Sigma}$ の取り扱いを間違いやすい式ですので注意してください。

バリアンス

$\text{Tr}[\text{Cov}(\hat{\beta}|X)\Sigma]$ が $V_X(\hat{\beta};\beta)= \sigma^2/n \text{Tr}[\hat{\Sigma}^+ \hat{\Sigma}]$ になることを確認します。

まず、$\hat{\beta}$ の共分散行列を $X$ で条件づけて計算します。
$X$ が与えられたとき、$\hat{\beta}$ のランダム性はノイズ $\varepsilon$ のみに由来することに注意します（$y = X\beta + \varepsilon$）。

$$\begin{aligned} \text{Cov}(\hat{\beta}|X) &= \text{Cov}((X^T X)^+ X^T y | X) \\ &= (X^T X)^+ X^T \text{Cov}(y|X) ((X^T X)^+ X^T)^T \\ &= (X^T X)^+ X^T \text{Cov}(\varepsilon|X) X ((X^T X)^+)^T \end{aligned}$$

ここで、ノイズの共分散は $\text{Cov}(\varepsilon|X) = \sigma^2 I_n$ であり、$(A^+)^T = (A^T)^+$ という一般化逆行列の性質と、$X^TX$が対称行列であることを用いると、

$$\begin{aligned} \text{Cov}(\hat{\beta}|X) &= (X^T X)^+ X^T (\sigma^2 I_n) X (X^T X)^+ \\ &= \sigma^2 (X^T X)^+ X^T X (X^T X)^+ \end{aligned}$$

ムーア-ペルローズの一般化逆行列の性質 $A^+ A A^+ = A^+$ を用いると、$(X^T X)^+ X^T X (X^T X)^+ = (X^T X)^+$ と簡略化できます。よって、

$$\text{Cov}(\hat{\beta}|X) = \sigma^2 (X^T X)^+$$

となります。これをバリアンス項 $\text{Tr}[\text{Cov}(\hat{\beta}|X)\Sigma]$ に代入すると、

$$V_X(\hat{\beta};\beta) = \sigma^2 \text{Tr}[(X^T X)^+ \Sigma]$$

が得られます。一方、本文で示されている最終的なバリアンスの式は $V_X(\hat{\beta};\beta) = \sigma^2/n \text{Tr}[\hat{\Sigma}^+ \hat{\Sigma}]$ でした。
本文の表記 $\hat{\Sigma} = X^T X/n$ を使うと、これは以下のように展開できます。

$$\begin{aligned} \frac{\sigma^2}{n} \text{Tr}[\hat{\Sigma}^+ \hat{\Sigma}] &= \frac{\sigma^2}{n} \text{Tr}[ (X^T X / n)^+ (X^T X/n) ] \\ &= \frac{\sigma^2}{n} \text{Tr}[ n(X^T X)^+ (X^T X/n) ] \\ &= \frac{\sigma^2}{n} \text{Tr}[ (X^T X)^+ X^T X ] \end{aligned}$$

この結果と、我々が導出した $\sigma^2 \text{Tr}[(X^T X)^+ \Sigma]$ を比較すると、この等式は $\Sigma = \frac{1}{n}X^T X = \hat{\Sigma}$、つまり母共分散行列が標本共分散行列に等しいという仮定のもとで成り立ちます。
これは高次元の解析ではしばしば用いられる設定であり、この仮定を置くことで、バリアンス項がより簡潔な形で表現できるのです。

バイアスの見方に関する補足

• $p < n$ (underparametrized: パラメータ数 < データ点数)の場合

$X$ は通常フルカラムランクを持つため、$\Pi = 0$ となり、バイアス項はゼロになります。通常の線形回帰が不偏推定量（バイアス0）であることと符号します。

• $p > n$ (overparametrized: パラメータ数 > データ点数)の場合

$X$ はフルローランクを持ち（一般的に）$Π$ は非ゼロとなり、バイアス項はゼロになりません。正則化項つき線形回帰は不偏推定量ではなかったですよね。

3. 過剰パラメータ化における予測リスクの変化

ここまでは前座で、ここが肝です。パラメータ数 $p$ がデータ数 $n$ よりもはるかに大きくなる「過剰パラメータ化」の領域 ($\gamma = p/n > 1$　は一定値として、$p \rightarrow \infty, n \rightarrow \infty$ な状況) で、予測リスクがどのように変化するかは、特徴量の分布の仮定によって大きく異なります。この項では簡単のため、Isotropic Features（等方性特徴量モデル）の場合（$\Sigma = I_p$ すなわち特徴量が独立同分布で、共分散行列が単位行列である場合）を考えます。

まず、

• $r^2 = ||\beta||^2_2$ （推定したパラメータの二乗ノルム）
• $\gamma = p/n$
• $\gamma > 1$

とします。

先の項で、バイアス項は $\text{B}_X(\hat{\beta};\beta) = \beta^T\Pi\Sigma\Pi\beta$、バリアンス項は $\text{V}_X(\hat{\beta};\beta) = \sigma^2/n\text{Tr}[\hat{\Sigma}^+\Sigma]$ であることを既に示しています。これを過剰パラメータ化」の領域 ($\gamma = p/n > 1$　は一定値として、$p \rightarrow \infty, n \rightarrow \infty$ な状況) で極限をとると、

$$R_X(\hat{\beta};\beta) \rightarrow r^2 (1 - 1/ \gamma) + \sigma^2 / (\gamma - 1)$$

が得られ、この式からバイアス項とバリアンス項の挙動を個別に分析できます。

いきなり現れた漸近的な予測リスク $R_X(\hat{\beta};\beta) \rightarrow r^2 (1 - 1/ \gamma) + \sigma^2 / (\gamma - 1)$ の導出はとても大変なので、申し訳ないですが割愛します。。。

バイアス項 $r^2 (1 - 1/ \gamma)$ の挙動

$\gamma$ が1より大きくなると（$p$ が $n$ より大きくなるにつれて）、$1/\gamma$ は減少し、$1 - 1/\gamma$ は増加します。これは、バイアスが $\gamma$ の増加とともに増加することを意味します。

直感的な理解としては、$p > n$ の場合、最小ノルム推定器 $\hat{\beta}$ は、訓練データ行列 $X$ の行空間（次元 $n$ の部分空間）に制約されます^[15]（訓練データ全てを正確に補完するようにfitするので、真の $\beta$ とずれてしまいます）。$p$ が増えるほど、この $n$ 次元の行空間が全体の $p$ 次元空間を占める割合が少なくなるため、真の $\beta$ からのずれ（バイアス）が増加します。

同じことを言っていますがもう少し言い換えると、モデルが非常に複雑になり、$p$ が大きくなっても、推定器が学習できるのはあくまで訓練データが張る限られた $n$ 次元の部分空間の中だけです。この部分空間が全体の空間 ($p$ 次元) に対して相対的に小さくなるにつれて、真のパラメータがその空間の外にある可能性が高まり、結果としてバイアスが増えるという感じです。

バリアンス項 $\sigma^2 / (\gamma - 1)$ の挙動

$\gamma$ が1より大きくなると $\gamma - 1$ は増加し、$1 / (\gamma - 1)$ は減少します。これは、バリアンスが $\gamma$ の増加とともに減少することを意味します。

この現象は、パラメータが多くなればいろんな方法で訓練データ点を全て通る予測曲線を引けるようになるイメージを持っている方からすると、直感に反するように思えますが、次のように説明できます。$p$ が増えることで、最小2乗ノルムの最小二乗解は、係数をより多くの次元に分散させることが可能になります。これにより、解の2乗ノルムが一般的に減少し、これはあたかもモデルがより「正則化」されているかのような効果をもたらし、結果として分散が減少します。

以上をもって、等方性特徴量モデルのシンプルな線形回帰のケースにおいて、予測リスクが $\gamma=1$ の補間境界で発散し、その後 $\gamma > 1$ の領域で下降する現象が数学的に確認できました。この設定での様子を見てみましょう。

$\gamma=1$ のところで予測リスク（汎化性能）が悪化した後、回復する二重降下を確認しています。なお、線の違いはSNR（Signal to Noise Ratio）です（相対的なデータのノイズの大きさ）。Surprises in High-Dimensional Ridgeless Least Squares Interpolation
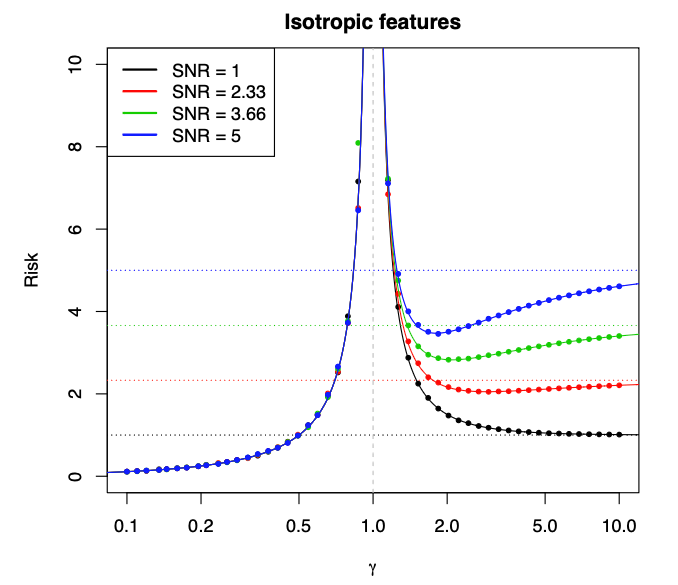
Figure 2 より引用。

ここでは設定がシンプルすぎるため、$\gamma > 1$ の領域がグローバルでリスクが最小になっていません。次項では条件を少し変えてた潜在空間モデルを見てみます。

潜在空間モデルの場合の二重降下

このモデルの基本的な設定は以下の通りです。

$$y_i = \theta^T z_i + \xi_i \quad (24) \\ x_{ij} = w_j^T z_i + u_{ij}$$

• $y_i \in \mathbb{R}$: $i$番目のデータポイントの応答変数（目的変数）です。
• $z_i \in \mathbb{R}^d$: $i$番目のデータポイントの潜在特徴量ベクトルです。これは直接観測されません。
• $\theta \in \mathbb{R}^d$: 潜在特徴量 $z_i$ に対応する真の係数ベクトルです。潜在空間において $y_i$ と $z_i$ の間に線形関係があることを示します。
• $\xi_i \sim N(0, \sigma_\xi^2)$: 応答変数 $y_i$ のノイズです。平均ゼロ、分散 $\sigma_\xi^2$ のガウス分布に従います。
• $x_{ij}$: $i$番目のデータポイントの観測される特徴量ベクトル $x_i \in \mathbb{R}^p$ の $j$番目の要素です。
• $w_j \in \mathbb{R}^d$: $j$番目の観測特徴量 $x_{ij}$ が潜在特徴量 $z_i$ からどのように生成されるかを示す重みベクトルです。この場合、$w_j^T$ は行列 $W$ の $j$ 行目を示し、$x_{ij}$ は $W$ の $j$行目と $z_i$ の内積にノイズを加えたものになります。
• $u_{ij} \sim N(0, 1)$: 観測される特徴量 $x_{ij}$ のノイズです。平均ゼロ、分散1の独立同分布のガウス分布に従います。

このモデルでは、データは低次元の潜在空間 ($z_i$) から生成され、観測される特徴量 ($x_i$) はその潜在特徴量のノイズを含む変換である、という構造を持っています。

この時の予測リスクの極限の導出も非常に大変なので割愛しますが、以下のような複雑な式になります（Surprises in High-Dimensional Ridgeless Least Squares Interpolation
Corollary 4. より）。

$$\begin{align} R_X(\hat{\beta};\beta)&\to \mathscr{B}_{\text{lat}}(\psi, \gamma) + \mathscr{V}_{\text{lat}}(\psi, \gamma) \\ \mathscr{B}_{\text{lat}}(\psi, \gamma) &:= \left\{1 + \frac{\gamma c_0}{\frac{\mathscr{E}_1(\psi, \gamma)}{\mathscr{E}_2(\psi, \gamma)}}\right\} \cdot \frac{r_\theta^2}{(1 + \psi)(1 + c_0\gamma(1 + \psi^{-1}))^2} \\ \mathscr{V}(\psi, \gamma) &:= \sigma^2\gamma c_0 \frac{\mathscr{E}_1(\psi, \gamma)}{\mathscr{E}_2(\psi, \gamma)} \\ \mathscr{E}_1(\psi, \gamma) &:= \frac{1 - \psi}{(1 + c_0\gamma)^2} + \frac{\psi(1 + \psi^{-1})^2}{(1 + c_0(1 + \psi^{-1})\gamma)^2} \\ \mathscr{E}_2(\psi, \gamma) &:= \frac{1 - \psi}{(1 + c_0\gamma)^2} + \frac{1 + \psi}{(1 + c_0(1 + \psi^{-1})\gamma)^2} \\ 1 - \frac{1}{\gamma} &= \frac{1 - \psi}{1 + c_0\gamma} + \frac{\psi}{1 + c_0(1 + \psi^{-1})\gamma} \end{align}$$

その結果、潜在空モデルでは $\gamma = p/n$ が1を超えるところから予測リスクが単調に減少し、$\gamma \to \infty$ の漸近的な極限でグローバルミニマムに達します。

Surprises in High-Dimensional Ridgeless Least Squares Interpolation
Figure 6 より引用。

これは一部私の解釈ですが、潜在空間モデルのような状況下では、以下の2つの事柄を考えられます。

過剰パラメータにおける予測リスクの単調減少の直感的理解

今回の設定は各特徴量ベクトル $x_i$ は、潜在変数 $z_i$ のノイズの多い測定と見なすことができます。もしノイズ $u_{ij}$ がなければ、観測特徴量 $x_i$ に対する最小ノルム回帰は、潜在変数 $z_i$ に対する最小ノルム回帰と等価になります。ノイズ $u_{ij}$ が存在する場合でも、「$p$ が大きくなるにつれて、ノイズは効果的に『平均化』され、 $z_i$ が直接観測される理想的な状況に近づく」 と考えられます。つまり、入力特徴量の次元を増やすことで、潜在特徴量 $z_i$ に関する情報がより多く抽出され、結果として予測性能が向上するというわけです。これは、真の信号が低次元の潜在空間に存在し、高次元の特徴空間がその信号の冗長な（しかし情報を持つ）表現を提供している場合に起こり得ます。この状況は微弱な情報を活用する AIの例に相当するものかと思っています。

https://joisino.hatenablog.com/entry/superai#微弱な情報を活用する-AI:~:text=01-15-,人間には認知できない情報を活用するAIたち,-正月休みに

正則化パラメータ $\lambda \rightarrow 0$ の直感的理解

大規模な過剰パラメータ化において、最適な正則化パラメータ^[16]の値は $\lambda \to 0$ になると論文中では説明されていますが、これの直感的理解を考えます。

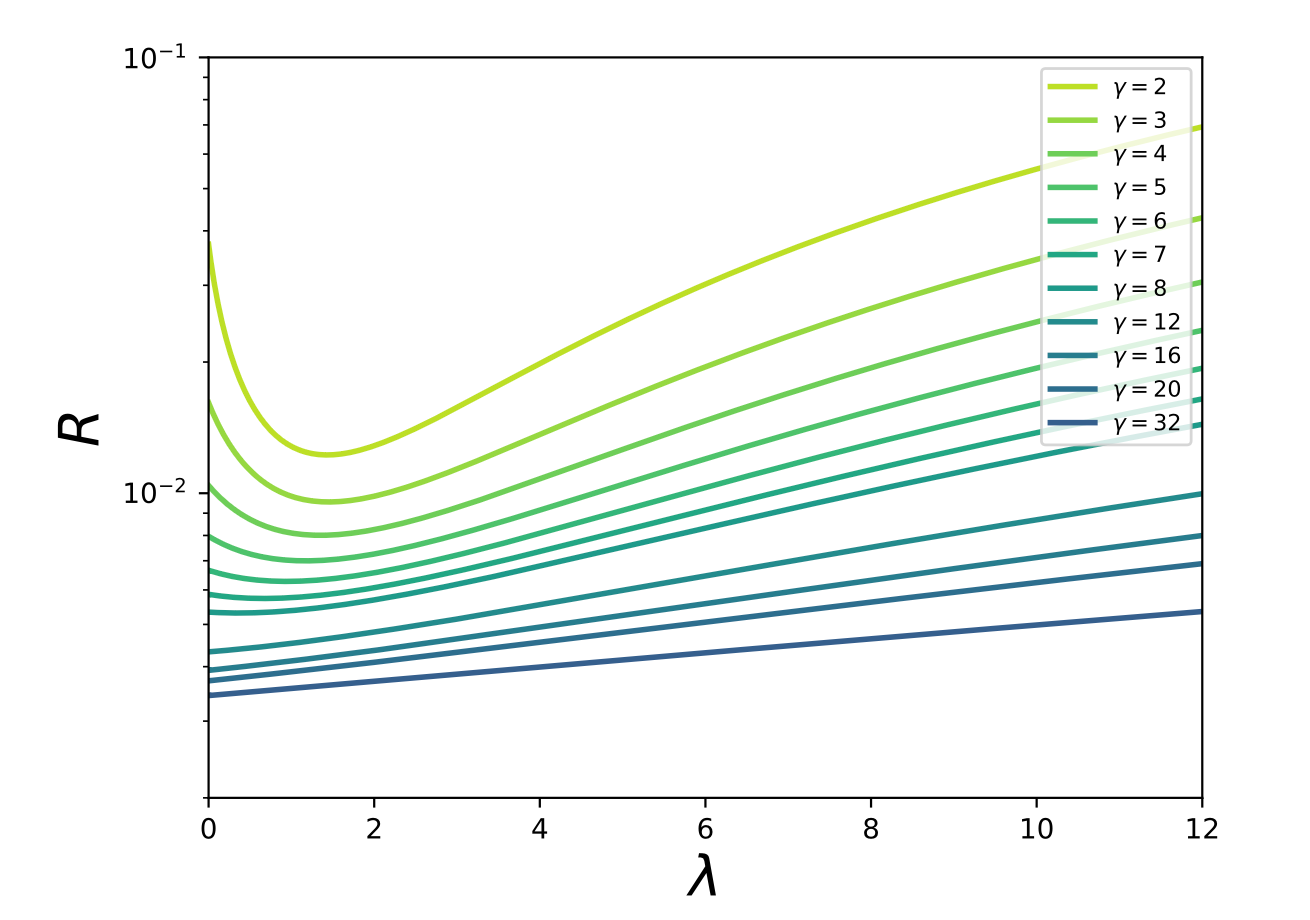
学習パラメータが増えるにつれて(パラメータ数と訓練データ数の比率を表している色に注目です)、最適な正則化パラメータ $\lambda$ が0に近づく様子です。 Surprises in High-Dimensional Ridgeless Least Squares Interpolation
Figure 10 より引用。

この現象は、モデルに入力ノイズが本質的に含まれている場合に、そのノイズが追加の正則化項として機能するという考え方で説明されます。特徴量行列 $X$ が、ノイズのない真の行列 $\bar{X} = ZW^T$ にノイズ行列 $U$ を加えたもの（$X = \bar{X} + U$）として見なせる場合、リッジ回帰のカーネル行列 $K(X,X) = XX^T/n$ は、おおよそ $K(\bar{X},\bar{X}) + U U^T/n$ となります。もし $U U^T/n$ がほぼ $I_n$ に比例するならば、これは有効な正則化項として働き、リッジパラメータ $\lambda$ を明示的に大きく設定する必要がなくなる（暗黙的正則化）、という直感的な説明です。

ただし、この暗黙的正則化の考え方は近年懐疑的な目で見られています。例えば Nagarajanらの研究では、暗黙的正則化だけでは過剰パラメータ化されたニューラルネットワークの優れた汎化性能を説明できないとしています。

左から2番目の図では、訓練データが増えるほど重みパラメータの2乗ノルムが増加している様子を表しています。暗黙的正則化が効くのであれば（左から3番目のようにテスト誤差が下がっている状況）、重みパラメータのノルムは0に近づくはずですが、そうはなっていない例です。Deep Double Descent: Where Bigger Models and More Data Hurt Figure 1より引用。Uniform convergence may be unable to explain generalization in deep learning Figure 1 より引用。

多層ニューラルネットワークでの二重降下

浅い層を持つリッジレス回帰だけでなく、深い層を持つモデルでも二重降下は現象として観測されています。例えば以下の図のように、ResNet18 のような多層ニューラルネットワークでもパラメータ数を増やし続けた時に二重降下が確認されています。

Deep Double Descent: Where Bigger Models and More Data Hurt Figure 1より引用。

学習データを増やすと性能が悪化する？

二重降下の考え方を思い出すと、パラメータ数とデータ数の比率で、パラメータ数が膨大になることで予測リスクがもう一度下がるとのことでした。したがって、同じパラメータ数であれば、データ数が増えることで汎化性能が悪くなる領域に戻ってしまうことも起きてしまいます。この現象は、多層ニューラルネットワークの世界においてはEMC（Effective Model Complexity）で説明されます（先の線形回帰の例での$\gamma = p/n$ に相当します）。

EMCは、様々な深層学習のタスクで見られる二重降下を統一的に説明することを目指して定義された指標です（が、経験的指標で、タスク依存性があることには注意です）。詳細はこの論文です。

https://arxiv.org/abs/1912.02292

訓練手順 $T$ の EMC は、平均してほぼゼロの訓練誤差を達成できる訓練サンプルの最大数 $n$ として定義されます。数式で表すと、分布 $D$ とパラメータ $\epsilon > 0$ に対して、

$$\text{EMC}_{D,\epsilon}(T) := \max \{n | E_{S \sim D^n} [\text{Error}_S(T (S))] \leq \epsilon \}$$

と表されます。ここで、$\text{Error}_S(M)$は訓練サンプル $S$ に対するモデル $M$ の平均誤差を示します。$\epsilon$ の値は通常、経験的に0.1などの小さな値が用いられます。

EMC が訓練サンプルの数 $n$ と同程度である臨界パラメータ化領域（Critically parameterized regime）において、モデルや訓練手順を変えると特異な振る舞いを示すといわれています。以下に整理します。

領域 (Region)	条件	モデルや訓練手順を複雑にした時のテスト誤差の変化
過少パラメータ化領域 Under-paremeterized regime	$\text{EMC} \ll n$	減少する
過剰パラメータ化領域 Over-parameterized regime	$\text{EMC} \gg n$	減少する
臨界パラメータ化領域 Critically parameterized regime	$\text{EMC} \approx n$	増加または減少

EMC の導入により、モデルパラメータ数以外でも生じる二重降下を説明できるようになりました。

• エポックごとの二重降下（モデルが固定されていても、訓練時間を増やすことで EMC が増加し、テスト性能が二重降下する）
• サンプル数の非単調性（訓練サンプルを増やすことで、データ数が EMC と近くなるポイント（テスト誤差がピークに達するところ）が右にシフトする効果と、誤差全体を下に下げる効果）

図左(a)は、は5層 CNN の、データセットサイズを変えた場合のモデルごとの二重降下を表します。上側は2倍のサンプル数で訓練してもテスト誤差が改善されないモデルサイズの範囲（緑色の網掛け）が生じます。下側は4倍のサンプル数で学習してもテスト誤差が改善されないモデルサイズの範囲（赤で網掛け）があります。図右（b）は、サンプル数が多いほど性能が低下する領域があることを示しています。Deep Double Descent: Where Bigger Models and More Data Hurt Figure 11 より引用。

二重降下（Double Descent）のまとめ

• 単純な線形回帰モデルでも、予測リスクが補間境界 ($p=n$) を超えた後、減少する現象が数式によって厳密に示すことができる。
• バリアンスがパラメータ数の増加とともに減少するという直感に反する現象が、L2ノルムが最小化される特性によって説明できる。
• この線形モデルから得られる知見は、非線形で複雑なニューラルネットワークにも適用できる可能性が示唆されており、実験的にその現象は確認されています。

（参考）三重降下（Triple Descent / Multiple Descent）

異なるランダム特徴を組み合わせて予測を行うアンサンブルモデルにおいて、一定の条件の元、3回以上の予測リスク降下も確認されています（あくまでも参考資料）。

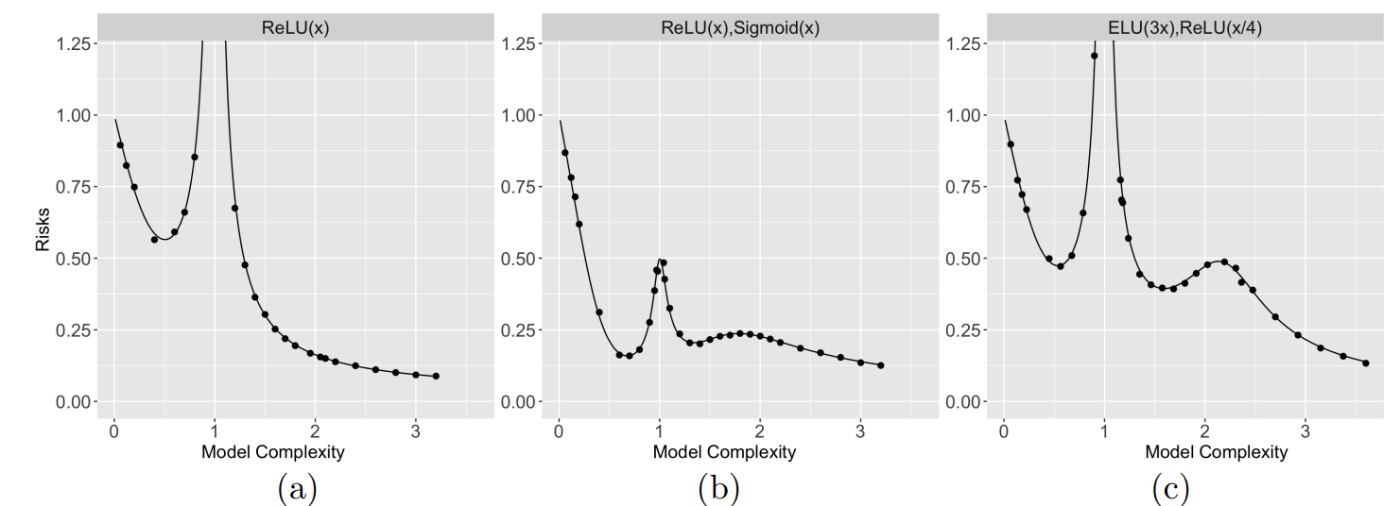
三重降下。Multiple Descent in the Multiple Random Feature Model Figure1 より引用。

スケーリング則

話の本筋からは外れてしまいますが、スケーリング則に触れないわけにもいかないという気持ちがあり、ちょっとだけ脱線します。

二重降下では「モデルがある規模を超えると一度性能が悪化し、その先でまた良くなる」という非単調性を見てきました。しかし実務では どこまでモデルを大きく、長く訓練するのが望ましいかを定量的に決めたい場面があります。

そこで近年は Neural Scaling Laws（NSL）という経験則が大規模実験と理論の両面から整備されつつあります。

パラメータ数とデータ数は別々に効く

言語モデルを対象とした Kaplan らの研究では、モデルサイズ $N$、学習トークン数 $D$、総計算量 $C$ を独立変数にし、各々が限定された言語モデルを考えたときの損失 $L$ は

$$L(N) = \left(\frac{N_c}{N}\right)^{\alpha_N} \\ L(D) = \left(\frac{D_c}{D}\right)^{\alpha_D} \\ L(C) = \left(\frac{C_c^{\min}}{C_{\min}}\right)^{\alpha_c^{\min}}$$

ここで、$\alpha_N \approx 0.076, N_c \approx 8.8\times 10^{13}, \alpha_D \approx 0.095, D_c \approx 5.4 \times 10{13}, \alpha^{\min}_c \approx 0.050, C^{\min}_c \approx 3.1 \times 10^8$ です。

さらにこれらを組み合わせて、モデルサイズ $N$ とデータサイズ $D$ の両方が同時に性能に与える影響を導出しています。

$$L(N,D) = \left[ \left(\frac{N_c}{N}\right)^{\frac{\alpha_N}{\alpha_D}} + \frac{D_c}{D} \right]^{\alpha_D}$$

このことから、指数の $\frac{\alpha_N}{\alpha_D}$ が効くので、計算予算 $C$ が固定なら優先的にモデルをやや大きめに作り、データ（トークン）をそこそこ使うのが適当ということが言えるかもしれません。

Chinchilla 則

Hoffmann らの研究 は 70M〜70B パラメータ、5B〜500B トークンのモデルを 400 個以上訓練し、

• 同じ FLOPS^[17] なら $N$ と $D$ は 等しくスケールさせるのが良い
• 実際に $N=70B, D=1.4T$ の Chinchilla^[18] が $N=280B, D=300B$ の Gopher^[19] を全ベンチで上回る

ことを実証しました。これは訓練データサイズ数より過剰なパラメータ数という状況になっていませんが、計算資源に見合っていない過剰パラメータ下ではモデルの潜在能力を引き出せていない状況になることを主張しています。

多層化の謎

これまでの章で、過剰パラメータ下において汎化するパラメータが見つかりそうな兆しは見えてきました。しかし、今までの議論では、1層あたりに大量のパラメータを持たせて、2~3層で構成する方法もあり得るはずです。一方で深層学習の進化の歴史は、AlexNet の8層から始まり、ResNet では数十～数百、現在では1000層を超えるモデルすら登場するなど、深層化の歴史と言えます。本章ではこの深層化の不思議を効率性の観点で説明していきます。

階層的合成による表現効率の良さ

定性的な説明

浅いネットワークと深いネットワークの最大の違いは、関数の作り方にあり、深いネットワークは複雑な関数を表現する際の効率が良いです（少ないパラメータで表現できます）。

浅いネットワークでは、幅を広げることで表現力を高めます。1つの隠れ層にニューロンをたくさん並べ、それらを足し合わせることで関数を表現します。これは、たくさんの単純な関数を並べて（例えば、記事前半で確認したReLU関数の重ね合わせの可視化）、目標の関数を少しずつ組み立てていくイメージです。これによって表現できる関数の複雑さを加算的に増大させられます。

深いネットワークでは、層を重ねることで表現力を高めます。層を1つ重ねることは、数学的には関数を1つ合成することに対応します。つまり、 $f(x) = g_L(\ldots g_2(g_1 (x)) \ldots)$ のように、前の層の出力を次の層の入力として、関数を入れ子にしていくことで、非常に複雑な関数を生成します。これにより、表現の複雑さを乗算的に増大させることができます。

この深いネットワーク特有の関数の合成という構造は、現実世界の問題を解く上で非常に有利に働きます。例えば、画像認識では、ピクセルがエッジを形成し、エッジが形を、形が物体を構成します。深い層を持つニューラルネットワークは、これらの中間的な特徴を各層で学習し、後の層で再利用することができます。この特徴の再利用こそが、深い層を持つニューラルネットワークが高い表現効率を達成できる理由の1つです。

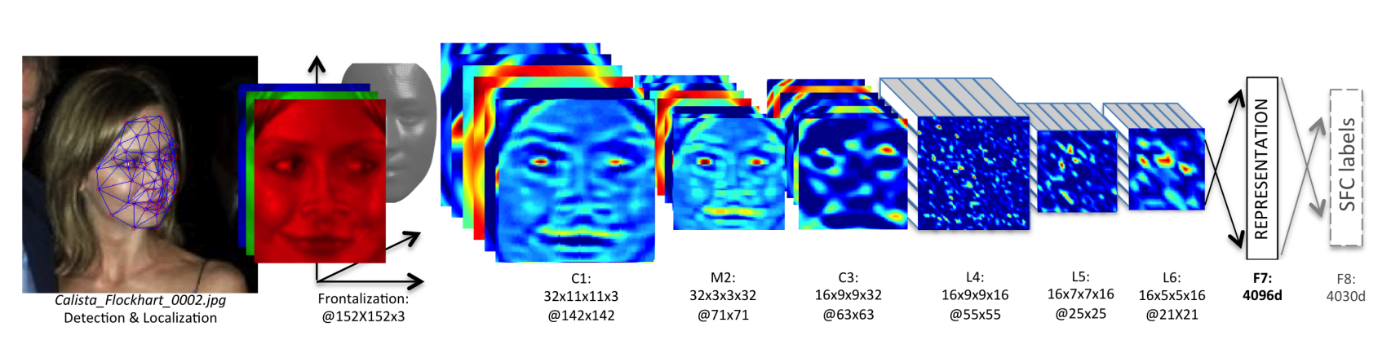
ニューラルネットワークの前半で特徴量を抽出している様子を表しています。DeepFace: Closing the Gap to Human-Level Performance in Face Verification Figure2 より引用。

数学による説明

この表現効率は数学的にも示されています。Benefits of depth in neural networks によると、$\Theta(k^3)$ 層の深いニューラルネットワークが、各層 $\Theta(1)$ 個のノードとパラメータであるとき、非常に複雑な関数（$\Theta(2^{k^3})$ オーダーの振動を持つ関数）を表現できます。一方それと同じ複雑さを持つ関数を、$O(k)$ 層の浅いニューラルネットワークが表現しようとすると、$\Omega(2^k)$ 個のパラメータが必要になるとしています。すなわち、層を $k^3$ に比例して増やすことで、浅いニューラルネットワークでは、$\Omega(2^k)$ （指数関数的）個のパラメータを増やすのに相当する複雑性を獲得できることを示しています。

$\Theta$ などの記法に馴染みがない方は以下の「漸近記法について」を開いてご確認ください。

漸近記法について

見る人が見ると怒られるような書き方をしていますが、本記事のモットーは雰囲気を理解することなので、雰囲気で書いてます。形式的な定義は Wikipedia をご覧ください。

• $\Theta$（big-theta: 上からも下からもおさえられる）
• $O$（big-o: 定数を選べば上からおさえられる）
• $o$（small-o: どんな定数倍をしても上からおさえられる）
• $\Omega$（big-omega: 下からおさえられる）

Wikipedia ランダウの記号:その他の漸近記法より

この主張の気持ちは、

• 層の数が少ないニューラルネットワークは表現できる振動の数が少ない
• 層の数が多いニューラルネットワークは多くの振動を表現できる
• 振動の数が少ない関数は振動の数が多い関数を近似できない

よって、層の深いニューラルネットワークは複雑な（振動の数が多い）関数を、層の浅いニューラルネットワークに比べて、はるかに近似しやすいのです。

深層化によって振動が増えることを掴むために、以下のような関数 $f$ を考えます。

$$f(z) = \sigma_R(2\sigma_R(z) - 4\sigma_R(z-1/2)) \\ \sigma_R(z) = \max(0, z)$$

（$\sigma_R$ はReLUですね）。
これは以下の図のように、三角波のような形をしています（右下のstep.6で三角波になっています）。

$f(z) = \sigma_R(2\sigma_R(z) - 4\sigma_R(z-1/2))$ の可視化。$x$方向にずらしたReLU関数の差をさらにReLU関数に通すことで、三角波が作れます。

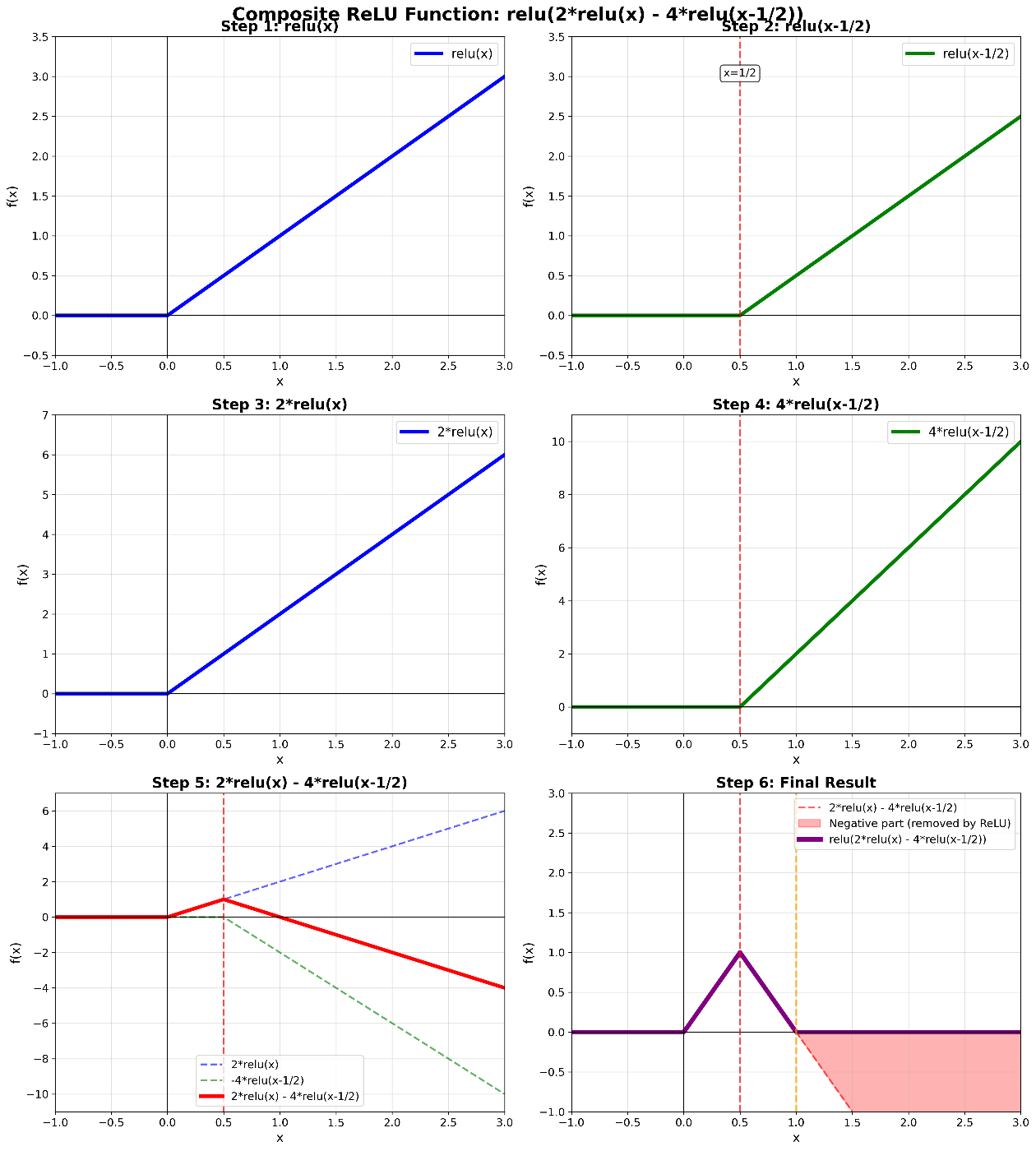
この関数は定数個のパラメータで表現できるので、1層、$\Theta(1)$個のノード、$\Theta(1)$個パラメータで実現できます。

深いニューラルネットワークの事情

この関数 $f$ を $k$ 回繰返し合成する（$f^k(z) = f(f(\cdots f(z) \cdots)$）ことで、その振動の数が指数的に増加します（$f^k(z)$ は $2^k + 1$ 個の振動を持ちます）。

$f^k$を計算するニューラルネットワークは、$f$ を計算する層を $k$ 回積み重ねることで構築できるので、このニューラルネットワークは $k$ 層持ち、各層は $\Theta(1)$ 個のノードで構成され、ネットワーク全体で $\Theta(1)$ 個のパラメータしか必要としません（同じ関数 $f$ を使い回すので）。合成関数は想像するのが難しく、言葉だけで書かれてもピンと来ないかもしれませんが、可視化すると雰囲気が掴めます。

$k$ 回合成した $f(f(\cdots f(z) \cdots)$ の可視化。左から右方向へ順に、$k=0,1,2$、下段は左から右方向へ$k=3,5,10$の場合を表しています。確かに $k$ に応じて指数関数的に振動が増えていっています。※振動の数え方は、直線の方向が変わる回数です^[20]。 $2^k + 1$ 回であることを数えてみてください。

浅いニューラルネットワークの事情

関数の振動をある閾値を跨ぐ回数として定義します。

$C_r(f)$: (Crossing Number): 関数 $f$ が、ある特定のしきい値（この論文では $1/2$）を横切る回数を表す指標です。

浅いニューラルネットワークでは、関数 $f$ が $(t, \alpha)$-poly（区分的多項式、すなわち $t$ 個の区間に分割され、各区間で次数が $\alpha$ 以下の多項式となる関数）である場合、$C_r(f) \leq t(1 + \alpha)$ という上限があります。したがって、振動数を増やすには、$t$（区間の数）または $\alpha$（多項式の次数）を増やす必要があります。

そして、1つの層で次数を増やすことは容易ではありません。同じ層内でノードを増やすことは、関数の足し算（または線形結合）に対応します。1つの層のノードを増やすような操作、すなわち2つの多項式を足し合わせると、結果として得られる多項式は、せいぜい項の数が2倍になり、多項式次数はどちらかの最大次数を超えることはありません。こういうわけで、振動数に寄与する項（$t$）は線形には増加しますが、指数的な増加は見られません^[21]。

高い振動数（多くの折れ曲がり）を効率的に得るには、これらの区分的線形関数をさらに重ねて合成することが必要であり、「深さ」には到底及ばないのです。

まとめ

ニューラルネットワークが作れる振動の数 $C_r(g)$ は、層の数 $l$ と総ノード数 $m$ を使って以下のように表されます。

$$C_r(g \circ h) ≤ 2(2tmα/l)^l \beta^{l^2}$$

その関係性は層の数 $l$ は指数部に、ノード数 $m$ は基数部に現れるという特徴があり、層の数が少ない浅いニューラルネットワークは、その分を幅（ノード数）で指数的に補う必要が出てしまいます。これこそが深さの重要な役割です。

私の感想ですが、深層学習の真髄は普遍近似定理ではなく、深層学習が持つアーキテクチャにあると思います。多層化されたニューラルネットワークによる合成的構造は、強力な帰納バイアス^[22]として機能しており、現実世界で頻繁に見られる階層的または合成的な構造を持つ関数の学習に適しています。深層学習のアーキテクチャ自体が、合成性を活用する解へと学習を誘導する一種の事前知識なのです。

近似誤差レートの改善

近似誤差レート（Approximation Error Rate）の観点でも考えてみましょう。先の表現効率の良さの話と雰囲気が似ているため、この節は簡単めな紹介にとどめます。

近似誤差レートとは、ニューラルネットワークがある関数を近似する際、パラメータを増やしたときの誤差の減少率を表します。$W$ 個のパラメータ集合 $\theta$ を持つニューラルネットワーク関数 $g_{\theta}(x)$ が、ある関数 $f(x)$ を近似する状況での近似誤差レートは、

$$\inf_{\theta} ||f - g_{\theta}|| = O(W^{-\alpha})$$

で表されます（$O$ はランダウの記号で、本記事でも既に雰囲気はお伝えしました）。この $\alpha$ が大きいほど、パラメータ数 $W$ を増やした時に効率的に関数を近似できることを意味します。この近似誤差レートとネットワークの深さの関係を見ていきましょう。

滑らかな関数の近似

まず、近似したい関数 $f(x)$ が十分に滑らか^[23]な場合を考えます。このとき、Barron による研究 では、1層のニューラルネットワークでの近似誤差レートは $\alpha=1/2$ であると示しています。これは特徴量の次元数 $d$ に直接依存しておらず、浅いニューラルネットワークでも、パラメータ数を増やせば、次元の大きさに関わらず、滑らかな関数を近似できることになります。滑らかな関数を相手にする場合は浅いニューラルネットワークで十分なのですが、現実世界で近似したい関数は滑らかとは限りません。次の項以降で複雑な関数の近似を見ていきます。

滑らかではない関数の近似

例えば画像のエッジ部分のような不連続な点や、音声波形のように尖った点を持つ関数は滑らかではありません。不連続な点や尖った点を表現するためには、その点の周辺に非常に多くのパラメータを集中させる必要があり、パラメータ効率が著しく低下します。この場合、近似誤差レートは入力特徴量次元 $d$ の影響を強く受け、$\alpha \approx 2/d$ 程度まで悪化してしまうことが Yarotskyの研究 で示されています。

しかし、（ReLU を活性化関数に持つ）深いニューラルネットワークは、前の節で見たように、層を重ねることで効率的に「折れ曲がり」を作り出し、滑らかでない関数の特異点^[24]を捉えて、近似誤差レートを改善すると示されました。

$$\text{Error (Shallow Net)} \propto W^{-2/d} \\ \text{Error (Deep Net)} \propto W^{-c})$$

$c$ は次元に依存しない定数なので、深いニューラルネットワークは近似誤差レートが有利になっています。

非均一な滑らかさを持つ関数の近似

最後に、非均一な滑らかさ（non-uniform smoothness）を持つ関数の近似を考えます。関数の大部分は非常に滑らかなのに、一部分だけが急激に変化したり、複雑な構造を持っていたりするような関数です。例えば、背景がぼやけた写真の中の、ピントが合った人物の輪郭などがこれにあたります。

深いネットワークはその階層構造を活かして、関数の場所ごとの滑らかさに応じてリソース（パラメータ）を効率的に配分できます。この「適応性」のおかげで、深いネットワークは非均一な滑らかさを持つ複雑な関数に対しても、高い近似誤差レートを維持できるのです。

深いニューラルネットワークは局所的に滑らかさを変えられます。深層学習の汎化誤差のための近似性能と複雑性解析 スライドp.14より引用。

結び

Zenn の記事にはアイキャッチ絵文字を設定できます。毎度毎度どの絵文字にしようか腐心するのですが、今回は「Deep Learningといえばイルカ！」^[25]ということで即断即決でした。多くの実務ですぐには役に立ちにくい話題でしたが、この手の話題は勉強していてとても楽しいですね。くどいようですが、誤りなどがございましたらコメント欄やXなどでご指摘いただけますと幸いです。

なお、本記事で引用元が明記されていない図やアニメーションは、Claude Code に筆者が指示して生成したPythonスクリプトから作ったものです。ソースコードの妥当性は筆者が目視で確認しています。

本記事のまとめ

• ニューラルネットワークはどんな関数も近似する強力な表現力を持つ（普遍近似定理）
• そして、過剰パラメータ化された状況で学習方法やモデルを工夫すれば、訓練誤差がほぼ0の"谷"を見つけることができる
• 過剰パラメータ化によって汎化する現象二重降下は、一部数学的にも経験的にも確認されている
• 多層化によって表現力が指数関数的に増加し、それは近似誤差レートの観点からも説明できる

参考文献

• A Survey on Universal Approximation Theorems, Midhun T Augustine, 2024.
• Benefits of depth in neural networks, Matus Telgarsky, 2016.
• DeepFace: Closing the Gap to Human-Level Performance in Face Verification, Yaniv Taigman, et al., 2014.
• Reconciling modern machine learning practice and the bias-variance trade-off, Mikhail Belkin, et al., 2018.
• Surprises in High-Dimensional Ridgeless Least Squares Interpolation
  , Trevor Hastie, et al., 2019.
• Deep Double Descent: Where Bigger Models and More Data Hurt Preetum Nakkiran, et al., 2019.
• Visualizing the Loss Landscape of Neural Nets, Hao Li, et al., 2017.
• On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima, Shirish Keskar et al., 2016.
• Fantastic Generalization Measures and Where to Find Them, Yiding Jiang et al., 2019.
• The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks
  , Jonathan Frankle, et al., 2018.
• Gradient Descent Finds Global Minima of Deep Neural Networks, Simon S. Du, et al., 2018.
• Universal approximation bounds for superpositions of a sigmoidal function, Andrew R. Barron, 1993.
• Error bounds for approximations with deep ReLU networks, Dmitry Yarotsky, 2017.
• Multiple Descent in the Multiple Random Feature Model, Xuran Meng, et al., 2024.
• Training Compute-Optimal Large Language Models, Jordan Hoffmann, et al., 2022.
• Scaling Laws for Neural Language Models, Jared Kaplan, et al., 2023.
• Uniform convergence may be unable to explain generalization in deep learning, Vaishnavh Nagarajan, J. Zico Kolter, 2019.
• 深層学習の原理に迫る, 今泉 允聡, 岩波書店, 2021.

脚注

1. 実際、Gmini2.5 pro とChatGPT o3 Pro でResearchしても達しなかったと感じたので、あれこれ調べながらこの記事を書きました。

2. ラベルの異なる点が重なっていたら分離できない、という突っ込みは一旦なしでお願いします。

3. パラメータ数とデータ数の関係はそれほど単純ではなく、帰納バイアスなども関わってきます。あくまでも雰囲気の話をします。

4. Universal Approximation Theorem. 万能近似定理と訳されることもあります。

5. フーリエ変換やテイラー展開のようなイメージを私は持っています。

6. ここまで興味を持って読んでくださった方であれば、深層学習は確率的勾配降下法によってパラメータ空間を探索していることはご存知のはずです。

7. [On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima(https://arxiv.org/abs/1609.04836) やFantastic Generalization Measures and Where to Find Them
   ]

8. ただし、完全に相関するわけではなく、逆の相関を示すケースも報告されています。

9. いくつかの前提条件がある点には注意です。

10. 厳密な証明は追いきれませんでした。

11. 論文中では特に、残差接続を持つ ResNet アーキテクチャは、一般的な全結合型ニューラルネットワークと比較して、必要な幅 $m$ の層数 $H$ への依存性が指数関数的から多項式に改善されると説明しています。

12. $p$ が次元数、$n$ がデータ数

13. $\hat{\Sigma}^+$ とは、ノルム最小型一般化逆行列解と呼ばれるものです。一般の行列は逆行列を持つとは限りませんが、そんな場合でも逆行列のようなものを求めたいときに用いる逆行列のようなものです。こちらの記事が詳しいです。

14. この推定量の導出はお手元の統計の教科書をご確認ください。

15. 訓練データは $p$ 列ありますが、データがそれよりも少ない $n$ 件なので、$n$ 列分の空間に制約されるという理解をしています。

16. これはハイパーパラメータです。

17. 1秒間に浮動小数点演算が何回できるかの指標値です。

18. Gemini 登場以前の DeepMind 製の大規模言語モデルです。

19. Gemini 登場以前の DeepMind 製の大規模言語モデルです。

20. 論文中では、ある閾値を跨ぐ回数で定義しています。

21. 言い換えです。個々のReLUゲートは入力空間に1つの「折れ曲がり」を導入しますが、1つの層で多くのReLUゲートを線形結合しても、その結果は区分的線形関数であり、折れ曲がりの数はノード数に比例してしか増えません。

22. 機械学習モデルが持っている仮定や構造のことです。ボールを投げた時の軌跡を予測する際、二次関数を用いることでデータに寄らない精度改善が見込めますが、これは立派な帰納バイアスです。Wikipediaも参照してください。

23. 無限回微分できるくらいの理解です。

24. 不連続点や尖った点のことです。

25. 深層学習という本から来ています。改訂第2版が出版されてから久しいですね。