はじめに
【情報数学】にてこの記事の目的について読んで頂けると幸いです。
線形代数のスクラップ
行列
数ベクトルに習ってもっと数を並べてそれが何かに使えるか考えてみます。
実数をm行n列に並べた\\
\quad\\
\begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n}\\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m1} & a_{m2} & \cdots & a_{mn}
\end{pmatrix}\\
\quad\\
をm×n行列といい、このような行列の集合全体をM_{m\times n}(\mathbb{R})で表す。
文脈によって\mathbb{R}は省略することが多いです。
行列の表現
一般的な行列の表現方法です。
\begin{aligned}
&(1)\quad
A=
\begin{pmatrix}
a_{11} & \cdots & a_{1j} & \cdots & a_{1n}\\
\vdots & \ddots & & & \vdots \\
a_{i1} & & a_{ij} & & a_{in} \\
\vdots & & & \ddots & \vdots \\
a_{m1} & \cdots & a_{mj} & \cdots & a_{mn}
\end{pmatrix}
のa_{ij}をAの(i,j)成分と呼ぶ\\
\quad\\
&(2)\quad
Aを単にA=(a_{ij})と書き表す。\\
&(3)\quad
Aの(i,j)成分を(A)_{ij}と書き表す。
\end{aligned}
行列は中身をいちいち全部書いていてはグチャグチャになるのでこのような表記法は必須です。
演算法則
k\in\mathbb{R},A,B\in M_{m\times n}(\mathbb{R})に対し、\\
\begin{aligned}
&(1)\quad A+B=(a_{ij}+b_{ij})\\
&(2)\quad kA=(ka_{ij})
\end{aligned}
つまるところ、数ベクトルと全く同じ和とスカラー倍を定義しました。お察しの通り、行列はこれで線形空間になります。
よし、これで行列が使える
使えません。
行列は和とスカラー倍が定義されただけではそれ自体に使い道はありません。
今、唯一分かることは行列が線形空間であり、数ベクトルとの深い関わりがありそうだという一点です。
どちらも線形空間なのだから、数ベクトルと行列の間には何かあるだろうという推測です。
行列の積
和とスカラー倍じゃ満足できないので積も定義します。
各成分をひたすら掛け算したいという欲求をおさえて有用な積を考えます。
とにかく次の定義を確認してください。
A=(a_{ij})\in M(l,m),B=(b_{jk})\in M(m,n)に対して、\\
AB\stackrel{\mathrm{def}}{=}(\sum_{j=1}^{m}a_{ij}b_{jk})\\
ただし、Aの列とBの行の数が一致しない場合は定義しない。
Aのi行の成分とBのk列の成分の総和を(AB)_{ik}とするということです。
ふざけるなと言いたいところですが、積をこのように定義することで極めて有用な使い道が生まれます。
演算法則
A,B,Cを積が定義できる行列,k\in\mathbb{R}に対し、\\
\begin{aligned}
&(1)\quad (AB)C=A(BC)\\
&(2)\quad k(AB)=(kA)B=A(kB)\\
&(3)\quad A(B+C)=AB+AC\\
&(4)\quad (A+B)C=AC+BC\\
\end{aligned}
ただし行列の積に交換法則は成立しません。
つまり、普通AB\not ={BA}です。
数ベクトルに行列を掛けてみる
M(n\times 1)は数ベクトルそのものです。さっき定義した積を利用して2次元数ベクトルに行列を掛けることができるわけです。
\begin{pmatrix}
3 &1\\
1 &2
\end{pmatrix}
\begin{pmatrix}
2\\
3
\end{pmatrix}
=
\begin{pmatrix}
9\\
8
\end{pmatrix}
これを図示するとこうなります。
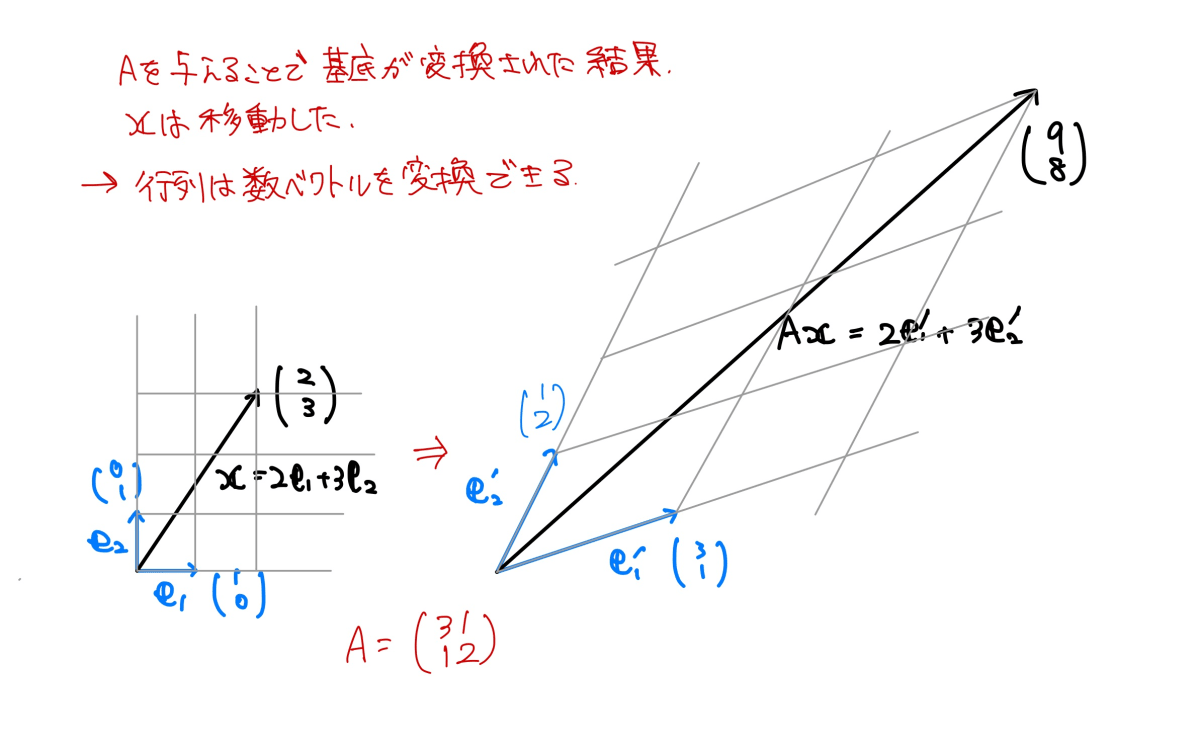
\mathbf{x}の標準基底が変換されて平面自体が斜めになりました。
よくみると行列の第1列が標準基底\mathbf{e}_1の変換先、第2列が標準基底\mathbf{e_2}の変換先に対応していることがわかります。この事実は変換後のベクトルを想像するのに役に立ちます。
後述の線形写像で一部分かることですが、行列の積はこのような数ベクトルの変換について何かと便利に扱えるようになっており、行列同士の積はこのような座標変換を合成することを意味します。
線形写像
行列の積の根源となる概念です。
定義
線形写像
f:\mathbb{R}^n\rightarrow\mathbb{R}^mが\forall\mathbf{x},\mathbf{y}\in\mathbb{R}^n,\forall k\in\mathbb{R}に対し\\
f(\mathbf{x}+\mathbf{y})=f(\mathbf{x})+f(\mathbf{y})\\
f(k\mathbf{x})=kf(\mathbf{x})\\
を満たすとき、fを\mathbb{R}^nから\mathbb{R}^mへの線形写像といい、この性質を線形性という。\\
また、m=nのとき、線形変換という。
核と像
線形写像fに対して\\
Ker(f)\stackrel{\mathrm{def}}{=}\{\mathbf{x}\in\mathbb{R}^n\mid f(\mathbf{x})=\mathbf{0} \}=f^{-1} (\mathbf{0})をfの核、\\
Im(f)\stackrel{\mathrm{def}}{=}\{f(\mathbf{x})\in\mathbb{R}^m\mid x\in\mathbb{R}^n \}をfの像という。
これに関しては今はまだほうっておいて大丈夫です。
定理1
証明
線形写像f:\mathbb{R}^n \to \mathbb{R}^m \colon \mathbf{x} \mapsto \mathbf{x'}について、各標準基底を\{\mathbf{e}_1,\dots,\mathbf{e}_n\},\{\mathbf{e'}_1,\dots,\mathbf{e'}_m\}とすると\\
\begin{aligned}
\mathbf{x'}
&=f(\mathbf{x})\\
&=f(x_1\mathbf{e}_1+,\dots,+x_n\mathbf{e}_n)\\
&=f(x_1\mathbf{e}_1)+,\dots,+f(x_n\mathbf{e}_n)\\
&=x_1f(\mathbf{e}_1)+,\dots,+x_nf(\mathbf{e}_n)\\
&=
\begin{pmatrix}
f(\mathbf{e}_1),\dots,f(\mathbf{e}_n)
\end{pmatrix}
\mathbf{x}
\end{aligned}\\
f(\mathbf{e}_i)\in \mathbb{R}^mであり、基底の定義よりf(\mathbf{e}_i)は\{\mathbf{e'}_1,\dots,\mathbf{e'}_m\}の線形結合で唯一に表せる。
これは素晴らしいです。行列を使甲斐があるってもんです。
定理2
f:\mathbb{R}^n\rightarrow\mathbb{R}^m,g:\mathbb{R}^m\rightarrow\mathbb{R}^lを線形写像とすると\\
合成写像g\circ f:\mathbb{R}^n\rightarrow\mathbb{R}^lも線形写像である。
証明
\begin{aligned}
(1)\quad
g\circ f(\mathbf{x}+\mathbf{x'})
&=g(f(\mathbf{x}+\mathbf{x'}))\\
&=g(f(\mathbf{x})+f(\mathbf{x'}))\\
&= g\circ f(\mathbf{x})+g\circ f(\mathbf{x'})\\
\end{aligned}
\begin{aligned}
(2)\quad
g\circ f(k\mathbf{x})
&=g(f(k\mathbf{x}))\\
&=g(kf(\mathbf{x}))\\
&=kg\circ f(\mathbf{x})\\
\end{aligned}\\
(1),(2)よりg\circ fは線形写像である。
行列同士の積も線形写像のままです。
行列の解釈
行列は線形空間に対する写像です。しかもどんな座標の変換に対しても一意的に対応し、なおかつ合成を行うことができます。
空間に対する超強力なアプローチができるわけです。

Discussion