Rustで数独解いてみた（数独の基本ルール）

Rustの勉強のため、前回、深さ優先探索のアルゴリズムで、数独を解くプログラムをRustで書いてみました。

https://zenn.dev/kuredev/articles/31f6852f4c23cd

今回は、参考書籍（Rubyで数独 (AIプログラミング入門)）の第2章の「基本ルールで解く」の内容をRustで書いてみました。

成果物は↓

https://github.com/kuredev/sudoku_rust/blob/main/src/basic_rule.rs

数独の基本ルール

書籍では数独において、あるセルの値が決定する際の基本ルールとして以下の2つが説明されています。

<ルールR1> あるブロックにおいて、ある数字が入るセルが1か所しかなければ、その数字はそのセルに入る。

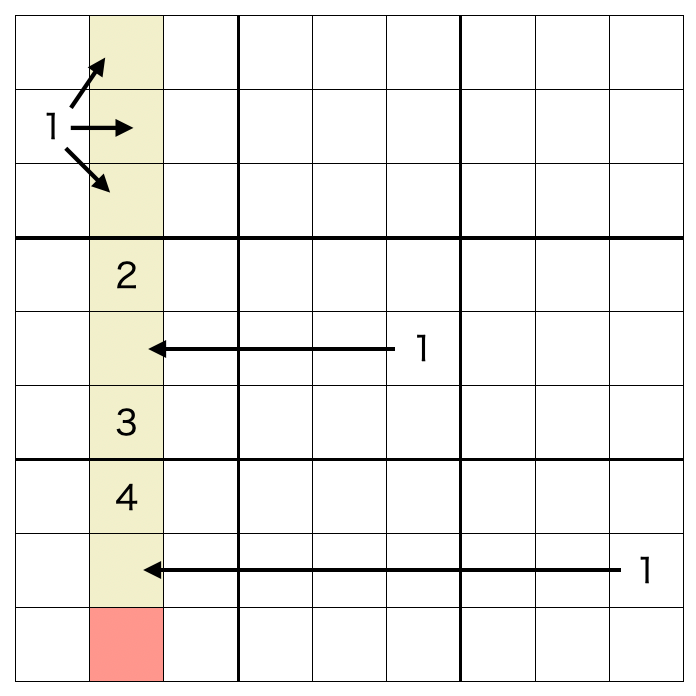
本書籍（本記事）での「ブロック」とは、行・列・3*3の正方形を総称した概念です。

<ルールR2> あるセルにおいて、ある数字以外の数字が入らないのであれば、その数字はそのセルに入る

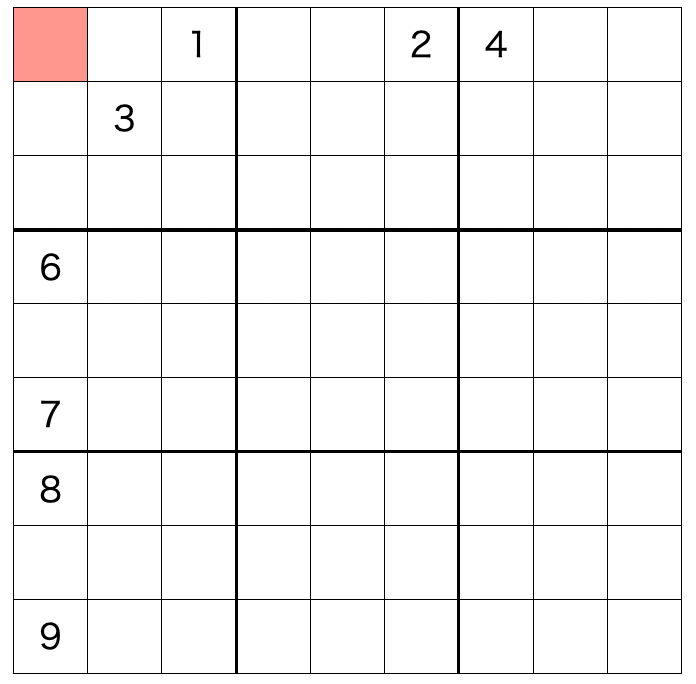
つまり、ルール1はブロックに、ルール2はセルに注目した考え方といえます。

加えて、書籍では（おそらく）アルゴリズムを整理するため、ルール0を定義しています。

<ルールR0> セルcの値が数字xに確定すると、セルcが属する3つのブロックの他のセルにはxが入らなくなる。

これらを踏まえたアルゴリズムは以下となります。

1. 数字の初期配置に基づいて、各セルに、代入不可能な数字の情報を伝達する（初期配置の制約伝搬）
2. 可能な限り、次のループを実行する
   a. ルールR1またはルールR2が適用される場所をすべて見つける
   b. その一つを選ぶ
   c. そのルールをその場所に適用する。R0を実行する

本記事では以上をベースにRustでプログラムを実装していきます。

Rustでの設計・実装

前回の記事ではアルゴリズムがシンプルだったため、構造体としては9*9全体を表すGridと座標を表すCoordinateくらいしか設計しませんでした。

今回は「ブロック」という概念が加わること、あるセルに代入可能な数値のリストを管理する必要があること等を鑑み、前回より構造体で扱えるデータを増やすこととしました。

// 盤面全体を表す
struct Grid([[Cell; 9]; 9]);

// ブロックを表す
struct Block([Cell; 9]);

// セルを表す
struct Cell {
    coodinate: Coordinate,
    number: i32,           // fix してない場合は 0
    possible_numbers: Vec<i32>,
}

// 座標を表す
struct Coordinate {
    x: CoordinateInt,
    y: CoordinateInt,
}

// 座標の数値を表す(1~9)
struct CoordinateInt(i32);

// セルがある値に確定したことを表す
struct FixedCell {
    cell: Cell,
    number: i32,
}

あとは必要なメソッドを構造体に当て込んでいきます。
例えばルール1を表現するメソッドは以下のように実装しました。ブロックという構造体を介して、そのブロックで代入可能な数値のリストを返す必要がある等、ブロックという単位で数値を扱う必要があるところが、実装においては複雑だったと思います。

    // あるブロックでは、その数字が入る可能性があるのは、そのセルだけ
    fn find_only_cell_in_block(&self) -> Option<FixedCell> {
        let blocks = self.get_blocks();
        for block in blocks.iter() {
            let not_assigned_numbers = block.get_not_assigned_numbers();
            for not_assigned_number in not_assigned_numbers {
                let cells = block.get_cells_can_assign_number(not_assigned_number);
                if cells.len() == 1 {
                    return Some(FixedCell{
                        cell: cells[0].clone(),
                        number: not_assigned_number
                    });
                }
            }
        }
        None
    }

実行結果

試しに実行すると以下のような出力を得られます。数値が決まっていく過程を1つずつ出力するようにすると、なかなか壮観です。

書籍にならって、まだ確定していないセルを ・ 、一行ずつ半角スペースを空けて表示させています。

実行結果

.8.....1. 1..2..9.. ..7..4..3 3...1..9. ...7.2... .6..8...4 9..4..1.. ..4..3..5 .2.....8. 
.8.....1. 1..2..9.. ..71.4..3 3...1..9. ...7.2... .6..8...4 9..4..1.. ..4..3..5 .2.....8. 
.8.....1. 1..2.89.. ..71.4..3 3...1..9. ...7.2... .6..8...4 9..4..1.. ..4..3..5 .2.....8. 
.8.....1. 1..2.89.. ..71.48.3 3...1..9. ...7.2... .6..8...4 9..4..1.. ..4..3..5 .2.....8. 
.8.....1. 1..2.89.. ..71.48.3 3...1..9. ...742... .6..8...4 9..4..1.. ..4..3..5 .2.....8. 
.8.....1. 1..2.89.. ..71.48.3 34..1..9. ...742... .6..8...4 9..4..1.. ..4..3..5 .2.....8. 
48.....1. 1..2.89.. ..71.48.3 34..1..9. ...742... .6..8...4 9..4..1.. ..4..3..5 .2.....8. 
48.....1. 1..2.894. ..71.48.3 34..1..9. ...742... .6..8...4 9..4..1.. ..4..3..5 .2.....8. 
48.....1. 1..2.894. ..71.48.3 34..1..9. ...742... 76..8...4 9..4..1.. ..4..3..5 .2.....8. 
48.....1. 1..2.894. ..71.48.3 34..1..9. ...742... 76.38...4 9..4..1.. ..4..3..5 .2.....8. 
48.....1. 1..2.894. ..71.48.3 34..1..9. ...742... 76.389..4 9..4..1.. ..4..3..5 .2.....8. 
48.....1. 1..2.894. ..71.48.3 34..1..9. ...742..1 76.389..4 9..4..1.. ..4..3..5 .2.....8. 
48.....1. 1..2.894. ..71.48.3 34..1..9. ...742..1 761389..4 9..4..1.. ..4..3..5 .2.....8. 
48.....1. 1..2.894. ..71.48.3 342.1..9. ...742..1 761389..4 9..4..1.. ..4..3..5 .2.....8. 
48.....1. 1..2.894. 2.71.48.3 342.1..9. ...742..1 761389..4 9..4..1.. ..4..3..5 .2.....8. 
48.....1. 1..2.894. 2.71.48.3 342.1..98 ...742..1 761389..4 9..4..1.. ..4..3..5 .2.....8. 
48.....1. 1..2.894. 2.71.48.3 342.1.798 ...742..1 761389..4 9..4..1.. ..4..3..5 .2.....8. 
48.....1. 1..2.894. 2.71.48.3 342.1.798 ...742..1 761389..4 9..4..1.. .14..3..5 .2.....8. 
48.....1. 1..2.894. 2.71.48.3 342.1.798 ...742..1 761389..4 97.4..1.. .14..3..5 .2.....8. 
48.....1. 1..2.894. 2.71.48.3 342.1.798 ...742..1 761389..4 97.4..1.. .14..3..5 .2...1.8. 
48.....1. 1..2.894. 2.71.48.3 342.1.798 ...742..1 761389..4 97.4..1.. .148.3..5 .2...1.8. 
48.....1. 1..2.894. 2.71.48.3 342.1.798 ...742..1 761389..4 97.4..1.. 6148.3..5 .2...1.8. 
48.....1. 1..2.894. 2.71.48.3 342.1.798 ...742..1 761389..4 97.4..1.. 6148.32.5 .2...1.8. 
48.....1. 1..2.894. 2.71.48.3 342.1.798 ...742..1 7613895.4 97.4..1.. 6148.32.5 .2...1.8. 
48....61. 1..2.894. 2.71.48.3 342.1.798 ...742..1 7613895.4 97.4..1.. 6148.32.5 .2...1.8. 
48....61. 1..2.8947 2.71.48.3 342.1.798 ...742..1 7613895.4 97.4..1.. 6148.32.5 .2...1.8. 
48....612 1..2.8947 2.71.48.3 342.1.798 ...742..1 7613895.4 97.4..1.. 6148.32.5 .2...1.8. 
48....612 1..2.8947 2.71.4853 342.1.798 ...742..1 7613895.4 97.4..1.. 6148.32.5 .2...1.8. 
48....612 1..2.8947 2971.4853 342.1.798 ...742..1 7613895.4 97.4..1.. 6148.32.5 .2...1.8. 
48....612 1..2.8947 297164853 342.1.798 ...742..1 7613895.4 97.4..1.. 6148.32.5 .2...1.8. 
48....612 1..2.8947 297164853 342.1.798 .5.742..1 7613895.4 97.4..1.. 6148.32.5 .2...1.8. 
48....612 13.2.8947 297164853 342.1.798 .5.742..1 7613895.4 97.4..1.. 6148.32.5 .2...1.8. 
485...612 13.2.8947 297164853 342.1.798 .5.742..1 7613895.4 97.4..1.. 6148.32.5 .2...1.8. 
4859..612 13.2.8947 297164853 342.1.798 .5.742..1 7613895.4 97.4..1.. 6148.32.5 .2...1.8. 
4859.7612 13.2.8947 297164853 342.1.798 .5.742..1 7613895.4 97.4..1.. 6148.32.5 .2...1.8. 
485937612 13.2.8947 297164853 342.1.798 .5.742..1 7613895.4 97.4..1.. 6148.32.5 .2...1.8. 
485937612 1362.8947 297164853 342.1.798 .5.742..1 7613895.4 97.4..1.. 6148.32.5 .2...1.8. 
485937612 136258947 297164853 342.1.798 .5.742..1 7613895.4 97.4..1.. 6148.32.5 .2...1.8. 
485937612 136258947 297164853 342.1.798 85.742..1 7613895.4 97.4..1.. 6148.32.5 .2...1.8. 
485937612 136258947 297164853 342.1.798 859742..1 7613895.4 97.4..1.. 6148.32.5 .2...1.8. 
485937612 136258947 297164853 342.1.798 8597423.1 7613895.4 97.4..1.. 6148.32.5 .2...1.8. 
485937612 136258947 297164853 342.1.798 859742361 7613895.4 97.4..1.. 6148.32.5 .2...1.8. 
485937612 136258947 297164853 342.1.798 859742361 761389524 97.4..1.. 6148.32.5 .2...1.8. 
485937612 136258947 297164853 342.1.798 859742361 761389524 97.42.1.. 6148.32.5 .2...1.8. 
485937612 136258947 297164853 342.1.798 859742361 761389524 97.42.13. 6148.32.5 .2...1.8. 
485937612 136258947 297164853 342.1.798 859742361 761389524 97842.13. 6148.32.5 .2...1.8. 
485937612 136258947 297164853 342.1.798 859742361 761389524 97842.136 6148.32.5 .2...1.8. 
485937612 136258947 297164853 342.1.798 859742361 761389524 978425136 6148.32.5 .2...1.8. 
485937612 136258947 297164853 342.16798 859742361 761389524 978425136 6148.32.5 .2...1.8. 
485937612 136258947 297164853 342516798 859742361 761389524 978425136 6148.32.5 .2...1.8. 
485937612 136258947 297164853 342516798 859742361 761389524 978425136 6148.3275 .2...1.8. 
485937612 136258947 297164853 342516798 859742361 761389524 978425136 614893275 .2...1.8. 
485937612 136258947 297164853 342516798 859742361 761389524 978425136 614893275 52...1.8. 
485937612 136258947 297164853 342516798 859742361 761389524 978425136 614893275 523..1.8. 
485937612 136258947 297164853 342516798 859742361 761389524 978425136 614893275 5236.1.8. 
485937612 136258947 297164853 342516798 859742361 761389524 978425136 614893275 523671.8. 
485937612 136258947 297164853 342516798 859742361 761389524 978425136 614893275 52367148. 
485937612 136258947 297164853 342516798 859742361 761389524 978425136 614893275 523671489

感想やメモ

最初はすべてのメソッドで参照を取り回して実装しようとしましたが、非常に複雑なハンドリングを必要となってしまったため、基本的にはロジックの計算部分は .clone して値だけをやり取りしつつ、値が確定したときだけ、 Grid のセルを参照で取ってきて、変更することとしました。そのように割り切ったら大分ハンドリングが楽になったため、参照を取り回すタイミングと、そうではないタイミングをきちんと整理しておくことが大事だなと骨身にしみました。

まだまだRust勉強したいところなので、次の課題にチャレンジしつつ、もう少しRust的な書き方を学んで今回とりあえず実装ですませたところのリファクタリングもしていきたいところです。