🤹‍♂️

Rustで数独解いてみた（深さ優先探索）

2024/04/17に公開

Rust

アルゴリズム

tech

Rust の勉強で数独を解くプログラムを書いてみました。
普段はRubyを書いているので、全体的に『Rubyで数独』を参考にしました。本記事は、本書の第1章をベースにRustに置き換えています。

リポジトリ

https://github.com/kuredev/sudoku_rust

参考書籍

https://amzn.to/3JiXcu3

アルゴリズム（深さ優先探索）

まず、数独を解くためのアルゴリズムを整理しておきます。内容としては、上記本の第1章「しらみつぶし法」の1種でアルゴリズムとしては「深さ優先探索」となります。

再帰を用いた深さ優先探索の実装は以下のような流れになります。

def dep(状態) # true or false
  if 状態は終了条件?
    true
  else
    可能性.each do |x|
       if dep(状態x)
          return true
       end
    end
    false
  end
end

「状態」とは今回でいえば、数独の9*9セル全体といえます。値が定まっていない空白のセルの1つの中で可能性のある数値のリストを抽出し、それを一つ定めて、次の空白のセルに進み、また可能性のある数値のリストを抽出し、一つ選んで・・を繰り返していきます。空白セルにも関わらず可能性のあるリストを出せなくなった場合は失敗となるため、一つ戻って別の候補を選んでまた進み・・を繰り返します。

数独のセル全体に対してどのように処理が進むかの序盤のイメージを以下図に示します。

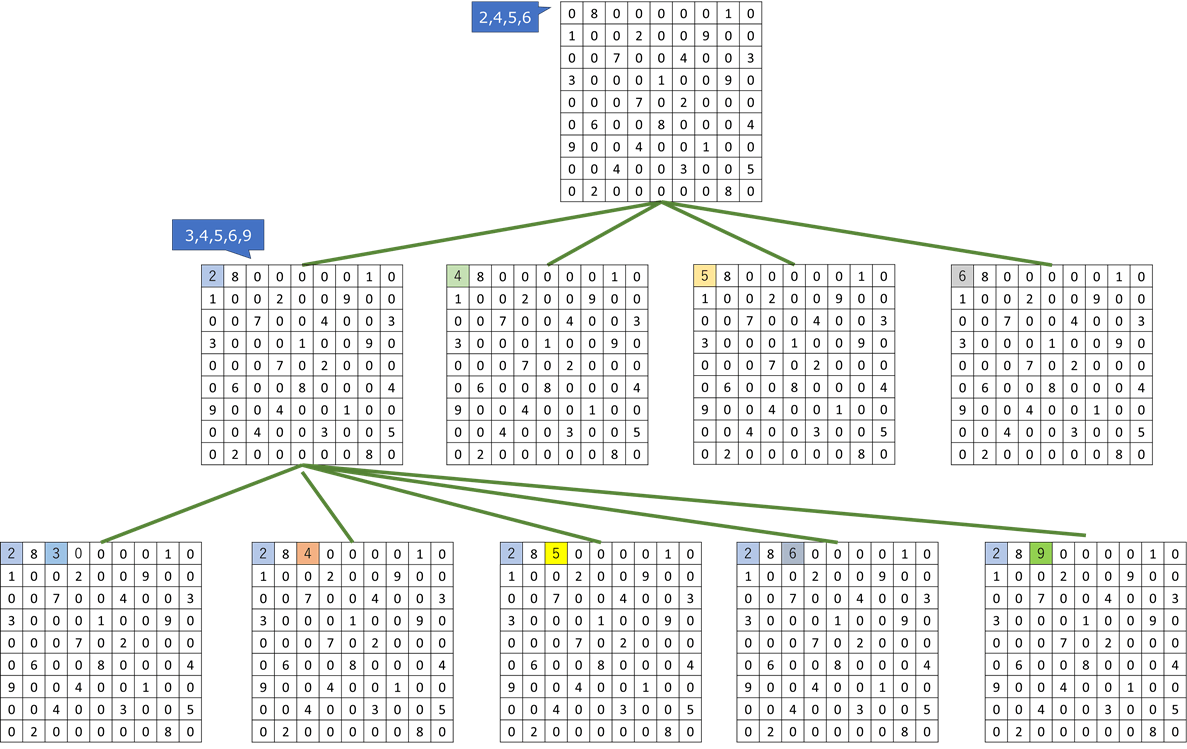
実装

上記をRustで実装してみました。

データの設計

まず1つのセルを i32 のデータとして扱います。空セルをどのように表現するかを悩みましたが、 None を扱い出すとプログラムで書かなければいけない処理が多くなりそうだったので、今回は 0 を空セルとして扱うこととし、シンプルに i32 の変数として扱うようにしました。

読みやすいように型エイリアスを設定します。

type Cell = i32;

座標として x, y の値を一緒に扱う必要があるので、座標の構造体を設定しました。

struct Coordinate {
    x: i32,
    y: i32,
}

盤面全体は 9*9 の配列を要素にもつ構造体を設定しました。この構造体にメソッドを追加していくこととしました。

struct Grid([[Cell; 9]; 9]);

アルゴリズムの実装

アルゴリズムを見ると、Gridに必要なメソッドとして以下が考えられます。

状態が終了条件を満たしているか？
特定の空セルの取得
特定の空セルが持ちうる値の可能性リストの取得

例えば、「状態が終了条件を満たしているか？」では、空セル（値が 0 のセル）が一つも無ければいいので、以下のように実装しました。

fn is_complete(&self) -> bool {
    for y in self.0.iter() {
        for x in y.iter() {
            if *x == 0 {
                return false;
            }
        }
    }
    true
}

その他のメソッドも実装し、これらを組み合わせて再帰関数として表現します。

fn solve(mut grid: Grid) -> bool {
    if grid.is_complete() {
        println!("complete!");
        grid.print();

        true
    } else {
        match grid.pick_empty_coordinate() {
            Ok(empty_coordinate) => {
                let possible_numbers = grid.get_possible_numbers(empty_coordinate.clone());

                for number in possible_numbers.iter() {
                    grid.0[empty_coordinate.y as usize - 1][empty_coordinate.x as usize - 1] = *number;
                    if solve(grid){
                        return true;
                    }
                }
                false
            },
            Err(error) => panic!("{}", error),
        }
    }
}

これを main 関数から呼び出します。Gridの入力も合わせて行います。

fn main(){
    let grid = Grid([
        [0,8,0,0,0,0,0,1,0],
        [1,0,0,2,0,0,9,0,0],
        [0,0,7,0,0,4,0,0,3],
        [3,0,0,0,1,0,0,9,0],
        [0,0,0,7,0,2,0,0,0],
        [0,6,0,0,8,0,0,0,4],
        [9,0,0,4,0,0,1,0,0],
        [0,0,4,0,0,3,0,0,5],
        [0,2,0,0,0,0,0,8,0]
    ]);

    println!("Problem");
    grid.print();

    solve(grid);
}

コードの全体像は冒頭のリポジトリに載せています。

実行イメージ

今回のプログラムを実行すると以下のような結果が得られます。

% cargo run --bin main

Problem
[0, 8, 0, 0, 0, 0, 0, 1, 0]
[1, 0, 0, 2, 0, 0, 9, 0, 0]
[0, 0, 7, 0, 0, 4, 0, 0, 3]
[3, 0, 0, 0, 1, 0, 0, 9, 0]
[0, 0, 0, 7, 0, 2, 0, 0, 0]
[0, 6, 0, 0, 8, 0, 0, 0, 4]
[9, 0, 0, 4, 0, 0, 1, 0, 0]
[0, 0, 4, 0, 0, 3, 0, 0, 5]
[0, 2, 0, 0, 0, 0, 0, 8, 0]
complete!
[4, 8, 5, 9, 3, 7, 6, 1, 2]
[1, 3, 6, 2, 5, 8, 9, 4, 7]
[2, 9, 7, 1, 6, 4, 8, 5, 3]
[3, 4, 2, 5, 1, 6, 7, 9, 8]
[8, 5, 9, 7, 4, 2, 3, 6, 1]
[7, 6, 1, 3, 8, 9, 5, 2, 4]
[9, 7, 8, 4, 2, 5, 1, 3, 6]
[6, 1, 4, 8, 9, 3, 2, 7, 5]
[5, 2, 3, 6, 7, 1, 4, 8, 9]

感想などのメモ

今回、Rustの勉強目的で数独を解くプログラムを書いてみました。久しぶりにガッツリ、アルゴリズムの実装を行って面白かったなというのが第一感想ですが、Rustの勉強にもちょうどよいボリュームと難易度だったと思います。

Rust自体の文法の難しさもありましたが、型あり言語ならではの VS Code の補完やサポートが強力なため、それらに助けられたなという印象もあります。

Rustはイテレータの扱いが独特で最初書き方がよく分からずに「？？」という状態でした。どんなメソッドがイテレータオブジェクトにあって、どんなメソッドがVectorにあるのかといったことがイマイチピンと来ていないので数をこなして慣れていきたいところです。

また、所有権周りもだいぶ苦しめられました。エラーメッセージで大体は何を修正すればいいかは教えてくれるのですが、いかんせん仕組みが難しいので、まだまだ慣れていかないとなと思います。

今回、データの中で None は扱いませんでした。最初は空セルを None で表現していたのですが、 Some ほにゃららと書いたり、 Option ほにゃららと書いたりと記述量が増していったので、 i32 型だけで完結するように途中で方針を変更しました。今回は扱うデータが少なくかつ明確なので、それでも十分だったかなと思うのですが、今後異なる対象のプログラムや規模の大きいプログラムを書く際は None をうまくハンドルすることが大事になりそうなので、そのあたりも学んでいきたいところです。