宇宙からの地球観測第６章 能動型センサ

宇宙からの地球観測　第6章の章末問題はついにきました。SAR Dataです。　去年の11月にSAR衛星を扱う会社に転職してからバイナリとしては頻繁に関わるようになりました。ただ、中身については理解できていません。気合い入れて課題に取り組みます。

問題6.1

SAR は相関処理で分解能を向上する。今，ALOS-2/PALSAR-2を想定して，分解能の向上率を計算しなさい。スラントレンジ長を 700km とする。

基本用語、公式の理解

アジマス、スラントレンジ、グラントレンジ

過去のまとめ 参照

帯域幅（BandWidth）と周波数（Frequency）は、信号処理や通信における基本的な概念であり、互いに関連していますが、異なる意味を持ちます。以下にそれぞれの定義と関係を詳しく説明します。

周波数（Frequency）

周波数（Frequency） は、波が1秒間に何回振動するかを示す指標です。単位はヘルツ（Hz）で、1 Hzは1秒間に1回の振動を意味します。例えば、音波や電磁波のような波動現象では、周波数が高いほど波が速く振動します。

• 例：音波の周波数
  • 低周波数（20 Hz - 200 Hz）：低音
  • 中周波数（200 Hz - 2000 Hz）：中音
  • 高周波数（2000 Hz - 20000 Hz）：高音

帯域幅（BandWidth）

帯域幅（BandWidth） は、特定の信号が占める周波数範囲の広さを示す指標です。帯域幅は、信号の周波数スペクトルにおいて、最低周波数から最高周波数までの差として定義されます。単位はヘルツ（Hz）です。

• 例：通信信号の帯域幅
  • 音声電話：約3.4 kHzの帯域幅（300 Hz - 3400 Hz）
  • テレビ信号：数MHzの帯域幅
  • Wi-Fi：数十MHzから数百MHzの帯域幅

周波数と帯域幅の関係

周波数と帯域幅は互いに関連していますが、異なる概念です。周波数は単一の波動の振動数を示し、帯域幅は特定の信号が占める周波数範囲の広さを示します。

• 単一周波数信号：単一の周波数で振動する純粋な音や波。帯域幅はゼロに近い。
  • 例：正弦波
• 複合信号：複数の周波数成分を含む信号。帯域幅が広くなる。
  • 例：音楽信号やテレビ信号

具体的な例

• 音楽信号
  音楽信号は、さまざまな周波数成分を含む複合信号です。ピアノの音は、低音から高音まで幅広い周波数範囲をカバーしています。この周波数範囲が音楽信号の帯域幅となります。

• 通信信号
  通信信号では、帯域幅はデータ伝送速度や信号品質に直接関係します。広い帯域幅を持つ信号は、高速なデータ伝送が可能であり、多くの情報を一度に送ることができます。

  • 音声電話：音声の基本的な周波数成分をカバーするために約3.4 kHzの帯域幅を使用します。
  • テレビ信号：映像と音声を高品質で伝送するために数MHzの帯域幅を使用します。
  • Wi-Fi：高速データ通信を可能にするために数十MHzから数百MHzの帯域幅を使用します。

相関処理

相互相関関数の概念

相互相関関数 $h(t)$ は、二つの信号間の類似性を時間的に評価するための手法です。これは信号 $f(t)$ と $g(t)$ の間で、一方の信号を時間的にシフトさせながら他方との類似度を計算することで、両信号がどのように関連しているかを示します。

式6.12

$$h(t) = \int_{-\frac{\tau}{2}}^{\frac{\tau}{2}} f(t') g^*(t + t') \, dt'$$

この式では、$f(t')$ は一定の時間関数で、$g(t + t')$ は $t$ によって時間的にシフトされた $g$ の関数,$\tau$はパルス幅、$*$は複素数共役を表しています。

式(6.12) の意味することは，このパルス時間内でf()とg()が同じ関数形（位相も含めて）を持つときのみ、瞬間的に大きな出力が得られ、それ以外では値は小さいかゼロである，また，参照信号と類似な成分だけを抽出できれば，分解能はかなり向上するということである。参照信号というとなにか特殊な印象を受けるが、そうではなく，一般には送信信号そのものである。今，参照信号として，送信信号にチャープ信号（パルス幅の間、周波数を線形に変化させて一定の帯域幅を持つように作成した信号，線形FM (frequency modulation） 信号とも呼ばれる）

なるほど、、　能動センサの場合、送信信号は自分で生成しているのでそれとの相関をみることでノイズを除去できるということですね。　単純で強力な数学処理ですね。

相互処理前後の分解能比較

記号について

1. レンジ相関（Range Resolution）:

   • SARが観測対象までの距離を測定する方向に関する分解能です。
   • $c$：光速（約300,000 km/s）。電磁波の速度であり、非常に高速です。
   • $\tau$ (タウ)：パルス幅。SARが送信する電波のパルスの持続時間を表します。
   • $B$ (ビー)：帯域幅。電波の周波数範囲を表します。広い帯域幅はより高い分解能を提供します。

2. アジマス相関（Azimuth Resolution）:

   • SARが観測対象の左右方向に関する分解能です。つまり、衛星の進行方向に垂直な方向。
   • $R$ (アール)：観測対象までの距離。SARと地表面との距離です。
   • $\lambda$ (ラムダ)：波長。SARが使用する電波の波長です。波長が短いほど高い分解能が得られます。
   • $L$ (エル)：アンテナの長さ。アンテナが長いほど、より高いアジマス分解能を達成できます。

数式、およびその説明

1. レンジ相関の分解能:

   • 処理前：$\frac{c\tau}{2}$
     • これは、SARの電波パルスの持続時間と光速によって決まる分解能です。
     • 例：5.25 km
   • 処理後：$\frac{c}{2B}$
     • 帯域幅の広さによって分解能が向上することを示します。
     • 例：0.01 km
   • 改善比率：$\tau B$
     • 分解能の向上の比率を示します。
     • 例：525倍

2. アジマス相関の分解能:

   • 処理前：$\frac{R\lambda}{L}$
     • これは観測対象までの距離、波長、およびアンテナの長さによって決まる分解能です。
     • 例：14.1 km
   • 処理後：$\frac{L}{2}$
     • アンテナの長さによって分解能が向上することを示します。
     • 例：0.00596 km
   • 改善比率：$\frac{2R\lambda}{L^2}$
     • 分解能の向上の比率を示します。
     • 例：2366倍

要約

SARの分解能は、レンジ方向とアジマス方向でそれぞれ異なる方法で決定されます。レンジ方向の分解能は、電波パルスの持続時間と帯域幅に依存し、アジマス方向の分解能は観測距離、波長、アンテナの長さに依存します。適切な信号処理を行うことで、これらの分解能を大幅に向上させることができます。

回答6.1

本文に下記の表がありますので上記の計算に入れ込むことで結果が出ます

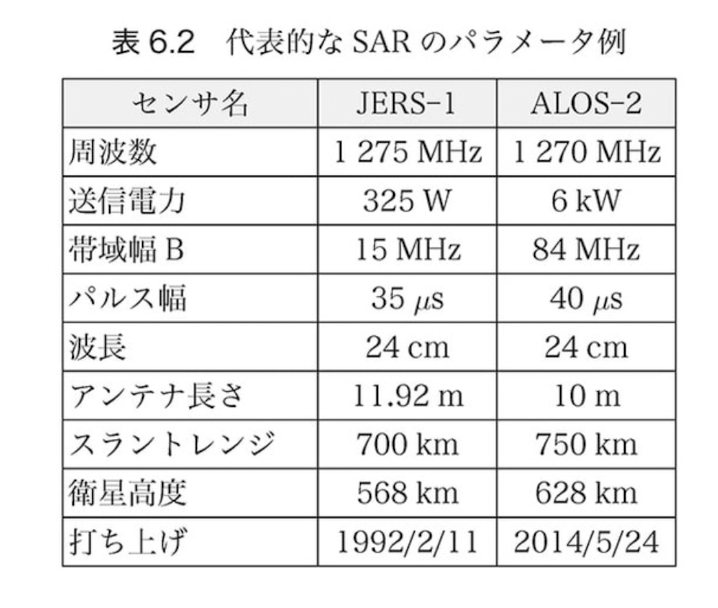
# 定数の定義
c = 3 * 10**8  # 光速 [m/s]
tau = 40e-6  # パルス幅 [秒]
B = 84e6  # 帯域幅 [Hz]
R = 700e3  # 観測対象までの距離 [m]
lambda_ = 0.236  # 波長 [m]
L = 10  # アンテナの長さ [m]

# レンジ相関の処理前、処理後の分解能と改善率の計算
range_resolution_before = (c * tau) / 2 / 1000  # kmに変換
range_resolution_after = (c / (2 * B)) / 1000  # kmに変換
range_improvement_ratio = tau * B

# アジマス相関の処理前、処理後の分解能と改善率の計算
azimuth_resolution_before = (R * lambda_) / L / 1000  # kmに変換
azimuth_resolution_after = L / 2 / 1000  # kmに変換
azimuth_improvement_ratio = (2 * R * lambda_) / (L**2)

# 結果を出力
print(f"レンジ相関の処理前の分解能: {range_resolution_before:.2f} km")
print(f"レンジ相関の処理後の分解能: {range_resolution_after:.5f} km")
print(f"レンジ相関の改善率: {range_improvement_ratio:.0f}")

print(f"アジマス相関の処理前の分解能: {azimuth_resolution_before:.2f} km")
print(f"アジマス相関の処理後の分解能: {azimuth_resolution_after:.5f} km")
print(f"アジマス相関の改善率: {azimuth_improvement_ratio:.0f}")
---
レンジ相関の処理前の分解能: 6.00 km
レンジ相関の処理後の分解能: 0.00179 km
レンジ相関の改善率: 3360
アジマス相関の処理前の分解能: 16.52 km
アジマス相関の処理後の分解能: 0.00500 km
アジマス相関の改善率: 3304

すごい改善率ですね、　数学が魔法のように見えます。
本書の実際の画像の例で見ると　相関処理前の画像は 分解能が悪くぼやけて地上の様子が全く判別できませんが、それが相関処理を行うことで、解像度数メートルのなりくっきり地表の様子がみえるようになります。（衛星画像はくっきり見えるのが当たり前と思っていた自分を悔い改めました。）

問題6.2

JERS-1と PAISAR-2のチャープ率とドップラーチャープ率を計算しなさい。速度は7km/s，ro=700kmとしなさい。

基本用語、公式の理解

チャープ率とは？

チャープ（Chirp） とは、時間とともに周波数が変化する信号のことを指します。具体的には、送信される信号の周波数が一定の時間範囲内で低い周波数から高い周波数、またはその逆に変化します。このような信号は、レーダーや音響測定などで使われます。

チャープ率 は、この周波数変化の速度を示す指標です。例えば、1秒間に周波数が1 kHzから5 kHzに増加するチャープ信号があれば、チャープ率は（5 kHz - 1 kHz）/ 1秒 = 4 kHz/秒となります。このチャープ率が高いほど、周波数が速く変化することを意味します。

チャープ率（chirp rate）は、信号の周波数が時間とともにどれだけ変化するかを示す指標です。チャープ信号では、周波数が線形に変化するため、この変化率を定量的に表すことができます。チャープ信号の設計や解析では、帯域幅とパルス幅が重要な役割を果たします。

チャープ率の定義

チャープ率 $\gamma$ は、単位時間あたりの周波数変化量を表します。チャープ信号において、信号の周波数が時間 $t$ に対して線形に変化すると仮定すると、その式は次のようになります：

$f(t) = f_0 + \gamma t$

ここで、$f(t)$ は時刻 $t$ における瞬時周波数、$f_0$ は初期周波数、$\gamma$ はチャープ率です。

帯域幅とパルス幅の関係

チャープ信号の設計では、信号の周波数変化の範囲（帯域幅）と信号が持続する時間（パルス幅）が重要です。具体的には、チャープ信号が開始から終了までにどれだけの周波数範囲をカバーするかが帯域幅 $B$ で表され、信号が持続する時間がパルス幅 $\tau$ で表されます。

チャープ率の計算

チャープ率 $\gamma$ は、信号の帯域幅 $B$ とパルス幅 $\tau$ を用いて次のように計算されます：

$\gamma = \frac{B}{\tau}$

これは、次のようにして導かれます：

1. 周波数変化量：信号がカバーする周波数範囲は帯域幅 $B$ によって表されます。これは、信号が開始時の周波数から終了時の周波数までの変化量です。

2. 時間変化量：信号がその周波数変化を達成するまでの時間はパルス幅 $\tau$ によって表されます。

3. チャープ率：チャープ率は、周波数変化量を時間変化量で割ったもので、単位時間あたりの周波数変化量を示します。したがって、

$\gamma = \frac{\text{周波数変化量}}{\text{時間変化量}} = \frac{B}{\tau}$

• 例

例えば、帯域幅 $B = 100$ MHz のチャープ信号がパルス幅 $\tau = 10$ μs で送信される場合、チャープ率は次のように計算されます：

$\gamma = \frac{100 \times 10^6 \text{ Hz}}{10 \times 10^{-6} \text{ s}} = 10^{13} \text{ Hz/s}$

このチャープ率は、信号の周波数が時間とともにどれだけ急速に変化するかを示しています。

ドップラーチャープ率とは？

ドップラーチャープ率 は、ドップラー効果とチャープ信号を組み合わせた概念です。ドップラー効果は、観測者が送信機に対して動いているときに、観測される周波数が変化する現象です。例えば、救急車のサイレンの音が近づくと高くなり、遠ざかると低くなるのはドップラー効果の一例です。

レーダーシステムでは、対象物が動いているとき、その運動によって反射される信号の周波数が変化します。これをドップラー周波数偏移（ドップラーシフト）と呼びます。

ドップラーチャープ率 は、レーダー信号が対象物の速度によってどれだけの周波数変化が生じるかを示します。これは対象物の速度や方向によって決まります。具体的には、対象物がレーダーに向かって近づくときには周波数が高くなり、遠ざかるときには低くなります。この周波数変化の速度がドップラーチャープ率です。

本文 式6.7の解説

ドップラー周波数計測では、対象物が動いている場合、反射される信号にドップラー効果が現れることを示しています。式6.7は、ドップラー周波数 $f_d$ を計算するためのもので、次のように表されます：

$f_d = \frac{2}{\lambda} u \cdot \left( \frac{\vec{r_s} - \vec{r_p}}{|\vec{r_s} - \vec{r_p}|} \right) = \frac{2}{\lambda} |u| \cos \theta$

ここで、

• $\lambda$ は信号の波長。
• $u$ は人工衛星の速度ベクトル。
• $\vec{r_s}$ は衛星の位置ベクトル。
• $\vec{r_p}$ は地上の観測点の位置ベクトル。
• $\theta$ は衛星進行方向と地表点との間の角度。

この式は、対象物の速度や方向によって反射信号の周波数がどのように変化するかを示しています。

距離の関数

衛星が速度 $V$ で等速直線運動を行うとき、衛星と対象点との距離（スラントレンジ）は次のように表されます：

$r(T) = \sqrt{r_0^2 + (VT)^2} \approx r_0 + \frac{V^2}{2r_0} T^2$

ここで、

• $r_0$ は衛星と対象物の最近接距離
• $T$ は時間
• $V$ は衛星の速度

この式は、地面までの距離が時間の二次関数であることを示し、地面でカーブを描くことになります。これをカーパチャーといいます。

ドップラー周波数

この距離関数を受信信号に代入すると、ドップラー周波数の時間変化率（ドップラーチャープ率）は次のように表されます：

(本文式6.15)$f_{DD} = \frac{1}{2\pi} \frac{\partial^2 \phi}{\partial T^2} = -\frac{2 V^2}{\lambda r_0}$

ドップラーチャープ率の詳細

• ドップラー周波数 $f_D$ は、衛星の移動により生じる信号の周波数変化を示します。
• ドップラーチャープ率 $f_{DD}$ は、このドップラー周波数の時間変化率を示します。これは、衛星の速度 $V$ と最近接距離 $r_0$ に依存し、衛星の運動が周波数に与える影響を定量的に示します。

本文

SARの処理で大変なのはアジマス方向の参照信号を正確に求めることであり、ドップラーチャープ率の計算には1/10000の精度が求められる

この文章の意味も問題6.1の相関処理で少しでも値がことなるとずれてしまうところから考えても納得できました。

回答6.2

import numpy as np

# チャープ率を計算する関数
def calculate_chirp_rate(bandwidth, pulse_width):
    """
    チャープ率を計算します。
    
    Args:
    bandwidth (float): 帯域幅 (MHz)
    pulse_width (float): パルス幅 (秒)
    
    Returns:
    float: チャープ率 (Hz/s)
    """
    bandwidth_hz = bandwidth * 1e6  # MHzをHzに変換
    chirp_rate = bandwidth_hz / pulse_width  # チャープ率の計算
    return chirp_rate

# ドップラーチャープ率を計算する関数
def calculate_doppler_chirp_rate(velocity, initial_distance, wavelength):
    """
    ドップラーチャープ率を計算します。
    
    Args:
    velocity (float): 物体の速度 (m/s)
    initial_distance (float): 物体との初期距離 (m)
    wavelength (float): 波長 (m)
    
    Returns:
    float: ドップラーチャープ率 (Hz/s)
    """
    doppler_chirp_rate = -(2 * velocity**2) / (wavelength * initial_distance)
    return doppler_chirp_rate

# JERS-1パラメータの設定
bandwidth = 15.0  # MHz
pulse_width = 35e-6  # 秒
velocity = 7000  # m/s (衛星の典型的な速度)
initial_distance = 700e3  # m (衛星と地表との距離)
wavelength = 0.024  # m (Xバンドレーダーの典型的な波長)

# 計算
chirp_rate = calculate_chirp_rate(bandwidth, pulse_width)
doppler_chirp_rate = calculate_doppler_chirp_rate(velocity, initial_distance, wavelength)

# 結果の出力
print(f"チャープ率: {chirp_rate:.2e} Hz/s")
print(f"ドップラーチャープ率: {doppler_chirp_rate:.2e} Hz/s")
---
チャープ率: 4.29e+11 Hz/s
ドップラーチャープ率: -5.83e+03 Hz/s

最初問題分にあるPALSARのパラメータがないじゃないかと探しましたが、
PALSARはALOS2プロジェクトで搭載されたセンサーのことでした。
なので6.1 でも表示した表に記載してありました。

問題6.3

JERS-1の地上における電界強度，人工衛星で受信する受信電力を求めなさい。r=700km, G=8100,$\sigma=1000m^2$, $P_t=325W$とする。

基本公式の理解

電磁波の放射パターンとアンテナの利得に関する基本的な概念

電磁波の放射と球面波

送信アンテナから放射された電磁波は、理想的には全方向に均等に広がると仮定されます。これは、電磁波が球面波として広がることを意味します。球面波の面積は、放射源からの距離 $r$ に対して球の表面積で表されます。この表面積は次の式で表されます：

$$A = 4 \pi r^2$$

アンテナの利得と受信電力

アンテナの利得 $G$ は、アンテナが特定の方向にどれだけ効率的に電力を放射または受信するかを示す指標です。アンテナの利得は、理想的な等方性アンテナ（全方向に均等に放射するアンテナ）に対して相対的に測定されます。

レーダー方程式1. 地上における電界強度

レーダー方程式では、送信電力が球面波として広がることを考慮し、受信アンテナがその電力の一部を受信することを計算します。具体的には、送信電力が距離 $r$ に応じて広がるため、受信電力は距離の二乗に反比例します。この広がりを表すために、球面の表面積 $4πr^2$ が使用されます。

$$P_r = \frac{P_t G}{4 \pi r^2}$$

ここで、各項の意味は次の通りです：

• $P_r$ は受信電力
• $P_t$ は送信電力
• $G$ はアンテナ利得
• $r$ は送信源からの距離
• $\pi$ は円周率

この式は、送信された電波が距離 $r$ だけ進んだ後に、受信アンテナが受け取る電力 $P_r$ を示しています。この電力は、送信電力とアンテナ利得に比例し、衛星からの距離を半径とした球面積に反比例します。

レーダー方程式2. 衛星の受信電力

$$P_r = \frac{P_t G}{4 \pi r^2} \sigma \frac{1}{4 \pi r^2} \frac{G \lambda^2}{4 \pi}$$

この式は、送信電力とアンテナ利得、距離、散乱断面積、波長に基づいて、受信アンテナが受け取る電力を計算します。以下は各項の説明です：

• $P_t$ は送信電力
• $G$ はアンテナ利得
• $r$ は送信源からの距離
• $\sigma$ は散乱断面積
• $\lambda$ はレーダ波長

式の意味：

• 送信電力 ($P_t$): 衛星から発信される電力。
• アンテナ利得 ($G$): アンテナの指向性を示し、方向性の強さを表します。
• 距離 ($r$): 衛星から地上までの距離。距離が遠くなると電力は減少します。
• 散乱断面積 ($\sigma$): 地上の目標物が電波をどれだけ反射するかを示す指標。
• 波長 ($\lambda$): 送信される電波の波長。

メタファーでの理解

地上における電界強度

懐中電灯の例を考えてみましょう。懐中電灯が強く光を放つと、その光は遠くまで届きます。しかし、懐中電灯から遠ざかるにつれて、光は広がり、弱くなります。この光の強さを電界強度と考えることができます。

$$P_r = \frac{P_t G}{4 \pi r^2}$$

これは、懐中電灯（送信電力 $P_t$）がどれだけ強く光るか（アンテナ利得 $G$）と、どれだけ離れているか（距離 $r$）に基づいて、どれくらいの光（電力）が届くかを示しています。

受信電力

電波が地上に到達したとき、それがどれだけ反射されて戻ってくるかを計算するためには、目標物の反射能力（散乱断面積 $\sigma$）と電波の性質（波長 $\lambda$）も考慮します。

$$P_r = \frac{P_t G}{4 \pi r^2} \sigma \frac{1}{4 \pi r^2} \frac{G \lambda^2}{4 \pi}$$

これは、懐中電灯の光が鏡（散乱断面積 $\sigma$）に当たって反射し、再び戻ってくる光の強さを示しています。鏡の大きさや質（波長 $\lambda$）によって、反射される光の強さが変わります。

これらの式は、電磁波がどのように伝播し、どのように受信されるかを理解するための基本的なものです。

受信電力の最後の項「$\frac{G \lambda^2}{4\pi}$」について

$$\frac{G \lambda^2}{4\pi}$$

この項は、アンテナの利得 $G$、波長 $\lambda$、そして $4\pi$ で構成されています。それぞれの意味を以下に説明します：

アンテナ利得 $G$

アンテナ利得 $G$ は、アンテナが特定の方向にどれだけ効率よく電波を送受信できるかを示す指標です。利得が高いアンテナは、狭いビームで強い信号を送受信できます。これは、アンテナの指向性を反映しています。

波長 $\lambda$

波長 $\lambda$ は、電波の1周期の長さを示します。波長が長いほど、電波は遠くまで届きやすくなりますが、解像度が低くなります。波長が短いと解像度は高くなりますが、減衰が早くなります。

$4\pi$

この項の $4\pi$ は、球面の表面積を表しています。これは、電波が全方向に均等に広がることを考慮したものです。具体的には、電波が球面波として広がる際の広がり具合を表しています。

項の役割

$\frac{G \lambda^2}{4\pi}$ は、電波がアンテナからどのように放射されるか、そして受信アンテナがどれだけ効率よくその電波を受け取れるかを定量的に示しています。この項は、以下の点で重要です：

1. アンテナ性能の評価: アンテナの利得 $G$ が高いと、この項の値も大きくなります。これは、より強い信号が送受信されることを意味します。
2. 波長の影響: 波長 $\lambda$ が長いと、この項の値も大きくなります。これは、長波長の電波が遠くまで届きやすく、減衰が少ないことを示しています。
3. 球面波の広がり: $4\pi$ は、電波が全方向に広がる際のエネルギーの分布を表しており、実際の電波伝播を正確にモデル化するために必要です。

回答6.3

上記の　地上の電界強度、衛星の受信電力の公式をプログラムにして、本文のパラメータを設定して計算します。

import math

# Given values
r = 700e3  # distance in meters
G = 8100  # antenna gain
sigma = 1000  # radar cross-section in square meters
Pt = 325  # transmitted power in watts
lambda_ = 0.000236  # wavelength in killo meters

# Constants
pi = math.pi

# Electric field strength at the ground (Pr)
Pr_ground = Pt * G / (4 * pi * r**2)

# Received power by the satellite
Pr_satellite = (Pt * G / (4 * pi * r**2)) * sigma * (1 / (4 * pi * r**2)) * (G * lambda_**2 / (4 * pi))


print(f"Ground:{Pr_ground:.3e}, Sat:{Pr_satellite:.3e}")
--
Ground:4.275e-07, Sat:2.493e-21

感動です。数式をみて、球面がぶつかって球面がかえってくるというイメージが持てるようになりました！！