そろそろShaderをやるパート31 内積を使う
そろそろShaderをやります
そろそろShaderをやります。そろそろShaderをやりたいからです。
パート100までダラダラ頑張ります。10年かかってもいいのでやります。
100記事分くらい学べば私レベルの初心者でもまあまあ理解できるかなと思っています。
という感じでやってます。
※初心者がメモレベルで記録するので
技術記事としてはお力になれないかもしれません。
下準備
下記参考
そろそろShaderをやるパート1 Unite 2017の動画を見る(基礎知識~フラグメントシェーダーで色を変える)
デモ
下記画像は単位ベクトル同士のベクトルの内積で行ったグラデーションです。
もう少し正確に言うと、正規化された各ピクセルのワールド座標と座標(0,1)の位置ベクトルの内積を利用しています。内積結果をLerpの補間値として利用しています。

下記画像は単位ベクトル同士ではない内積で行ったグラデーションです。
もう少し正確に言うと、正規化していない各ピクセルのワールド座標と座標(0,1)の位置ベクトルの内積を利用しています。こちらも内積結果をLerpの補間値として利用しています。

Shaderサンプル
Shader "Custom/Dot"
{
Properties
{
_Color1("Color 1",Color) = (0,0,0,1)
_Color2("Color 2",Color) = (1,1,1,1)
}
SubShader
{
Tags
{
"RenderType"="Opaque"
}
Pass
{
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
#include "UnityCG.cginc"
//頂点シェーダーに渡ってくる頂点データ
struct appdata
{
float4 vertex : POSITION;
};
//フラグメントシェーダーへ渡すデータ
struct v2f
{
float4 vertex : SV_POSITION;
float3 worldPos : WORLD_POS;
};
float4 _Color1;
float4 _Color2;
//頂点シェーダー
v2f vert(appdata v)
{
v2f o;
//unity_ObjectToWorld × 頂点座標(v.vertex) = 描画しようとしてるピクセルのワールド座標 らしい
//mulは行列の掛け算をやってくれる関数
o.worldPos = mul(unity_ObjectToWorld, v.vertex).xyz;
o.vertex = UnityObjectToClipPos(v.vertex); //3D空間座標→スクリーン座標変換
return o;
}
//フラグメントシェーダー
fixed4 frag(v2f i) : SV_Target
{
//各ピクセルのワールド座標の位置ベクトルを正規化していないパターン
//float interpolation = dot(i.worldPos,float2(0,1));
//斜め方向のベクトルを利用
//float interpolation = dot(i.worldPos,normalize(float2(1,1))));
//単位ベクトル同士
float interpolation = dot(normalize(i.worldPos),float2(0,1));
fixed4 col = lerp(_Color1,_Color2, interpolation);
return col;
}
ENDCG
}
}
}
内積はdotにより計算することが可能です。
内積
上記の式を余弦定理を利用して表すと下記のようになります。
ベクトルの絶対値はスカラーと言って、
ベクトルの向きなどは含まれない単純な大きさを意味します
計算結果をxとした時、その値は
1×1×cosθなので、単純にcosθの取り得る値が
ここで再度、内積を使ったグラデーションを見ていきます。
Planeをxy平面上であると仮定して考えます。
Unity上で原点(0,0,0)に配置し、xy方向のスケールを2にすることで仮想的にxy平面(
下記図において、青の矢印は"任意の方向に存在するピクセルの位置ベクトル"を正規化したベクトル(スカラー1のベクトル)とします。
赤の矢印は座標(0,1)の位置ベクトルであり、スカラー1のベクトルです。
それぞれ、青を
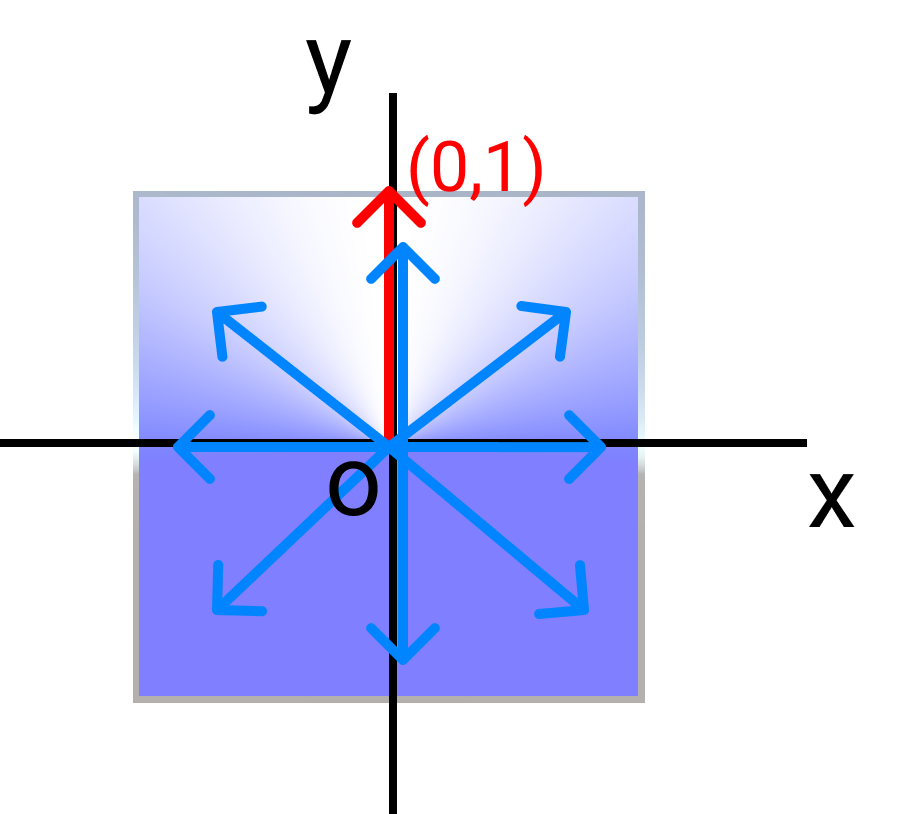
次に
緑色の数字が内積の結果
先述の通り、
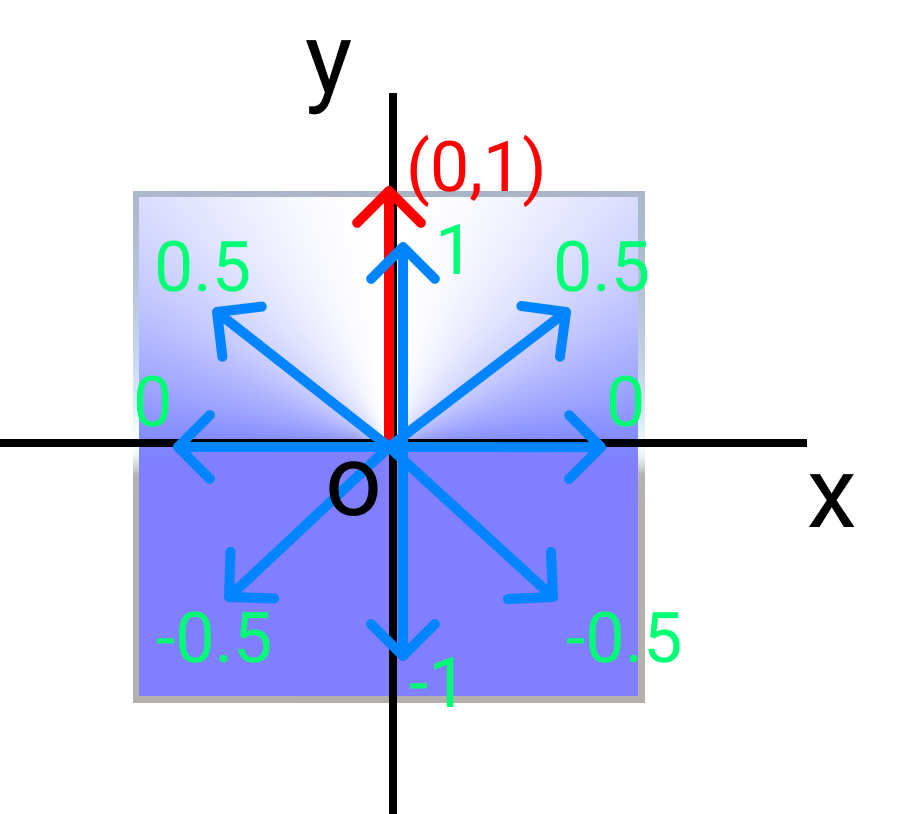
この内積の結果

この処理を担うコードは下記部分になります。
//フラグメントシェーダー
fixed4 frag(v2f i) : SV_Target
{
float interpolation = dot(normalize(i.worldPos),float2(0,1));
fixed4 col = lerp(_Color1,_Color2, interpolation);
return col;
}
次に単位ベクトル同士ではない場合を見ていきます。
任意のピクセルの位置ベクトルを正規化しない場合、
下記式に代入して見ればわかりますが、内積の計算結果は
試しに先ほどの(0,1)のベクトルはそのままに、任意のピクセルの座標を(x,y)とした場合を計算式に当てはめてみます。
それぞれ座標(0,1)の位置ベクトルを
内積の結果は任意のピクセルの座標のy座標となりました。
図示すると下記のように、ピクセルのy座標が増えれば増えるほど内積の返す値が増える計算結果となります。
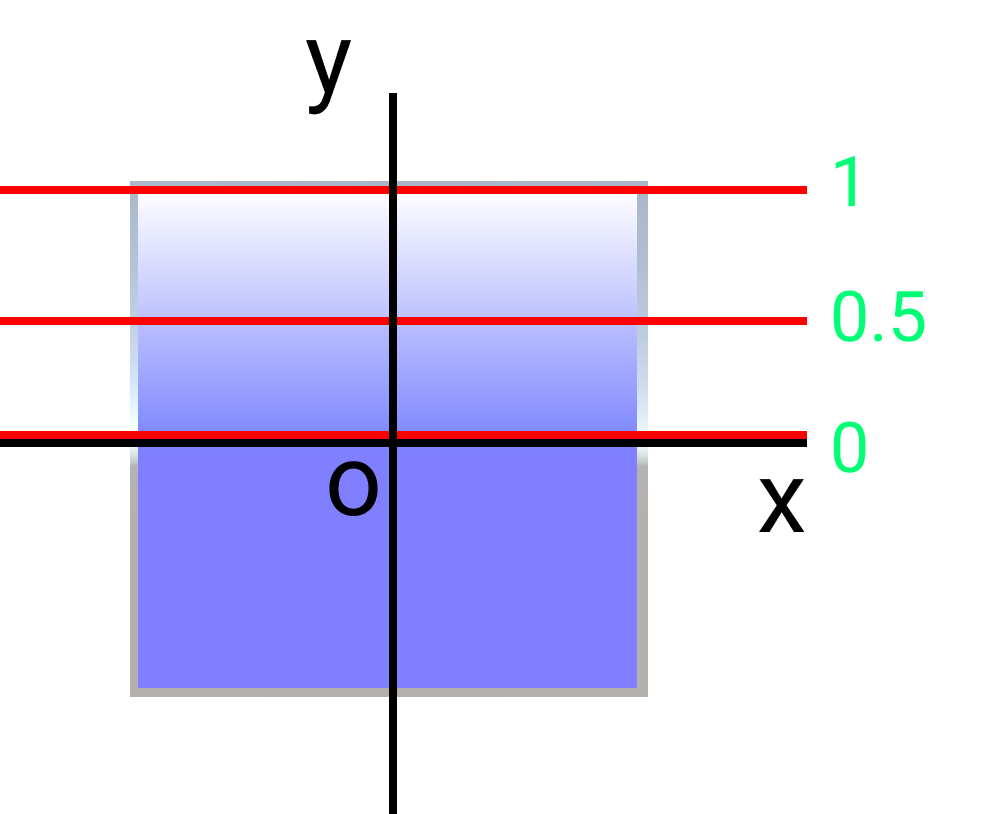
この内積の結果をLerp(線形補間)の補間値として利用することで任意の方向へのグラデーションとなります。
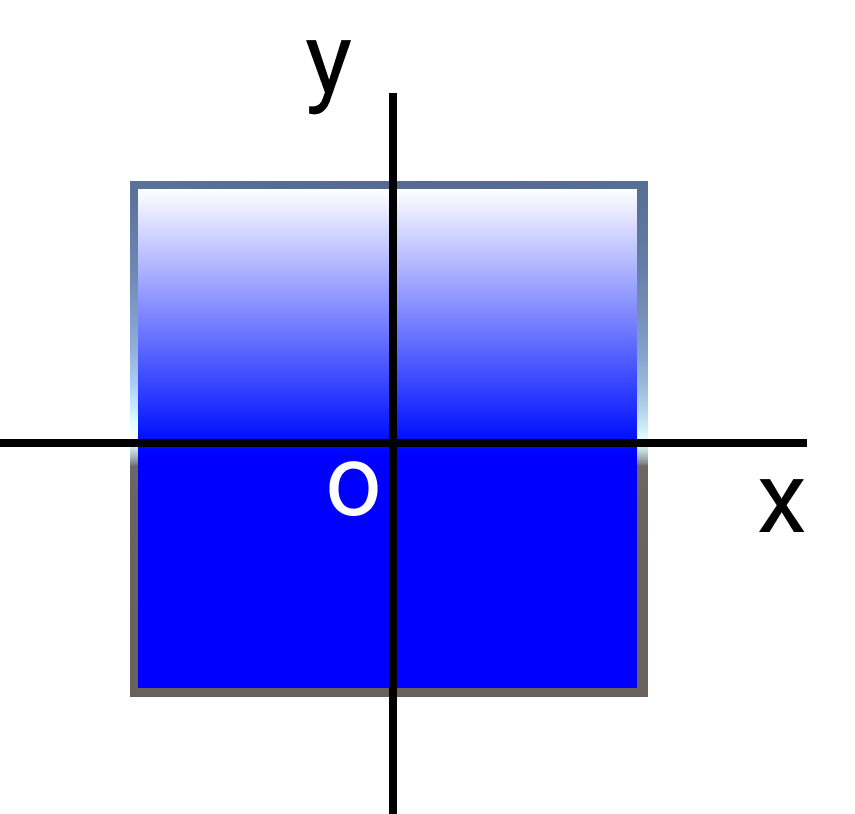
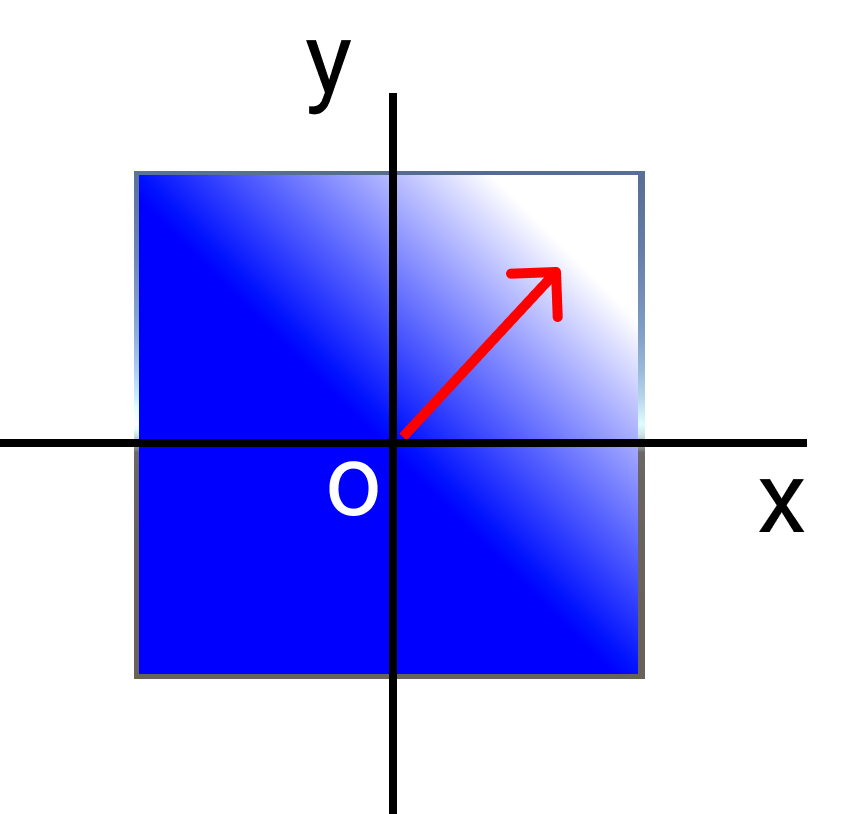
別方向のグラデーションの例として、
座標(1,1)の位置ベクトルを正規化し、計算に利用した場合が下記画像です。
コードに落とし込むと下記です。
//フラグメントシェーダー
fixed4 frag(v2f i) : SV_Target
{
float interpolation = dot(i.worldPos,normalize(float2(1,1)));
fixed4 col = lerp(_Color1,_Color2, interpolation);
return col;
}
参考リンク
3Dスキャンライン表現
【シェーダーグラフメモ その56】内積を使って任意方向のグラデーションを作る
数学:内積ってなんぞ? その2(角度とCG編)
Discussion