はじめに

この記事は https://zenn.dev/kawaxumax/articles/4c930efd511f75 の続編となります。
時系列データを扱うのに適しているARIMAモデルについて概要を説明し、実際に仮想通貨の相場データに適用して、価格を推定してみようと思います。

参考文献

Wikipedia - 自己回帰和分移動平均モデル
 新手法例時系列分析（ARIMAモデル）の機能とその活用（株式会社日本科学技術研修所王克義）
sktimeで時系列データを予測してみた
 【時系列解析入門】2. ARモデル
 【時系列分析の基本】定常性とホワイトノイズ
 時系列分析の概要
 時系列データに対する3つの特徴把握方法

展望

深層学習RNNモデルの構築

おるとろ

時系列データ

等間隔で観測された一連のデータのことを時系列データといいます。例としては気温や株価が挙げられます。時系列データには時間に関連した変遷、周期性の解析などの特有の解析手法があります。

今回は時系列データ解析の手法をいくつか紹介し、最後に、その一つであるARIMAモデルを仮想通貨の価格推定に応用してみたいと思います。

時系列データの変動要因

時系列データは以下のような変動要因があり、それぞれの要因をどの程度考慮に入れるか、によっていくつか分析モデルが異なってきます。

自己相関
傾向変動(トレンド)
周期変動
季節性変動(一年や四季を周期として変動する)
不規則変動(外因性変動)
ノイズ

参考文献

時系列データモデル

時系列分析には、いろいろなモデルが存在します。今回はその中でもARIMAモデル周辺のモデルを取り上げます。

ARモデル
AR（自己回帰）モデル、自己回帰モデルと呼ばれ、「過去の自分のデータ」を説明変数とします。定常性を前提とします。
MAモデル
MAモデルは移動平均モデルと言われ、為替データなどのテクニカル指標で使われるものと同じです。定常性を前提とします。
ARMAモデル
ARMAモデルはARモデルとMAモデルを組み合わせたモデルです。定常性を前提とします。
ARIMAモデル
ARIMA（自己回帰和分移動平均）モデルを用いた時系列分析は、データ系列のある点とその直近時点の値との関係性を分析し、それらの関係性が将来も保存されるという仮定を置いて予測する手法です。定常性がない場合に有効です。

おるとろ

使えそうなフレームワーク

おるとろ

統計値

共分散

共分散は対応する二つのデータの関係を表す値です。偏差を掛け合わせたものの平均のことを指します。データ集合 $X$ と $Y$ があり、それぞれの各データを $x_t$ , $y_t$ 、それぞれの平均を $\bar{x}$ 、 $\bar{y}$ としたとき、共分散 $Cov(X,Y)$ は以下のように表されます。

\begin{aligned} Cov(X,Y) &= \frac{1}{n}\sum^{n}_{t=1}(x_{t} - \bar{x})(y_{t} - \bar{y}) \\ &= \frac{1}{n}\sum^{n}_{t=1}x_{t}y_{t} - \bar{x}\bar{y} \end{aligned}

自己共分散

自己共分散は、時間をずらした自分自身との共分散です。ある時刻 $t$ と時間を $k$ だけずらした時刻 $t-k$ を対応させると以下のようになります。

\begin{aligned} Cov(X_t,X_{t-k}) &= \frac{1}{n}\sum^{n}_{t=1}(x_{t} - \bar{x})(x_{t-k} - \bar{x}) \\ &= \frac{1}{n}\sum^{n}_{t=1}x_{t}x_{t-k} - \bar{x}^2 \end{aligned}

自己相関

自己相関は自己共分散を分散で割ったもの。周期パターンの分析などに使われます。自己相関 $R$ は時刻 $t$ とずらし幅 $k$ 、分散 $σ^2$ を用いて以下のような式で表せます。

\begin{aligned} R(X_t,X_{t-k}) &= \frac{\frac{1}{n}\sum^{n}_{t=1}(x_{t} - \bar{x})(x_{t-k} - \bar{x})}{σ^2} \end{aligned}

おるとろ

定常性

時間によらず期待値、自己共分散が一定であるような時系列データの性質を定常性といいます。また、定常性を持つ確率過程のことを定常過程と呼びます。

ホワイトノイズ

自己共分散が $0$ 、期待値が $0$ 、分散が $σ^2$ であるような時系列データをホワイトノイズといいます。

おるとろ

ARモデル

おるとろ

環境構築

sktimeというパッケージを使ってみたいと思います。

mkdir time_series # 適切な場所で作業用フォルダを作成
cd time_series # 移動
pipenv --python 3.9 # pythonの環境を初期化する。sktimeは3.9系で使えます。


# scikit-learn と関連パッケージをインストールする
# sktimeが今回主に使いたい時系列解析のパッケージ
# pmdarimaがarima分析モジュールが依存しているパッケージ
pipenv install scikit-learn numpy matplotlib sktime pmdarima

pipenv install --dev jupyter # jupyterというグラフィカルな対話式実行環境をインストールする
code . # VScodeで開く

sktimeでARモデルを組む

Non-seasonal ARIMA models are generally denoted ARIMA(p,d,q) where parameters p, d, and q are non-negative integers, p is the order (number of time lags) of the autoregressive model, d is the degree of differencing (the number of times the data have had past values subtracted), and q is the order of the moving-average model. Seasonal ARIMA models are usually denoted ARIMA(p,d,q)(P,D,Q)m, where m refers to the number of periods in each season, and the uppercase P, D, Q refer to the autoregressive, differencing, and moving average terms for the seasonal part of the ARIMA model.

非季節性ARIMAモデルは、一般にARIMA(p,d,q)と表記され、パラメータp、d、qは非負の整数、pは自己回帰モデルの次数（タイムラグの数）、dは差分の程度（データの過去値を何回引いたか）、qは移動平均モデルの次数である。

また、季節性のARIMAモデルも扱うことができてARIMA(p,d,q)(P,D,Q)mと表現します。ここで、mは各季節の期間数、大文字のP,D,QはARIMAモデルの季節部分の自己回帰項、差分項、移動平均項を表しています。

When two out of the three terms are zeros, the model may be referred to based on the non-zero parameter, dropping “AR”, “I” or “MA” from the acronym describing the model. For example, ARIMA(1,0,0) is AR(1), ARIMA(0,1,0) is I(1), and ARIMA(0,0,1) is MA(1). [1] See notes for more practical information on the ARIMA class.

3つの項のうち2つが0である場合、モデルを説明する頭字語から「AR」「I」「MA」を削除し、0でないパラメータに基づいてモデルを参照することができる。例えば、ARIMA(1,0,0) は AR(1), ARIMA(0,1,0) は I(1), ARIMA(0,0,1) は MA(1) である。[1] ARIMAクラスの実用的な情報は注釈を参照してください。

参考

おるとろ

sktimeを使ってみる

pipenv run jupyter notebook # jupyter notebookのサーバーを立ち上げる

おるとろ

データの取得

最初にARモデルを試します。Sktimeにはサンプルのデータセットが含まれていますので、そちらをつかってみましょう。

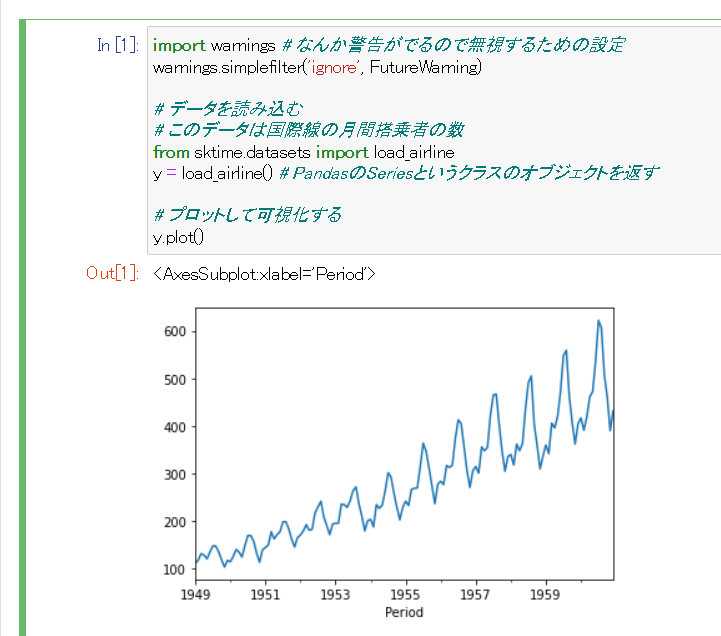
# データを読み込む
# このデータは国際線の月間搭乗者の数
from sktime.datasets import load_airline
y = load_airline() # PandasのSeriesというクラスのオブジェクトを返す

# プロットして可視化する
y.plot()

おるとろ

ARIMAモデルの作成

それではsktimeを用いて時系列解析モデルを作成していきましょう。
sktimeのsktime.forecasting.arimaモジュールのARIMAという関数を用いてモデルを構築することができます。
引数のorder=(a,b,c)のそれぞれはAR、I、MAに対応しています。例えばorder=(1,0,0)とすると、1次のARモデルを構築することができます。また、order=(0,0,4)では4次のMAモデルを構築することになります。
また、引数のseasonal_order=(d,e,f,g)は季節性を導入する値となっています。

from sktime.forecasting.arima import ARIMA
forecaster = ARIMA(order=(1, 1, 0), seasonal_order=(0, 1, 0, 12), suppress_warnings=True)
forecaster.fit(y)
forecaster.summary()

# predictメソッドで予測する
# fhはfuture horizonの略で、入力データの続きの部分をあらわす。
# fh=[1,2,3]では、未来3か月分の予測データを出力するということ。
y_pred = forecaster.predict(fh=[1,2,3]) # pandas.core.series.Series を返す
y_pred.plot()

参考文献

おるとろ

参考文献

TODO:

ARIMAの依存パッケージを入れたのでARとIとMAをそれぞれ試す

それぞれ試す分にはいいんだけど、今回のデータのair_passengerは定常性がないのでARとMRには適していない。

おるとろ

SARIMAモデルらしい

import warnings # なんか警告がでるので無視するための設定
warnings.simplefilter('ignore', FutureWarning)

# データを読み込む
# このデータは国際線の月間搭乗者の数
from sktime.datasets import load_airline
y = load_airline() # PandasのSeriesというクラスのオブジェクトを返す

# プロットして可視化する
y.plot()

# 精度の確認用に、データを半分に分ける
half_len = int(y.count()/2)
half_y = y[0:half_len]

from sktime.forecasting.arima import ARIMA
forecaster = ARIMA(order=(1, 1, 0), seasonal_order=(0, 1, 0, 12), suppress_warnings=True)
forecaster.fit(half_y)
forecaster.summary() # モデルの説明を表示する

元データと予測データを描画する

y_pred = forecaster.predict(fh=list(range(1, half_len)))

# 元データのグラフを表示する
ax1 = y.plot()
# 予測データのグラフを表示する
y_pred.plot(ax = ax1)

おるとろ

定常性のある時系列データセットが欲しい

おるとろ

sktimeで変動成分分解

# Deseason
from sktime.transformations.series.detrend import Deseasonalizer
from sktime.datasets import load_airline
y = load_airline()
transformer = Deseasonalizer()
y_hat = transformer.fit_transform(y)

# Detrend
from sktime.transformations.series.detrend import Detrender
from sktime.forecasting.trend import PolynomialTrendForecaster
from sktime.datasets import load_airline
y = load_airline()
transformer = Detrender(forecaster=PolynomialTrendForecaster(degree=1))
y_hat = transformer.fit_transform(y)

おるとろ

TODO

y_train, y_test = temporal_train_test_split(y) 訓練用のデータとテスト用のデータを分ける
mean_absolute_percentage_error(y_test, y_pred) 精度の平均値