Pythonで機械学習に入門して仮想通貨の価格を推定する-線形回帰編-
はじめに
この記事ではPythonの機械学習パッケージであるscikit-learnを用いて機械学習に入門しようと思います。
scikit-learnの使い方の説明を主とし、簡単な統計用語の解説を交えつつ、最後に実践として仮想通貨の価格の線形回帰分析を行います。
筆者自身も調べながら書いていますので、この記事は常に更新の可能性があります。また、分かりにくいところがあればコメントしていただけると幸いです。
機械学習とは
さて、AIだのディープラーニングなど昨今でもてはやされていますが、そもそも機械学習とはなんなのでしょうか?
機械学習とは、経験からの学習により自動で改善するコンピューターアルゴリズムとその研究領域のことを指します。
元来、コンピュータにこなせる仕事は決定論的なものであり、予め分かっていることを素早く行わせることしかできませんでした。ですので、未知の現象に対して何かを判断させたり、予測を行うといったような仕事は苦手でした。
しかし、この機械学習の仕組みを取り入れることで、決定論的な枠組みの中でも、未知のものに対して判断を適用できたり、何かを予測したりするような仕事をこなすことができるようになります。具体的な例としては、
- 紙書類を電子化(画像認識)
- 農作物の生産量予測(データ予測)
- チャットボットによる問い合わせ対応(自然言語処理)
などが挙げられます。
次項からさっそくこの機械学習を簡単に扱えるscikit-learnとjupyter notebookを使っていきましょう。
環境構築
まず環境を作ります。
mkdir python_machine_learning # 適切な場所で作業用フォルダを作成
cd python_machine_learning # 移動
pipenv --python 3 # pythonの環境を初期化する
pipenv install scikit-learn numpy matplotlib # scikit-learn と関連パッケージをインストールする
pipenv install --dev jupyter # jupyterというグラフィカルな対話式実行環境をインストールする
code . # VScodeで開く
JupyterNotebookの起動
jupyter notebookの環境を開いてみましょう。
pipenv run jupyter notebook # jupyter notebookのサーバーを立ち上げる
するとURLが表示されるので、アクセスしてみてください。
ファイラーが開かれていればOKです。

Jupyter Notebookを使ってみる
jupyter notebookはGUIの対話式実行環境です。まず試しにファイルを作成しましょう。Python3を選択してください。
新規ファイルの作成
すると入力ブロックが現れるかと思います。

対話式実行環境が表示される
簡単に操作方法を書いておきます。
- [Ctrl + Enter]で実行可能
- [Shift + Enter]で新しい入力ブロック作成(Cellといいます)
- [D]キーを二度押すと削除
いくつか処理を実行してみてください。
ファイル名を変更しておきましょう。とりあえずtest
統計用語
この先に入る前に少し統計用語について書いておきます。既に知っている人は飛ばしてください。もし初めてこれらの式を見る方は、少し面食らうかもしれませんが、後述する課題のソースコードを読んで、式の意味を理解してみてください。
平均(Average)
データの値の合計をデータの総数で割った値。データ集合
偏差(Deviation)
各データの平均との差のこと。データ集合
分散(Variance)
各データの平均値からの偏差の自乗の平均の値。データの散らばり具合を表す。分散Vは平均
標準偏差(Standard Deviation)
分散に対する正の平方根。分散を人間にとって認識しやすい単位系に計算しなおしたもの。標準偏差Sは分散Vを用いて以下のように表される。
正規化(Normalize)
最大値から最小値までの範囲の数値を1-0の範囲にマッピングすること。正規化された各データ要素
標準化(Standardization)
データの平均を0に、分散を1にするようにデータを整形すること。
標準化された各データ要素の値
課題1 統計の式をPythonで書こう
次の気温の配列データtemp = [16.1,19.2,22.0,18.7,18.0,20.0,18.4]に対して、次の計算を行うPythonのソースコードを書いてください。また、結果についても記載してください。
- 平均値
- 偏差
- 分散
- 標準偏差
- 正規化
- 標準化
回答例
ave = sum(temp)/len(temp) # 18.914285714285715
print(ave)
dev = list(map(lambda x: x - ave, temp))
print(dev) # [-2.814285714285713, 0.2857142857142847, 3.0857142857142854, -0.2142857142857153, -0.9142857142857146, 1.0857142857142854, -0.514285714285716]
var = sum(map(lambda x: x**2, dev))/len(dev)
print(var) # 2.8355102040816313
import math
sd = math.sqrt(var)
print(sd) # 1.6838973258728192
normalized = list(map(lambda x:(x - min(temp))/(max(temp) - min(temp)), temp))
print(normalized) # [0.0, 0.525423728813559, 1.0, 0.4406779661016947, 0.3220338983050846, 0.6610169491525423, 0.3898305084745759]
standardization = list(map(lambda x:(x - ave)/sd, temp))
print(standardization) # [-1.6712929411102762, 0.16967441026500213, 1.8324836308620294, -0.12725580769875264, -0.5429581128480089, 0.6447627590070102, -0.30541393847700593]
scikit-learnについて
今回は機械学習を行うために、scikit-learnを使ってみようと思います。scikit-learnはpythonの機械学習ライブラリです。Scikit-learnを用いることで以下のような統計的処理を簡単に記述することができます。
- Classfication(分類)
- 対象がどのカテゴリーに属するかを判断する
- 迷惑メール判断、画像認識
- Regression(回帰)
- 対象に関連する連続値の値を予想する
- 薬の効果反応の予測、株価の予測
- Clustering(クラスタリング)
- 似た対象のグルーピングを自動化する
- 顧客区分け、実験結果のグルーピング
- Dimensionality reduction(次元削減)
- 確率変数を削減して簡略化する
- 可視化, 効率化
- Model Selection(モデル選択)
- モデルを比較検討し選択する
- 精度向上
- Preprocessing(前処理)
- 特徴抽出と正規化
- テキストのような入力データを機械学習で使えるようなデータに変換する、など
機械学習と一言にいっても、色々な応用例がありそうですね。それでは、サンプルを動かしてみて、scikit-learnの機能を大まかに見ていきましょう。
機械学習の基礎
まず、機械学習では大まかに次のような流れで検討を行います。
- モデルを決める(アルゴリズムを策定する)
- モデルに適用しやすいようにデータを加工する
- モデルにデータを学習させる
- モデルを使用する
- モデルの精度を確認する
scikit-learnには機械学習のためのアルゴリズムモデルがたくさん用意されていて、それらのことをestimator(推定器) といいます。
それぞれ推定器はデータをfit(学習)することができます。例として、RandomForestClassifier にシンプルなデータを学習させてみましょう。
ランダムフォレストは決定木を用いたアルゴリズムで、今回の例では分類タスクを行わせてみましょう。
ランダムフォレストについて大まかに把握したい方はこちらの記事をご覧ください。
JupyterNotebookを起動して、下記のスクリプトを打ち込んでみてください。
from sklearn.ensemble import RandomForestClassifier
clf = RandomForestClassifier(random_state=0)
X = [[ 1, 2, 3], # 2 サンプル, 特徴の数が3のデータ。
[11, 12, 13]]
y = [0, 1] # 教師データ。[1,2,3]のデータを0に、[11,12,13]のデータを1に対応付ける。
clf.fit(X, y)

ここで、fitの引数は以下のようなものになります。
- X: サンプルデータ。データは行:サンプル、列:属性データの行列になる。
- y: 回帰課題では実数,分類課題では整数。通常1次元の配列であり,n番目の値がXのn番目のサンプルの数値に対応する。
一度学習させた推定器は未知の値に対しても予測を行うことができます。
# トレーニングデータの分類を予測する
clf.predict(X) # => array([0, 1])
# 未知の値の分類予測
clf.predict([[4, 5, 6], [14, 15, 16]]) # => array([0, 1])
clf.predict([[14, 15, 16],[4, 5, 6]]) # =>array([1, 0])
clf.predict([[14, 15, 16],[7,8,9],[7,6,5],[4, 5, 6]]) # => array([1, 1, 0, 0])

データ整形と前処理
多くの機械学習ではデータを学習させる前に生データを扱いやすいように整形したり、なんらかの統計的処理として前処理を行います。scikit-learnではこれらの処理もとても扱いやすくなっています。
# StandardScalerはデータを標準化(各列の平均が0に、分散が1になるような数値の整形)する処理
# 平均は各データを足して要素数で割った数値
# 分散は各データの平均値との差を二乗し、平均をとったもの
from sklearn.preprocessing import StandardScaler
X = [[0, 15],
[1, -10]]
ss = StandardScaler().fit(X) # フィッティングさせる。
ss.transform(X) # => array([[-1., 1.],[ 1., -1.]]) # 訓練データを標準化したもの
Y = [[2,5],[4,-12]] # 未知データ
ss.transform(Y) # => array([[ 3. , 0.2 ],[ 7. , -1.16]])

パイプライン処理: 前処理と推定器を繋ぐ
前処理したデータを推定器に簡単につなぐことができます。
Piplineオブジェクトを用います。以下の例ではscikit-learnに搭載されているアヤメのデータを使って、訓練データとテストデータに分けて、piplineを使ってみましょう。
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import make_pipeline
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# pipelineオブジェクトを作成する
pipe = make_pipeline(
StandardScaler(), # 標準化用の前処理
LogisticRegression() # ロジスティック回帰の推定器
)
# アヤメのデータをロードして、トレーニングデータとテストデータに分ける
X, y = load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
# パイプラインを学習させる
pipe.fit(X_train, y_train)
その後、学習させた推定器を使って推定させた結果と、教師データを比べてどれぐらいあっているのかみてみましょう。
accuracy_score(pipe.predict(X_test), y_test)
# => 0.9736842105263158
0.97なので、97パーセントぐらいは正しい推定が出来ているようです。

モデル評価
前項のアヤメの例のように、予測の妥当性を確認する目的で学習データを訓練用データとテストデータに分けて、学習モデルの妥当性を評価する方法があり、これを交差検証(クロスバリデーション)と呼びます。
scikit-learnではこの交差検証を行う方法も簡単に扱えるよう用意されています。
例を見てみましょう。
from sklearn.datasets import make_regression
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_validate
# 回帰モデル用のデータを生成する この場合はサンプル数1000、random性を排除してデータを作る
X, y = make_regression(n_samples=1000, random_state=0)
lr = LinearRegression()
# デフォルトではデータを5分割してクロスバリデーションを行う。
# 詳しくはk-分割交差検証 ( https://ja.wikipedia.org/wiki/%E4%BA%A4%E5%B7%AE%E6%A4%9C%E8%A8%BC#k-%E5%88%86%E5%89%B2%E4%BA%A4%E5%B7%AE%E6%A4%9C%E8%A8%BC )
# を参照
result = cross_validate(lr, X, y)
result['test_score'] # => array([1., 1., 1., 1., 1.])
# データが簡単なので交差検証の妥当性が高い
自動パラメータ探索
すべての推定器には学習時に設定するパラメータがあり、これをハイパーパラメータと呼びます。例えば、特徴量の特徴抽出方法やモデルの種類を指します。
推定器の応用性はいくつかのパラメータに強く依存します。例えば、RandomForestRegressor には,森の中の木の数を決める n_estimators パラメータと,各木の最大深さを決める max_depth パラメータがあります。これらのパラメータは手元のデータに依存するため、正確な値が不明な場合が非常に多いです。
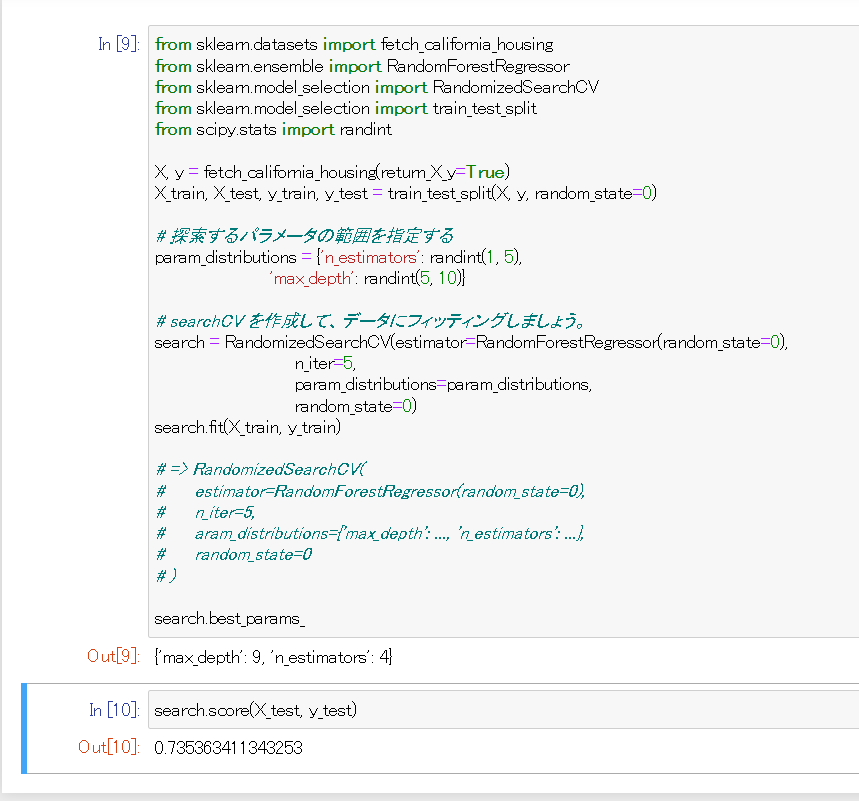
scikit-learnは最適なパラメータの組み合わせを自動的に見つけるツールを提供します。以下の例では、RandomizedSearchCV オブジェクトを用いて、ランダムフォレストのパラメータをランダムに探索します。探索が終わると,RandomizedSearchCV は最適なパラメータ・セットでフィッティングされた RandomForestRegressor として振る舞います。
from sklearn.datasets import fetch_california_housing
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import RandomizedSearchCV
from sklearn.model_selection import train_test_split
from scipy.stats import randint
X, y = fetch_california_housing(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
# 探索するパラメータの範囲を指定する
param_distributions = {'n_estimators': randint(1, 5),
'max_depth': randint(5, 10)}
# searchCV を作成して、データにフィッティングしましょう。
search = RandomizedSearchCV(estimator=RandomForestRegressor(random_state=0),
n_iter=5,
param_distributions=param_distributions,
random_state=0)
search.fit(X_train, y_train)
# => RandomizedSearchCV(
# estimator=RandomForestRegressor(random_state=0),
# n_iter=5,
# aram_distributions={'max_depth': ..., 'n_estimators': ...},
# random_state=0
# )
search.best_params_ # => {'max_depth': 9, 'n_estimators': 4}
# これで探索オブジェクトは norman random forest estimatorとして振る舞うようになった
# max_depth = 9, n_estimators=4
# テスト用データとその教師データにたいして適用する
search.score(X_test, y_test) # => 0.735363411343253
# 比較的高い精度であることがわかる
仮想通貨データの回帰分析
それではscikit-learnの基本機能をさらったところで、実際に使ってみることにしましょう。ここでは回帰分析のなかでも最も基本的な線形回帰分析を行いたいと思います。
線形回帰分析
線形回帰分析は、ある変数の値を、別の変数の値に基づいて予測するために使用されます。予測したい変数は、目的変数と呼ばれます。他の変数の値を予測するために使用する変数は、説明変数と呼ばれます。
この形式の分析では、目的変数の値を最適に予測する1つ以上の説明変数を使用して、線形方程式の係数が推定されます。線形回帰は、予測された出力値と実際の出力値との間の矛盾を最小限に抑える直線に適合します。式にすると、目的変数を
この係数
最小二乗法
scikit-learnのLinearRegressionは最小二乗法を使用して、最適な直線を生成します。その直線をもちいて、次に未知の説明変数データから未知の目的変数の値を推定します。
最小二乗法の例を下記の画像に上げます。最小二乗法では「各点と直線までの差の二乗の値が最小になるような直線」を導出します。
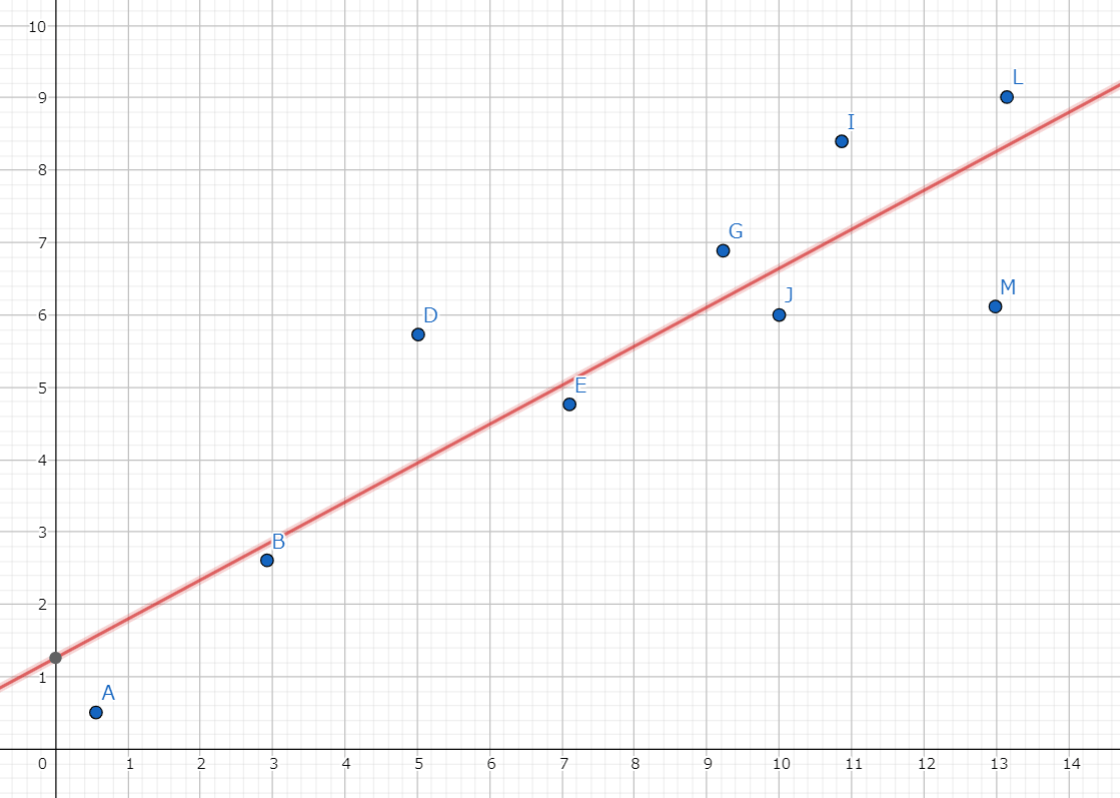
与えられたデータから算出された直線。
この直線は、「各点とその直線までの差の二乗」の値が最小になるような直線になっている。
統計上の特性から、この直線を
より詳しくはこちらが参考になると思います。
今回は、データ取得の容易さから仮想通貨の価格の変動に対して線形回帰分析を行ってみましょう。
目的変数は価格(Usd)で、説明変数は時間(Unix時間)となります。また、このような説明変数が1変数である線形回帰分析を、単回帰分析と呼びます。
新規ノートブックの作成
Jupyter Notebookのファイル画面から、新規作成を行ってください。ファイル名はなんでもいいですが、ここではcoin_regとしました。
為替データの取得
仮想通貨の情報を取得できるPublic Api( https://documenter.getpostman.com/view/5734027/RzZ6Hzr3#80653def-a398-4ccd-8101-f4a47856e767 )があるので、それを用いましょう。
今回はHTTPアクセスにpython標準ライブラリを用います。
import urllib.request # HTTPリクエストの標準ライブラリ
# 直近24時間のBitcoinの価格のチャートを取得する
url = "https://api.coinstats.app/public/v1/charts?period=24h&coinId=bitcoin"
response = urllib.request.urlopen(url)
response_utf8 = response.read().decode('utf-8')
print(response.getcode()) # httpステータス。200が帰ってきていたらアクセス成功。
print(response_utf8) # => 例:{"chart":[[1648104600,43148.9712,1,14.1248]......]}
# 帰ってくる配列
# BTC = Bitcoin、ETH = Ethereum、USD = アメリカドル
# [[unix_time(UNIX時間), BTC_to_USD(BTCのドル価格),BTC_to_BTC(BTCのBTC価格:1), BTC_to_ETH(BTCのETH価格)],....]

取得データの可視化
取得したデータは数字の羅列でイメージしにくいので、図示してみようと思います。
まずグラフ描画にはmatplotというパッケージを使います。
import numpy as np
json = eval(response_utf8) # 文字列をオブジェクトに変換
nary = np.array(json["chart"]) # numpyにより提供される配列(ndarray)に変換
print(nary)

二重配列データを取り出してndarrayに変換する
その後、散布図を描画します。
import matplotlib.pyplot as plt
x = nary[:,0] # ndarrayの二重配列は[:,列]の記法で列を取り出せる。unixtimeの列を取得
y = nary[:,1] # BTC/USDの列を取得
# 散布図を作成する
plt.scatter(x,y,5) # xの値, yの値, マーカーの大きさ
plt.plot(x,y)
# 散布図の各点を線で結ぶ
plt.show() # 表示する
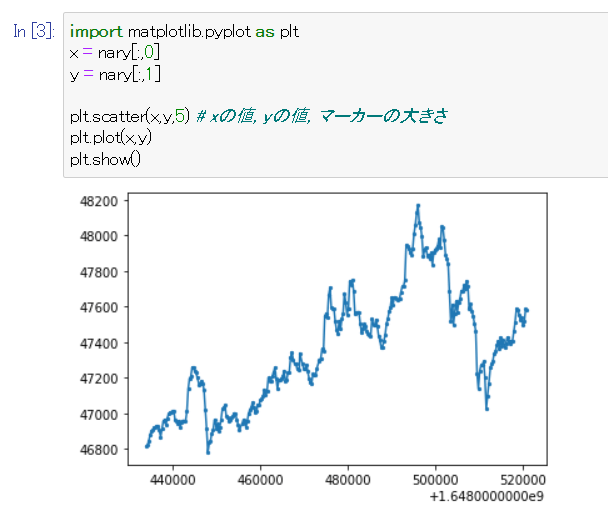
図示することでデータの概要が掴みやすくなる
回帰直線の取得
それでは次に、線形回帰分析を行い、最も適合する直線を求めてみましょう。
# sklearn.linear_model.LinearRegression クラスを読み込み
from sklearn import linear_model
lr = linear_model.LinearRegression()
X = x.reshape(-1,1) # 配列を縦のベクトルに変換する
Y = y.reshape(-1,1) # 配列を縦のベクトルに変換する
# 予測モデルを作成
lr.fit(X, Y)
# # 回帰係数
# Y = aX + bにおけるa
print(lr.coef_)
# # 切片
# Y = aX + bにおけるb
print(lr.intercept_)
# # 決定係数を表示する
## 説明変数が目的変数をどれくらい説明できるかを表す値。
print(lr.score(X, Y))
plt.scatter(x,y,5) # xの値, yの値, マーカーの大きさ
plt.plot(x,y)
plt.plot(X, lr.predict(X), color = 'red')
plt.show()
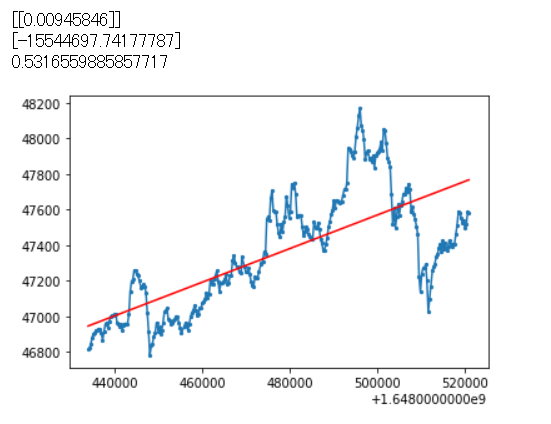
回帰直線を引くことができた
それでは作成した線形回帰モデルに、一日後の価格を予想させてみましょう。
import time
t = int(time.time()) # 現在時刻のunixtimeを取得する
print(t)
t = t + 86400 # 一日後の時間を求めるために86400秒足す
print(lr.predict([[t]]))
P = np.append(x, t).reshape(-1,1)
plt.scatter(x,y,5) # xの値, yの値, マーカーの大きさ
plt.plot(x,y)
plt.plot(P, lr.predict(P), color = 'green', linestyle="dashed") # 予測部分は破線で描画する
plt.plot(X, lr.predict(X), color = 'red')
plt.scatter([[t]], lr.predict([[t]]),100) # 一日後の価格予想点
plt.show()
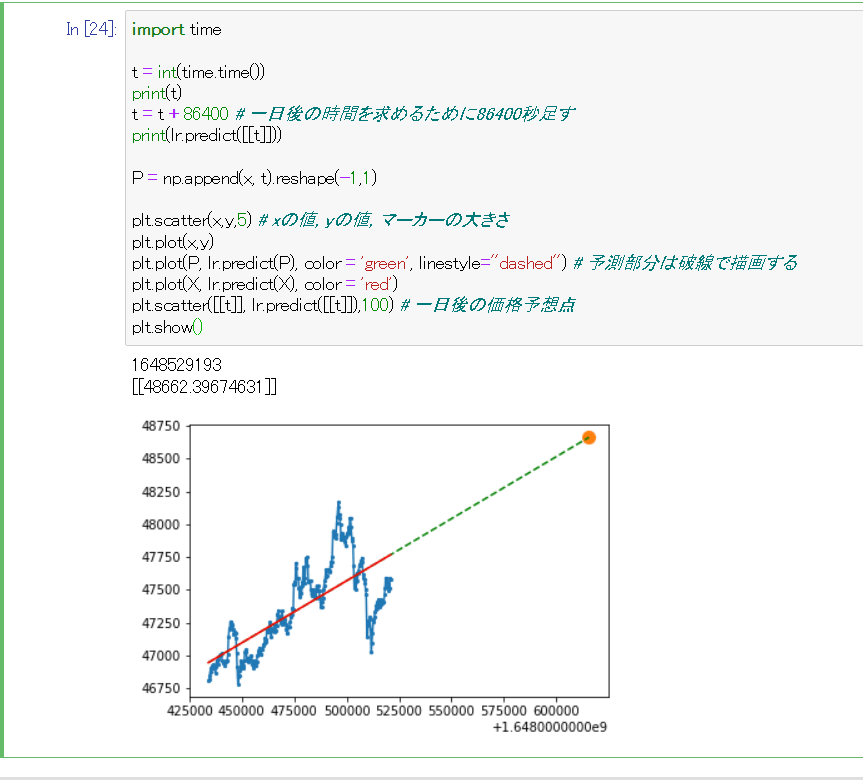
線形回帰分析を用いて1日後の価格を推定することができた
課題2 考察してみよう
今回の例ではscikit-learnを用いて単回帰分析を行いました。ここで振り返ってみましょう。
- 今回の例では仮想通貨の価格に対して回帰分析を行いましたが、この分析は信頼してよいでしょうか? 例えばこの分析に基づいて10年後の価格を推定した場合の値はどれぐらい正しいと言えるでしょうか? 考えを述べてください。
- より正しい推論を行うために、どのようなことをしたら良いか考えてみてください。
- 何かデータを取得し、回帰分析を行ってその結果とソースコードを提出してください。
回答例
あまり信頼してはいけません。仮想通貨の価格は過去の価格と時間のみを説明変数として従属する値ではないからです。仮想通貨の価格は需要と供給、政治的背景などによって大きな影響を受けます。
ちなみにだからと言って過去の価格履歴が全く影響がないかというとそういうわけでもありません。この辺りについては チャート分析とファンダメンタル分析 で調べると良いと思います。
- より多くの情報を元に推測する(多次元化)
- 線形単回帰分析よりももっと時系列データに適したモデルを導入する。
といった方法があります。
1990-2021の経済成長率と合計特殊出生率から線形回帰分析を行います。
import numpy as np
# GDP成長率
raw_gdp_growth = sorted({
"2019" :0.270308582079323,
"2018" :0.323207337906922,
"2017" :2.16829073737318,
"2016" :0.521944455486121,
"2015" :1.2229210410615,
"2014" :0.374719476350435,
"2013" :2.00026784118108,
"2012" :1.49508958593034,
"2011" :-0.115421339757418,
"2010" :4.19173925854747,
"2009" :-5.41641279666185,
"2008" :-1.09354060044625,
"2007" :1.65418388105051,
"2006" :1.42000655604306,
"2005" :1.662670405285,
"2004" :2.20468788221162,
"2003" :1.52822014817859,
"2002" :0.117992776889338,
"2001" :0.406335903187042,
"2000" :2.77963282512113,
"1999" :-0.251954272065987,
"1998" :-1.12840982877319,
"1997" :1.0760452342591,
"1996" :3.09999929079811,
"1995" :2.74214032190356,
"1994" :0.993066363346571,
"1993" :-0.517919847163228,
"1992" :0.848069581386284,
"1991" :3.41749676156724,
"1990" :4.89271306580787,
}.items())
gdp_growth = [t[1] for t in raw_gdp_growth]
# 合計特殊出生率
raw_total_fertility_rate = {
"1990": 1.54,
"1991": 1.53,
"1992": 1.50,
"1993": 1.46,
"1994": 1.50,
"1995": 1.42,
"1996": 1.43,
"1997": 1.39,
"1998": 1.38,
"1999": 1.34,
"2000": 1.36,
"2001": 1.33,
"2002": 1.32,
"2003": 1.29,
"2004": 1.29,
"2005": 1.26,
"2006": 1.32,
"2007": 1.34,
"2008": 1.37,
"2009": 1.37,
"2010": 1.39,
"2011": 1.39,
"2012": 1.41,
"2013": 1.43,
"2014": 1.42,
"2015": 1.45,
"2016": 1.44,
"2017": 1.43,
"2018": 1.42,
"2019": 1.36,
}.items()
total_fertility_rate = [t[1] for t in raw_total_fertility_rate]
# 二つの配列を二次元化する
data = np.array([list(e) for e in zip(gdp_growth, total_fertility_rate)])
print(data)
import matplotlib.pyplot as plt
x = data[:,0]
y = data[:,1]
from sklearn import linear_model
lr = linear_model.LinearRegression()
X = x.reshape(-1,1)
Y = y.reshape(-1,1)
# 予測モデルを作成
lr.fit(X, Y)
## 説明変数が目的変数をどれくらい説明できるかを表す値。
print(lr.score(X, Y))
# 0.06なのでこの回帰分析はあまり意味がないことが分かる
plt.scatter(x,y,5) # xの値, yの値, マーカーの大きさ
plt.plot(X, lr.predict(X), color = 'red')
plt.show()
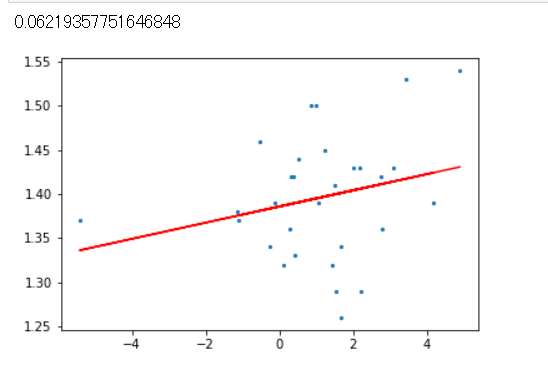
終わりに
今回の記事ではScikit-learnの機能をいくつかさらい、そのあと仮想通貨の価格の線形回帰分析を行いました。しかし、最後の課題で示したように、仮想通貨の価格を時間のみを説明変数として分析することはあまり良い分析モデルとは言えません。
次回の記事に、ARIMAモデルという時系列データに適したモデルを紹介する内容を予定しています。もしよろしければTwitterをフォローしてお待ちください。
Discussion