Zenn
⌛

Causal Forestで推定したCATEは、サブサンプル分析によるATEと一致するのか？

2024/11/12に公開
Python
計量経済学
rct
効果検証
tech

はじめに

前回の記事で、Causal Forestによる条件付き平均処置効果(CATE)のPythonによる推定方法を紹介しました。
https://zenn.dev/ka_ichi/articles/65a3dd6db5bb8f
この記事では、Causal Forestで推定した際の平均処置効果(ATE)の推定量が従来の方法で算出されるATEの推定量の値と近似することを示したうえで、shap値の違いからage(年齢)やeducation(教育年数)の違いがATEの異質性、すなわちCATEに貢献している可能性を示しました。

そこで今回は、Causal Forestによって算出されるCATEの推定量が、サブサンプル分析によって算出されるATEの推定量とどの程度一致するかを検証します。従来のRCTやA/Bテストでは、効果の異質性を明らかにするために、共変量の値によってサンプルを分割し、各サブサンプルごとにATEの推定量を算出し、その値を比較することが一般的です。そこで、これらの操作で算出されるATEの推定量は、Causal Forestによって算出されるCATEの推定量と一致するのか、あるいは相違があるのかを確かめ、相違があるとしたらそれはなぜなのかを考察することとします。
本記事はA/Bテストを行って効果の異質性を測ろうとする際に、Causal Forest(CausalForestDML)を使ってみようと思っている方にお勧めです。

この記事の要点【ネタバレ注意】

・Causal Forestによって推定できる 条件付き平均処置効果(CATE) と、共分散の値によるサブサンプル分析から得られる平均処置効果(ATE)とを比較しました。
・データは、教育訓練とその後の賃金に関するRCTデータで、教育年数を共変量としました。
・CATEにおいては、特定の年齢において、教育訓練がその後の賃金に有意に影響を与えることを示唆する結果を得ました。
・一方、年齢を20代、30代に区切ってサブサンプル分析を行うと、30代のサブサンプルにおいては1%有意水準において有意な結果を得た一方、20代のサブサンプルにおいては有意な結果を得ることができず、Causal Forestでの推定との結果のズレが生じました。
・この結果のズレに対して、サンプルサイズの問題を指摘しています。

パッケージとデータ

今回は、EcomMLというパッケージから、CausalForestDMLを使用します。Double Machine Learningに関しては、今回の紹介の管轄外として、こちらの記事を参照いただきたいと思います。
https://zenn.dev/s1ok69oo/articles/4da9e3b01a0a93#dmlの実装

また、今回使用するデータは、Lalonde(1986)で使用されている職業訓練に関するRCTデータです。このデータはNational Supported Work (NSW) Demonstrationという労働訓練プログラムのデータで、訓練の参加がランダムに振り分けられ、プログラム参加後の賃金に効果があるかを検証することができます。
https://users.nber.org/~rdehejia/nswdata2.html

Causal Forestの実行

セットアップ

import matplotlib.pyplot as plt
%matplotlib inline
import japanize_matplotlib
import pandas as pd
from sklift.models import SoloModel, ClassTransformation
import lightgbm as lgb
import seaborn as sns
import numpy as np
from sklearn.ensemble import RandomForestRegressor
from sklearn.ensemble import RandomForestClassifier
from econml.dml import CausalForestDML
import statsmodels.api as sm
from scipy.stats import norm

こちらでデータを取得します

df = pd.read_stata('https://users.nber.org/~rdehejia/data/nsw_dw.dta')

データの構造やATEの推定量の算出方法は、前回の記事をご参照ください。
https://zenn.dev/ka_ichi/articles/65a3dd6db5bb8f

Causal Forestの実装

CausalForestDMLを実装します。今回は、共変量のうち"age"を条件付けしたときの平均処置効果(CATE)の推定量を算出することを目指します。

X = df[['age']].values 
W = df[['married','nodegree','black','education']].values #X以外の共変量
T = df[['treat']].values #処置変数
Y = df['re78'].values 

#再現性のためにランダムシードを指定
random_seed = 42

#CausalForestDML推定器を設定
est = CausalForestDML(
    model_y=RandomForestRegressor(
        n_estimators=10, 
        min_samples_leaf=10, 
        random_state=random_seed 
    ),
    model_t=RandomForestClassifier(
        n_estimators=10, 
        min_samples_leaf=10, 
        random_state=random_seed 
    ),
    honest=True,  #HONEST法を使う
    discrete_treatment=True,
    n_estimators=100,  #木の数
    criterion='mse',  #評価指標
    max_depth=5,  #木の最大の深さ
    min_samples_split=10,  #ノードを分割するのに必要な最小限のサンプル数
    min_samples_leaf=5,  #各葉のノードに必要な最低限のサンプル数
    random_state=random_seed  
)

#モデルをフィット
est.fit(Y, T, X=X, W=W, cache_values=True)

est.summary(alpha=0.05)


このモデルを使って、ageの値で条件付けした際の平均処置効果、CATEを可視化すると、以下の通りとなる。

#CATEの推定
tau = est.effect(X)

#ATEの推定
ate = est.ate(X)  

# グラフの描画
plt.figure(figsize=(8, 6))
plt.title('CATE')
plt.scatter(X[:, 0], tau, label='CATE')  #CATEを散布図で表示
plt.axhline(y=ate, color='red', linestyle='--', label='ATE')  #ATEを赤い水平線で表示
plt.xlabel('age')
plt.ylabel('推定値')
plt.legend()
plt.show()


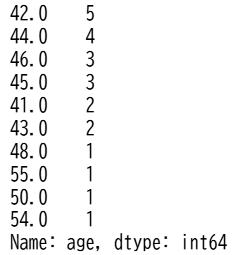
この結果は、対象者が25~40歳の場合、ATEよりも高い効果が生まれることを示唆しています。一方で、40歳を超えるとCATEの値が不自然に一定となっており、この区間においては効果が見られない、あるいはサンプルサイズが極端に小さい可能性があることが示唆されています。実際に、40歳以上のサンプルは以下のように少数であることが分かります。

df[df['age']>40]['age'].value_counts()

さて、本題に戻ります。ageで条件付けした際に、5%有意水準で有意であるCATEの推定量は、以下のように算出されます。

#'age'のユニークな値を取得
unique_ages = df['age'].unique()

#CATE、標準誤差、t値をユニークな'age'値に基づいて抽出
unique_results = []
for age in unique_ages:
    cate_value = cate_values[df['age'] == age][0]
    std_err = cate_std_err[df['age'] == age][0]
    t_value = cate_value / std_err
    
    unique_results.append({'age': age, 'cate': cate_value, 'std_err': std_err, 't_value': t_value})

#DataFrameに格納
unique_results_df = pd.DataFrame(unique_results)

#p値の計算とデータフレームに追加
unique_results_df['p_value'] = 2 * (1 - norm.cdf(np.abs(unique_results_df['t_value'])))

#p値が0.05未満の行のみ抽出
significant_results_df = unique_results_df[unique_results_df['p_value'] < 0.05]

#結果の表示
print(significant_results_df[['age', 'cate', 'std_err', 't_value', 'p_value']])


この結果から、22,26,27,32歳のCATEの推定量が5%有意水準で有意であることがわかります。また、これらの推定量は全体のATEの推定量よりも値が大きいことが分かります。

サブサンプル分析の実装

続いてageを層別に分け、サブサンプルごとにATEを推定し、効果の異質性を検証します。
ageは、20歳未満、20代、30代、40代、50代以上にわけ、そのうちサンプルサイズの観点から20歳未満、20代、30代のサブサンプルごとの効果を検証します。
サブサンプル作成は以下の通りです。

また、ぞれぞれのサブサンプルのサイズとtreatment割合は以下の通り算出されます。

#20歳未満サブサンプル
size_under20 = len(df_under_20)
print(f"under20のサンプルサイズ：{size_under20}")
t_percent_under20 = len(df_under_20[df_under_20['treat'] == 1]) / len(df_under_20)
print(f"under20のtreatmentの割合：{t_percent_under20}")

#20代サブサンプル
size_20 = len(df_20)
print(f"20'sのサンプルサイズ：{size_20}")
t_percent_20 = len(df_20[df_20['treat'] == 1]) / len(df_20)
print(f"20'sのtreatmentの割合：{t_percent_20}")

#30代サブサンプル
size_30 = len(df_30)
print(f"30'sのサンプルサイズ：{size_30}")
t_percent_30 = len(df_30[df_30['treat'] == 1]) / len(df_30)
print(f"30'sのtreatmentの割合：{t_percent_30}")

次に、各サブサンプルにおいてATEの推定量を算出します。コードと結果は以下の通りです。

#20歳未満サブサンプルのATE推定量算出
print(df_under_20[df_under_20['treat'] == 1]['re78'].mean() - df_under_20[df_under_20['treat'] == 0]['re78'].mean())
u_test_under_20 = stats.mannwhitneyu(df_under_20[df_under_20['treat'] == 1]['re78'], df_under_20[df_under_20['treat'] == 0]['re78'], alternative="two-sided")
#p値を出力
print(f"under20のATEのp値: {u_test_under_20.pvalue}")

#20代サブサンプルのATE推定量算出
print(df_20[df_20['treat'] == 1]['re78'].mean() - df_20[df_20['treat'] == 0]['re78'].mean())
u_test_20 = stats.mannwhitneyu(df_20[df_20['treat'] == 1]['re78'], df_20[df_20['treat'] == 0]['re78'], alternative="two-sided")

print(f"20'sのATEのp値: {u_test_20.pvalue}")

#30代サブサンプルのATE推定量算出
print(df_30[df_30['treat'] == 1]['re78'].mean() - df_30[df_30['treat'] == 0]['re78'].mean())
u_test_30 = stats.mannwhitneyu(df_30[df_30['treat'] == 1]['re78'], df_30[df_30['treat'] == 0]['re78'], alternative="two-sided")
print(f"30'sのATEのp値: {u_test_30.pvalue}")

この結果から、30代サブサンプルにおいては1%有意水準で有意な結果を得ました。フルサンプルのATE推定量との比較から、30代における教育訓練の効果は約4000と、特に高いことが分かります。
一方で、20歳未満サブサンプルや20代サブサンプルにおいては、5%有意水準において有意な結果が得られませんでした。

考察

今回の検証では、CausalForestDMLを用いた推定とサブサンプル分析とを比較し、その結果がどの程度一致するかを比較しました。結果として、前者では22歳、26歳、27歳において有意な結果を得た一方、後者では20代のサブサンプルにおいては有意な結果を得ることができないなど、結果にずれが生じました。また、サブサンプルでは30代のサンプルにおいて有意な結果が出たものの、Causal Forestでは30代のうち有意な結果が得られたのは32歳のみでした。さらに、サブサンプル分析で得られた30代における効果の推定量の値の大きさは、Causal Forestで得られたCATEの推定量の値よりも大きいことが見て取れます。

こうした結果のズレの原因として、サンプルサイズが大きさにあると考察します。今回サブサンプル分析で有意な結果が得られた30代サブサンプルのサンプルサイズは65であり、個別の年齢ごとのサンプルサイズがかなり小さいことが分かります。このとき、CATEを推定しようとしてもサンプルサイズの問題から有効な推定ができなかったのでは、と判断できます。このように、CATEをCausal Forestで推定する際には、条件付けする共変量の値ごとのサンプルサイズが十分存在するかを確認することが大事であると考察します。

また、当たり前ですが、発生したズレの一部は、推定方法の違いによって説明できるものもあるのではと考えます。線形モデルを用いているサブサンプル分析と比べて、決定木モデルによるノンパラな推定を行っているCausal Forestの方が、特定の年齢での有意な効果を見つけやすいのでは、と推測することができます。ただし、これらは推測の域を超えないことを明記しておきます。

最後に、今回はageを連続変数のまま使用しましたが、サブサンプル分析と同じように20歳未満、20代、30代などと層化してみると近似した結果が出るのかどうか、疑問が生じたので、別の記事等で今後追加で検証してみたいと思います。

参考文献

Discussion